专题三十二 二次函数与等角的处理策略(含解析)
文档属性
| 名称 | 专题三十二 二次函数与等角的处理策略(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 193.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-04 07:07:38 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专题三十二 二次函数与等角的处理策略
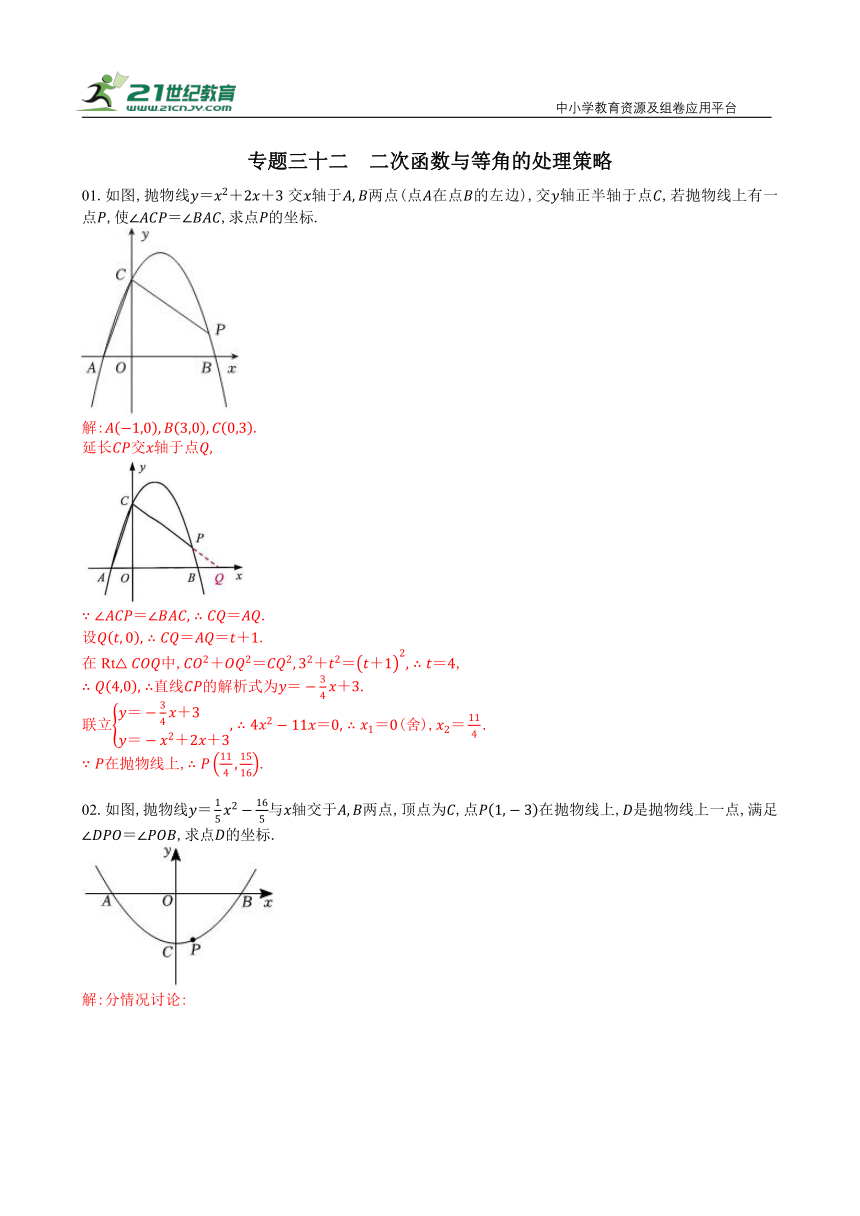
01.如图,抛物线交轴于两点(点在点的左边),交轴正半轴于点,若抛物线上有一点,使,求点的坐标.
02.如图,抛物线与轴交于两点,顶点为,点在抛物线上,是抛物线上一点,满足,求点的坐标.
03.如图,抛物线y=x2-x-2与x轴交于A,B两点,与y轴交于点C,在第四象限的抛物线上求点P,使∠PCB=∠CAB,求出点P的坐标.
专题三十二 二次函数与等角的处理策略
01.如图,抛物线交轴于两点(点在点的左边),交轴正半轴于点,若抛物线上有一点,使,求点的坐标.
解:.
延长交轴于点
.
设.
在Rt中,,
直线的解析式为.
联立(舍),
在抛物线上,.
02.如图,抛物线与轴交于两点,顶点为,点在抛物线上,是抛物线上一点,满足,求点的坐标.
解:分情况讨论:
(i)若,则关于轴对称,.
(ii)若在轴右侧,延长交轴于点,
.
设,作轴于,
.
而,,联立,得,
(舍)或.
03. 如图,抛物线y=x2-x-2与x轴交于A,B两点,与y轴交于点C,在第四象限的抛物线上求点P,使∠PCB=∠CAB,求出点P的坐标.
解:对于y=x2-x-2,令x=0,则y=-2,
∴C(0,-2),
令y=0,即x2-x-2=0,解得x=-1或x=2,
∴A(-1,0),B(2,0);
如图,延长PC交x轴负半轴于点H,过点A作AG⊥AC交CH于点G,过点G作GK⊥x轴于点K.
∵∠CAB+∠ABC+∠ACB=180°,∠PCB+∠ACG+∠ACB=180°
又∵∠CAB=∠PCB,
∴∠ACG=∠ABC=45°,
∴∠ABC=∠AGC=45°,
∴AG=AC,
又∠GAK+∠OAC=∠OAC+∠ACO=90°,
∴∠GAK=∠ACO,
∴△GKA≌△AOC(AAS),
∴AK=OC=2,KG=OA=1,
∴OK=3,
∴G(-3,-1),
∵点G(-3,-1),C(0,-2),
∴直线CG的解析式为yx-2,
联立,解得:(不合题意的值已舍去),
∴P(,).
专题三十二 二次函数与等角的处理策略
01.如图,抛物线交轴于两点(点在点的左边),交轴正半轴于点,若抛物线上有一点,使,求点的坐标.
02.如图,抛物线与轴交于两点,顶点为,点在抛物线上,是抛物线上一点,满足,求点的坐标.
03.如图,抛物线y=x2-x-2与x轴交于A,B两点,与y轴交于点C,在第四象限的抛物线上求点P,使∠PCB=∠CAB,求出点P的坐标.
专题三十二 二次函数与等角的处理策略
01.如图,抛物线交轴于两点(点在点的左边),交轴正半轴于点,若抛物线上有一点,使,求点的坐标.
解:.
延长交轴于点
.
设.
在Rt中,,
直线的解析式为.
联立(舍),
在抛物线上,.
02.如图,抛物线与轴交于两点,顶点为,点在抛物线上,是抛物线上一点,满足,求点的坐标.
解:分情况讨论:
(i)若,则关于轴对称,.
(ii)若在轴右侧,延长交轴于点,
.
设,作轴于,
.
而,,联立,得,
(舍)或.
03. 如图,抛物线y=x2-x-2与x轴交于A,B两点,与y轴交于点C,在第四象限的抛物线上求点P,使∠PCB=∠CAB,求出点P的坐标.
解:对于y=x2-x-2,令x=0,则y=-2,
∴C(0,-2),
令y=0,即x2-x-2=0,解得x=-1或x=2,
∴A(-1,0),B(2,0);
如图,延长PC交x轴负半轴于点H,过点A作AG⊥AC交CH于点G,过点G作GK⊥x轴于点K.
∵∠CAB+∠ABC+∠ACB=180°,∠PCB+∠ACG+∠ACB=180°
又∵∠CAB=∠PCB,
∴∠ACG=∠ABC=45°,
∴∠ABC=∠AGC=45°,
∴AG=AC,
又∠GAK+∠OAC=∠OAC+∠ACO=90°,
∴∠GAK=∠ACO,
∴△GKA≌△AOC(AAS),
∴AK=OC=2,KG=OA=1,
∴OK=3,
∴G(-3,-1),
∵点G(-3,-1),C(0,-2),
∴直线CG的解析式为yx-2,
联立,解得:(不合题意的值已舍去),
∴P(,).
同课章节目录
