专题三十七 二次函数与平行四边形(含解析)
文档属性
| 名称 | 专题三十七 二次函数与平行四边形(含解析) | 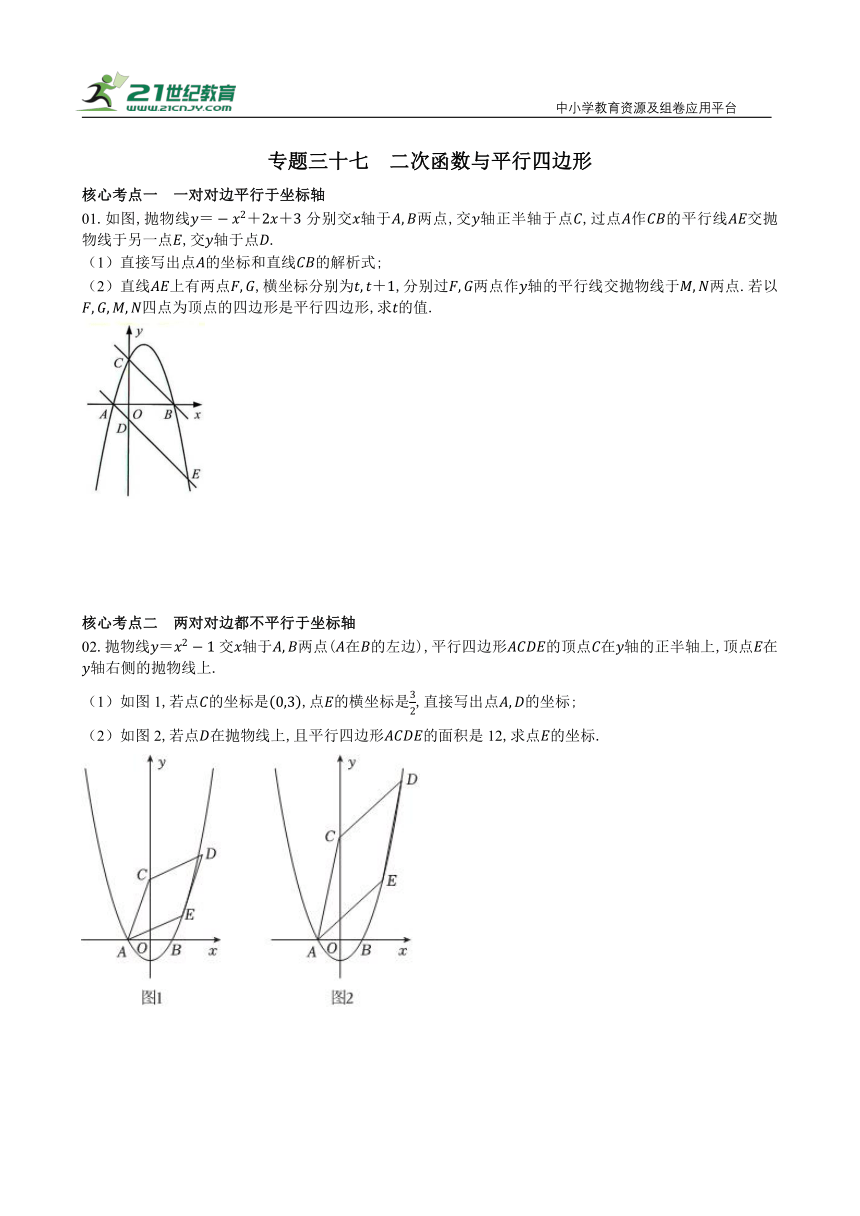 | |
| 格式 | docx | ||
| 文件大小 | 155.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-04 07:12:44 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专题三十七 二次函数与平行四边形
核心考点一 一对对边平行于坐标轴
01.如图,抛物线分别交轴于两点,交轴正半轴于点,过点作的平行线交抛物线于另一点,交轴于点.
(1)直接写出点的坐标和直线的解析式;
(2)直线上有两点,横坐标分别为,分别过两点作轴的平行线交抛物线于两点.若以四点为顶点的四边形是平行四边形,求的值.
核心考点二 两对对边都不平行于坐标轴
02.抛物线交轴于两点(在的左边),平行四边形的顶点在轴的正半轴上,顶点在轴右侧的抛物线上.
(1)如图1,若点的坐标是,点的横坐标是,直接写出点的坐标;
(2)如图2,若点在抛物线上,且平行四边形的面积是12,求点的坐标.
专题三十七 二次函数与平行四边形
核心考点一 一对对边平行于坐标轴
01.如图,抛物线分别交轴于两点,交轴正半轴于点,过点作的平行线交抛物线于另一点,交轴于点.
(1)直接写出点的坐标和直线的解析式;
(2)直线上有两点,横坐标分别为,分别过两点作轴的平行线交抛物线于两点.若以四点为顶点的四边形是平行四边形,求的值.
解:(1)点的坐标为,直线的解析式是.
(2),设的解析式为,
将点的坐标代入,得,解得,
的解析式为.
点在直线上,,
点,点,
.
以为顶点的四边形是平行四边形,
,即,解得或.
核心考点二 两对对边都不平行于坐标轴
02.抛物线交轴于两点(在的左边),平行四边形的顶点在轴的正半轴上,顶点在轴右侧的抛物线上.
(1)如图1,若点的坐标是,点的横坐标是,直接写出点的坐标;
(2)如图2,若点在抛物线上,且平行四边形的面积是12,求点的坐标.
解:(1)令,
,
四边形是平行四边形,由平移得.
(2)设点坐标为,点坐标为.
四边形是平行四边形,,
,点坐标为.
点在抛物线上,,
解得.
连,过点作轴垂线,垂足为,过点作,垂足为,
则,
,
,解得(不合题意,舍去),点的坐标是.
专题三十七 二次函数与平行四边形
核心考点一 一对对边平行于坐标轴
01.如图,抛物线分别交轴于两点,交轴正半轴于点,过点作的平行线交抛物线于另一点,交轴于点.
(1)直接写出点的坐标和直线的解析式;
(2)直线上有两点,横坐标分别为,分别过两点作轴的平行线交抛物线于两点.若以四点为顶点的四边形是平行四边形,求的值.
核心考点二 两对对边都不平行于坐标轴
02.抛物线交轴于两点(在的左边),平行四边形的顶点在轴的正半轴上,顶点在轴右侧的抛物线上.
(1)如图1,若点的坐标是,点的横坐标是,直接写出点的坐标;
(2)如图2,若点在抛物线上,且平行四边形的面积是12,求点的坐标.
专题三十七 二次函数与平行四边形
核心考点一 一对对边平行于坐标轴
01.如图,抛物线分别交轴于两点,交轴正半轴于点,过点作的平行线交抛物线于另一点,交轴于点.
(1)直接写出点的坐标和直线的解析式;
(2)直线上有两点,横坐标分别为,分别过两点作轴的平行线交抛物线于两点.若以四点为顶点的四边形是平行四边形,求的值.
解:(1)点的坐标为,直线的解析式是.
(2),设的解析式为,
将点的坐标代入,得,解得,
的解析式为.
点在直线上,,
点,点,
.
以为顶点的四边形是平行四边形,
,即,解得或.
核心考点二 两对对边都不平行于坐标轴
02.抛物线交轴于两点(在的左边),平行四边形的顶点在轴的正半轴上,顶点在轴右侧的抛物线上.
(1)如图1,若点的坐标是,点的横坐标是,直接写出点的坐标;
(2)如图2,若点在抛物线上,且平行四边形的面积是12,求点的坐标.
解:(1)令,
,
四边形是平行四边形,由平移得.
(2)设点坐标为,点坐标为.
四边形是平行四边形,,
,点坐标为.
点在抛物线上,,
解得.
连,过点作轴垂线,垂足为,过点作,垂足为,
则,
,
,解得(不合题意,舍去),点的坐标是.
同课章节目录
