专题四十一 二次函数与参数计算 (2) 一证明位置关系(含解析)
文档属性
| 名称 | 专题四十一 二次函数与参数计算 (2) 一证明位置关系(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 182.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-04 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专题四十一 二次函数与参数计算(2)一证明位置关系
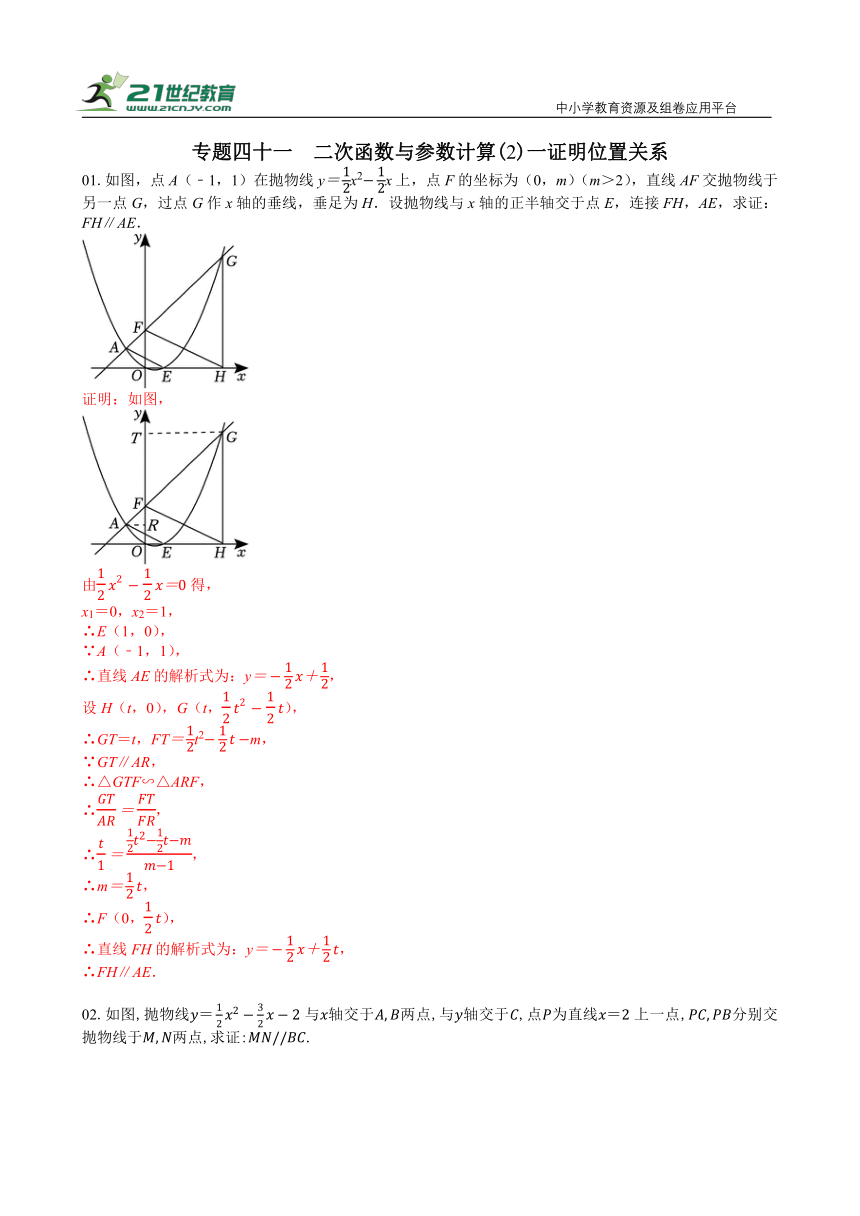
01.如图,点A(﹣1,1)在抛物线yx2x上,点F的坐标为(0,m)(m>2),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H.设抛物线与x轴的正半轴交于点E,连接FH,AE,求证:FH∥AE.
02.如图,抛物线与轴交于两点,与轴交于,点为直线上一点,分别交抛物线于两点,求证:.
03. 如图,过点F(0,)的直线交抛物线y=x2于S,T两点,直线PS,PT与抛物线均只有一个公共点,求证:PF⊥ST.
专题四十一 二次函数与参数计算(2)一证明位置关系
01.如图,点A(﹣1,1)在抛物线yx2x上,点F的坐标为(0,m)(m>2),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H.设抛物线与x轴的正半轴交于点E,连接FH,AE,求证:FH∥AE.
证明:如图,
由得,
x1=0,x2=1,
∴E(1,0),
∵A(﹣1,1),
∴直线AE的解析式为:y,
设H(t,0),G(t,),
∴GT=t,FTt2m,
∵GT∥AR,
∴△GTF∽△ARF,
∴,
∴,
∴m,
∴F(0,),
∴直线FH的解析式为:y,
∴FH∥AE.
02.如图,抛物线与轴交于两点,与轴交于,点为直线上一点,分别交抛物线于两点,求证:.
解:①,点设点的坐标为,
设,则,解得,
②,同理③
联立①②并整理得:,解得或(舍去),
即点,同理联立①③解得:或(舍去),
坐标为,直线的,直线的,故.
03. 如图,过点F(0,)的直线交抛物线y=x2于S,T两点,直线PS,PT与抛物线均只有一个公共点,求证:PF⊥ST.
证明:由题意,设S(s,s2),T(t,t2),则kSTs+t.
∴直线ST的解析式为:y=(s+t)(x﹣s)+s2=(s+t)x﹣st.
将F(0,)代入上式得,﹣st,
∴st.
设SP解析式为y=kx+b',
联立x2﹣kx﹣b'=0,
∴xs+xs=﹣(﹣k).
∴2xs=k.
∴SP的解析式为:y=2sx+b'.
代入(s,s2)得2s2+b'=s2,
∴b'=s2﹣2s2=﹣s2.
∴直线SP为:y=2sx﹣s2.
同理可得:直线PT:y=2tx﹣t2,
联立:,∴.
∴P(,st)即P(,).
∴PF2+SF2(s+t)2(s﹣0)2+(s2)2
s2t2st+s2+s4s2
=(t)2+(s2)2,
又PS2=(s)2+(s2﹣st)2=()2+(s2)2,
∴PF2+SF2=PS2.
∴PF⊥FS,即PF⊥ST.
专题四十一 二次函数与参数计算(2)一证明位置关系
01.如图,点A(﹣1,1)在抛物线yx2x上,点F的坐标为(0,m)(m>2),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H.设抛物线与x轴的正半轴交于点E,连接FH,AE,求证:FH∥AE.
02.如图,抛物线与轴交于两点,与轴交于,点为直线上一点,分别交抛物线于两点,求证:.
03. 如图,过点F(0,)的直线交抛物线y=x2于S,T两点,直线PS,PT与抛物线均只有一个公共点,求证:PF⊥ST.
专题四十一 二次函数与参数计算(2)一证明位置关系
01.如图,点A(﹣1,1)在抛物线yx2x上,点F的坐标为(0,m)(m>2),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H.设抛物线与x轴的正半轴交于点E,连接FH,AE,求证:FH∥AE.
证明:如图,
由得,
x1=0,x2=1,
∴E(1,0),
∵A(﹣1,1),
∴直线AE的解析式为:y,
设H(t,0),G(t,),
∴GT=t,FTt2m,
∵GT∥AR,
∴△GTF∽△ARF,
∴,
∴,
∴m,
∴F(0,),
∴直线FH的解析式为:y,
∴FH∥AE.
02.如图,抛物线与轴交于两点,与轴交于,点为直线上一点,分别交抛物线于两点,求证:.
解:①,点设点的坐标为,
设,则,解得,
②,同理③
联立①②并整理得:,解得或(舍去),
即点,同理联立①③解得:或(舍去),
坐标为,直线的,直线的,故.
03. 如图,过点F(0,)的直线交抛物线y=x2于S,T两点,直线PS,PT与抛物线均只有一个公共点,求证:PF⊥ST.
证明:由题意,设S(s,s2),T(t,t2),则kSTs+t.
∴直线ST的解析式为:y=(s+t)(x﹣s)+s2=(s+t)x﹣st.
将F(0,)代入上式得,﹣st,
∴st.
设SP解析式为y=kx+b',
联立x2﹣kx﹣b'=0,
∴xs+xs=﹣(﹣k).
∴2xs=k.
∴SP的解析式为:y=2sx+b'.
代入(s,s2)得2s2+b'=s2,
∴b'=s2﹣2s2=﹣s2.
∴直线SP为:y=2sx﹣s2.
同理可得:直线PT:y=2tx﹣t2,
联立:,∴.
∴P(,st)即P(,).
∴PF2+SF2(s+t)2(s﹣0)2+(s2)2
s2t2st+s2+s4s2
=(t)2+(s2)2,
又PS2=(s)2+(s2﹣st)2=()2+(s2)2,
∴PF2+SF2=PS2.
∴PF⊥FS,即PF⊥ST.
同课章节目录
