苏科版九年级数学下册试题 7.1 正切同步练习(含详解)
文档属性
| 名称 | 苏科版九年级数学下册试题 7.1 正切同步练习(含详解) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-04 10:33:50 | ||
图片预览



文档简介
7.1 正切
一.单选题
1.在中,,,,则的值为
A. B. C. D.
2.已知为锐角,且,则的取值范围是
A. B. C. D.
3.如图,的顶点在正方形网格的格点上,则的值为
A. B.1 C. D.
4.如图,4个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点,已知菱形的一个内角为,、、都是格点,则
A. B. C. D.
5.如图,在矩形中,点在上,将矩形沿折叠,使点落在边上的点处.若,,则的值为
A. B. C. D.
二.填空题
6.在中,,,则 .
7.如图,,,是小正方形的顶点,且每个小正方形的边长均为1,则的值为 .
8.如图,点在线段上,且,分别以、为边在线段的同侧作正方形、,连接、,则 .
9.如图,的顶点在正方形网格的格点上,则的值为 .
10.如图,中;,,将绕点顺时针方向旋转角得到△,连接,,面积为,则的面积等于 .
11.如图,半径为3的经过原点和点,点是轴左侧优弧上一点,则 .
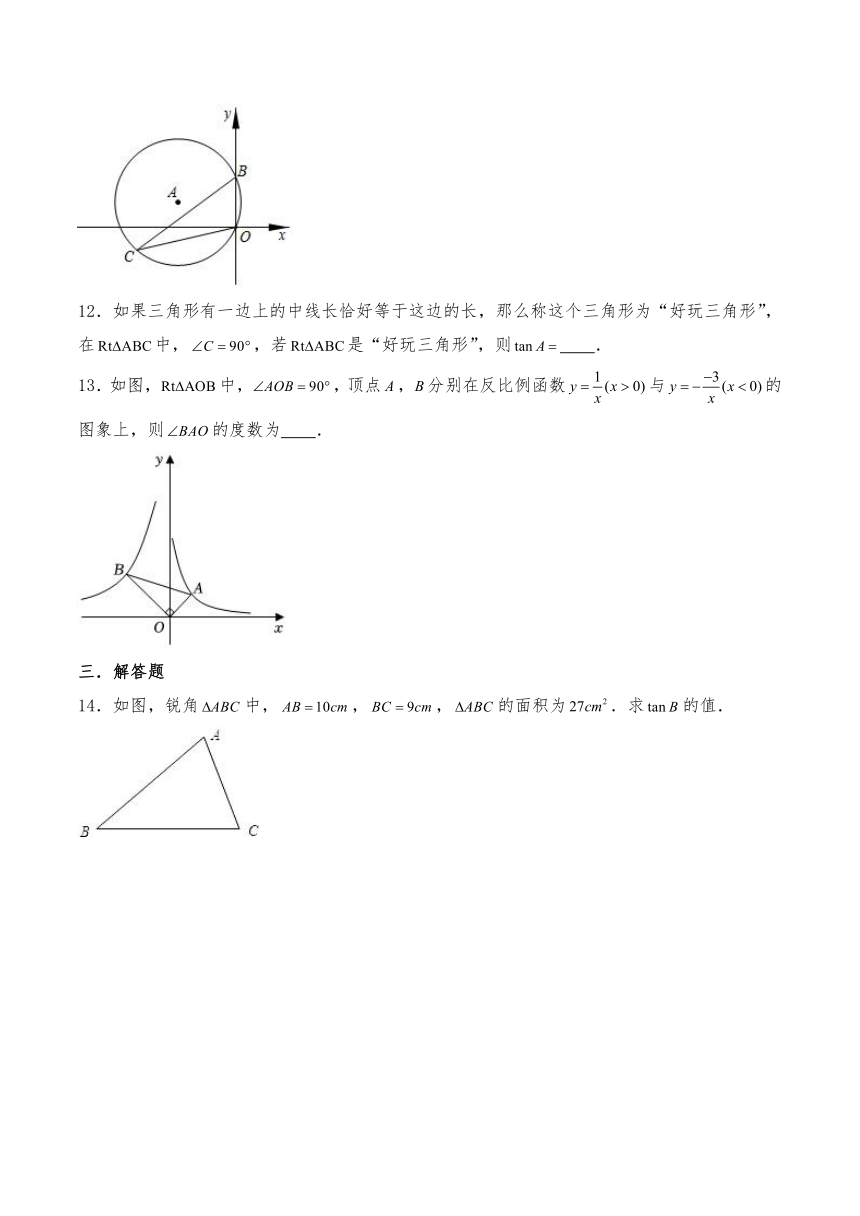
12.如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”,在中,,若是“好玩三角形”,则 .
13.如图,中,,顶点,分别在反比例函数与的图象上,则的度数为 .
三.解答题
14.如图,锐角中,,,的面积为.求的值.
15.如图, 在中,,已知,
(1) 如果,求;
(2) 如果,求.
16.如图,内接于圆,若圆的半径是,,求的值.
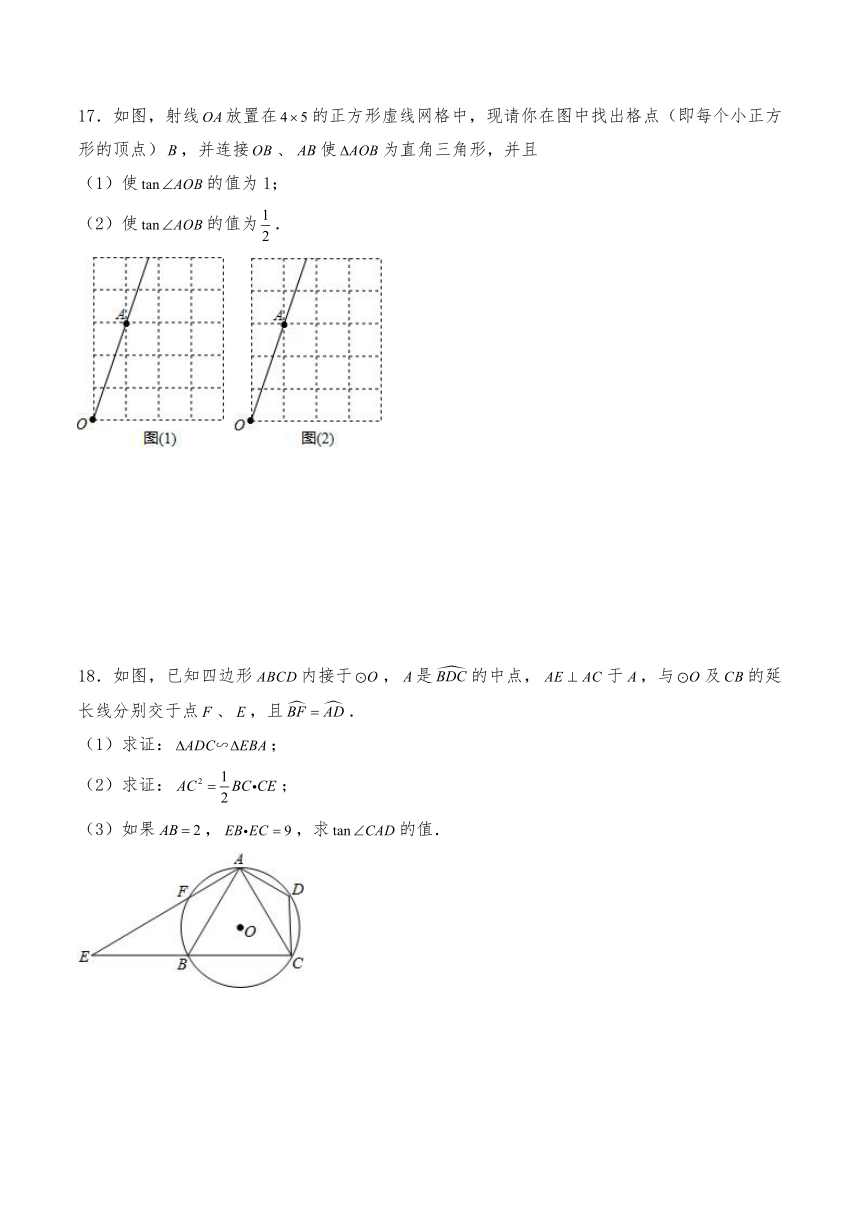
17.如图,射线放置在的正方形虚线网格中,现请你在图中找出格点(即每个小正方形的顶点),并连接、使为直角三角形,并且
(1)使的值为1;
(2)使的值为.
18.如图,已知四边形内接于,是的中点,于,与及的延长线分别交于点、,且.
(1)求证:;
(2)求证:;
(3)如果,,求的值.
19.如图,在正方形网格中,每个小正方形的边长均为1,线段和的端点都在网格线的交点上.若与相交于点,求的值.
20.在学习《解直角三角形》一章时,小华同学对一个角的倍角的三角函数值是否具有关系产生了浓厚的兴趣,进行了一般研究.
(1)初步尝试:我们知道: , ,发现结论: (填“”或“”
(2)实践探究:在解决“如图1,在中,,,,求的值”这一问题时,小华想构造包含的直角三角形,延长到,使,连接,所以得,即转化为求的正切值,请按小华的思路求的值;
(3)拓展延伸:如图2,在中,,,.请模仿小华的思路或者用你的新思路,试着求一求:①的值;②的值.
答案
一.单选题
1.
【详解】解:在中,,,,
由勾股定理得,,
则.
故本题选:.
2.
【详解】解:,,,
,
,
又一个锐角的正切值随锐角度数的增大而增大,
.
故本题选:.
3.
【详解】解:如图,延长交网格于点,连接,由网格以及正方形的性质可得,
由网格构造直角三角形可得,,,
在中,.
故本题选:.
4.
【详解】解:如图,连接,交于点,
由题意可得:,,
设,则,
故,
则.
故本题选:.
5.
【详解】解:四边形为矩形,
,,
矩形沿直线折叠,顶点恰好落在边上的处,
,,
在中,,
,
设,则,
在中,,
,解得,
.
故本题选:.
二.填空题
6.
【详解】解:如图,作于点,
则.
,
.
故本题答案为:.
7.
【详解】解:如图,连接,
由网格可得:,,
,
为等腰直角三角形,
,
则.
故本题答案为:1.
8.
【详解】解:如图,连接,
在正方形、中,
,
,
,
设,,
,,
.
故本题答案为:.
9.
【详解】解:如图,记垂足为D,
由格点知:,
.
,
,
,
.
.
.
10.
【详解】解:由旋转的性质可知,,
,
,,
,
,
,
,
,
.
面积为,
.
故本题答案为:8.
11.
【详解】解:如图,设交轴于,连接,则是直径,
在中,,,
则,
,
由圆周角定理得:,
则.
故本题答案为:.
12.
【详解】解:分两种情况:
①如图1,是边上的中线,,
设,则,
在中,,
,
;
②如图2,是边上的中线,,
设,则,
在中,,
,
,
,
,
综上,所求值为或.
故本题答案为或.
13.
【详解】解:如图,过作轴于点,过作轴于,
则,
顶点,分别在反比例函数与的图象上,
,,
,
,
,
,
,
,
,
,
故本题答案为:.
三.解答题
14.解:如图,过点作于,
,
,
,
,
,
.
15.解: (1),,
,,
在中,,
,又,
则;
(2) 在中,,
设,则,又,
利用勾股定理得:,
解得:或(舍 去) ,
则.
16.解:如图,作直径,连接,
和都对弧,
,
圆的半径是,
,
为直径,
,
,
.
17.解:(1)如图1所示:
(2)如图2所示.
18.(1)证明:四边形内接于,
.
,
,
;
(2)证明:如图,过作于,
是的中点,
,
又于,
,
,
,
,
,
,即,
又,
;
(3)解:是中点,,
,
①,
,
②,
联立①②得:,
,
,
,
,
,
.
19.解法一:如图,设与交于点,
,,
是的中位线,
,,
,
.
,
设,则,
,解得:,
,
,
,
在中,,
.
解法二:如图,
取格点,连接,,
,,
四边形为平行四边形,
,
,
,
,
,
,
为直角三角形,
.
20.解:(1),,
发现结论:,
故本题答案为:,,;
(2)在中,,,,
,
如图,延长至,使得,
,
,
,,
;
(3)①如图,作的垂直平分线交于,连接,
则,,,
中,,,,
,,
设,则,
在中,,
解得:,即,,
;
②如图,作交于点,使,
则.
设,则,
,
,即,
,
在中,,
即,
整理得:,
解得:,(不合题意,舍去),
即,,
.
一.单选题
1.在中,,,,则的值为
A. B. C. D.
2.已知为锐角,且,则的取值范围是
A. B. C. D.
3.如图,的顶点在正方形网格的格点上,则的值为
A. B.1 C. D.
4.如图,4个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点,已知菱形的一个内角为,、、都是格点,则
A. B. C. D.
5.如图,在矩形中,点在上,将矩形沿折叠,使点落在边上的点处.若,,则的值为
A. B. C. D.
二.填空题
6.在中,,,则 .
7.如图,,,是小正方形的顶点,且每个小正方形的边长均为1,则的值为 .
8.如图,点在线段上,且,分别以、为边在线段的同侧作正方形、,连接、,则 .
9.如图,的顶点在正方形网格的格点上,则的值为 .
10.如图,中;,,将绕点顺时针方向旋转角得到△,连接,,面积为,则的面积等于 .
11.如图,半径为3的经过原点和点,点是轴左侧优弧上一点,则 .
12.如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”,在中,,若是“好玩三角形”,则 .
13.如图,中,,顶点,分别在反比例函数与的图象上,则的度数为 .
三.解答题
14.如图,锐角中,,,的面积为.求的值.
15.如图, 在中,,已知,
(1) 如果,求;
(2) 如果,求.
16.如图,内接于圆,若圆的半径是,,求的值.
17.如图,射线放置在的正方形虚线网格中,现请你在图中找出格点(即每个小正方形的顶点),并连接、使为直角三角形,并且
(1)使的值为1;
(2)使的值为.
18.如图,已知四边形内接于,是的中点,于,与及的延长线分别交于点、,且.
(1)求证:;
(2)求证:;
(3)如果,,求的值.
19.如图,在正方形网格中,每个小正方形的边长均为1,线段和的端点都在网格线的交点上.若与相交于点,求的值.
20.在学习《解直角三角形》一章时,小华同学对一个角的倍角的三角函数值是否具有关系产生了浓厚的兴趣,进行了一般研究.
(1)初步尝试:我们知道: , ,发现结论: (填“”或“”
(2)实践探究:在解决“如图1,在中,,,,求的值”这一问题时,小华想构造包含的直角三角形,延长到,使,连接,所以得,即转化为求的正切值,请按小华的思路求的值;
(3)拓展延伸:如图2,在中,,,.请模仿小华的思路或者用你的新思路,试着求一求:①的值;②的值.
答案
一.单选题
1.
【详解】解:在中,,,,
由勾股定理得,,
则.
故本题选:.
2.
【详解】解:,,,
,
,
又一个锐角的正切值随锐角度数的增大而增大,
.
故本题选:.
3.
【详解】解:如图,延长交网格于点,连接,由网格以及正方形的性质可得,
由网格构造直角三角形可得,,,
在中,.
故本题选:.
4.
【详解】解:如图,连接,交于点,
由题意可得:,,
设,则,
故,
则.
故本题选:.
5.
【详解】解:四边形为矩形,
,,
矩形沿直线折叠,顶点恰好落在边上的处,
,,
在中,,
,
设,则,
在中,,
,解得,
.
故本题选:.
二.填空题
6.
【详解】解:如图,作于点,
则.
,
.
故本题答案为:.
7.
【详解】解:如图,连接,
由网格可得:,,
,
为等腰直角三角形,
,
则.
故本题答案为:1.
8.
【详解】解:如图,连接,
在正方形、中,
,
,
,
设,,
,,
.
故本题答案为:.
9.
【详解】解:如图,记垂足为D,
由格点知:,
.
,
,
,
.
.
.
10.
【详解】解:由旋转的性质可知,,
,
,,
,
,
,
,
,
.
面积为,
.
故本题答案为:8.
11.
【详解】解:如图,设交轴于,连接,则是直径,
在中,,,
则,
,
由圆周角定理得:,
则.
故本题答案为:.
12.
【详解】解:分两种情况:
①如图1,是边上的中线,,
设,则,
在中,,
,
;
②如图2,是边上的中线,,
设,则,
在中,,
,
,
,
,
综上,所求值为或.
故本题答案为或.
13.
【详解】解:如图,过作轴于点,过作轴于,
则,
顶点,分别在反比例函数与的图象上,
,,
,
,
,
,
,
,
,
,
故本题答案为:.
三.解答题
14.解:如图,过点作于,
,
,
,
,
,
.
15.解: (1),,
,,
在中,,
,又,
则;
(2) 在中,,
设,则,又,
利用勾股定理得:,
解得:或(舍 去) ,
则.
16.解:如图,作直径,连接,
和都对弧,
,
圆的半径是,
,
为直径,
,
,
.
17.解:(1)如图1所示:
(2)如图2所示.
18.(1)证明:四边形内接于,
.
,
,
;
(2)证明:如图,过作于,
是的中点,
,
又于,
,
,
,
,
,
,即,
又,
;
(3)解:是中点,,
,
①,
,
②,
联立①②得:,
,
,
,
,
,
.
19.解法一:如图,设与交于点,
,,
是的中位线,
,,
,
.
,
设,则,
,解得:,
,
,
,
在中,,
.
解法二:如图,
取格点,连接,,
,,
四边形为平行四边形,
,
,
,
,
,
,
为直角三角形,
.
20.解:(1),,
发现结论:,
故本题答案为:,,;
(2)在中,,,,
,
如图,延长至,使得,
,
,
,,
;
(3)①如图,作的垂直平分线交于,连接,
则,,,
中,,,,
,,
设,则,
在中,,
解得:,即,,
;
②如图,作交于点,使,
则.
设,则,
,
,即,
,
在中,,
即,
整理得:,
解得:,(不合题意,舍去),
即,,
.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
