期末真题重组卷(含解析)-2023-2024学年高一数学下学期苏教版2019必修第二册
文档属性
| 名称 | 期末真题重组卷(含解析)-2023-2024学年高一数学下学期苏教版2019必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-05 13:56:34 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末真题重组卷-2023-2024学年高一数学下学期苏教版2019必修第二册
一、单选题
1.(23-24高一下·浙江绍兴·期末)复数的共轭复数是( )
A. B. C. D.
2.(23-24高一下·青海海南·期末)某超市举行购物抽奖活动,规定购物消费每满188元就送一次抽奖机会,中奖的概率为,则下列说法正确的是( )
A.某人抽奖100次,一定能中奖15次 B.某人抽奖200次,至少能中奖3次
C.某人抽奖1次,一定不能中奖 D.某人抽奖20次,可能1次也没中奖
3.(23-24高一下·广东广州·期末)已知一个矩形较长边长为2用斜二测画法画出矩形的直观图是菱形,则直观图的面积为( )
A. B. C. D.
4.(23-24高一上·新疆昌吉·期末)已知.则下列结论错误的是( )
A. B.
C. D.
5.(23-24高一下·辽宁锦州·期末)已知l,m为两条不同的直线,,为两个不同的平面,则下列命题正确的是( )
A.若,,,则
B.若,,则
C.若,,,,则
D.若,,则
6.(23-24高一下·吉林通化·期末)在正四棱锥中,是棱的中点,则点到直线的距离是( )
A. B. C. D.
7.(23-24高一下·陕西宝鸡·期末)已知满足,,,则点依次是的( )
A.重心,外心,垂心 B.重心,外心,内心
C.外心,重心,垂心 D.外心,重心,内心
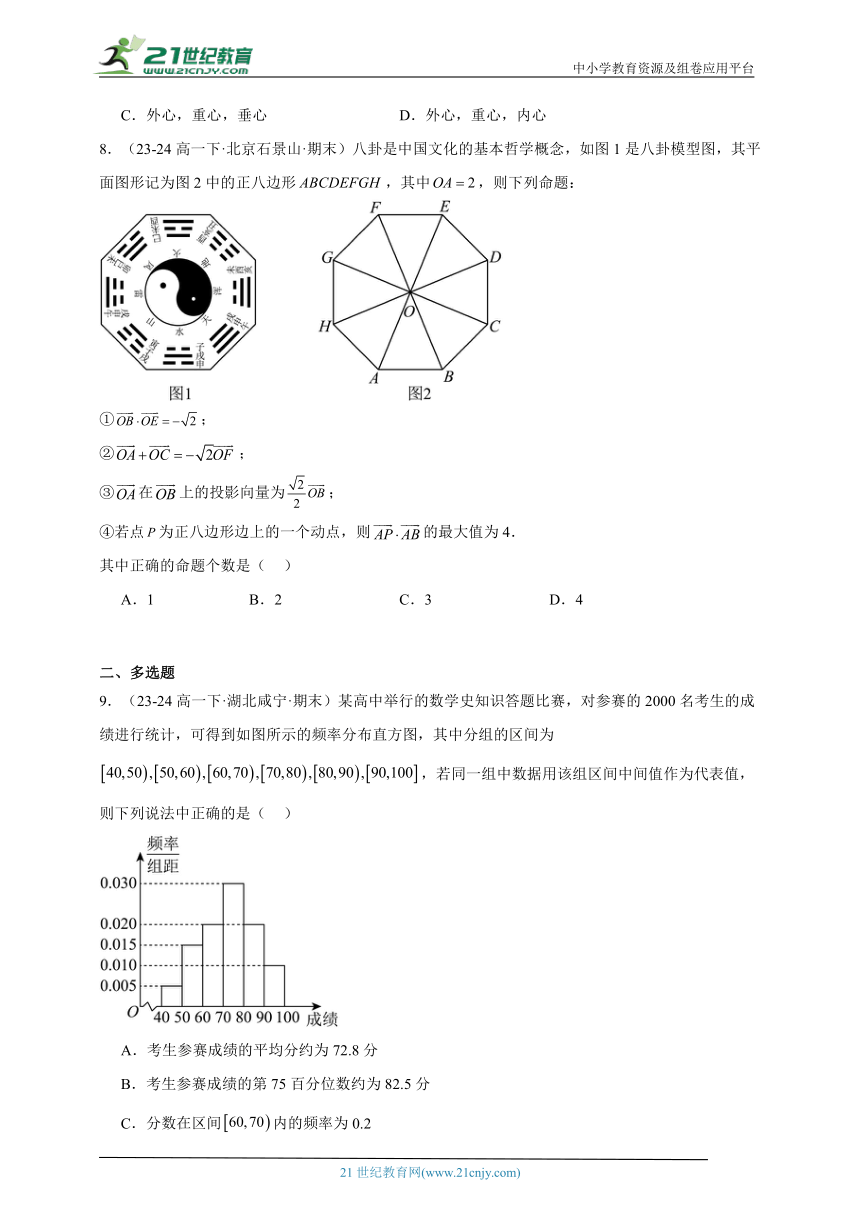
8.(23-24高一下·北京石景山·期末)八卦是中国文化的基本哲学概念,如图1是八卦模型图,其平面图形记为图2中的正八边形,其中,则下列命题:
①;
②;
③在上的投影向量为;
④若点为正八边形边上的一个动点,则的最大值为4.
其中正确的命题个数是( )
A.1 B.2 C.3 D.4
二、多选题
9.(23-24高一下·湖北咸宁·期末)某高中举行的数学史知识答题比赛,对参赛的2000名考生的成绩进行统计,可得到如图所示的频率分布直方图,其中分组的区间为,若同一组中数据用该组区间中间值作为代表值,则下列说法中正确的是( )
A.考生参赛成绩的平均分约为72.8分
B.考生参赛成绩的第75百分位数约为82.5分
C.分数在区间内的频率为0.2
D.用分层抽样的方法从该校学生中抽取一个容量为200的样本,则成绩在区间应抽取30人
10.(23-24高一下·湖北咸宁·期末)已知向量,则下列说法正确的是( )
A.若,则
B.在上的投影向量为
C.若与的夹角为锐角,则
D.若要使最小,则
11.(23-24高一下·辽宁葫芦岛·期末)在中,为边上一动点,则( )
A.
B.的外接圆半径为
C.当为角的角平分线时,
D.当为中点时,
三、填空题
12.(23-24高一下·辽宁锦州·期末)已知,,则的值为 .
13.(23-24高一下·吉林长春·期末)冰雹猜想又称考拉兹猜想、角谷猜想、猜想等,其描述为:任一正整数,如果是奇数就乘以3再加1,如果是偶数就除以2,反复计算,最终都将会得到数字1.例如:给出正整数5,则进行这种反复运算的过程为,即按照这种运算规律进行5次运算后得到1.若从正整数6,7,8,9,10中任取2个数按照上述运算规律进行运算,则运算次数均为奇数的概率为 .
14.(23-24高一下·辽宁葫芦岛·期末)足球起源于中国古代的蹴鞠游戏,“蹴”有用脚蹴 踢的含义,“鞠”最早系外包皮革内饰米糠的球,因而“蹴鞠”就是指古人以脚蹴 踢皮球的活动.已知某鞠(球)的表面上有四个点,满足平面,若三棱锥体积为,则该“鞠”的体积最小值为 .
四、解答题
15.(23-24高一下·吉林·期末)已知复数是一元二次方程()的根.
(1)求的值;
(2)若复数(其中)为纯虚数,求复数的模.
16.(23-24高一下·湖北武汉·期末)在中,角A,B,C所对的边分别为a,b,c,,其中S为的面积.
(1)求角A;
(2)若,求周长的取值范围.
17.(23-24高一下·黑龙江佳木斯·期末)已知向量,.
(1)若,求实数的值;
(2)若,求实数的值.
(3)求向量与向量的夹角余弦值.
18.(23-24高一下·贵州安顺·期末)树人中学为了学生的身心健康,加强食堂用餐质量(简称“美食”)的过程中,后勤部门需了解学生对“美食”工作的认可程度,若学生认可系数不低于0.85、“美食”工作按原方案继续实施,否则需进一步整改.为此后勤部门随机调查了该校600名学生,根据这600名学生对“美食”工作认可程度给出的评分,分成五组,得到如图所示的频率分布直方图.
(1)求频率分布直方图中的值和第70百分位数(结果保留两位小数);
(2)为了解部分学生给“美食”工作评分较低的原因,后勤部门从评分低于80分的学生中,按照调查评分的分组,分为3层,通过分层随机抽样抽取30人进行座谈,求应选取评分在的学生人数;
(3)根据你所学的统计知识,结合认可系数,判断“美食”工作是否需要进一步整改,并说明理由.
19.(23-24高一下·河北唐山·期末)如图,在三棱柱中,,侧面为矩形.
(1)记平面与平面交线为,证明:;
(2)证明:为等边三角形;
(3)若,且为棱的中点,求平面与平面所成二面角的正弦值.
参考答案:
1.B
【分析】根据共轭复数的定义可以求得.
【详解】由共轭复数的定义可得,复数的共轭复数为,
故选:B.
2.D
【分析】中奖的概率为,只能说有中奖的可能性,但不能确定一定中奖还是不中奖,分析判断即可.
【详解】中奖的概率为,与抽的次数无关,只是有中奖的可能性,
故选:D.
3.A
【分析】根据直观图是菱形可得答案.
【详解】如图,是矩形的直观图,则,,,
所以的高为,
则直观图的面积为.
故选:A.
4.C
【分析】根据同角三角形函数的平方关系、商数关系,结合二倍角公式,转化求值即可.
【详解】A.,故选项正确,不符合题意;
B.,故选项正确,不符合题意;
C.,故选项不正确,符合题意;
D.,故选项正确,不符合题意.
故选:C.
5.D
【分析】由线面平行、垂直的判定、性质定理与面面平行的关系依次判断各选项即可得出结果.
【详解】对A:若,,,则,,或,则A错误;
对B:若,,则或,则B错误;
对C:若,,,,若相交时,则;
若时,不一定成立,故C错误;
对D:若,,则,故D正确.
故选:D
6.D
【分析】先根据几何图形特征求出,再应用余弦定理求解即可.
【详解】
在中,
在中,因为
由余弦定理得.
在中,因为,
由余弦定理得.
过B作
在中,由余弦定理得
因为所以.
故选:D.
7.C
【分析】根据到三角形三个顶点的距离相等,得到为外心;根据中线的性质,可得为重心;根据向量垂直,即得到是垂心.
【详解】因为,即到的三个顶点的距离相等,所以为的外心;
设中点为,,,
所在直线经过中点,与边的中线共线,
同理可得,分别与,边的中线共线,是三角形中三条中线的交点,为的重心;
,,,,
同理可得,,所以为的垂心.
故选:C
8.C
【分析】正八边形中,每个边所对的角都是,中心到各顶点的距离为2,然后再由数量积的运算判断①②,由投影向量和投影数量判断③④得答案.
【详解】由题意可知,正八边形每个边所对的角都是,中心到各顶点的距离为2,
对于①,,故①错误;
对于②,,则以,为邻边的对角线长是的倍,
可得,故②正确;
对于③,在上的投影向量为,故③正确;
对于④,设的夹角为,则,其中表示在上的投影数量,
易知,延长DC交AB延长线于Q,当P在线段DC上运动,投影数量最大,
易知为等腰直角三角形,且,
则在中,,
在等腰三角形中,
则
.故④正确.
则正确的个数共有3个.
故选:C.
【点睛】关键点点睛:本题问题④的关键是利用数量积的几何意义确定在上的投影的最大值.
9.BC
【分析】对A,确定每组数据中间值,以及每组数据的频率代入到求平均数的公式即可求得;对B,第75百分位数得到位于内,代入公式可计算第75百分位数值;对C,分数在区间内的频率为0.2可判断;对D,用分层随机抽样可得区间应抽取60人,即得到答案.
【详解】对A,平均成绩
为,故A错误;
对B,由频率分布直方图知第75百分位数位于内,
则第75百分位数为,故B正确;
对C,分数在区间内的频率为,故C正确;
对D,区间应抽取人,故D错误.
故选:BC
10.ABD
【分析】A选项,由向量加法和向量平行的坐标运算求解;B选项,由投影向量的公式计算;C选项,由向量夹角的范围,利用向量共线和向量数量积求参数取值范围;D选项,由向量线性运算的坐标表示和模长公式,结合二次函数的性质求满足条件的t的值.
【详解】对于A:因为,所以.
又,且,所以,解得:,故A正确;
对于B:由,则,
所以在上的投影向量为,故B正确;
对于C:当与共线时,有,此时与方向相同,
当与的夹角为锐角,有,解得,
所以且时,与的夹角为锐角,故C错误;
对于D:由,,
结合二次函数的性质可知,时取最小值,故D正确.
故选:ABD.
11.ABC
【分析】对于A,由余弦定理即可得解;对于B,由A结合正弦定理即可得解;对于C,由计算即可得解;对于D,由两边平方计算即可得解.
【详解】对于A,由题意及余弦定理得,
,故A正确;
对于B,由A结合正弦定理可知的外接圆半径为,故B正确;
对于C,当为角的角平分线时,则由,
得,
所以,
即,故C正确;
对于D,当为中点时,有,
所以
,
所以,故D错误.
故选:ABC.
12./0.5
【分析】由两角和的三角函数公式化简即可求得结果.
【详解】,,则,
所以,.
故答案为:
13./0.1
【分析】根据题中定义,分别求出正整数6,7,8,9,10按照题中所给运算规律进行运算的次数,最后根据古典概型的概率计算公式进行求解即可.
【详解】按照题中运算规律,正整数6的运算过程为,运算次数为;
正整数7的部分运算过程为,
当运算到10时,运算次数为10,由正整数的运算过程可知,正整数7总的运算次数为;
正整数8的运算次数为;
正整数9的部分运算过程为,当运算到7时,运算次数为3,
由正整数7的运算过程可知,正整数9总的运算次数为;
正整数10的运算次数为6;
故正整数6,7,8,9,10的运算次数分别为偶数、偶数、奇数、奇数、偶数,
从正整数6,7,8,9,10中任取2个数的方法总数为:
,共种,
其中的运算次数均为奇数的方法总数为:,共种,
故运算次数均为奇数的概率为.
故答案为:
14.
【分析】根据三棱锥的外接球的球心到所有顶点距离相等,且都为球半径,即可找到球心的位置,然后在直角三角形中,根据基本不等式即可求解最小值,进而可得球半径的最小值.
【详解】
取中点为,过作交于,则,即为中点.
因为平面,所以平面.
因为,所以,
所以,,
所以,是三棱锥外接球球心,为球的半径.
由,
又,当且仅当,等号成立,此时,
所以球半径,故,
该“鞠”的体积最小值为
故答案为:.
15.(1)
(2)
【分析】根据是一元二次方程的根得到也是一元二次方程的根,代入列方程组求解即可;
(2)求出,根据复数为纯虚数求出即可求出.
【详解】(1)因为是一元二次方程的根,
所以也是一元二次方程的根,
故,解得;
(2)因为复数为纯虚数,
所以,且,
即,所以复数,
故.
16.(1)
(2)
【分析】(1)利用三角形面积公式与余弦定理代入已知条件,整理得,从而得解;
(2)利用基本不等式与两边之和大于第三边求得,进而得解.
【详解】(1)因为,,,
所以,则,即,
又,所以.
(2)的周长为,
因为,即,
因为,所以,
所以,则,即,
又,所以,即,
所以的周长的取值范围为.
17.(1)
(2)
(3).
【分析】(1)首先求出,的坐标,再根据平面向量共线的坐标表示得到方程,解得即可;
(2)首先求出的坐标,依题意可得,根据数量积的坐标表示得到方程,解得即可;
(3)首先求出的坐标,再根据夹角公式计算可得.
【详解】(1)因为,,
所以,
,
∵,∴,
解得.
(2)由题意得,,
∵,∴,
解得.
(3)因为,
所以,,
又,
设向量与向量的夹角为,
所以.
18.(1)0.01,88.33;
(2)10人;
(3)“美食”工作需要进一步整改,理由见解析.
【分析】(1)根据频率分布图,求得,然后推得第70百分位数位于区间内,即可根据第百分位数的求法,得出答案.
(2)根据分层抽样,即可求得评分在的学生人数.
(3)根据频率分布直方图,即可求得平均数,进而得出答案.
【详解】(1)由图可知:,所以;
评分在内的频率为,内的频率为,
则第70百分位数位,,
所以第70百分位数为88.33.
(2)低于80分的学生中三组学生的人数比例为,
则应选取评分在的学生人数为:(人).
(3)由图可知,认可程度平均分为:
,
显然认可系数低于,所以 “美食”工作需要进一步整改.
19.(1)证明见解析
(2)证明见解析
(3)
【分析】(1)首先证明平面,由线面平行的性质即可证明;
(2)取的中点,棱的中点,证明平面,
得到,从而证明为等边三角形;
(3)连接,交于,可得平面与平面
所成二面角为或的补角,利用余弦定理即可求解.
【详解】(1)因为在三棱柱中,,
由于平面,平面,
所以平面,
又因为平面,平面平面,
所以
(2)取的中点,棱的中点,连接,
因为,为的中点,
所以,
又因为侧面为矩形.,为的中点,为棱的中点,
所以
因为,平面,平面,
所以平面,
因为平面,
所以,
因为在三棱柱中,,
所以,
又因为为棱的中点,
所以
又因为在三棱柱中,,,
所以,
又因为,
则,所以为等边三角形
(3)连接,交于,则为的中点,
因为为的中点,为棱的中点,
所以,
又因为在三棱柱中,,
所以,,
所以四边形为平行四边形,
则平面即平面,
则平面平面
所以平面与平面所成二面角,即为平面与平面所成二面角,
因为,
所以,,,
则,所以,
因为为的中点,所以,
所以,,
取的中点,连接,,
所以,,且,,
所以平面与平面所成二面角为或的补角,
因为在中,,,,
所以,
所以平面与平面所成二面角的正弦值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题重组卷-2023-2024学年高一数学下学期苏教版2019必修第二册
一、单选题
1.(23-24高一下·浙江绍兴·期末)复数的共轭复数是( )
A. B. C. D.
2.(23-24高一下·青海海南·期末)某超市举行购物抽奖活动,规定购物消费每满188元就送一次抽奖机会,中奖的概率为,则下列说法正确的是( )
A.某人抽奖100次,一定能中奖15次 B.某人抽奖200次,至少能中奖3次
C.某人抽奖1次,一定不能中奖 D.某人抽奖20次,可能1次也没中奖
3.(23-24高一下·广东广州·期末)已知一个矩形较长边长为2用斜二测画法画出矩形的直观图是菱形,则直观图的面积为( )
A. B. C. D.
4.(23-24高一上·新疆昌吉·期末)已知.则下列结论错误的是( )
A. B.
C. D.
5.(23-24高一下·辽宁锦州·期末)已知l,m为两条不同的直线,,为两个不同的平面,则下列命题正确的是( )
A.若,,,则
B.若,,则
C.若,,,,则
D.若,,则
6.(23-24高一下·吉林通化·期末)在正四棱锥中,是棱的中点,则点到直线的距离是( )
A. B. C. D.
7.(23-24高一下·陕西宝鸡·期末)已知满足,,,则点依次是的( )
A.重心,外心,垂心 B.重心,外心,内心
C.外心,重心,垂心 D.外心,重心,内心
8.(23-24高一下·北京石景山·期末)八卦是中国文化的基本哲学概念,如图1是八卦模型图,其平面图形记为图2中的正八边形,其中,则下列命题:
①;
②;
③在上的投影向量为;
④若点为正八边形边上的一个动点,则的最大值为4.
其中正确的命题个数是( )
A.1 B.2 C.3 D.4
二、多选题
9.(23-24高一下·湖北咸宁·期末)某高中举行的数学史知识答题比赛,对参赛的2000名考生的成绩进行统计,可得到如图所示的频率分布直方图,其中分组的区间为,若同一组中数据用该组区间中间值作为代表值,则下列说法中正确的是( )
A.考生参赛成绩的平均分约为72.8分
B.考生参赛成绩的第75百分位数约为82.5分
C.分数在区间内的频率为0.2
D.用分层抽样的方法从该校学生中抽取一个容量为200的样本,则成绩在区间应抽取30人
10.(23-24高一下·湖北咸宁·期末)已知向量,则下列说法正确的是( )
A.若,则
B.在上的投影向量为
C.若与的夹角为锐角,则
D.若要使最小,则
11.(23-24高一下·辽宁葫芦岛·期末)在中,为边上一动点,则( )
A.
B.的外接圆半径为
C.当为角的角平分线时,
D.当为中点时,
三、填空题
12.(23-24高一下·辽宁锦州·期末)已知,,则的值为 .
13.(23-24高一下·吉林长春·期末)冰雹猜想又称考拉兹猜想、角谷猜想、猜想等,其描述为:任一正整数,如果是奇数就乘以3再加1,如果是偶数就除以2,反复计算,最终都将会得到数字1.例如:给出正整数5,则进行这种反复运算的过程为,即按照这种运算规律进行5次运算后得到1.若从正整数6,7,8,9,10中任取2个数按照上述运算规律进行运算,则运算次数均为奇数的概率为 .
14.(23-24高一下·辽宁葫芦岛·期末)足球起源于中国古代的蹴鞠游戏,“蹴”有用脚蹴 踢的含义,“鞠”最早系外包皮革内饰米糠的球,因而“蹴鞠”就是指古人以脚蹴 踢皮球的活动.已知某鞠(球)的表面上有四个点,满足平面,若三棱锥体积为,则该“鞠”的体积最小值为 .
四、解答题
15.(23-24高一下·吉林·期末)已知复数是一元二次方程()的根.
(1)求的值;
(2)若复数(其中)为纯虚数,求复数的模.
16.(23-24高一下·湖北武汉·期末)在中,角A,B,C所对的边分别为a,b,c,,其中S为的面积.
(1)求角A;
(2)若,求周长的取值范围.
17.(23-24高一下·黑龙江佳木斯·期末)已知向量,.
(1)若,求实数的值;
(2)若,求实数的值.
(3)求向量与向量的夹角余弦值.
18.(23-24高一下·贵州安顺·期末)树人中学为了学生的身心健康,加强食堂用餐质量(简称“美食”)的过程中,后勤部门需了解学生对“美食”工作的认可程度,若学生认可系数不低于0.85、“美食”工作按原方案继续实施,否则需进一步整改.为此后勤部门随机调查了该校600名学生,根据这600名学生对“美食”工作认可程度给出的评分,分成五组,得到如图所示的频率分布直方图.
(1)求频率分布直方图中的值和第70百分位数(结果保留两位小数);
(2)为了解部分学生给“美食”工作评分较低的原因,后勤部门从评分低于80分的学生中,按照调查评分的分组,分为3层,通过分层随机抽样抽取30人进行座谈,求应选取评分在的学生人数;
(3)根据你所学的统计知识,结合认可系数,判断“美食”工作是否需要进一步整改,并说明理由.
19.(23-24高一下·河北唐山·期末)如图,在三棱柱中,,侧面为矩形.
(1)记平面与平面交线为,证明:;
(2)证明:为等边三角形;
(3)若,且为棱的中点,求平面与平面所成二面角的正弦值.
参考答案:
1.B
【分析】根据共轭复数的定义可以求得.
【详解】由共轭复数的定义可得,复数的共轭复数为,
故选:B.
2.D
【分析】中奖的概率为,只能说有中奖的可能性,但不能确定一定中奖还是不中奖,分析判断即可.
【详解】中奖的概率为,与抽的次数无关,只是有中奖的可能性,
故选:D.
3.A
【分析】根据直观图是菱形可得答案.
【详解】如图,是矩形的直观图,则,,,
所以的高为,
则直观图的面积为.
故选:A.
4.C
【分析】根据同角三角形函数的平方关系、商数关系,结合二倍角公式,转化求值即可.
【详解】A.,故选项正确,不符合题意;
B.,故选项正确,不符合题意;
C.,故选项不正确,符合题意;
D.,故选项正确,不符合题意.
故选:C.
5.D
【分析】由线面平行、垂直的判定、性质定理与面面平行的关系依次判断各选项即可得出结果.
【详解】对A:若,,,则,,或,则A错误;
对B:若,,则或,则B错误;
对C:若,,,,若相交时,则;
若时,不一定成立,故C错误;
对D:若,,则,故D正确.
故选:D
6.D
【分析】先根据几何图形特征求出,再应用余弦定理求解即可.
【详解】
在中,
在中,因为
由余弦定理得.
在中,因为,
由余弦定理得.
过B作
在中,由余弦定理得
因为所以.
故选:D.
7.C
【分析】根据到三角形三个顶点的距离相等,得到为外心;根据中线的性质,可得为重心;根据向量垂直,即得到是垂心.
【详解】因为,即到的三个顶点的距离相等,所以为的外心;
设中点为,,,
所在直线经过中点,与边的中线共线,
同理可得,分别与,边的中线共线,是三角形中三条中线的交点,为的重心;
,,,,
同理可得,,所以为的垂心.
故选:C
8.C
【分析】正八边形中,每个边所对的角都是,中心到各顶点的距离为2,然后再由数量积的运算判断①②,由投影向量和投影数量判断③④得答案.
【详解】由题意可知,正八边形每个边所对的角都是,中心到各顶点的距离为2,
对于①,,故①错误;
对于②,,则以,为邻边的对角线长是的倍,
可得,故②正确;
对于③,在上的投影向量为,故③正确;
对于④,设的夹角为,则,其中表示在上的投影数量,
易知,延长DC交AB延长线于Q,当P在线段DC上运动,投影数量最大,
易知为等腰直角三角形,且,
则在中,,
在等腰三角形中,
则
.故④正确.
则正确的个数共有3个.
故选:C.
【点睛】关键点点睛:本题问题④的关键是利用数量积的几何意义确定在上的投影的最大值.
9.BC
【分析】对A,确定每组数据中间值,以及每组数据的频率代入到求平均数的公式即可求得;对B,第75百分位数得到位于内,代入公式可计算第75百分位数值;对C,分数在区间内的频率为0.2可判断;对D,用分层随机抽样可得区间应抽取60人,即得到答案.
【详解】对A,平均成绩
为,故A错误;
对B,由频率分布直方图知第75百分位数位于内,
则第75百分位数为,故B正确;
对C,分数在区间内的频率为,故C正确;
对D,区间应抽取人,故D错误.
故选:BC
10.ABD
【分析】A选项,由向量加法和向量平行的坐标运算求解;B选项,由投影向量的公式计算;C选项,由向量夹角的范围,利用向量共线和向量数量积求参数取值范围;D选项,由向量线性运算的坐标表示和模长公式,结合二次函数的性质求满足条件的t的值.
【详解】对于A:因为,所以.
又,且,所以,解得:,故A正确;
对于B:由,则,
所以在上的投影向量为,故B正确;
对于C:当与共线时,有,此时与方向相同,
当与的夹角为锐角,有,解得,
所以且时,与的夹角为锐角,故C错误;
对于D:由,,
结合二次函数的性质可知,时取最小值,故D正确.
故选:ABD.
11.ABC
【分析】对于A,由余弦定理即可得解;对于B,由A结合正弦定理即可得解;对于C,由计算即可得解;对于D,由两边平方计算即可得解.
【详解】对于A,由题意及余弦定理得,
,故A正确;
对于B,由A结合正弦定理可知的外接圆半径为,故B正确;
对于C,当为角的角平分线时,则由,
得,
所以,
即,故C正确;
对于D,当为中点时,有,
所以
,
所以,故D错误.
故选:ABC.
12./0.5
【分析】由两角和的三角函数公式化简即可求得结果.
【详解】,,则,
所以,.
故答案为:
13./0.1
【分析】根据题中定义,分别求出正整数6,7,8,9,10按照题中所给运算规律进行运算的次数,最后根据古典概型的概率计算公式进行求解即可.
【详解】按照题中运算规律,正整数6的运算过程为,运算次数为;
正整数7的部分运算过程为,
当运算到10时,运算次数为10,由正整数的运算过程可知,正整数7总的运算次数为;
正整数8的运算次数为;
正整数9的部分运算过程为,当运算到7时,运算次数为3,
由正整数7的运算过程可知,正整数9总的运算次数为;
正整数10的运算次数为6;
故正整数6,7,8,9,10的运算次数分别为偶数、偶数、奇数、奇数、偶数,
从正整数6,7,8,9,10中任取2个数的方法总数为:
,共种,
其中的运算次数均为奇数的方法总数为:,共种,
故运算次数均为奇数的概率为.
故答案为:
14.
【分析】根据三棱锥的外接球的球心到所有顶点距离相等,且都为球半径,即可找到球心的位置,然后在直角三角形中,根据基本不等式即可求解最小值,进而可得球半径的最小值.
【详解】
取中点为,过作交于,则,即为中点.
因为平面,所以平面.
因为,所以,
所以,,
所以,是三棱锥外接球球心,为球的半径.
由,
又,当且仅当,等号成立,此时,
所以球半径,故,
该“鞠”的体积最小值为
故答案为:.
15.(1)
(2)
【分析】根据是一元二次方程的根得到也是一元二次方程的根,代入列方程组求解即可;
(2)求出,根据复数为纯虚数求出即可求出.
【详解】(1)因为是一元二次方程的根,
所以也是一元二次方程的根,
故,解得;
(2)因为复数为纯虚数,
所以,且,
即,所以复数,
故.
16.(1)
(2)
【分析】(1)利用三角形面积公式与余弦定理代入已知条件,整理得,从而得解;
(2)利用基本不等式与两边之和大于第三边求得,进而得解.
【详解】(1)因为,,,
所以,则,即,
又,所以.
(2)的周长为,
因为,即,
因为,所以,
所以,则,即,
又,所以,即,
所以的周长的取值范围为.
17.(1)
(2)
(3).
【分析】(1)首先求出,的坐标,再根据平面向量共线的坐标表示得到方程,解得即可;
(2)首先求出的坐标,依题意可得,根据数量积的坐标表示得到方程,解得即可;
(3)首先求出的坐标,再根据夹角公式计算可得.
【详解】(1)因为,,
所以,
,
∵,∴,
解得.
(2)由题意得,,
∵,∴,
解得.
(3)因为,
所以,,
又,
设向量与向量的夹角为,
所以.
18.(1)0.01,88.33;
(2)10人;
(3)“美食”工作需要进一步整改,理由见解析.
【分析】(1)根据频率分布图,求得,然后推得第70百分位数位于区间内,即可根据第百分位数的求法,得出答案.
(2)根据分层抽样,即可求得评分在的学生人数.
(3)根据频率分布直方图,即可求得平均数,进而得出答案.
【详解】(1)由图可知:,所以;
评分在内的频率为,内的频率为,
则第70百分位数位,,
所以第70百分位数为88.33.
(2)低于80分的学生中三组学生的人数比例为,
则应选取评分在的学生人数为:(人).
(3)由图可知,认可程度平均分为:
,
显然认可系数低于,所以 “美食”工作需要进一步整改.
19.(1)证明见解析
(2)证明见解析
(3)
【分析】(1)首先证明平面,由线面平行的性质即可证明;
(2)取的中点,棱的中点,证明平面,
得到,从而证明为等边三角形;
(3)连接,交于,可得平面与平面
所成二面角为或的补角,利用余弦定理即可求解.
【详解】(1)因为在三棱柱中,,
由于平面,平面,
所以平面,
又因为平面,平面平面,
所以
(2)取的中点,棱的中点,连接,
因为,为的中点,
所以,
又因为侧面为矩形.,为的中点,为棱的中点,
所以
因为,平面,平面,
所以平面,
因为平面,
所以,
因为在三棱柱中,,
所以,
又因为为棱的中点,
所以
又因为在三棱柱中,,,
所以,
又因为,
则,所以为等边三角形
(3)连接,交于,则为的中点,
因为为的中点,为棱的中点,
所以,
又因为在三棱柱中,,
所以,,
所以四边形为平行四边形,
则平面即平面,
则平面平面
所以平面与平面所成二面角,即为平面与平面所成二面角,
因为,
所以,,,
则,所以,
因为为的中点,所以,
所以,,
取的中点,连接,,
所以,,且,,
所以平面与平面所成二面角为或的补角,
因为在中,,,,
所以,
所以平面与平面所成二面角的正弦值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
