5.3.1等比数列(二) 课件(共18张PPT) 2023-2024学年高二数学同步讲义(人教B版2019选择性必修第三册)
文档属性
| 名称 | 5.3.1等比数列(二) 课件(共18张PPT) 2023-2024学年高二数学同步讲义(人教B版2019选择性必修第三册) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-05 15:39:03 | ||
图片预览






文档简介
(共18张PPT)
5.3.1等比数列(二)
前面我们一起对等差数列、等比数列的有关知识进行了探索与研究,对比等差数列的有关性质,等比数列是否也具有类似的性质呢?
1. 理解等比中项的概念,能用公式求解;(重点)
2. 掌握判断等比数列的常用方法;(重点)
3. 能通过等比数列的概念、通项公式了解等比数列的性质,并能灵活运用于解决问题.(难点)
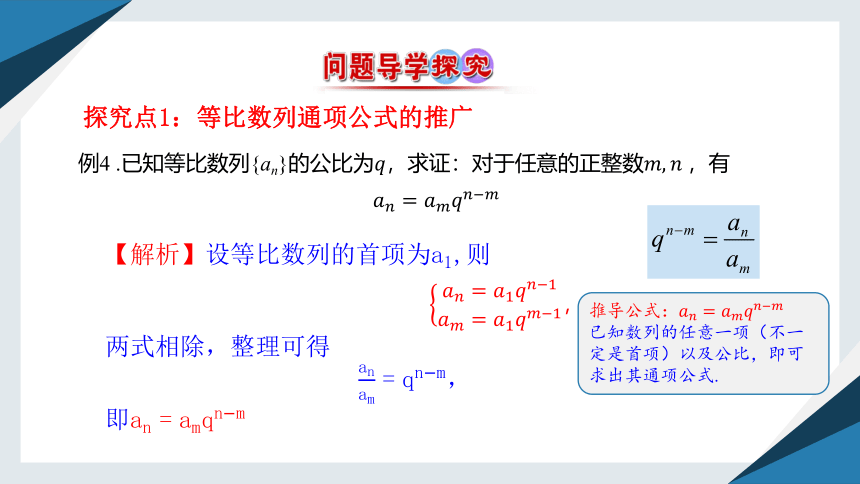
探究点1:等比数列通项公式的推广
例4 .已知等比数列{an}的公比为,求证:对于任意的正整数有
【解析】设等比数列的首项为,则
两式相除,整理可得
,
即
,
推导公式:
已知数列的任意一项(不一定是首项)以及公比,即可求出其通项公式.
例5.已知等比数列{an}中,,,求.
【解析】(方法一)设等比数列的首项为,公比为,则
解得 ,,因此
通性通法
基本量的运算
(方法二)设等比数列的公比为
根据推导公式
所以
将已知条件代入,可得 ,
又,解得.
探究点2:等比中项
思考1:请同学们结合等差中项的定义,考虑一下等比数列是否具有此类性质呢?又是如何描述的?
等比中项的概念
如果是等比数列,那么称为与的等比中项.
= →
例如:2与8的等比中项是
两个正数的等比中项有两个
容易看出,在一个等比数列中,从第2项起,每一项(有穷数列的末项除外)都是它的前一项与后一项的等比中项;反之,如果一个数列从第2项起,每一项(有穷数列的末项除外)都是它的前一项与后一项的等比中项,那么这个数列是等比数列.
追问1:一个等比数列是1,2,4,8,16,32,64.请问8是谁的等比中项呢?
【拓展提升】对等比中项的理解:
1,2,4,8,16,32,64
追问2:对任意两个不为零的数是否一定都有等比中项?若有是否唯一?
提示:不一定,只有当两个数同号,即两个数之积大于零时,此两数才有等比中项且有两个等比中项,它们互为相反数.
追问3:为与的等比中项的充要条件是=吗?
提示:不是,在中,若=0,则,中至少有一个为0,此时三个数不成等比数列;若,,,均为非零常
数,则,,成等比数列.
例6.如果数列{an}中,在时恒成立,
求证: {an}是等比数列.
探究点3:等比数列的判断方法
【解析】
,
因此,从第2项起,每一项与它的前一项的比都相等,所以{}是等比数列.
是与
的等比中项
等比数列的定义是什么?
【总结】
(1)定义法:若(q为常数),则数列为等比数列;
(2)等比中项法:若(),则数列为等比数列;
(3)通项法:若(k,b为非零常数),则数列为等比数列;
判断一个数列是不是等比数列的几种常用方法
判断一个数列是否为等比数列,可以用以上三种方法,但证明一个数列是等比数列,只能用方法1和方法2.
探究点4:等比数列的性质
思考 1:设数列{an}的通项公式为,求出,并比较它们的大小.
【提示】由易知,数列{}是等比数列,
因为
=,
=,
所以.
思考:类比等差数列,从中你发现了怎样的一般规律?
下标和性质
一般地,如果 是等比数列,而且正整数s, t,p,q满足
s + t = p + q,则
.
性质推广:如果 2s = p + q ( s,p,q ∈N +),则 = pq,即 是与 的等比中项.
以上性质可描述为:
等比数列中,下标和相等的任意两项,它们的积也相等.
即时训练:
1.在等比数列{}中, , ,则=__________.
或-30
30
2.等比数列{}的各项均为正数, ,则
=__________.
【解析】由等比数列的下标和性质可知
.
所以
.
5
例7.在4与之间插入3个数,使这5个数成等比数列,求插入的3个数.
【解析】(方法一)依题意,, ,
由等比数列的通项公式,得,解得
当时,插入的3个数分别为
当时,插入的3个数分别为4×()=-2,-2×()=1,1×()=,
因此插入的3个数分别为或.
(方法二)因为等比数列共有5项,即,,,,.
又因为所以
即,又因为要与同号,所以
类似地,有而且与同号,因此
当 时, ;
当 = 2时, = ;
因此插入的3个数分别为或
思考:常见的等比数列的性质还有哪些?
【提示】(1)等比数列中每隔一定项取出一项按原来顺序排列
构成的数列仍为_________.
(2){}(λ≠0),{||}皆为等比数列,公比分别为______;
(3)若{}和{}分别是公比为q和p的等比数列,则
数列{·},{ }仍是等比数列,它们的公比分别________.
等比数列
5.3.1等比数列(二)
前面我们一起对等差数列、等比数列的有关知识进行了探索与研究,对比等差数列的有关性质,等比数列是否也具有类似的性质呢?
1. 理解等比中项的概念,能用公式求解;(重点)
2. 掌握判断等比数列的常用方法;(重点)
3. 能通过等比数列的概念、通项公式了解等比数列的性质,并能灵活运用于解决问题.(难点)
探究点1:等比数列通项公式的推广
例4 .已知等比数列{an}的公比为,求证:对于任意的正整数有
【解析】设等比数列的首项为,则
两式相除,整理可得
,
即
,
推导公式:
已知数列的任意一项(不一定是首项)以及公比,即可求出其通项公式.
例5.已知等比数列{an}中,,,求.
【解析】(方法一)设等比数列的首项为,公比为,则
解得 ,,因此
通性通法
基本量的运算
(方法二)设等比数列的公比为
根据推导公式
所以
将已知条件代入,可得 ,
又,解得.
探究点2:等比中项
思考1:请同学们结合等差中项的定义,考虑一下等比数列是否具有此类性质呢?又是如何描述的?
等比中项的概念
如果是等比数列,那么称为与的等比中项.
= →
例如:2与8的等比中项是
两个正数的等比中项有两个
容易看出,在一个等比数列中,从第2项起,每一项(有穷数列的末项除外)都是它的前一项与后一项的等比中项;反之,如果一个数列从第2项起,每一项(有穷数列的末项除外)都是它的前一项与后一项的等比中项,那么这个数列是等比数列.
追问1:一个等比数列是1,2,4,8,16,32,64.请问8是谁的等比中项呢?
【拓展提升】对等比中项的理解:
1,2,4,8,16,32,64
追问2:对任意两个不为零的数是否一定都有等比中项?若有是否唯一?
提示:不一定,只有当两个数同号,即两个数之积大于零时,此两数才有等比中项且有两个等比中项,它们互为相反数.
追问3:为与的等比中项的充要条件是=吗?
提示:不是,在中,若=0,则,中至少有一个为0,此时三个数不成等比数列;若,,,均为非零常
数,则,,成等比数列.
例6.如果数列{an}中,在时恒成立,
求证: {an}是等比数列.
探究点3:等比数列的判断方法
【解析】
,
因此,从第2项起,每一项与它的前一项的比都相等,所以{}是等比数列.
是与
的等比中项
等比数列的定义是什么?
【总结】
(1)定义法:若(q为常数),则数列为等比数列;
(2)等比中项法:若(),则数列为等比数列;
(3)通项法:若(k,b为非零常数),则数列为等比数列;
判断一个数列是不是等比数列的几种常用方法
判断一个数列是否为等比数列,可以用以上三种方法,但证明一个数列是等比数列,只能用方法1和方法2.
探究点4:等比数列的性质
思考 1:设数列{an}的通项公式为,求出,并比较它们的大小.
【提示】由易知,数列{}是等比数列,
因为
=,
=,
所以.
思考:类比等差数列,从中你发现了怎样的一般规律?
下标和性质
一般地,如果 是等比数列,而且正整数s, t,p,q满足
s + t = p + q,则
.
性质推广:如果 2s = p + q ( s,p,q ∈N +),则 = pq,即 是与 的等比中项.
以上性质可描述为:
等比数列中,下标和相等的任意两项,它们的积也相等.
即时训练:
1.在等比数列{}中, , ,则=__________.
或-30
30
2.等比数列{}的各项均为正数, ,则
=__________.
【解析】由等比数列的下标和性质可知
.
所以
.
5
例7.在4与之间插入3个数,使这5个数成等比数列,求插入的3个数.
【解析】(方法一)依题意,, ,
由等比数列的通项公式,得,解得
当时,插入的3个数分别为
当时,插入的3个数分别为4×()=-2,-2×()=1,1×()=,
因此插入的3个数分别为或.
(方法二)因为等比数列共有5项,即,,,,.
又因为所以
即,又因为要与同号,所以
类似地,有而且与同号,因此
当 时, ;
当 = 2时, = ;
因此插入的3个数分别为或
思考:常见的等比数列的性质还有哪些?
【提示】(1)等比数列中每隔一定项取出一项按原来顺序排列
构成的数列仍为_________.
(2){}(λ≠0),{||}皆为等比数列,公比分别为______;
(3)若{}和{}分别是公比为q和p的等比数列,则
数列{·},{ }仍是等比数列,它们的公比分别________.
等比数列
