6.1.2导数及其几何意义(二) 课件(共13张PPT) 2023-2024学年高二数学同步讲义(人教B版2019选择性必修第三册)
文档属性
| 名称 | 6.1.2导数及其几何意义(二) 课件(共13张PPT) 2023-2024学年高二数学同步讲义(人教B版2019选择性必修第三册) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-05 15:50:11 | ||
图片预览




文档简介
(共13张PPT)
6.1.2 导数及其几何意义(2)
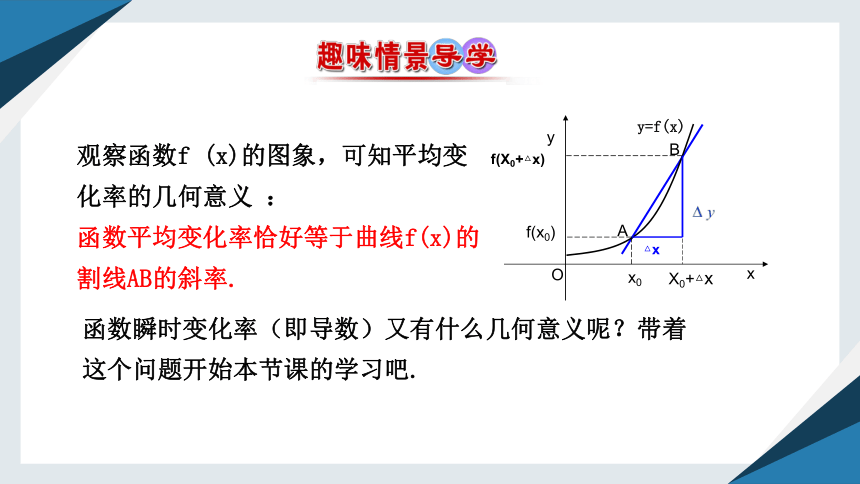
观察函数f (x)的图象,可知平均变
化率的几何意义 :
函数平均变化率恰好等于曲线f(x)的
割线AB的斜率.
O
A
B
x
y
y=f(x)
x0
X0+△x
f(x0)
f(X0+△x)
△x
函数瞬时变化率(即导数)又有什么几何意义呢?带着
这个问题开始本节课的学习吧.
1.理解导数的几何意义.(重点)
2.会求曲线的切线方程. (难点)
探究点1: 曲线的切线
如图,观察当点沿着曲线逐渐向点接近时,割线绕着点逐渐转动的情况.
我们发现,当点沿着曲线无限接近点,即Δx →0时,割线有一个极限位置.则我们把直线称为曲线在点处的 .
A
B
o
x
y
割线
切线
D
S
切线
探究点2:导数的几何意义
如图,继续观察当点沿着曲线逐渐向点接近时,割线绕着点逐渐转动的情况.
这表明,函数在某点处的导数
等于曲线在该点处的 .
A
B
o
x
y
割线
切线
D
斜率为
切线的斜率
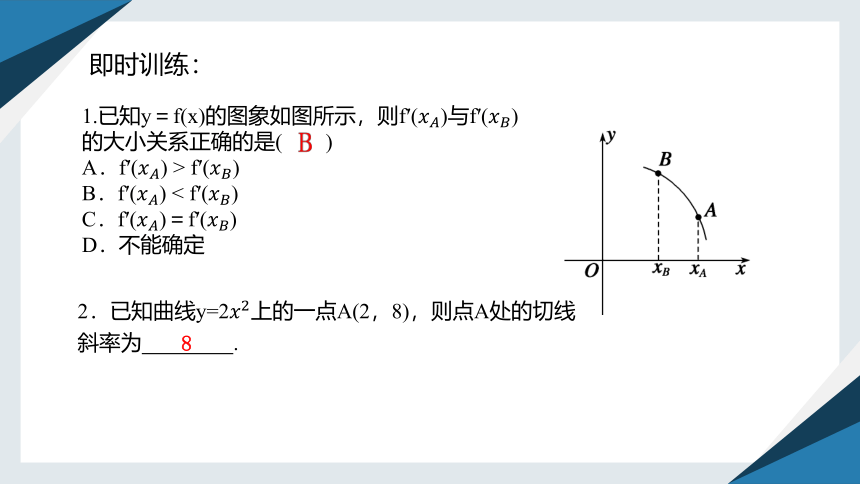
1.已知y=f(x)的图象如图所示,则f′()与f′()
的大小关系正确的是( )
A.f′() > f′()
B.f′() < f′()
C.f′()=f′()
D.不能确定
即时训练:
2.已知曲线y=2上的一点A(2,8),则点A处的切线
斜率为 .
8
例 4.已知函数,求曲线在处切线的斜率与方程.
解:因为
,
因此所求切线的斜率为2.
又因为=1,
所以切线的方程为 ,
即.
切点坐标(1,1)
直线的点斜式方程
求曲线上点)处的切线方程:
(1)根据曲线的函数关系式求出切线斜率;
(2)将代入,求得曲线上点;
(3)根据直线的点斜式方程,得切线方程
【总结】
例 5.已知函数,求曲线在处的切线方程.
解:因为
,
又因为,
所以切线的方程为 ,
即.
求曲线在点(1,3)处的切线方程.
跟踪训练:
解:因为
,
又因为切点坐标为,
所以切线的方程为 ,
即.
探究点3:求函数近似值
f (x0) = .
当很小时,f (x0)
所以,当很小时,
.
以直代曲
例6 .已知函数,计算的近似值.
解:由题意可得,,,
因此
.
导数的几何意义
切线
导数的
几何意义
导数的
应用
切线斜率
求切线方程
6.1.2 导数及其几何意义(2)
观察函数f (x)的图象,可知平均变
化率的几何意义 :
函数平均变化率恰好等于曲线f(x)的
割线AB的斜率.
O
A
B
x
y
y=f(x)
x0
X0+△x
f(x0)
f(X0+△x)
△x
函数瞬时变化率(即导数)又有什么几何意义呢?带着
这个问题开始本节课的学习吧.
1.理解导数的几何意义.(重点)
2.会求曲线的切线方程. (难点)
探究点1: 曲线的切线
如图,观察当点沿着曲线逐渐向点接近时,割线绕着点逐渐转动的情况.
我们发现,当点沿着曲线无限接近点,即Δx →0时,割线有一个极限位置.则我们把直线称为曲线在点处的 .
A
B
o
x
y
割线
切线
D
S
切线
探究点2:导数的几何意义
如图,继续观察当点沿着曲线逐渐向点接近时,割线绕着点逐渐转动的情况.
这表明,函数在某点处的导数
等于曲线在该点处的 .
A
B
o
x
y
割线
切线
D
斜率为
切线的斜率
1.已知y=f(x)的图象如图所示,则f′()与f′()
的大小关系正确的是( )
A.f′() > f′()
B.f′() < f′()
C.f′()=f′()
D.不能确定
即时训练:
2.已知曲线y=2上的一点A(2,8),则点A处的切线
斜率为 .
8
例 4.已知函数,求曲线在处切线的斜率与方程.
解:因为
,
因此所求切线的斜率为2.
又因为=1,
所以切线的方程为 ,
即.
切点坐标(1,1)
直线的点斜式方程
求曲线上点)处的切线方程:
(1)根据曲线的函数关系式求出切线斜率;
(2)将代入,求得曲线上点;
(3)根据直线的点斜式方程,得切线方程
【总结】
例 5.已知函数,求曲线在处的切线方程.
解:因为
,
又因为,
所以切线的方程为 ,
即.
求曲线在点(1,3)处的切线方程.
跟踪训练:
解:因为
,
又因为切点坐标为,
所以切线的方程为 ,
即.
探究点3:求函数近似值
f (x0) = .
当很小时,f (x0)
所以,当很小时,
.
以直代曲
例6 .已知函数,计算的近似值.
解:由题意可得,,,
因此
.
导数的几何意义
切线
导数的
几何意义
导数的
应用
切线斜率
求切线方程
