6.2.2导数与函数的极值、最值(二) 课件(共13张PPT) 2023-2024学年高二数学同步讲义(人教B版2019选择性必修第三册)
文档属性
| 名称 | 6.2.2导数与函数的极值、最值(二) 课件(共13张PPT) 2023-2024学年高二数学同步讲义(人教B版2019选择性必修第三册) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-05 15:58:55 | ||
图片预览



文档简介
(共13张PPT)
6.2.2 导数与函数的极值、最值(2)
喜马拉雅山脉是世界海拔最高的山脉,位于中国与尼泊尔之间,其主峰珠穆朗玛峰,海拔8844.43米,也是世界上最高的山峰!
吐鲁番盆地位于新疆维吾尔族自治区东部,是中国最低的洼地,盆底的艾丁湖湖面海拔-154.31米,是我国大陆的最低处.
在数学学习中,也有类似的情况.例如,函数的最值问题!函数的极值与最值有什么关系呢?
1.理解函数最值的定义 . (重点)
2.理解函数的最值与极值的关系. (难点)
3.会利用导数求函数的最值.(难点)
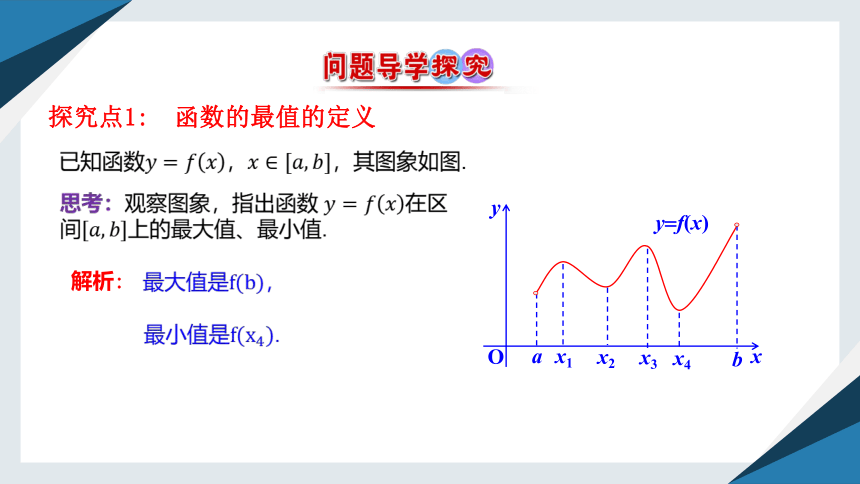
探究点1: 函数的最值的定义
已知函数,,其图象如图.
解析:
y
x
O
a
b
y=f(x)
x1
x2
x3
x4
思考:观察图象,指出函数 在区间上的最大值、最小值.
最小值是.
最大值是,
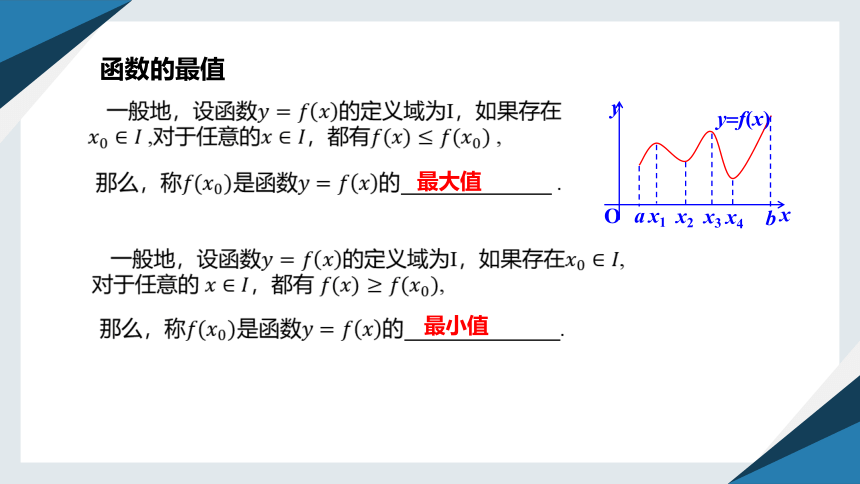
函数的最值
y
x
O
a
b
y=f(x)
x1
x2
x3
x4
一般地,设函数的定义域为I,如果存在 ,对于任意的,都有 ,
那么,称是函数的 .
一般地,设函数的定义域为I,如果存在,对于任意的 ,都有 ,
那么,称是函数的 .
最大值
最小值
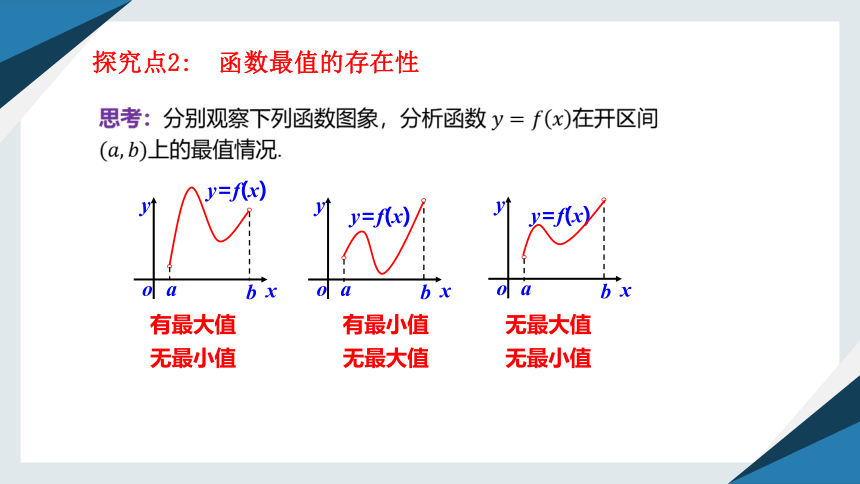
探究点2: 函数最值的存在性
思考:分别观察下列函数图象,分析函数 在开区间上的最值情况.
o
x
y
a
b
y=f(x)
o
x
y
a
b
y=f(x)
o
x
y
a
b
y=f(x)
有最大值
无最小值
有最小值
无最大值
无最大值
无最小值
函数最值存在性定理
一般地,如果函数 在闭区间上的图象是一条连续不断的曲线,
那么它在上必有 .
最大值与最小值
o
x
y
a
b
y=f(x)
探究点3: 可导函数的最值的求法
观察函数的图像,回忆函数最值的定义,回答下列问题:
思考1:图中所示函数的最值点与最值分别是多少?
x
y
y = f (x)
O
最大值点为2,最大值为3;
最小值点为0,最小值为-3.
最大值
最小值
思考2:图中所示函数的极值点与极值分别是多少?
极大值点为-2,极大值为2;
极小值点为0,极小值为-3.
思考3:一般的函数的最值与函数的极值有什么关系?怎样求可导函数的最值.
y
x
O
a
b
y=f(x)
x1
x2
x3
x4
① 一般地,如果函数的定义域内为且存在最值,函数在内可导,则函数的最值点一定是某个极值点;
②如果函数的定义域为且存在最值,函数在内可导,那么函数的最值点要么是区间端点或,要么是极值点.
利用导数求出区间内的极值,并与区间端点处函数值比较,即可确定.
例 1.已知,. 求的极值点以及极值、最值点以及最值.
解: .
解方程,可得或
解不等式,可得或此时递增,
解不等式可得此时递减.
因此, 在上递增,在上递减,在上递增
所以极大值为 ;极小值为.
由于端点值 ,
函数 的最大值点为1,最大值为 ,最小值点为0,
最小值为 0.
【总结】
求函数 在区间 上的最值的步骤如下:
求函数 在区间 上的极值;
2.将函数 的各极值与端点处的函数值 、 比较,
其中最大的一个是最大值,最小的一个是最小值.
解:
经比较可知在区间 上,
跟踪训练:
求函数在区间上的最值.
当变化时,与的变化情况如下表:
极大值4
极小值3
1.函数最值的定义.
2.求可导函数y=f (x)在闭区间[a,b]上的最值的步骤:
其中最大的一个为最大值,最小的一个为最小值.
(1)求f (x)在开区间(a,b)内所有使f′ (x)=0的点;
(2)计算函数f (x)在区间内使f′ (x)=0的所有点
和端点的函数值f (a)、 f (b);
本节课学习了哪些知识
6.2.2 导数与函数的极值、最值(2)
喜马拉雅山脉是世界海拔最高的山脉,位于中国与尼泊尔之间,其主峰珠穆朗玛峰,海拔8844.43米,也是世界上最高的山峰!
吐鲁番盆地位于新疆维吾尔族自治区东部,是中国最低的洼地,盆底的艾丁湖湖面海拔-154.31米,是我国大陆的最低处.
在数学学习中,也有类似的情况.例如,函数的最值问题!函数的极值与最值有什么关系呢?
1.理解函数最值的定义 . (重点)
2.理解函数的最值与极值的关系. (难点)
3.会利用导数求函数的最值.(难点)
探究点1: 函数的最值的定义
已知函数,,其图象如图.
解析:
y
x
O
a
b
y=f(x)
x1
x2
x3
x4
思考:观察图象,指出函数 在区间上的最大值、最小值.
最小值是.
最大值是,
函数的最值
y
x
O
a
b
y=f(x)
x1
x2
x3
x4
一般地,设函数的定义域为I,如果存在 ,对于任意的,都有 ,
那么,称是函数的 .
一般地,设函数的定义域为I,如果存在,对于任意的 ,都有 ,
那么,称是函数的 .
最大值
最小值
探究点2: 函数最值的存在性
思考:分别观察下列函数图象,分析函数 在开区间上的最值情况.
o
x
y
a
b
y=f(x)
o
x
y
a
b
y=f(x)
o
x
y
a
b
y=f(x)
有最大值
无最小值
有最小值
无最大值
无最大值
无最小值
函数最值存在性定理
一般地,如果函数 在闭区间上的图象是一条连续不断的曲线,
那么它在上必有 .
最大值与最小值
o
x
y
a
b
y=f(x)
探究点3: 可导函数的最值的求法
观察函数的图像,回忆函数最值的定义,回答下列问题:
思考1:图中所示函数的最值点与最值分别是多少?
x
y
y = f (x)
O
最大值点为2,最大值为3;
最小值点为0,最小值为-3.
最大值
最小值
思考2:图中所示函数的极值点与极值分别是多少?
极大值点为-2,极大值为2;
极小值点为0,极小值为-3.
思考3:一般的函数的最值与函数的极值有什么关系?怎样求可导函数的最值.
y
x
O
a
b
y=f(x)
x1
x2
x3
x4
① 一般地,如果函数的定义域内为且存在最值,函数在内可导,则函数的最值点一定是某个极值点;
②如果函数的定义域为且存在最值,函数在内可导,那么函数的最值点要么是区间端点或,要么是极值点.
利用导数求出区间内的极值,并与区间端点处函数值比较,即可确定.
例 1.已知,. 求的极值点以及极值、最值点以及最值.
解: .
解方程,可得或
解不等式,可得或此时递增,
解不等式可得此时递减.
因此, 在上递增,在上递减,在上递增
所以极大值为 ;极小值为.
由于端点值 ,
函数 的最大值点为1,最大值为 ,最小值点为0,
最小值为 0.
【总结】
求函数 在区间 上的最值的步骤如下:
求函数 在区间 上的极值;
2.将函数 的各极值与端点处的函数值 、 比较,
其中最大的一个是最大值,最小的一个是最小值.
解:
经比较可知在区间 上,
跟踪训练:
求函数在区间上的最值.
当变化时,与的变化情况如下表:
极大值4
极小值3
1.函数最值的定义.
2.求可导函数y=f (x)在闭区间[a,b]上的最值的步骤:
其中最大的一个为最大值,最小的一个为最小值.
(1)求f (x)在开区间(a,b)内所有使f′ (x)=0的点;
(2)计算函数f (x)在区间内使f′ (x)=0的所有点
和端点的函数值f (a)、 f (b);
本节课学习了哪些知识
