6.3利用导数解决实际问题 课件(共14张PPT)2023-2024学年高二数学同步讲义(人教B版2019选择性必修第三册)
文档属性
| 名称 | 6.3利用导数解决实际问题 课件(共14张PPT)2023-2024学年高二数学同步讲义(人教B版2019选择性必修第三册) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-05 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
6.3 利用导数解决实际问题
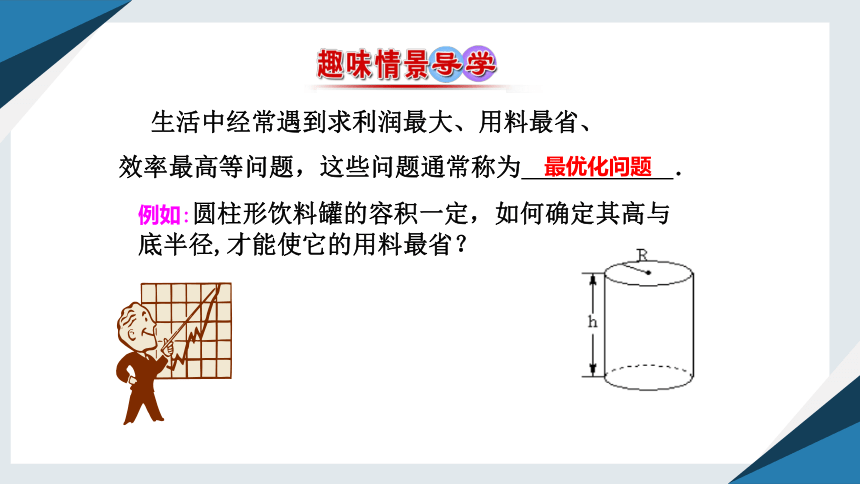
生活中经常遇到求利润最大、用料最省、
效率最高等问题,这些问题通常称为 .
最优化问题
例如:圆柱形饮料罐的容积一定,如何确定其高与底半径,才能使它的用料最省?
1.理解导数在解决实际问题中的作用. (重点)
2.能利用导数知识解决实际中的最优化问题. (难点)
3.将实际问题转化为数学问题,建立函数模型.
(难点)
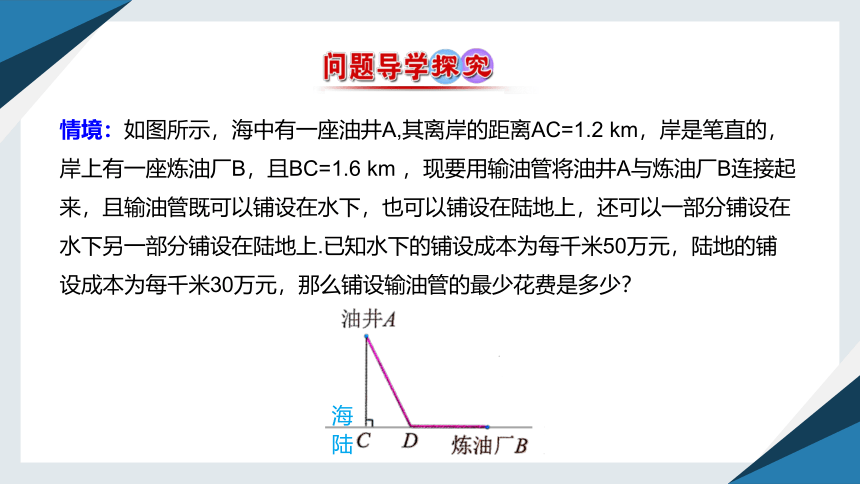
情境:如图所示,海中有一座油井A,其离岸的距离AC=1.2 km,岸是笔直的,岸上有一座炼油厂B,且BC=1.6 km ,现要用输油管将油井A与炼油厂B连接起来,且输油管既可以铺设在水下,也可以铺设在陆地上,还可以一部分铺设在水下另一部分铺设在陆地上.已知水下的铺设成本为每千米50万元,陆地的铺设成本为每千米30万元,那么铺设输油管的最少花费是多少?
海
陆
思考:分别计算下列两种算法的铺设成本.
(1)先沿AC铺设,再沿CB铺设;
(2)直接沿着线段AB铺设.
海
陆
解:(1) 成本为万元.
(2)
所以直接沿线段AB铺设,成本为 2×50=100万元.
还有其他方案吗?
在岸上取一点D,设其距离C的距离为,则
,
.
设先沿AD铺设再沿DB铺设输油管时成本为万元,
则1.6
因此,当 时,
海
陆
令 可解得
可知在上递减,在上递增,从而在时取得最小值,而且最小值为
1.6
最少花费是96万元.
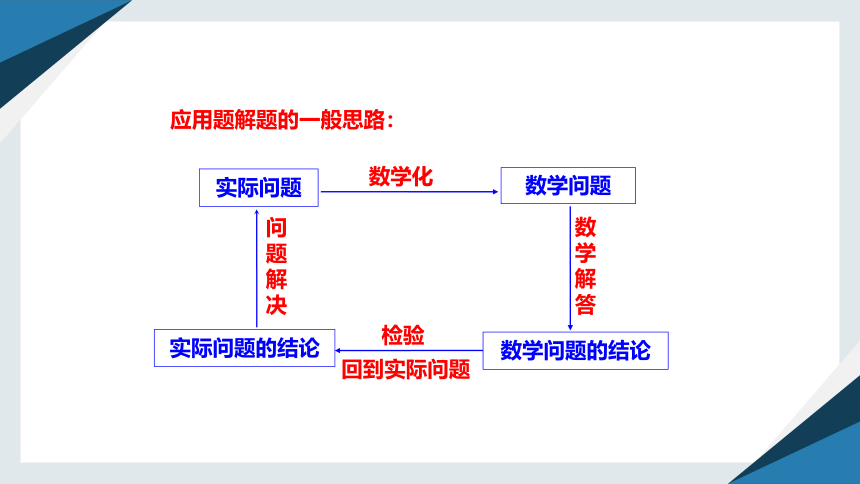
应用题解题的一般思路:
数学问题
实际问题
数学问题的结论
实际问题的结论
数
学
解
答
数学化
检验
回到实际问题
问
题
解
决
例 1.如图所示,某海岛码头O离岸边最近点B的距离是150 km,岸边的医药公司A与点B的距离为300km,现有一批药品要尽快送达海岛码头,已知A与B之间有一条公路,现要用海陆联运的方式运送这批药品,若汽车的时速为130km,快艇时速为50km. 试在岸边选一点C,先将药品用汽车从A送到C,再用快艇从C运到海岛码头,则点C选在何处可使运输时间最短?
解:设点C与点B的距离为km,运输时间为T()h,则
.
因为 ,
令可解得.
因此可知在上递减,在上递增,
从而在最小值.
这就是说,点C选在离点B点为时可使运输时间最短.
例 2.如图所示,先有一块边长为1.2 m的正方形铁板,如果从铁板的四个角各截去一个边长相同的小正方形,然后做成一个长方形的无盖容器,则容器的容积V m3 立方是截下的小正方形边长x m的函数.
(1)写出函数解析式;
(2)为了使容器的容积最大,截去的小正方形边长应为多少?
解:(1)根据题意可知,容器底面的边长为(1.2m,高为m ,于是
又因为显然的长度必须小于原有正方形铁板的一半,因此,
所以.
解:(2)由题意有
.
令可解得
因此可知在上递增,在上递减,
故在时取得极大值,而且在此时取得最大值.
即截去的正方形边长为m时,容器的容积最大.
例 3.某种退烧药能够降低的温度R是血液中该药含量M的函数,而且
其中C是一个常数,试求这种退烧药在血液中的含量M为多少时,能够降低的温度最大.
解:因为
所以由可解得
因此可知在上递增,在上递减.
故R在时取得极大值,而且此时取得最大值.
例 4.已知某种工艺品总成本C元是产量Q件的函数,且
将Q看成能取区间[1, 30]内的每一个值,求月产量Q为多少时,才能使每件
产品的平均成本最低?最低平均成本为多少?
解:记平均成本为元,则
因为时,有 ,
令,可解得.
因此可知在[1, 10]上递减,在[10, 30]上递增,
从而在时取得极小值,而且在此时取得最小值
=
即当月产量为10件,每件产品的平均成本最低,最低为400元.
1.最优化问题.
2.应用题解题的一般思路:
数学问题
实际问题
数学问题的结论
实际问题的结论
数
学
解
答
数学化
检验
回到实际问题
问
题
解
决
本节课学习了哪些知识
6.3 利用导数解决实际问题
生活中经常遇到求利润最大、用料最省、
效率最高等问题,这些问题通常称为 .
最优化问题
例如:圆柱形饮料罐的容积一定,如何确定其高与底半径,才能使它的用料最省?
1.理解导数在解决实际问题中的作用. (重点)
2.能利用导数知识解决实际中的最优化问题. (难点)
3.将实际问题转化为数学问题,建立函数模型.
(难点)
情境:如图所示,海中有一座油井A,其离岸的距离AC=1.2 km,岸是笔直的,岸上有一座炼油厂B,且BC=1.6 km ,现要用输油管将油井A与炼油厂B连接起来,且输油管既可以铺设在水下,也可以铺设在陆地上,还可以一部分铺设在水下另一部分铺设在陆地上.已知水下的铺设成本为每千米50万元,陆地的铺设成本为每千米30万元,那么铺设输油管的最少花费是多少?
海
陆
思考:分别计算下列两种算法的铺设成本.
(1)先沿AC铺设,再沿CB铺设;
(2)直接沿着线段AB铺设.
海
陆
解:(1) 成本为万元.
(2)
所以直接沿线段AB铺设,成本为 2×50=100万元.
还有其他方案吗?
在岸上取一点D,设其距离C的距离为,则
,
.
设先沿AD铺设再沿DB铺设输油管时成本为万元,
则1.6
因此,当 时,
海
陆
令 可解得
可知在上递减,在上递增,从而在时取得最小值,而且最小值为
1.6
最少花费是96万元.
应用题解题的一般思路:
数学问题
实际问题
数学问题的结论
实际问题的结论
数
学
解
答
数学化
检验
回到实际问题
问
题
解
决
例 1.如图所示,某海岛码头O离岸边最近点B的距离是150 km,岸边的医药公司A与点B的距离为300km,现有一批药品要尽快送达海岛码头,已知A与B之间有一条公路,现要用海陆联运的方式运送这批药品,若汽车的时速为130km,快艇时速为50km. 试在岸边选一点C,先将药品用汽车从A送到C,再用快艇从C运到海岛码头,则点C选在何处可使运输时间最短?
解:设点C与点B的距离为km,运输时间为T()h,则
.
因为 ,
令可解得.
因此可知在上递减,在上递增,
从而在最小值.
这就是说,点C选在离点B点为时可使运输时间最短.
例 2.如图所示,先有一块边长为1.2 m的正方形铁板,如果从铁板的四个角各截去一个边长相同的小正方形,然后做成一个长方形的无盖容器,则容器的容积V m3 立方是截下的小正方形边长x m的函数.
(1)写出函数解析式;
(2)为了使容器的容积最大,截去的小正方形边长应为多少?
解:(1)根据题意可知,容器底面的边长为(1.2m,高为m ,于是
又因为显然的长度必须小于原有正方形铁板的一半,因此,
所以.
解:(2)由题意有
.
令可解得
因此可知在上递增,在上递减,
故在时取得极大值,而且在此时取得最大值.
即截去的正方形边长为m时,容器的容积最大.
例 3.某种退烧药能够降低的温度R是血液中该药含量M的函数,而且
其中C是一个常数,试求这种退烧药在血液中的含量M为多少时,能够降低的温度最大.
解:因为
所以由可解得
因此可知在上递增,在上递减.
故R在时取得极大值,而且此时取得最大值.
例 4.已知某种工艺品总成本C元是产量Q件的函数,且
将Q看成能取区间[1, 30]内的每一个值,求月产量Q为多少时,才能使每件
产品的平均成本最低?最低平均成本为多少?
解:记平均成本为元,则
因为时,有 ,
令,可解得.
因此可知在[1, 10]上递减,在[10, 30]上递增,
从而在时取得极小值,而且在此时取得最小值
=
即当月产量为10件,每件产品的平均成本最低,最低为400元.
1.最优化问题.
2.应用题解题的一般思路:
数学问题
实际问题
数学问题的结论
实际问题的结论
数
学
解
答
数学化
检验
回到实际问题
问
题
解
决
本节课学习了哪些知识
