数学人教A版(2019)必修第一册5.6.2函数y=Asin(ωx+φ)的图象 课件(共34张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.6.2函数y=Asin(ωx+φ)的图象 课件(共34张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-04 14:21:59 | ||
图片预览









文档简介
(共34张PPT)
5.6.2 函数y=Asin(ωx +φ)的图象
用电脑动态演示函数图像的变换过程,让学生形象直观地看到各参数对图像的影响,从而发现和归纳出各种变换法则。
重 点
ZhongDian
难 点
Nan Dian
提出问题
1
研究问题
2
归纳问题
3
应用举例及练习
4
小结及作业
5
内容
Contents
提出问题
1
以抛出问题的形式展开教学,让学生带着问题开始有针对性地学习
Part
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
01
02
在同一坐标系中画出 和 靠近原点的一个周期内的图像,并观察它们与 的图像之间的关系。
在同一坐标系中画出 和 靠近原点的一个周期内的图像,并观察它们与 的图像之间的关系。
x
y
sin
=
在同一坐标系中画出 和 靠近原点的一个周期内的图像,并观察它们与 的图像之间的关系。
03
研究问题
2
对问题进行研究分析,探讨解决方案、解题思路
Part
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
画出函数:y=sin x
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
4
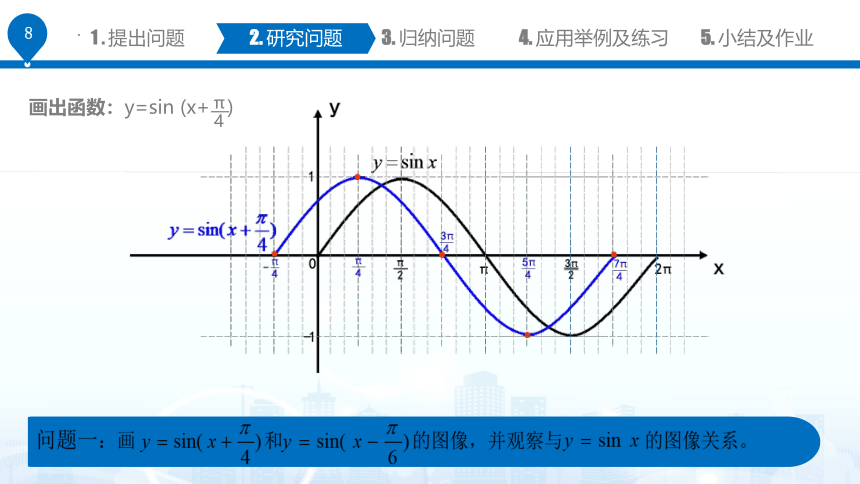
画出函数:y=sin (x+ )
—
π
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
6
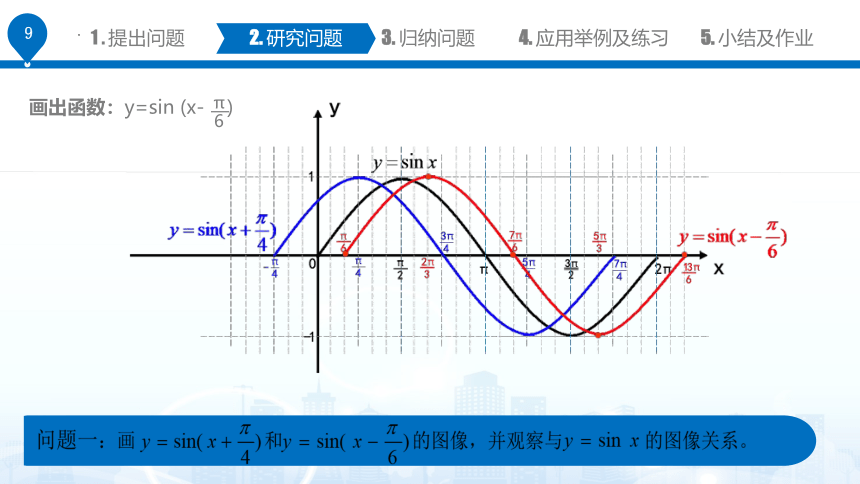
画出函数:y=sin (x- )
—
π
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
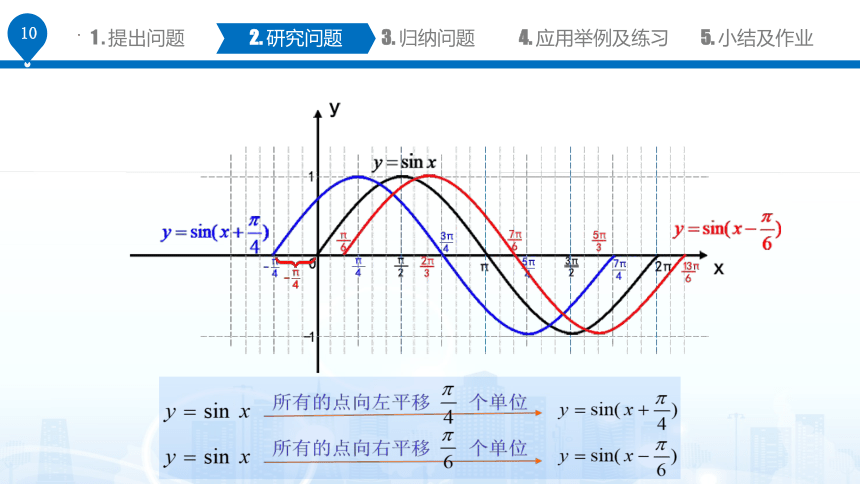
变式1:如何由 的图像变换得到 和 的图像?
1
-1
所有的点向左平移 个单位
所有的点向右平移 个单位
函数 的图像,可看作由函数 的图像上所有的点向左
或向右平移 个单位而得,注意 的正负决定平移方向, 决定平移大小。
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
变换法则(一)
)
0
(
>
w
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
问题二:画 和 的图像,并观察其与 的图像关系
1
-1
纵坐标不变,横坐标变为原来的 倍
纵坐标不变,横坐标变为原来的 倍
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
0<ω <1时,纵坐标不变,横坐标伸长到原来的1/ω倍
ω >1时,纵坐标不变,横坐标缩短到原来的1/ω倍
一般地,
可以看作由 上所有的点的纵坐标不
变,横坐标变为原来的 倍而得,注意 与1的大小决定是扩大还是缩小。
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
变式2:如何由 的图像变换得到 的图像?
-1
1
纵坐标不变,横坐标变为原来的 倍
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
函数 可以看作由 上所有的点的纵坐标不变,
横坐标变为原来的 倍而得,注意 与1的大小决定是扩大还是缩小。
变换法则(二)
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
问题三:画 和 的图像,并观察其与 的关系
横坐标不变,纵坐标变为原来的 倍
横坐标不变,纵坐标变为原来的 倍
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
可以看作由 上所有的点,横坐标不变,纵坐标
变为原来的A倍而得。注意 与1的大小决定是扩大还是缩小。
变换法则(三)
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
综合题:如何由 的图像变换到 的图像?
变换方式一:
向左平移 个单位
纵坐标不变,
横坐标变为原来的 倍
-1
1
向左平移 个单位
纵坐标不变,
横坐标变为原来的 倍
一般地:
>0时
-1
1
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
综合题:如何由 的图像变换到 的图像?
变换方式二:
纵坐标不变
横坐标变为原来的 倍
向左平移 个单位
一般地:
纵坐标不变,横坐标
变为原来的 倍
向左平移 个单位
> 0
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
变换法则(四)
由函数 的图像变换得到函数 的图像。
变换方式一:从参数 入手
向左平移 个单位
纵坐标不变,
横坐标变为原来的 倍
>0时
变换方式二:从参数 入手
纵坐标不变,
横坐标变为原来的 倍
向左平移 个 单 位
> 0
归纳问题
3
对问题的解答思路进行归纳
Part
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
变换一:从参数 入手
变换二:从参数 入手
变换三:从参数A入手
(xx同学,由你来口述)
由函数 的图像变换得到函数 的图像。
向左平移
个单位
纵坐标不变,横坐标变为原来的 倍
横坐标不变,纵坐标伸长到原来的A倍
向左平移 个 单 位
纵坐标不变,横坐标
变为原来的 倍
应用举例及练习
4
利用例题的解答练习来加深记忆,强化其吸收
Part
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
例1、若将某函数的图像向右平移 以后得到的图像的函数解析式是 ,则原来的函数解析式是( )。
A.
B.
C.
D.
A
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
例2、为了得到函数 的图像,只需将函数 的图像上的每个点( )。
A.横坐标伸长为原来的2倍,纵坐标不变;
C.纵坐标伸长为原来的2倍,横坐标不变;
D.纵坐标伸长为原来的 倍,横坐标不变。
B.横坐标伸长为原来的 倍,纵坐标不变;
A
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
例3:若函数 图像上每一个点的纵坐标不变,横
坐标伸长到原来的3倍得到函数 的图像,再将图像上所有的点向右
平移 个单位得到 的图像,最后将图像上每一点的横坐标不变,
纵坐标伸长到原来的3倍得到 的图像
则 的解析式为
小结与作业
5
对当节教学内容进行归纳总结,并布置课后作业加强记忆、巩固学习成果
Part
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
1.变换法则
>0时,向左平行移动 个单位
<0时,向右平行移动 个单位
)
0
(
>
w
< 0 ,向右平移 | |个单位
>0 ,向左平移 个单位
<1>水平平移变换 (φ值有变化)
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
1.变换法则
A>1时,横坐标不变,纵坐标伸长到原来的A倍
0<2>上下伸缩变换 (A值有变化)
0<ω <1时,纵坐标不变,横坐标伸长到原来的1/ω倍
ω >1时,纵坐标不变,横坐标缩短到原来的1/ω倍
<3>水平伸缩变换 (ω值有变化)
纵坐标不变,横坐标变为原来的1/ω 倍
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
2.题型解析
函数变换前解析式,变换后解析式及变换法则三者知其二能求第三。
注意:两函数名相同,变换方向要明确。
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
2、若 , 呢?
1、要得到函数 的图像,需将函数 怎样变换?
3.拓展自学
4.课后作业
P55. T2、T3
谢
谢
大
家
5.6.2 函数y=Asin(ωx +φ)的图象
用电脑动态演示函数图像的变换过程,让学生形象直观地看到各参数对图像的影响,从而发现和归纳出各种变换法则。
重 点
ZhongDian
难 点
Nan Dian
提出问题
1
研究问题
2
归纳问题
3
应用举例及练习
4
小结及作业
5
内容
Contents
提出问题
1
以抛出问题的形式展开教学,让学生带着问题开始有针对性地学习
Part
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
01
02
在同一坐标系中画出 和 靠近原点的一个周期内的图像,并观察它们与 的图像之间的关系。
在同一坐标系中画出 和 靠近原点的一个周期内的图像,并观察它们与 的图像之间的关系。
x
y
sin
=
在同一坐标系中画出 和 靠近原点的一个周期内的图像,并观察它们与 的图像之间的关系。
03
研究问题
2
对问题进行研究分析,探讨解决方案、解题思路
Part
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
画出函数:y=sin x
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
4
画出函数:y=sin (x+ )
—
π
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
6
画出函数:y=sin (x- )
—
π
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
变式1:如何由 的图像变换得到 和 的图像?
1
-1
所有的点向左平移 个单位
所有的点向右平移 个单位
函数 的图像,可看作由函数 的图像上所有的点向左
或向右平移 个单位而得,注意 的正负决定平移方向, 决定平移大小。
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
变换法则(一)
)
0
(
>
w
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
问题二:画 和 的图像,并观察其与 的图像关系
1
-1
纵坐标不变,横坐标变为原来的 倍
纵坐标不变,横坐标变为原来的 倍
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
0<ω <1时,纵坐标不变,横坐标伸长到原来的1/ω倍
ω >1时,纵坐标不变,横坐标缩短到原来的1/ω倍
一般地,
可以看作由 上所有的点的纵坐标不
变,横坐标变为原来的 倍而得,注意 与1的大小决定是扩大还是缩小。
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
变式2:如何由 的图像变换得到 的图像?
-1
1
纵坐标不变,横坐标变为原来的 倍
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
函数 可以看作由 上所有的点的纵坐标不变,
横坐标变为原来的 倍而得,注意 与1的大小决定是扩大还是缩小。
变换法则(二)
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
问题三:画 和 的图像,并观察其与 的关系
横坐标不变,纵坐标变为原来的 倍
横坐标不变,纵坐标变为原来的 倍
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
可以看作由 上所有的点,横坐标不变,纵坐标
变为原来的A倍而得。注意 与1的大小决定是扩大还是缩小。
变换法则(三)
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
综合题:如何由 的图像变换到 的图像?
变换方式一:
向左平移 个单位
纵坐标不变,
横坐标变为原来的 倍
-1
1
向左平移 个单位
纵坐标不变,
横坐标变为原来的 倍
一般地:
>0时
-1
1
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
综合题:如何由 的图像变换到 的图像?
变换方式二:
纵坐标不变
横坐标变为原来的 倍
向左平移 个单位
一般地:
纵坐标不变,横坐标
变为原来的 倍
向左平移 个单位
> 0
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
变换法则(四)
由函数 的图像变换得到函数 的图像。
变换方式一:从参数 入手
向左平移 个单位
纵坐标不变,
横坐标变为原来的 倍
>0时
变换方式二:从参数 入手
纵坐标不变,
横坐标变为原来的 倍
向左平移 个 单 位
> 0
归纳问题
3
对问题的解答思路进行归纳
Part
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
变换一:从参数 入手
变换二:从参数 入手
变换三:从参数A入手
(xx同学,由你来口述)
由函数 的图像变换得到函数 的图像。
向左平移
个单位
纵坐标不变,横坐标变为原来的 倍
横坐标不变,纵坐标伸长到原来的A倍
向左平移 个 单 位
纵坐标不变,横坐标
变为原来的 倍
应用举例及练习
4
利用例题的解答练习来加深记忆,强化其吸收
Part
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
例1、若将某函数的图像向右平移 以后得到的图像的函数解析式是 ,则原来的函数解析式是( )。
A.
B.
C.
D.
A
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
例2、为了得到函数 的图像,只需将函数 的图像上的每个点( )。
A.横坐标伸长为原来的2倍,纵坐标不变;
C.纵坐标伸长为原来的2倍,横坐标不变;
D.纵坐标伸长为原来的 倍,横坐标不变。
B.横坐标伸长为原来的 倍,纵坐标不变;
A
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
例3:若函数 图像上每一个点的纵坐标不变,横
坐标伸长到原来的3倍得到函数 的图像,再将图像上所有的点向右
平移 个单位得到 的图像,最后将图像上每一点的横坐标不变,
纵坐标伸长到原来的3倍得到 的图像
则 的解析式为
小结与作业
5
对当节教学内容进行归纳总结,并布置课后作业加强记忆、巩固学习成果
Part
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
1.变换法则
>0时,向左平行移动 个单位
<0时,向右平行移动 个单位
)
0
(
>
w
< 0 ,向右平移 | |个单位
>0 ,向左平移 个单位
<1>水平平移变换 (φ值有变化)
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
1.变换法则
A>1时,横坐标不变,纵坐标伸长到原来的A倍
0
0<ω <1时,纵坐标不变,横坐标伸长到原来的1/ω倍
ω >1时,纵坐标不变,横坐标缩短到原来的1/ω倍
<3>水平伸缩变换 (ω值有变化)
纵坐标不变,横坐标变为原来的1/ω 倍
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
2.题型解析
函数变换前解析式,变换后解析式及变换法则三者知其二能求第三。
注意:两函数名相同,变换方向要明确。
1 . 提出问题
2. 研究问题
3. 归纳问题
4. 应用举例及练习
5. 小结及作业
2、若 , 呢?
1、要得到函数 的图像,需将函数 怎样变换?
3.拓展自学
4.课后作业
P55. T2、T3
谢
谢
大
家
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
