六年级上册数学苏教版长方体和正方体(课件)(共22张PPT)
文档属性
| 名称 | 六年级上册数学苏教版长方体和正方体(课件)(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-04 07:12:25 | ||
图片预览







文档简介
(共22张PPT)
等式与方程
长方体和正方体
苏教版数学六年级上册
1.两个面相交的线叫作棱,三条棱相交的点叫作顶点。
长方体的概念
2.长方体有几条棱和几个顶点?它的面和棱各有什么特点?
正方体的概念
3.长方体相交于同一顶点的三条棱的长度,分别叫作长、宽和高。
4.正方体有几条棱、几个顶点和几个面?
正方体的概念
5.正方体是特殊的长方体
正方体的概念
拿一个长方体纸盒,沿着一条棱剪开,看看它的展开图
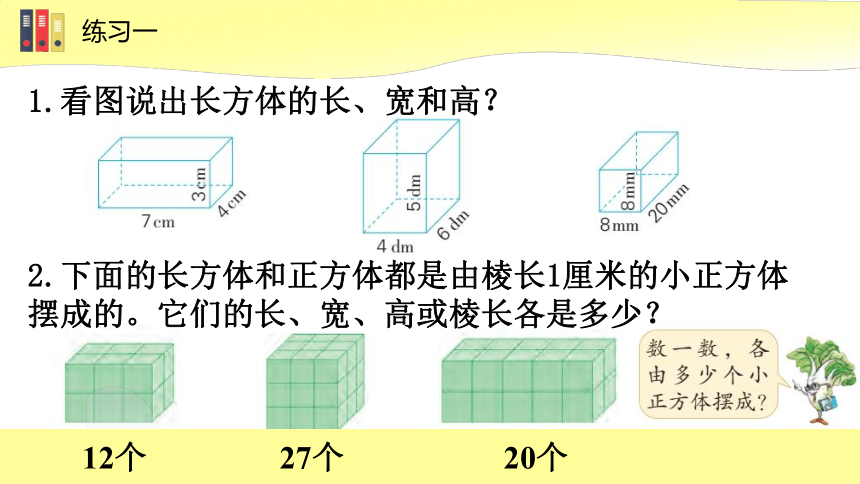
练习一
1.看图说出长方体的长、宽和高?
2.下面的长方体和正方体都是由棱长1厘米的小正方体摆成的。它们的长、宽、高或棱长各是多少?
12个
27个
20个
正方体的概念
做一个长6厘米、宽5厘米、高4厘米的长方体纸盒,至少用硬纸板多少平方厘米?
2×﹙6×5+6×4+4×5﹚=148cm2
正方体的概念
做一个棱长3分米的正方体纸盒,至少要用硬纸板多少平方分米?
6×﹙3×3﹚=54dm2
长方体(或正方体)6个面的总面积,叫作它的表面积。
正方体的概念
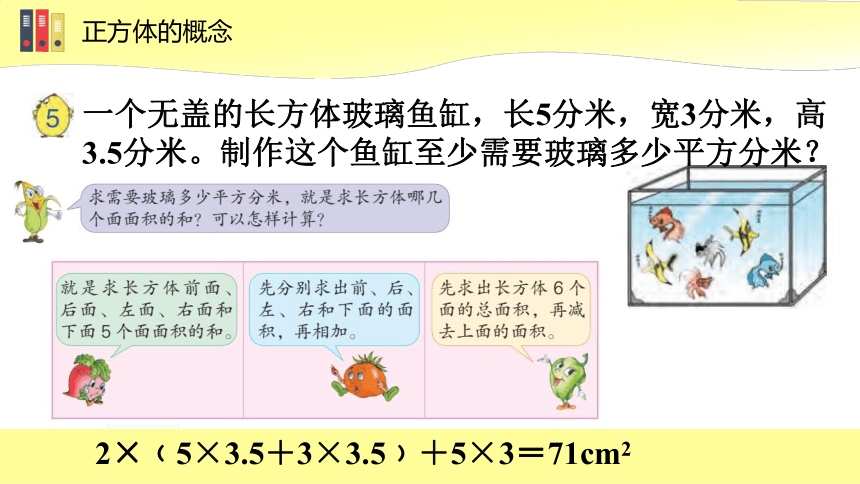
一个无盖的长方体玻璃鱼缸,长5分米,宽3分米,高3.5分米。制作这个鱼缸至少需要玻璃多少平方分米?
2×﹙5×3.5+3×3.5﹚+5×3=71cm2
练习二
1.一个用硬纸板做成的长方体影集封套,长3l厘米,宽27厘米,高2.5厘米,封套的左面不封口。做这个封套至少需要多少平方厘米硬纸板?
2×﹙31×27+27×2.5﹚+31×2.5
=1886.5cm2
2.学校生物小组做了一个昆虫箱。昆虫箱的上、下、左、右面是木板,前、后两面装蝇纱网。至少需要多少平方厘米木板和纱网?
木板: 2×﹙35×25+40×25﹚=3750cm2
纱网: 2×40×35=2800cm2
练习二
下图表示用棱长1厘米的正方体摆成的物体。
(1)从前面、上面和右面看到的分别是什么形状?
试着画一画。
(2)这个物体的表面积是多少平方厘米?
(3)如果添加同样的正方体,把这个物体补成
大正方体,表面积至少是多少平方厘米?
长方体和正方体
两个同样大的玻璃杯,左边盛满水,右边放一个桃。
想一想:在两个同样大的玻璃杯里分别放一个桃和一个荔枝,再往这两个杯里到满水。倒进几号杯的水多一些?为什么?
同样,下面三个水果,哪一个占的空间大?想一想,如果把它们放在同样大的杯中,再倒满水,哪个杯里水占的空间大?
物体所占空间的大小叫作物体的体积。
长方体和正方体
长方体和正方体
容器所能容纳物体的体积叫作容器的容积。
把大小两块石子分别放入两个装满水的同样大的杯子里。
长方体和正方体
下面的长方体和正方体,哪个体积大?
为了准确测量或计量体积的大小,需要统一体积单位。常用的体积单位有立方厘米、立方分米和立方米,也可以写成cm3、dm3和m3。同时,1dm3=1L;1cm3=1ml
练习三
1.商店把同样的盒装饼干摆成3堆,这三堆饼干的体积相等吗?为什么?
2.学校自然实验室买来两箱仪器,从外面看两个箱子同样大。
体积一样大,容积不一样。
体积一样大
长方体和正方体
右图中的长方体是用1立方厘米的小正方体摆成的。它的长、宽、高各是多少厘米?摆这个长方体用了多少个1立方厘米的小正方体?长方体的体积是多少立方厘米?
长3cm,宽2cm,高2cm; 12个;3×2×2=12
用1立方厘米的小正方体摆出下面的长方体,各需要多少个?
4个
12个
24个
长方体的体积=长×宽×高 即:V=a×b×h
练习三
正方体的体积=棱长×棱长×棱长 即:V=a×a×a
计算下面长方体和正方体纸盒的体积
V=12×12×12=1728cm3
V=30×10×8=2400cm3
长方体和正方体底面的面积,叫作它们的底面积。
长方体(或正方体)的体积=底面积×高 即:V=S×h
长方体和正方体
练习四
1.幼儿园有一排长方体的储物柜,共占地0.84平方米,储物柜高0.75米。这排储物柜所占的空间是多少立方米?
V=S×h=0.84×0.75=0.63m3
2.工人把10.5立方米黄沙铺在一个长6米、宽3.5米的长方体沙坑里,可以铺多厚?(用方程解)
本课小结
1. 什么是棱、顶点?
2. 长方体和正方体分别有几个面、几个棱和几个顶点?
4. 长方体和正方体的展开图?
3. 长方体和正方体的关系。
5. 长方体和正方体的表面积公式分别为?
6. 长方体和正方体的体积公式分别为?
本课小结
本节课程结束
谢谢听讲
等式与方程
长方体和正方体
苏教版数学六年级上册
1.两个面相交的线叫作棱,三条棱相交的点叫作顶点。
长方体的概念
2.长方体有几条棱和几个顶点?它的面和棱各有什么特点?
正方体的概念
3.长方体相交于同一顶点的三条棱的长度,分别叫作长、宽和高。
4.正方体有几条棱、几个顶点和几个面?
正方体的概念
5.正方体是特殊的长方体
正方体的概念
拿一个长方体纸盒,沿着一条棱剪开,看看它的展开图
练习一
1.看图说出长方体的长、宽和高?
2.下面的长方体和正方体都是由棱长1厘米的小正方体摆成的。它们的长、宽、高或棱长各是多少?
12个
27个
20个
正方体的概念
做一个长6厘米、宽5厘米、高4厘米的长方体纸盒,至少用硬纸板多少平方厘米?
2×﹙6×5+6×4+4×5﹚=148cm2
正方体的概念
做一个棱长3分米的正方体纸盒,至少要用硬纸板多少平方分米?
6×﹙3×3﹚=54dm2
长方体(或正方体)6个面的总面积,叫作它的表面积。
正方体的概念
一个无盖的长方体玻璃鱼缸,长5分米,宽3分米,高3.5分米。制作这个鱼缸至少需要玻璃多少平方分米?
2×﹙5×3.5+3×3.5﹚+5×3=71cm2
练习二
1.一个用硬纸板做成的长方体影集封套,长3l厘米,宽27厘米,高2.5厘米,封套的左面不封口。做这个封套至少需要多少平方厘米硬纸板?
2×﹙31×27+27×2.5﹚+31×2.5
=1886.5cm2
2.学校生物小组做了一个昆虫箱。昆虫箱的上、下、左、右面是木板,前、后两面装蝇纱网。至少需要多少平方厘米木板和纱网?
木板: 2×﹙35×25+40×25﹚=3750cm2
纱网: 2×40×35=2800cm2
练习二
下图表示用棱长1厘米的正方体摆成的物体。
(1)从前面、上面和右面看到的分别是什么形状?
试着画一画。
(2)这个物体的表面积是多少平方厘米?
(3)如果添加同样的正方体,把这个物体补成
大正方体,表面积至少是多少平方厘米?
长方体和正方体
两个同样大的玻璃杯,左边盛满水,右边放一个桃。
想一想:在两个同样大的玻璃杯里分别放一个桃和一个荔枝,再往这两个杯里到满水。倒进几号杯的水多一些?为什么?
同样,下面三个水果,哪一个占的空间大?想一想,如果把它们放在同样大的杯中,再倒满水,哪个杯里水占的空间大?
物体所占空间的大小叫作物体的体积。
长方体和正方体
长方体和正方体
容器所能容纳物体的体积叫作容器的容积。
把大小两块石子分别放入两个装满水的同样大的杯子里。
长方体和正方体
下面的长方体和正方体,哪个体积大?
为了准确测量或计量体积的大小,需要统一体积单位。常用的体积单位有立方厘米、立方分米和立方米,也可以写成cm3、dm3和m3。同时,1dm3=1L;1cm3=1ml
练习三
1.商店把同样的盒装饼干摆成3堆,这三堆饼干的体积相等吗?为什么?
2.学校自然实验室买来两箱仪器,从外面看两个箱子同样大。
体积一样大,容积不一样。
体积一样大
长方体和正方体
右图中的长方体是用1立方厘米的小正方体摆成的。它的长、宽、高各是多少厘米?摆这个长方体用了多少个1立方厘米的小正方体?长方体的体积是多少立方厘米?
长3cm,宽2cm,高2cm; 12个;3×2×2=12
用1立方厘米的小正方体摆出下面的长方体,各需要多少个?
4个
12个
24个
长方体的体积=长×宽×高 即:V=a×b×h
练习三
正方体的体积=棱长×棱长×棱长 即:V=a×a×a
计算下面长方体和正方体纸盒的体积
V=12×12×12=1728cm3
V=30×10×8=2400cm3
长方体和正方体底面的面积,叫作它们的底面积。
长方体(或正方体)的体积=底面积×高 即:V=S×h
长方体和正方体
练习四
1.幼儿园有一排长方体的储物柜,共占地0.84平方米,储物柜高0.75米。这排储物柜所占的空间是多少立方米?
V=S×h=0.84×0.75=0.63m3
2.工人把10.5立方米黄沙铺在一个长6米、宽3.5米的长方体沙坑里,可以铺多厚?(用方程解)
本课小结
1. 什么是棱、顶点?
2. 长方体和正方体分别有几个面、几个棱和几个顶点?
4. 长方体和正方体的展开图?
3. 长方体和正方体的关系。
5. 长方体和正方体的表面积公式分别为?
6. 长方体和正方体的体积公式分别为?
本课小结
本节课程结束
谢谢听讲
