北师大版六年级下册数学《《总复习——数的认识》课件(共18张PPT)
文档属性
| 名称 | 北师大版六年级下册数学《《总复习——数的认识》课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 187.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-04 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
北师大六年级下册总复习
数的认识(三)
根据这两道算式,你能说一说哪个数是哪个数的倍数,
哪个数是哪个数的因数吗?
根据是不是2的倍数来分,自然数可以分为哪两类?
2的倍数有什么特征?
5的倍数有什么特征?
3的倍数有什么特征?
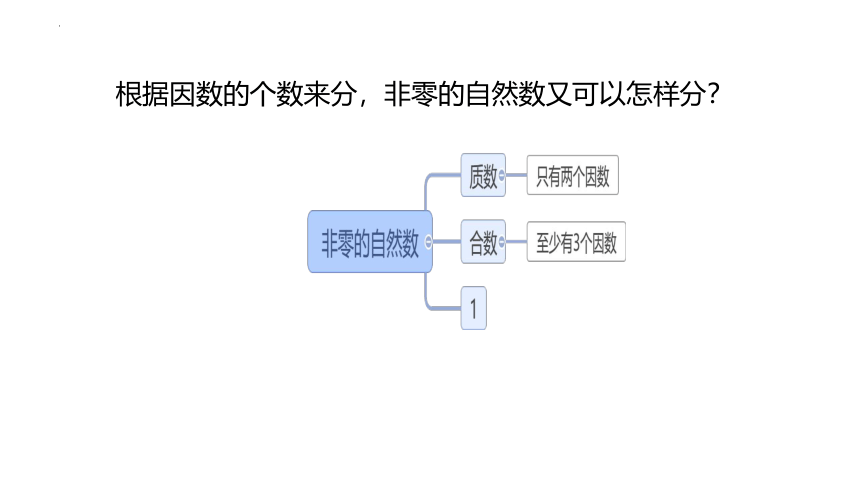
根据因数的个数来分,非零的自然数又可以怎样分?
6的倍数有哪些?
一个数的倍数的个数是( ),最小的倍数是( ),
( )最大的倍数。
20的因数有哪些?
一个数的因数的个数是( ),最小的因数是( ),最大的因数是( )。
无限的
本身
没有
有限的
1
本身
什么叫两个数最大公因数
什么叫两个数的最小公倍数?
求下面各组数的最大公因数和最小公倍数
12和8 7和11 12和36
当两个数是互质关系时,它们的最大公因数是( ),
它们的最小公倍数是( )。
当两个数是倍数关系是,它们的最大公因数是( ),
它们的最小公倍数是( )。
1
它们的积
小数
大数
4、一个数各个数位上的数字加起来的和是9的倍数,那么这个数也是( )的倍数。如果要让□729成为3的倍数,那么□里可以填( )。
填空
102
96
1,2,3,4,6,9,12,18,36
1,2,3,4,6,8,12,24
1,2,3,4,6,12
11
13
15
3
3或6或9
1、是2、3的倍数最小的三位数是( ),最大的两位数是( )。
2、36的全部因数有( ),24的因数有( ),( )既是24的因数又是36的因数。
3、3个连续奇数的和是39,这三个连续的奇数是( )、( )和( )。
填空
8、有一个两位数,它是2的倍数,同时,它的各个数位上的数字的积是12,这个两位数可能是( )。
5、写出1~20的所有质数是( ),1~20中( )既是合数又是奇数,在1~20中,共有( )个合数。( )既不是质数,也不是合数。
6、有一个比14大,比19小的奇数,它同时是质数,这个数是( )。
7、215至少减去( )就是3的倍数;174至少加上( )就是2和5的倍数。
2,3,5,7,11,13,17,19
9,15
11
1
17
2
6
26或62或34
10、m与n是相邻的自然数(0除外),它们的最大公因数是( ),最小公倍数是( )。m÷n=9,m与n的最大公因数是( ),最小公倍数是( )。
填空
9、( )既是24的因数又是6的倍数。
6;12;24
1
mn
n
m
1、一个数的最大因数是18,另一个数的最小倍数是24,它们的最大公因数和最小公倍数分别是( )。
A、2,36 B、 6,72 C、3,48
选择
B
选择
2、要使4□6是3的倍数,□里可以填( )
A、1、2、3
B、2、4、6
C、2、5、8
C
3、如果a÷b=9,那么( )
A、a一定能被b整除
B、a一定能被b除尽
C、b一定是a的约数
选择
B
1、用24个边长1厘米的小正方形可以拼成不同的长方形,一共有几种拼法?这个长方形的长可以是多少?
应用题
答一共有4种拼法。这个长方形的长可以①是24厘米;②是12厘米; 是8厘米;④是6厘米。
③
24的因数有1,2,3,4,6,8,12,24.
2、五一班刘老师指导60人分组做游戏,要求每组人数相等,且每组不多于15人,不少于8人,有几种分法?
应用题
60的因数有:1,2,3,4,5,6,10,12,15,
20,30,60.
答有3种,每组10人,有6组;每组12人,有5组;
每组15人,有4组。
应用题
3、有两根绳子,长度分别是28米和35米,要把它们截成同样长的小段,没有剩余,每段绳子最长是几米?一共可以截成几段?
28的因数有:1,2,4,7,14,28.
35的因数有:1,5,7,35.
35+28=63(米)63 7=9(段)
答:每段绳子最长是7米,一共可以截取9段。
4、五年级三班分学习小组,每组6人、每组8人、或每组12人,都正好分完,这个班学生接近50人,你知道五年级三班有多少学生吗?
应用题
50以内6的倍数有:6,12,18,24,30,36,42,48
50以内8的倍数有:8,16,24,32,40,48
50以内12的倍数有:12,24,36,48
答五年级三班有48人。
应用题
用 三张数字卡片按要求摆数
1)任意取两张数字卡片,可以摆出的2的倍数有( );可以摆出3的倍数有( );可以摆出的5的倍数有( )。
2
5
7
2)任意取;两张卡片摆出的数中,既有因数3又有因数5的数有( )。
3)摆出的所有三位数中,最大的是( ),最小的是( )。
52,72
72,27,57,75
25,75
75
752
257
通过本节课的复习,
你有什么收获?
北师大六年级下册总复习
数的认识(三)
根据这两道算式,你能说一说哪个数是哪个数的倍数,
哪个数是哪个数的因数吗?
根据是不是2的倍数来分,自然数可以分为哪两类?
2的倍数有什么特征?
5的倍数有什么特征?
3的倍数有什么特征?
根据因数的个数来分,非零的自然数又可以怎样分?
6的倍数有哪些?
一个数的倍数的个数是( ),最小的倍数是( ),
( )最大的倍数。
20的因数有哪些?
一个数的因数的个数是( ),最小的因数是( ),最大的因数是( )。
无限的
本身
没有
有限的
1
本身
什么叫两个数最大公因数
什么叫两个数的最小公倍数?
求下面各组数的最大公因数和最小公倍数
12和8 7和11 12和36
当两个数是互质关系时,它们的最大公因数是( ),
它们的最小公倍数是( )。
当两个数是倍数关系是,它们的最大公因数是( ),
它们的最小公倍数是( )。
1
它们的积
小数
大数
4、一个数各个数位上的数字加起来的和是9的倍数,那么这个数也是( )的倍数。如果要让□729成为3的倍数,那么□里可以填( )。
填空
102
96
1,2,3,4,6,9,12,18,36
1,2,3,4,6,8,12,24
1,2,3,4,6,12
11
13
15
3
3或6或9
1、是2、3的倍数最小的三位数是( ),最大的两位数是( )。
2、36的全部因数有( ),24的因数有( ),( )既是24的因数又是36的因数。
3、3个连续奇数的和是39,这三个连续的奇数是( )、( )和( )。
填空
8、有一个两位数,它是2的倍数,同时,它的各个数位上的数字的积是12,这个两位数可能是( )。
5、写出1~20的所有质数是( ),1~20中( )既是合数又是奇数,在1~20中,共有( )个合数。( )既不是质数,也不是合数。
6、有一个比14大,比19小的奇数,它同时是质数,这个数是( )。
7、215至少减去( )就是3的倍数;174至少加上( )就是2和5的倍数。
2,3,5,7,11,13,17,19
9,15
11
1
17
2
6
26或62或34
10、m与n是相邻的自然数(0除外),它们的最大公因数是( ),最小公倍数是( )。m÷n=9,m与n的最大公因数是( ),最小公倍数是( )。
填空
9、( )既是24的因数又是6的倍数。
6;12;24
1
mn
n
m
1、一个数的最大因数是18,另一个数的最小倍数是24,它们的最大公因数和最小公倍数分别是( )。
A、2,36 B、 6,72 C、3,48
选择
B
选择
2、要使4□6是3的倍数,□里可以填( )
A、1、2、3
B、2、4、6
C、2、5、8
C
3、如果a÷b=9,那么( )
A、a一定能被b整除
B、a一定能被b除尽
C、b一定是a的约数
选择
B
1、用24个边长1厘米的小正方形可以拼成不同的长方形,一共有几种拼法?这个长方形的长可以是多少?
应用题
答一共有4种拼法。这个长方形的长可以①是24厘米;②是12厘米; 是8厘米;④是6厘米。
③
24的因数有1,2,3,4,6,8,12,24.
2、五一班刘老师指导60人分组做游戏,要求每组人数相等,且每组不多于15人,不少于8人,有几种分法?
应用题
60的因数有:1,2,3,4,5,6,10,12,15,
20,30,60.
答有3种,每组10人,有6组;每组12人,有5组;
每组15人,有4组。
应用题
3、有两根绳子,长度分别是28米和35米,要把它们截成同样长的小段,没有剩余,每段绳子最长是几米?一共可以截成几段?
28的因数有:1,2,4,7,14,28.
35的因数有:1,5,7,35.
35+28=63(米)63 7=9(段)
答:每段绳子最长是7米,一共可以截取9段。
4、五年级三班分学习小组,每组6人、每组8人、或每组12人,都正好分完,这个班学生接近50人,你知道五年级三班有多少学生吗?
应用题
50以内6的倍数有:6,12,18,24,30,36,42,48
50以内8的倍数有:8,16,24,32,40,48
50以内12的倍数有:12,24,36,48
答五年级三班有48人。
应用题
用 三张数字卡片按要求摆数
1)任意取两张数字卡片,可以摆出的2的倍数有( );可以摆出3的倍数有( );可以摆出的5的倍数有( )。
2
5
7
2)任意取;两张卡片摆出的数中,既有因数3又有因数5的数有( )。
3)摆出的所有三位数中,最大的是( ),最小的是( )。
52,72
72,27,57,75
25,75
75
752
257
通过本节课的复习,
你有什么收获?
