2.2 直线的方程 课件(共62张PPT)-2024-2025学年高二上学期数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 2.2 直线的方程 课件(共62张PPT)-2024-2025学年高二上学期数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-04 14:50:12 | ||
图片预览




文档简介
(共62张PPT)
第二章 直线与圆的方程
2.2 直线的方程
2.2.1 点斜式方程
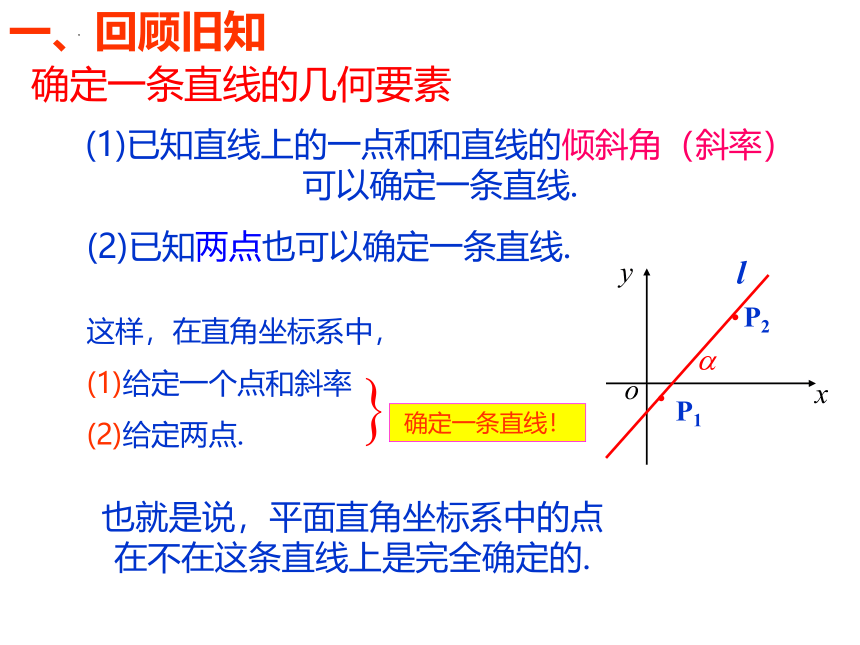
(1)已知直线上的一点和和直线的倾斜角(斜率)可以确定一条直线.
(2)已知两点也可以确定一条直线.
这样,在直角坐标系中,
(1)给定一个点和斜率
(2)给定两点.
确定一条直线的几何要素
确定一条直线!
也就是说,平面直角坐标系中的点 在不在这条直线上是完全确定的.
l
一、回顾旧知
P1
·
P2
·
y
x
O
P
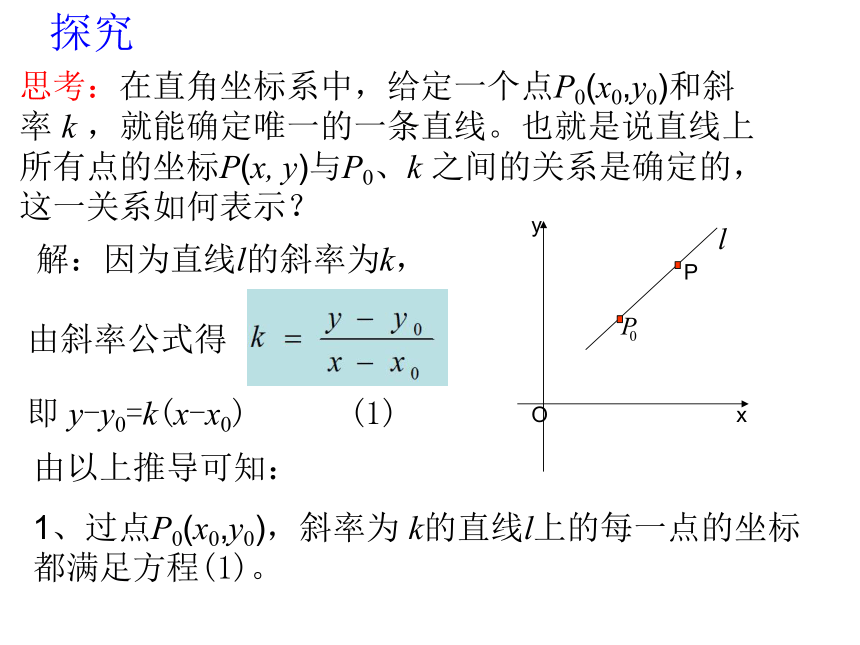
解:因为直线l的斜率为k,
由斜率公式得
即 y-y0=k(x-x0) (1)
探究
思考:在直角坐标系中,给定一个点P0(x0,y0)和斜率 k ,就能确定唯一的一条直线。也就是说直线上所有点的坐标P(x, y)与P0、k 之间的关系是确定的,这一关系如何表示?
由以上推导可知:
1、过点P0(x0,y0),斜率为 k的直线l上的每一点的坐标都满足方程(1)。
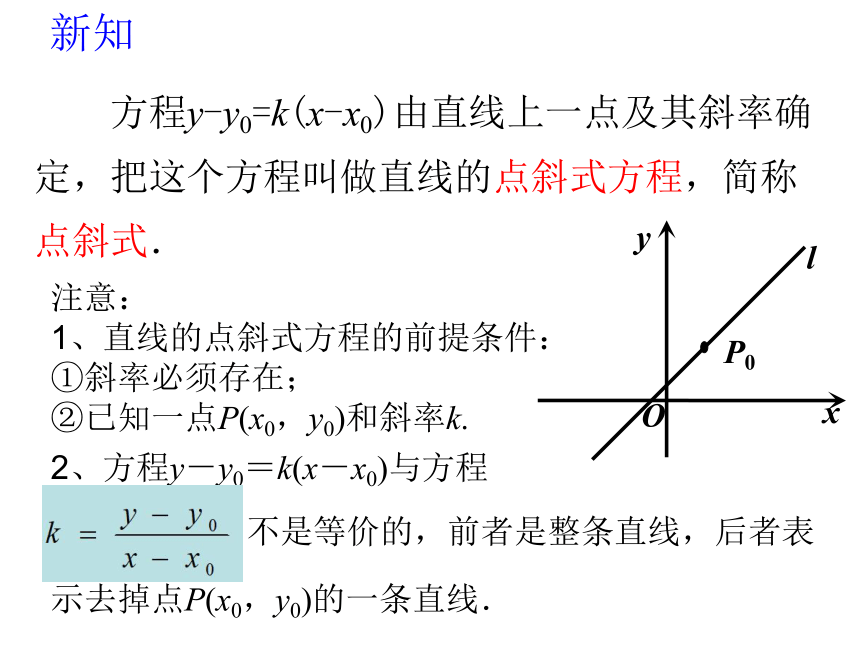
方程y-y0=k(x-x0)由直线上一点及其斜率确定,把这个方程叫做直线的点斜式方程,简称点斜式.
x
y
O
l
P0
新知
注意:
1、直线的点斜式方程的前提条件:①斜率必须存在;
②已知一点P(x0,y0)和斜率k.
2、方程y-y0=k(x-x0)与方程
不是等价的,前者是整条直线,后者表示去掉点P(x0,y0)的一条直线.
x
y
l
P0(x0,y0)
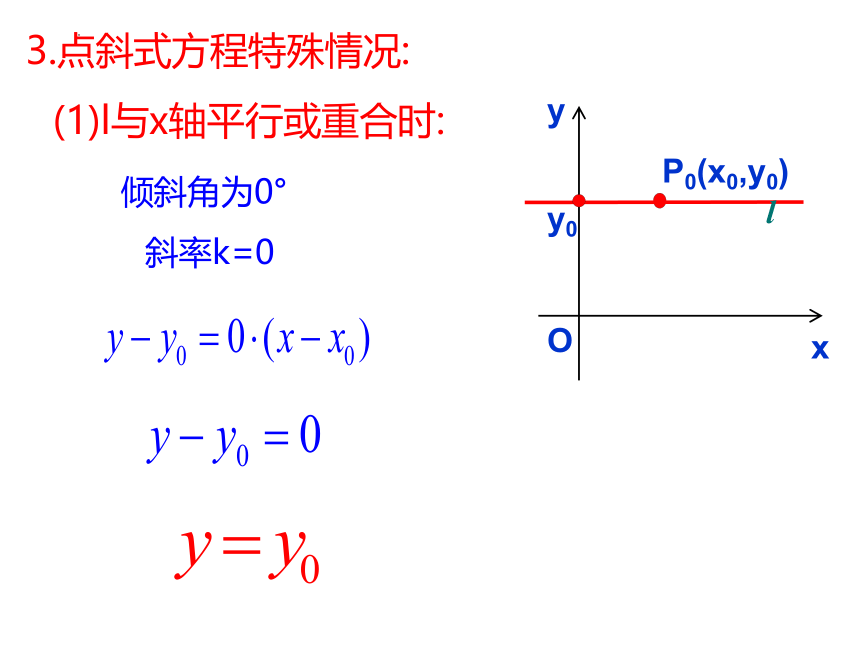
(1)l与x轴平行或重合时:
y0
O
倾斜角为0°
斜率k=0
3.点斜式方程特殊情况:
x
y
l
P0(x0,y0)
(2)l与x轴垂直时:
x0
O
倾斜角为90°
斜率k 不存在!
不能用点斜式求方程!
但是直线是存在的.
4.小结:点斜式方程
x
y
l
x
y
l
x
y
l
O
①倾斜角α≠90°
②倾斜角α=0°
③倾斜角α=90°
y0
x0
自学检测1:(10分钟)
1.写出下列直线的点斜式方程:
(1)斜率为3,经过点(5,-4);
(2)斜率为-2,经过点(0,2);
(3)经过点(-1,-1)且与x轴平行;
(4)经过点(1,1)且与x轴垂直.
2.(1)经过点(-5,2)且平行于y轴的直线方程为________.
(2)直线y=x+1绕着其上一点P(3,4)逆时针旋转90°后得直线l,则直线l的点斜式方程为________.
(3)求过点P(1,2)且与直线y=2x+1平行的直线方程为________.
x=-5
y-4=-(x-3)
y-2=2(x-1)
y+4=3(x-5)
y-2=-2x
y=-1
x=1
3.已知直线的点斜式方程是 y-2=x-1,那么此直线的斜率是_____,倾斜角是_____.
4.已知直线的点斜式方程是 y+2= (x+1),那么此直线的斜率是______,倾斜角是_____.
变式:已知直线kx-y+1-2k=0,当k变化时, 所有直线恒过定点________.
(2,1)
5.直线y+1=mx-3m(m∈R)必过定点 .
(3,-1)
6.求过点(1,2)且与两坐标轴组成一等腰直角三角形的直线方程.
2.直线的斜截式方程
x
y
P0(0,b)
已知直线l经过点P0(0,b),其斜率为k,求直线l的方程.
l
斜率
y轴上的截距
直线的斜截式方程,简称斜截式
①y轴上的截距:
(纵截距)
直线与y轴交点的纵坐标b.
②x轴上的截距:
(横截距)
直线与x轴交点的橫坐标a.
思考1:直线y=x的横截距和纵截距分别是多少
注意:截距是一个坐标,不是距离.截距可正、可负、可为零、可以不存在.
思考2:一次函数的解析式y=kx+b与直线的斜截式方程y=kx+b有什么区别
y-2=3(x-1)
自学检测2:(5分钟)
1.写出下列直线的斜截式方程:
(3)倾斜角为150°,在y轴上的截距是-2;
(1)斜率为2,在y轴上的截距是5;
(2)斜率为-2,与y轴的交点坐标为(0,-4);
(5)经过点A(-1,2),且与直线y=3x+1垂直.
(4)经过点(3,4)且在两坐标轴上的截距相等.
l1
x
y
b1
l2
b2
l1
x
y
l2
l1
1.当a为何值时,
(1)两直线y=ax-2与y=(a+2)x+1互相垂直
(2)两直线y=-x+4a与y=(a2-2)x+4互相平行
自学检测3:(6分钟)
两直线平行与垂直的应用
1.点斜式方程
当知道斜率和一点坐标时用点斜式
2.斜截式方程
当知道斜率k和截距b时用斜截式
3.特殊情况
①直线和x轴平行时,倾斜角α=0°
②直线与x轴垂直时,倾斜角α=90°
斜率存在!
四、课堂小结
方程名称 已知条件 直线方程 应用范围
点斜式
斜截式
K存在
K存在
复习:(1分钟)
1.已知直线l过A(3,-5)和B(-2,5),则直线l的方程为 .
y-(-5)=-2(x-3)
经过两个定点的直线的方程能否用“公式”直接写出来呢
两点确定一条直线!
第二章 直线与圆的方程
2.2 直线的方程
2.2.2 两点式方程
化成比例式:
思考1:设直线l经过两点P1(x1,y1),P2(x2,y2),(其中x1≠x2,y1≠y2),你能写出直线l的点斜式方程吗
思考:两点式的适用范围是 .
直线与两坐标轴不垂直
直线的两点式方程
经过直线上两点P1(x1,y1),P2(x2,y2)(其中x1≠x2,y1≠y2)的直线方程叫做直线的两点式方程,简称两点式.
当x1=x2时,直线l的方程是 ;
当y1=y2时,直线l的方程是 .
x=x1
y=y1
与x轴垂直
与y轴垂直
练习1.求经过下列两点的直线方程:
x
y
O
B
.
A
.
.
C
解:过B(3,-3),C(0,2)两点式方程为:
这就是BC边所在直线的方程.
.
M
练:1. 三角形的顶点是A(-5,0),B(3,-3),C(0,2), 求BC边所在直线的方程,以及该边上中线所在直线的方程.
中点坐标公式
x
y
O
B
.
A
.
.
C
.
M
变式:已知△ABC三个顶点的坐标分别为A(1,3),B(-2,-3),C(4,0). (1)求AB所在直线的方程; (2)求BC边上的高所在的直线方程.
x
l
B(0,b)
A(a,0)
O
y
将A(a,0),B(0,b)代入两点式得:
思考2:已知直线l与x轴的交点为A(a,0),与y轴的交点为B(0,b)其中a≠0,b≠0,求直线l的方程.
直线的截距式方程
在y轴上的截距
在x轴上的截距
横、纵截距都存在且都不为0的直线.
直线方程由直线在x轴和y轴的截距确定,所以叫做直线方程的截距式方程.
思考:截距式的适用范围是 .
①不与坐标轴垂直;
②不过原点;
练习1.求下列直线的方程:
(1)在x轴上的截距是2,在y轴上的截距是3;
(2)在x轴上的截距是-5,在y轴上的截距是6;
3.根据下列条件,求直线的方程: (1)过点(0,5),且在两坐标轴上的截距之和为2;
(2)过点(5,0),且在两坐标轴上的截距之差为2.
4.直线 经过一、二、四象限,
则a 0,b 0.
5.求经过点P(-5,4),且在两坐标轴上的截距相等的直线方程.
o
x
y
②截距不为0,设截距式求解.
注意分类讨论!
①截距均为0时,设方程为y=kx,
解:(1)当截距均为0时,设方程为y=kx,
把P(-5,4)代入上式得
即直线方程为
(2)当截距均不为0时,设直线方程为
把P(-5,4)代入上式得
直线方程为
即
综上直线方程为 或
求经过点A(-3,4),且在两坐标轴上截距互为相反数的直线l的方程.
思考1:直线方程有几种形式 指明它们的条件及应用范围.
1.点斜式
y-y0=k(x-x0)
2.斜截式
y=kx+b
3.两点式
4.截距式
知识探究:
适用范围
斜率存在
斜率存在
直线不与坐标轴垂直
②直线不过原点
①直线不与坐标轴垂直
1.问题情境一
数学家笛卡儿在平面直角坐标系中研究两直线间的位置关系时,碰到了这样一个问题:平面直角坐标系中的任何一条直线l能不能用一种自然优美的“万能”形式的方程来表示
思考2:上述四种直线方程,能否写成如下统一形式
x+ y+ =0
上述四式都可以写成直线方程的一般形式:
Ax+By+C=0,A、B不同时为0.
2.问题情境二
数学家笛卡儿接着思考:
每一个关于x , y的二元一次方程都表示直线吗
①当B≠0时
②当B=0时
l
x
y
O
方程可化为
这是直线的斜截式方程,它表示斜率是
在y轴上的截距是 的直线。
表示垂直于x轴的一条直线
方程可化为
思考::所有的直线都可以用二元一次方程表示?
定义:我们把关于x,y的二元一次方程
叫做直线的一般式方程,简称一般式.
直线方程的一般式
Ax+By+C=0(其中A,B不同时为0)
一般式可以表示任何类型的直线而不受条件限制.
自学检测1:(12分钟)
4x+3y-12=0
2.已知直线经过点A(2,-1),斜率为-3,求直线的点斜式和一般式方程.
对于直线方程的一般式,一般作如下约定: x的系数为正,x,y的系数及常数项一般不出现分数,一般按含x项、含y项、常数项顺序排列、
3.把直线l的方程x–2y+6=0化成斜截式,求出
直线l的斜率和它在x轴与y轴上的截距,并画图.
x
y
O
B
A
.
.
C
2.若直线l的一般式方程为2x-y+1=0,则直线l不经过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
3.在方程Ax+By+C=0中,A,B,C为何值时,方程表示的直线: (1)平行于x轴; (2)平行于y轴; (3)与x轴重合; (4)与y轴重合; (5)过原点; (6)与x轴和y轴相交;
x
y
0
(1)A=0,B≠0,C≠0;
x
y
0
(2)B=0,A≠0,C≠0;
(3)A=0,B≠0,C=0;
x
y
0
3.在方程Ax+By+C=0中,A,B,C为何值时,方程表示的直线: (3)与x轴重合; (4)与y轴重合;
x
y
0
(4)B=0,A≠0,C=0;
(5)C=0,A、B不同时为0;
x
y
0
3.在方程Ax+By+C=0中,A,B,C为何值时,方程表示的直线: (5)过原点; (6)与x轴和y轴相交;
(6)A≠0,B≠0;
x
y
0
4.已知直线Ax+By+C=0的斜率为5, 且A-2B+3C=0,求直线的方程.
方法:只要给出两个条件,就可以求出直线方程.
知识点2:定点问题
直线y-y0=k(x-x0)恒过定点_________.
直线y=k(x-x0)恒过定点_________.
直线y=kx恒过定点_________.
恒过定点:
(0, 0)
(x0, 0)
(x0, y0)
无论参数k取什么值,直线都经过过定点。
直线y=k(x-2)恒过定点_________.
(2, 0)
知识点3:定点问题
分离参数法
数形结合
知识点4:对称问题
点关于点对称:
A
(x0,y0)
P
(x1,y1)
Q
(x2,y2)
点关于直线对称:
M
P
(x0,y0)
P’
(x,y)
Ax+By+C=0
C
小结:
点斜式
斜率和一点坐标
斜截式
斜率k和截距b
两点坐标
两点式
点斜式
两个截距
截距式
化成一般式
Ax+By+C=0
第二章 直线与圆的方程
2.2 直线的方程
2.2.1 点斜式方程
(1)已知直线上的一点和和直线的倾斜角(斜率)可以确定一条直线.
(2)已知两点也可以确定一条直线.
这样,在直角坐标系中,
(1)给定一个点和斜率
(2)给定两点.
确定一条直线的几何要素
确定一条直线!
也就是说,平面直角坐标系中的点 在不在这条直线上是完全确定的.
l
一、回顾旧知
P1
·
P2
·
y
x
O
P
解:因为直线l的斜率为k,
由斜率公式得
即 y-y0=k(x-x0) (1)
探究
思考:在直角坐标系中,给定一个点P0(x0,y0)和斜率 k ,就能确定唯一的一条直线。也就是说直线上所有点的坐标P(x, y)与P0、k 之间的关系是确定的,这一关系如何表示?
由以上推导可知:
1、过点P0(x0,y0),斜率为 k的直线l上的每一点的坐标都满足方程(1)。
方程y-y0=k(x-x0)由直线上一点及其斜率确定,把这个方程叫做直线的点斜式方程,简称点斜式.
x
y
O
l
P0
新知
注意:
1、直线的点斜式方程的前提条件:①斜率必须存在;
②已知一点P(x0,y0)和斜率k.
2、方程y-y0=k(x-x0)与方程
不是等价的,前者是整条直线,后者表示去掉点P(x0,y0)的一条直线.
x
y
l
P0(x0,y0)
(1)l与x轴平行或重合时:
y0
O
倾斜角为0°
斜率k=0
3.点斜式方程特殊情况:
x
y
l
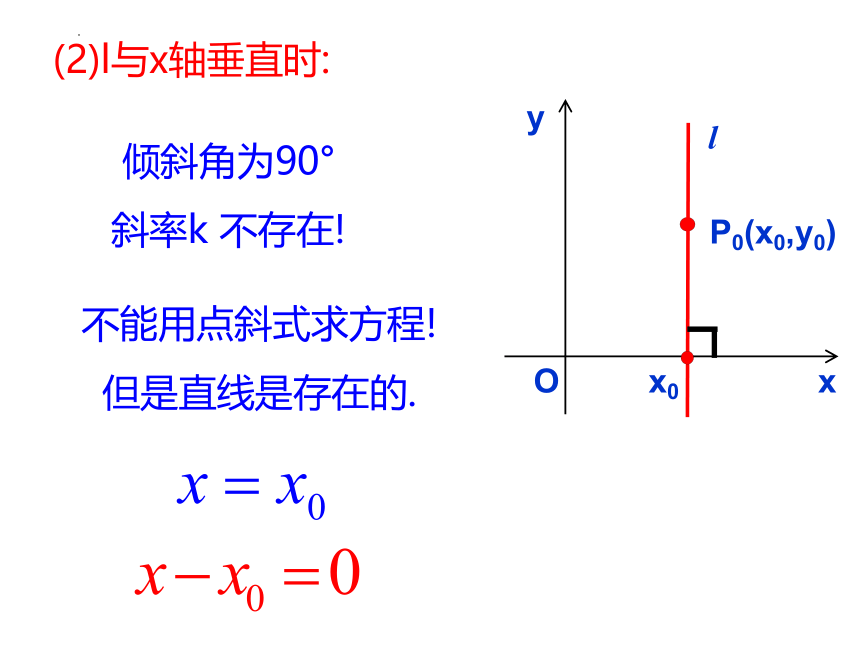
P0(x0,y0)
(2)l与x轴垂直时:
x0
O
倾斜角为90°
斜率k 不存在!
不能用点斜式求方程!
但是直线是存在的.
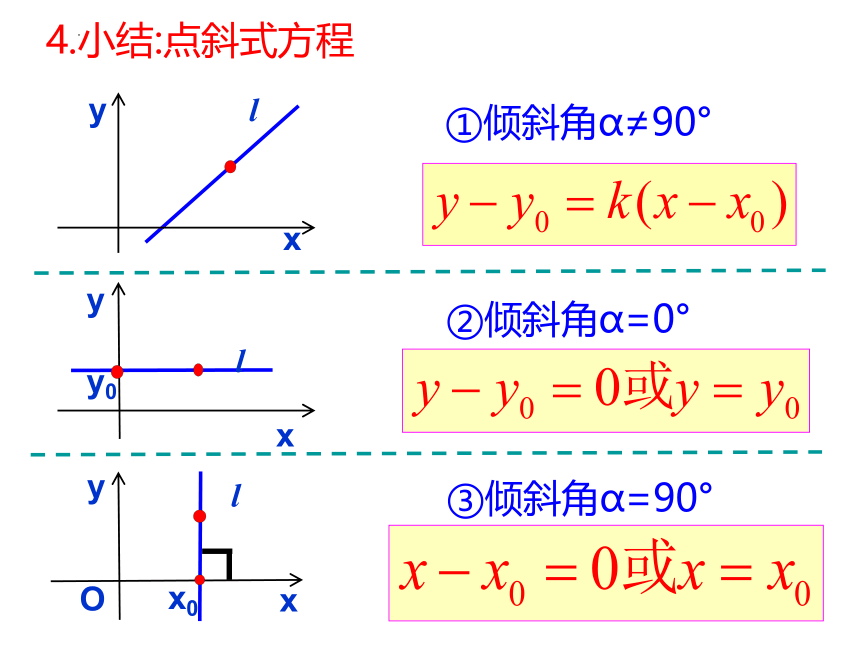
4.小结:点斜式方程
x
y
l
x
y
l
x
y
l
O
①倾斜角α≠90°
②倾斜角α=0°
③倾斜角α=90°
y0
x0
自学检测1:(10分钟)
1.写出下列直线的点斜式方程:
(1)斜率为3,经过点(5,-4);
(2)斜率为-2,经过点(0,2);
(3)经过点(-1,-1)且与x轴平行;
(4)经过点(1,1)且与x轴垂直.
2.(1)经过点(-5,2)且平行于y轴的直线方程为________.
(2)直线y=x+1绕着其上一点P(3,4)逆时针旋转90°后得直线l,则直线l的点斜式方程为________.
(3)求过点P(1,2)且与直线y=2x+1平行的直线方程为________.
x=-5
y-4=-(x-3)
y-2=2(x-1)
y+4=3(x-5)
y-2=-2x
y=-1
x=1
3.已知直线的点斜式方程是 y-2=x-1,那么此直线的斜率是_____,倾斜角是_____.
4.已知直线的点斜式方程是 y+2= (x+1),那么此直线的斜率是______,倾斜角是_____.
变式:已知直线kx-y+1-2k=0,当k变化时, 所有直线恒过定点________.
(2,1)
5.直线y+1=mx-3m(m∈R)必过定点 .
(3,-1)
6.求过点(1,2)且与两坐标轴组成一等腰直角三角形的直线方程.
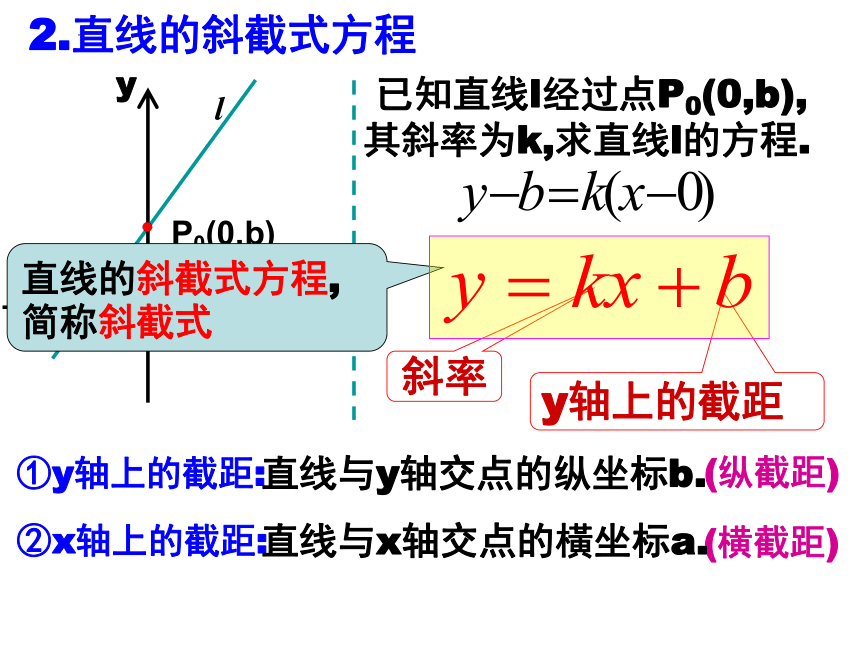
2.直线的斜截式方程
x
y
P0(0,b)
已知直线l经过点P0(0,b),其斜率为k,求直线l的方程.
l
斜率
y轴上的截距
直线的斜截式方程,简称斜截式
①y轴上的截距:
(纵截距)
直线与y轴交点的纵坐标b.
②x轴上的截距:
(横截距)
直线与x轴交点的橫坐标a.
思考1:直线y=x的横截距和纵截距分别是多少
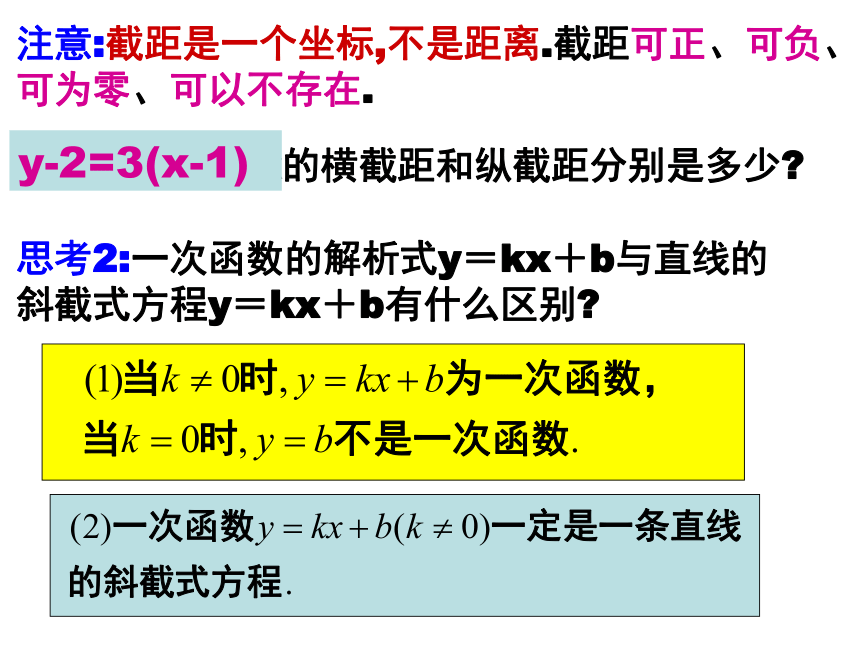
注意:截距是一个坐标,不是距离.截距可正、可负、可为零、可以不存在.
思考2:一次函数的解析式y=kx+b与直线的斜截式方程y=kx+b有什么区别
y-2=3(x-1)
自学检测2:(5分钟)
1.写出下列直线的斜截式方程:
(3)倾斜角为150°,在y轴上的截距是-2;
(1)斜率为2,在y轴上的截距是5;
(2)斜率为-2,与y轴的交点坐标为(0,-4);
(5)经过点A(-1,2),且与直线y=3x+1垂直.
(4)经过点(3,4)且在两坐标轴上的截距相等.
l1
x
y
b1
l2
b2
l1
x
y
l2
l1
1.当a为何值时,
(1)两直线y=ax-2与y=(a+2)x+1互相垂直
(2)两直线y=-x+4a与y=(a2-2)x+4互相平行
自学检测3:(6分钟)
两直线平行与垂直的应用
1.点斜式方程
当知道斜率和一点坐标时用点斜式
2.斜截式方程
当知道斜率k和截距b时用斜截式
3.特殊情况
①直线和x轴平行时,倾斜角α=0°
②直线与x轴垂直时,倾斜角α=90°
斜率存在!
四、课堂小结
方程名称 已知条件 直线方程 应用范围
点斜式
斜截式
K存在
K存在
复习:(1分钟)
1.已知直线l过A(3,-5)和B(-2,5),则直线l的方程为 .
y-(-5)=-2(x-3)
经过两个定点的直线的方程能否用“公式”直接写出来呢
两点确定一条直线!
第二章 直线与圆的方程
2.2 直线的方程
2.2.2 两点式方程
化成比例式:
思考1:设直线l经过两点P1(x1,y1),P2(x2,y2),(其中x1≠x2,y1≠y2),你能写出直线l的点斜式方程吗
思考:两点式的适用范围是 .
直线与两坐标轴不垂直
直线的两点式方程
经过直线上两点P1(x1,y1),P2(x2,y2)(其中x1≠x2,y1≠y2)的直线方程叫做直线的两点式方程,简称两点式.
当x1=x2时,直线l的方程是 ;
当y1=y2时,直线l的方程是 .
x=x1
y=y1
与x轴垂直
与y轴垂直
练习1.求经过下列两点的直线方程:
x
y
O
B
.
A
.
.
C
解:过B(3,-3),C(0,2)两点式方程为:
这就是BC边所在直线的方程.
.
M
练:1. 三角形的顶点是A(-5,0),B(3,-3),C(0,2), 求BC边所在直线的方程,以及该边上中线所在直线的方程.
中点坐标公式
x
y
O
B
.
A
.
.
C
.
M
变式:已知△ABC三个顶点的坐标分别为A(1,3),B(-2,-3),C(4,0). (1)求AB所在直线的方程; (2)求BC边上的高所在的直线方程.
x
l
B(0,b)
A(a,0)
O
y
将A(a,0),B(0,b)代入两点式得:
思考2:已知直线l与x轴的交点为A(a,0),与y轴的交点为B(0,b)其中a≠0,b≠0,求直线l的方程.
直线的截距式方程
在y轴上的截距
在x轴上的截距
横、纵截距都存在且都不为0的直线.
直线方程由直线在x轴和y轴的截距确定,所以叫做直线方程的截距式方程.
思考:截距式的适用范围是 .
①不与坐标轴垂直;
②不过原点;
练习1.求下列直线的方程:
(1)在x轴上的截距是2,在y轴上的截距是3;
(2)在x轴上的截距是-5,在y轴上的截距是6;
3.根据下列条件,求直线的方程: (1)过点(0,5),且在两坐标轴上的截距之和为2;
(2)过点(5,0),且在两坐标轴上的截距之差为2.
4.直线 经过一、二、四象限,
则a 0,b 0.
5.求经过点P(-5,4),且在两坐标轴上的截距相等的直线方程.
o
x
y
②截距不为0,设截距式求解.
注意分类讨论!
①截距均为0时,设方程为y=kx,
解:(1)当截距均为0时,设方程为y=kx,
把P(-5,4)代入上式得
即直线方程为
(2)当截距均不为0时,设直线方程为
把P(-5,4)代入上式得
直线方程为
即
综上直线方程为 或
求经过点A(-3,4),且在两坐标轴上截距互为相反数的直线l的方程.
思考1:直线方程有几种形式 指明它们的条件及应用范围.
1.点斜式
y-y0=k(x-x0)
2.斜截式
y=kx+b
3.两点式
4.截距式
知识探究:
适用范围
斜率存在
斜率存在
直线不与坐标轴垂直
②直线不过原点
①直线不与坐标轴垂直
1.问题情境一
数学家笛卡儿在平面直角坐标系中研究两直线间的位置关系时,碰到了这样一个问题:平面直角坐标系中的任何一条直线l能不能用一种自然优美的“万能”形式的方程来表示
思考2:上述四种直线方程,能否写成如下统一形式
x+ y+ =0
上述四式都可以写成直线方程的一般形式:
Ax+By+C=0,A、B不同时为0.
2.问题情境二
数学家笛卡儿接着思考:
每一个关于x , y的二元一次方程都表示直线吗
①当B≠0时
②当B=0时
l
x
y
O
方程可化为
这是直线的斜截式方程,它表示斜率是
在y轴上的截距是 的直线。
表示垂直于x轴的一条直线
方程可化为
思考::所有的直线都可以用二元一次方程表示?
定义:我们把关于x,y的二元一次方程
叫做直线的一般式方程,简称一般式.
直线方程的一般式
Ax+By+C=0(其中A,B不同时为0)
一般式可以表示任何类型的直线而不受条件限制.
自学检测1:(12分钟)
4x+3y-12=0
2.已知直线经过点A(2,-1),斜率为-3,求直线的点斜式和一般式方程.
对于直线方程的一般式,一般作如下约定: x的系数为正,x,y的系数及常数项一般不出现分数,一般按含x项、含y项、常数项顺序排列、
3.把直线l的方程x–2y+6=0化成斜截式,求出
直线l的斜率和它在x轴与y轴上的截距,并画图.
x
y
O
B
A
.
.
C
2.若直线l的一般式方程为2x-y+1=0,则直线l不经过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
3.在方程Ax+By+C=0中,A,B,C为何值时,方程表示的直线: (1)平行于x轴; (2)平行于y轴; (3)与x轴重合; (4)与y轴重合; (5)过原点; (6)与x轴和y轴相交;
x
y
0
(1)A=0,B≠0,C≠0;
x
y
0
(2)B=0,A≠0,C≠0;
(3)A=0,B≠0,C=0;
x
y
0
3.在方程Ax+By+C=0中,A,B,C为何值时,方程表示的直线: (3)与x轴重合; (4)与y轴重合;
x
y
0
(4)B=0,A≠0,C=0;
(5)C=0,A、B不同时为0;
x
y
0
3.在方程Ax+By+C=0中,A,B,C为何值时,方程表示的直线: (5)过原点; (6)与x轴和y轴相交;
(6)A≠0,B≠0;
x
y
0
4.已知直线Ax+By+C=0的斜率为5, 且A-2B+3C=0,求直线的方程.
方法:只要给出两个条件,就可以求出直线方程.
知识点2:定点问题
直线y-y0=k(x-x0)恒过定点_________.
直线y=k(x-x0)恒过定点_________.
直线y=kx恒过定点_________.
恒过定点:
(0, 0)
(x0, 0)
(x0, y0)
无论参数k取什么值,直线都经过过定点。
直线y=k(x-2)恒过定点_________.
(2, 0)
知识点3:定点问题
分离参数法
数形结合
知识点4:对称问题
点关于点对称:
A
(x0,y0)
P
(x1,y1)
Q
(x2,y2)
点关于直线对称:
M
P
(x0,y0)
P’
(x,y)
Ax+By+C=0
C
小结:
点斜式
斜率和一点坐标
斜截式
斜率k和截距b
两点坐标
两点式
点斜式
两个截距
截距式
化成一般式
Ax+By+C=0
