24.1 圆的有关性质同步练习2024—2025学年人教版数学九年级上册(含答案)
文档属性
| 名称 | 24.1 圆的有关性质同步练习2024—2025学年人教版数学九年级上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 663.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-04 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
24.1 圆的有关性质
24.1.1 圆
要点归纳
知识要点 圆的有关概念
1.圆的基本概念:①在一个平面内,线段 OA 绕它固定的一个端点O 旋转一周,另一个端点A 所形成的图形叫做圆,记作⊙O.②圆是所有到圆心的距离等于 的点的集合.
2.和圆有关的概念:①连接圆上任意两点的线段叫做 ,经过圆心的弦叫做 .②圆上任意两点间的部分叫做圆弧,简称弧;圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆;大于半圆的弧叫做 ,小于半圆的弧叫做 .
当堂检测 (建议用时:10分钟)
1.下列说法中,不正确的是 ( )
A.直径是弦,弦是直径
B.半圆周是弧
C.圆上的点到圆心的距离都相等
D.同圆或等圆中,优弧一定比劣弧长
2.下列图形中,四个顶点一定在同一个圆上的是 ( )
A.平行四边形 B.矩形
C.菱形 D.任意四边形
3.有一个圆的半径为5,则该圆的弦长不可能是 ( )
A.1 B.4
C.10 D.11
4.如图,在⊙O中,AB 是直径,AC 是弦,连接OC,若∠ACO=25°,则∠BOC 的度数是( )
A.40° B.50°
C.55° D.60°
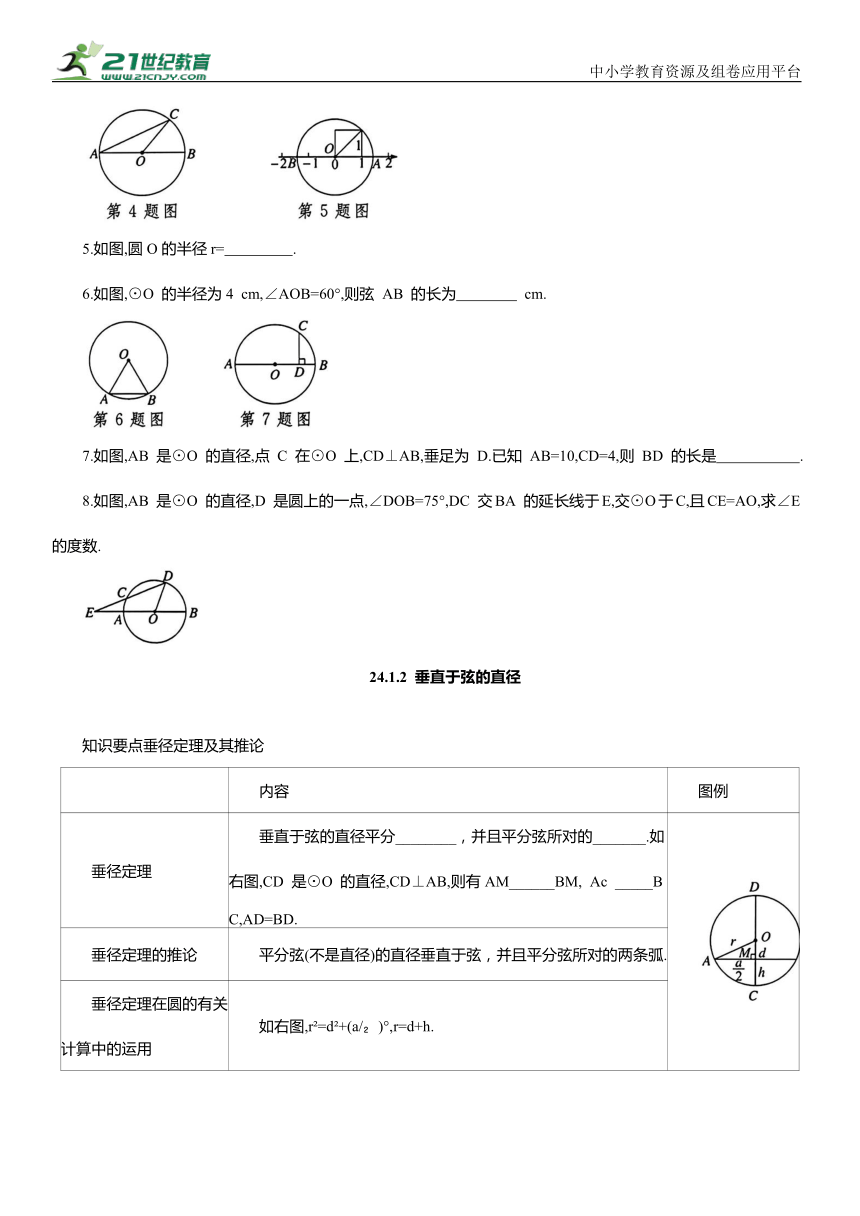
5.如图,圆O的半径r= .
6.如图,⊙O 的半径为4 cm,∠AOB=60°,则弦 AB 的长为 cm.
7.如图,AB 是⊙O 的直径,点 C 在⊙O 上,CD⊥AB,垂足为 D.已知 AB=10,CD=4,则 BD 的长是 .
8.如图,AB 是⊙O 的直径,D 是圆上的一点,∠DOB=75°,DC 交BA 的延长线于E,交⊙O于C,且CE=AO,求∠E 的度数.
24.1.2 垂直于弦的直径
知识要点垂径定理及其推论
内容 图例
垂径定理 垂直于弦的直径平分________,并且平分弦所对的_______.如右图,CD 是⊙O 的直径,CD⊥AB,则有AM______BM, Ac _____BC,AD=BD.
垂径定理的推论 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
垂径定理在圆的有关计算中的运用 如右图,r =d +(a/ )°,r=d+h.
易错提醒 圆中两条平行的弦的位置分两弦在圆心同侧和异侧两种情况.注意画图并分情况讨论.
当堂检测 (建议用时:15 分钟)
1.如图,AB 是⊙O 的直径,AB⊥CD 于 E点,若CD=6,则 DE 的长为 ( )
A.3 B.4 C.5 D.6
2.如图,已知⊙O 的半径为13,弦 AB 长为24,则点 O 到AB 的距离是 ( )
A.6 B.5 C.4 D.3
3.如图,在⊙O中,半径OD 垂直于弦AB,垂足为C,OD=13cm,AB═24 cm,则CD═ cm.
4.如图,AE 是⊙O 的直径,半径 OD 垂直于弦AB,垂足为C,AB=8cm,CD=2cm,则BE 的长是 cm.
5.一根横截面为圆形的下水管道的直径为1米,管内有少量的污水(如图),此时的水面宽 AB 为 0.6米.
(1)求此时的水深(即阴影部分弓形的高);
(2)当水位上升到水面宽为0.8 米时,求水面上升的高度.
24.1.3 弧、弦、圆心角
要点归纳
知识要点 弧、弦、圆心角
内容 图例
弧、弦、圆心角之间的关系定理 在同圆或等圆中,相等的圆心角所对的_________相等,所对的________也相等. 如果∠AOB=∠COD,那么 AB=CD,AB=CD; 如果AB=CD,那么∠AOB= ∠COD,AB=CD; 如果 AB=CD,那么∠AOB=∠COD,AB=CD.
弧、弦、圆心角之间的关系定理的推广 同圆或等圆中,两个圆心角、两条弧、两条弦中如果有一组量相等,那么它们所对应的其余各组量也相等(注意:一条弦对应两条弧).
当堂检测 (建议用时:10分钟)
1.下列四个命题:①同圆或等圆中,相等的弧所对的圆心角相等;②同圆或等圆中,相等的圆心角所对的弧相等;③同圆或等圆中,相等的弦所对的弧相等;④同圆或等圆中,相等的弧所对的弦相等.真命题的个数有( )
A.1 个 B.2 个 C.3 个 C.4 个
2.如图,在⊙O中, 若∠AOB=40°,则∠COD= °.
3.如图,AB 是⊙O 的弦,C 是. 的中点,OC交AB 于点 D.
(1)若∠AOB=120°,则∠AOC= °;
(2)若AB=8cm,则AD= cm.
4.如图,在⊙O 中, 若.∠B=65°,则∠A 的度数是 .
5.如图,AB 是⊙O 的直径,点 C,D 在⊙O上.若 则∠COD =
°.
6.如图,C 为. 的中点,CN⊥OB 于N,弦CD⊥OA 于 M,CN = 4 cm,则 CD = cm.
7.如图,AD=CB,求证:AB=CD.
24.1.4圆周角
知识要点 圆周角定理及其推论
圆周角 内容 图例
概念 顶点在______,并且两边都与圆_______,我们把这样的角叫做圆周角. 如图①,∠BAC=∠BDC ∠BOC如图②,若 BC 为⊙O 的直径,则∠BAC =_________;若∠BAC =90°,则 BC 为⊙O 的________.如图②,∠1+∠2=_______.
圆周角定理 一条弧所对的圆周角等于它所对的圆心角的_______.
圆周角定理的推论 1.同弧或等弧所对的圆周角_______. 2.半圆(或直径)所对的圆周角是________,90°的圆周角所对的弦是_______. 3.圆内接四边形的对角________.
解题策略 ①在圆中,利用“直径所对的圆周角是直角”构造直角三角形解题. ②一条弦所对的圆周角有两种情况:相等或互补.
当堂检测 (建议用时:10 分钟)
1.如图,已知圆心角∠BOC=78°,则圆周角∠BAC 的度数是 ( )
A.156° B.78° C.39° D.12°
2.如图,已 知 四 边 形 ABCD 内接于 ⊙O,∠ABC=60°,则∠CDE 的度数是 .
3.如图,四边形ABCD 是⊙O 的内接四边形,若∠C=110°,则∠BOD= °.
4.如图,AB 是⊙O 的直径,若AC=4,∠D=60°,则∠A= °,AB= .
5.如图,在△ABC 中,AB=AC,AB 是⊙O的直径,⊙O 交底边 BC 于点 D,交 AC 于点E,连接 DE.求证:BD=DE=DC.
24.1 圆的有关性质
24.1.1 圆
要点归纳
知识要点:半径 弦 直径 优弧 劣弧当堂检测
1. A 2. B 3. D 4. B 5. 6.4 7.2
8.解:如图,连接OC.∵CE=AO,而OA=OC,∴OC=EC,∴∠E=∠1,∴∠2=∠E+∠1=2∠E.∵OC=OD,∴∠CDO=∠2=2∠E.∵∠BOD = ∠E +∠CDO,∴∠E+2∠E=75°,∴∠E=25°.
24.1.2 垂直于弦的直径要点归纳
知识要点:弦 两条弧 = =
当堂检测
1. A 2. B 3.8 4.6
5.解:(1)如图,作半径OD⊥AB于C,连接 OB.由垂径定理得 在 Rt△OBC中, 0.4=0.1,此时的水深为0.1米.
(2)当水位上升到圆心以下时,水面宽为0.8米,则 水面上升的高度为0.4—0.3=0.1(米);当水位上升到圆心以上时,水面上升的高度为0.4+0.3=0.7(米).综上可得,水面上升的高度为0.1米或0.7 米.
24.1.3 弧、弦、圆心角
要点归纳
知识要点:弧 弦
当堂检测
1. C 2.40 3.(1)60 (2)4
4.50° 5.140 6.8
7.证明: 即(CD=AB,∴AB=CD.
24.1.4 圆周角
要点归纳
知识要点:圆上 相交 一半 相等 直角直径 互补 90° 直径 180°当堂检测
1. C 2.60° 3.140 4.60 8
5.证明:连接AD.∵AB 是直径,∴∠ADB=90°.∴AD⊥BC.∵AB=AC,∴BD=DC, DE.∴BD=DE=DC.
24.1 圆的有关性质
24.1.1 圆
要点归纳
知识要点 圆的有关概念
1.圆的基本概念:①在一个平面内,线段 OA 绕它固定的一个端点O 旋转一周,另一个端点A 所形成的图形叫做圆,记作⊙O.②圆是所有到圆心的距离等于 的点的集合.
2.和圆有关的概念:①连接圆上任意两点的线段叫做 ,经过圆心的弦叫做 .②圆上任意两点间的部分叫做圆弧,简称弧;圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆;大于半圆的弧叫做 ,小于半圆的弧叫做 .
当堂检测 (建议用时:10分钟)
1.下列说法中,不正确的是 ( )
A.直径是弦,弦是直径
B.半圆周是弧
C.圆上的点到圆心的距离都相等
D.同圆或等圆中,优弧一定比劣弧长
2.下列图形中,四个顶点一定在同一个圆上的是 ( )
A.平行四边形 B.矩形
C.菱形 D.任意四边形
3.有一个圆的半径为5,则该圆的弦长不可能是 ( )
A.1 B.4
C.10 D.11
4.如图,在⊙O中,AB 是直径,AC 是弦,连接OC,若∠ACO=25°,则∠BOC 的度数是( )
A.40° B.50°
C.55° D.60°
5.如图,圆O的半径r= .
6.如图,⊙O 的半径为4 cm,∠AOB=60°,则弦 AB 的长为 cm.
7.如图,AB 是⊙O 的直径,点 C 在⊙O 上,CD⊥AB,垂足为 D.已知 AB=10,CD=4,则 BD 的长是 .
8.如图,AB 是⊙O 的直径,D 是圆上的一点,∠DOB=75°,DC 交BA 的延长线于E,交⊙O于C,且CE=AO,求∠E 的度数.
24.1.2 垂直于弦的直径
知识要点垂径定理及其推论
内容 图例
垂径定理 垂直于弦的直径平分________,并且平分弦所对的_______.如右图,CD 是⊙O 的直径,CD⊥AB,则有AM______BM, Ac _____BC,AD=BD.
垂径定理的推论 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
垂径定理在圆的有关计算中的运用 如右图,r =d +(a/ )°,r=d+h.
易错提醒 圆中两条平行的弦的位置分两弦在圆心同侧和异侧两种情况.注意画图并分情况讨论.
当堂检测 (建议用时:15 分钟)
1.如图,AB 是⊙O 的直径,AB⊥CD 于 E点,若CD=6,则 DE 的长为 ( )
A.3 B.4 C.5 D.6
2.如图,已知⊙O 的半径为13,弦 AB 长为24,则点 O 到AB 的距离是 ( )
A.6 B.5 C.4 D.3
3.如图,在⊙O中,半径OD 垂直于弦AB,垂足为C,OD=13cm,AB═24 cm,则CD═ cm.
4.如图,AE 是⊙O 的直径,半径 OD 垂直于弦AB,垂足为C,AB=8cm,CD=2cm,则BE 的长是 cm.
5.一根横截面为圆形的下水管道的直径为1米,管内有少量的污水(如图),此时的水面宽 AB 为 0.6米.
(1)求此时的水深(即阴影部分弓形的高);
(2)当水位上升到水面宽为0.8 米时,求水面上升的高度.
24.1.3 弧、弦、圆心角
要点归纳
知识要点 弧、弦、圆心角
内容 图例
弧、弦、圆心角之间的关系定理 在同圆或等圆中,相等的圆心角所对的_________相等,所对的________也相等. 如果∠AOB=∠COD,那么 AB=CD,AB=CD; 如果AB=CD,那么∠AOB= ∠COD,AB=CD; 如果 AB=CD,那么∠AOB=∠COD,AB=CD.
弧、弦、圆心角之间的关系定理的推广 同圆或等圆中,两个圆心角、两条弧、两条弦中如果有一组量相等,那么它们所对应的其余各组量也相等(注意:一条弦对应两条弧).
当堂检测 (建议用时:10分钟)
1.下列四个命题:①同圆或等圆中,相等的弧所对的圆心角相等;②同圆或等圆中,相等的圆心角所对的弧相等;③同圆或等圆中,相等的弦所对的弧相等;④同圆或等圆中,相等的弧所对的弦相等.真命题的个数有( )
A.1 个 B.2 个 C.3 个 C.4 个
2.如图,在⊙O中, 若∠AOB=40°,则∠COD= °.
3.如图,AB 是⊙O 的弦,C 是. 的中点,OC交AB 于点 D.
(1)若∠AOB=120°,则∠AOC= °;
(2)若AB=8cm,则AD= cm.
4.如图,在⊙O 中, 若.∠B=65°,则∠A 的度数是 .
5.如图,AB 是⊙O 的直径,点 C,D 在⊙O上.若 则∠COD =
°.
6.如图,C 为. 的中点,CN⊥OB 于N,弦CD⊥OA 于 M,CN = 4 cm,则 CD = cm.
7.如图,AD=CB,求证:AB=CD.
24.1.4圆周角
知识要点 圆周角定理及其推论
圆周角 内容 图例
概念 顶点在______,并且两边都与圆_______,我们把这样的角叫做圆周角. 如图①,∠BAC=∠BDC ∠BOC如图②,若 BC 为⊙O 的直径,则∠BAC =_________;若∠BAC =90°,则 BC 为⊙O 的________.如图②,∠1+∠2=_______.
圆周角定理 一条弧所对的圆周角等于它所对的圆心角的_______.
圆周角定理的推论 1.同弧或等弧所对的圆周角_______. 2.半圆(或直径)所对的圆周角是________,90°的圆周角所对的弦是_______. 3.圆内接四边形的对角________.
解题策略 ①在圆中,利用“直径所对的圆周角是直角”构造直角三角形解题. ②一条弦所对的圆周角有两种情况:相等或互补.
当堂检测 (建议用时:10 分钟)
1.如图,已知圆心角∠BOC=78°,则圆周角∠BAC 的度数是 ( )
A.156° B.78° C.39° D.12°
2.如图,已 知 四 边 形 ABCD 内接于 ⊙O,∠ABC=60°,则∠CDE 的度数是 .
3.如图,四边形ABCD 是⊙O 的内接四边形,若∠C=110°,则∠BOD= °.
4.如图,AB 是⊙O 的直径,若AC=4,∠D=60°,则∠A= °,AB= .
5.如图,在△ABC 中,AB=AC,AB 是⊙O的直径,⊙O 交底边 BC 于点 D,交 AC 于点E,连接 DE.求证:BD=DE=DC.
24.1 圆的有关性质
24.1.1 圆
要点归纳
知识要点:半径 弦 直径 优弧 劣弧当堂检测
1. A 2. B 3. D 4. B 5. 6.4 7.2
8.解:如图,连接OC.∵CE=AO,而OA=OC,∴OC=EC,∴∠E=∠1,∴∠2=∠E+∠1=2∠E.∵OC=OD,∴∠CDO=∠2=2∠E.∵∠BOD = ∠E +∠CDO,∴∠E+2∠E=75°,∴∠E=25°.
24.1.2 垂直于弦的直径要点归纳
知识要点:弦 两条弧 = =
当堂检测
1. A 2. B 3.8 4.6
5.解:(1)如图,作半径OD⊥AB于C,连接 OB.由垂径定理得 在 Rt△OBC中, 0.4=0.1,此时的水深为0.1米.
(2)当水位上升到圆心以下时,水面宽为0.8米,则 水面上升的高度为0.4—0.3=0.1(米);当水位上升到圆心以上时,水面上升的高度为0.4+0.3=0.7(米).综上可得,水面上升的高度为0.1米或0.7 米.
24.1.3 弧、弦、圆心角
要点归纳
知识要点:弧 弦
当堂检测
1. C 2.40 3.(1)60 (2)4
4.50° 5.140 6.8
7.证明: 即(CD=AB,∴AB=CD.
24.1.4 圆周角
要点归纳
知识要点:圆上 相交 一半 相等 直角直径 互补 90° 直径 180°当堂检测
1. C 2.60° 3.140 4.60 8
5.证明:连接AD.∵AB 是直径,∴∠ADB=90°.∴AD⊥BC.∵AB=AC,∴BD=DC, DE.∴BD=DE=DC.
同课章节目录
