沪科版九年级数学上册试题 第23章《解直角三角形》单元检测卷(含答案详解)
文档属性
| 名称 | 沪科版九年级数学上册试题 第23章《解直角三角形》单元检测卷(含答案详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 1007.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-04 16:36:30 | ||
图片预览


文档简介
第23章《解直角三角形》单元检测卷
一、单选题(本大题共10小题,每小题3分,共30分)
1.计算的值为( )
A. B. C. D.
2.在锐角中,若,则等于( )
A. B. C. D.
3.如图,在中,,是边上的中线,若,,则的值为( )
A. B. C. D.
4.一个钢球沿坡角的斜坡向上滚动了5米,此时钢球距地面的高度是(单位:米)( )
A. B. C. D.
5.如图,在平面直角坐标系中,点的坐标为,为第一象限内一点,且.将沿轴向右平移得到与交于点,若,则的面积为( )
A. B. C. D.
6.将三角尺按如图所示的方式放置在一张矩形纸片上,,,,则的度数为( )
A. B. C. D.
7.如图,在中,于点,若,则的值为( )
A. B. C. D.
8.如图,距离地面高m米的A处,用测倾仪测得树顶端C点的仰角为,测得树底端D点的俯角为,则树的高为( )米.
A. B. C. D.
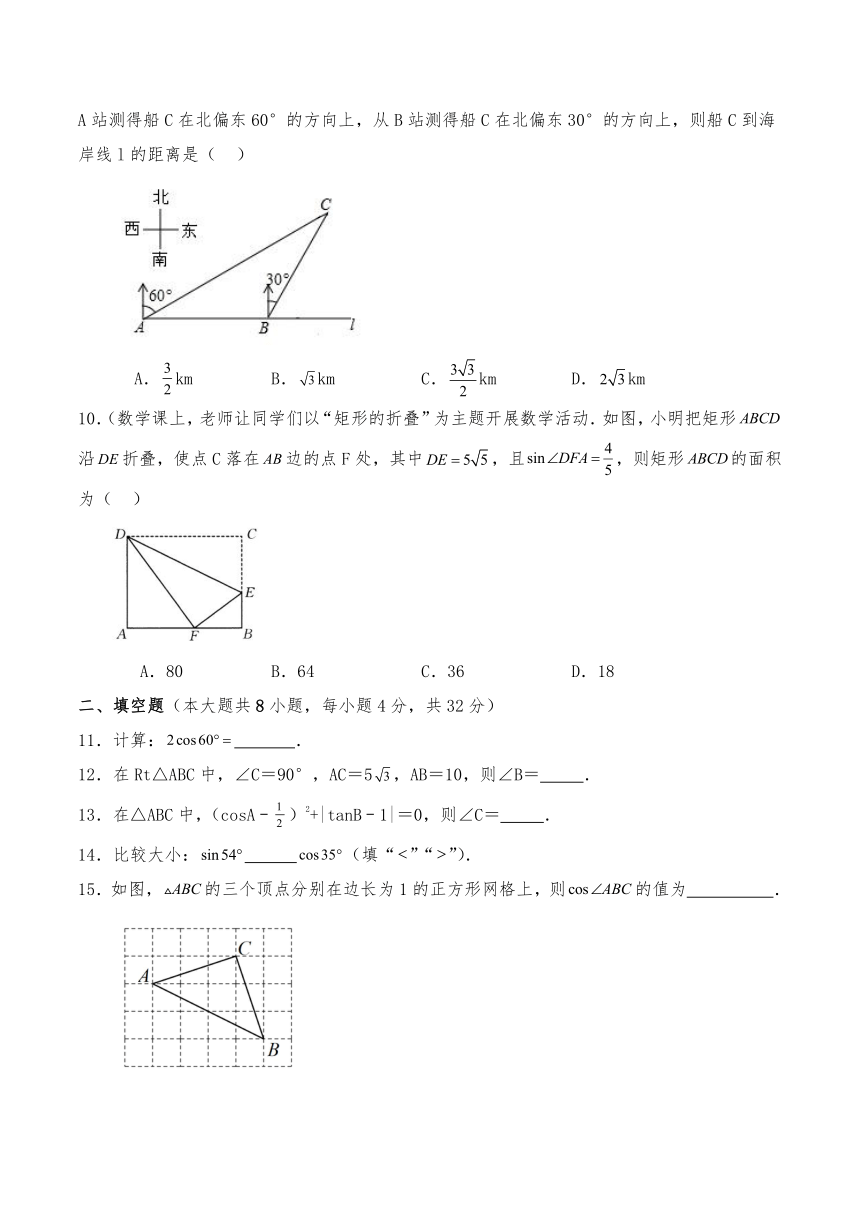
9.如图在一笔直的海岸线l上有相距3km的A,B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60°的方向上,从B站测得船C在北偏东30°的方向上,则船C到海岸线l的距离是( )
A.km B.km C.km D.km
10.(数学课上,老师让同学们以“矩形的折叠”为主题开展数学活动.如图,小明把矩形沿折叠,使点C落在边的点F处,其中,且,则矩形的面积为( )
A.80 B.64 C.36 D.18
二、填空题(本大题共8小题,每小题4分,共32分)
11.计算: .
12.在Rt△ABC中,∠C=90°,AC=5,AB=10,则∠B= .
13.在△ABC中,(cosA﹣)2+|tanB﹣1|=0,则∠C= .
14.比较大小: (填“”“”).
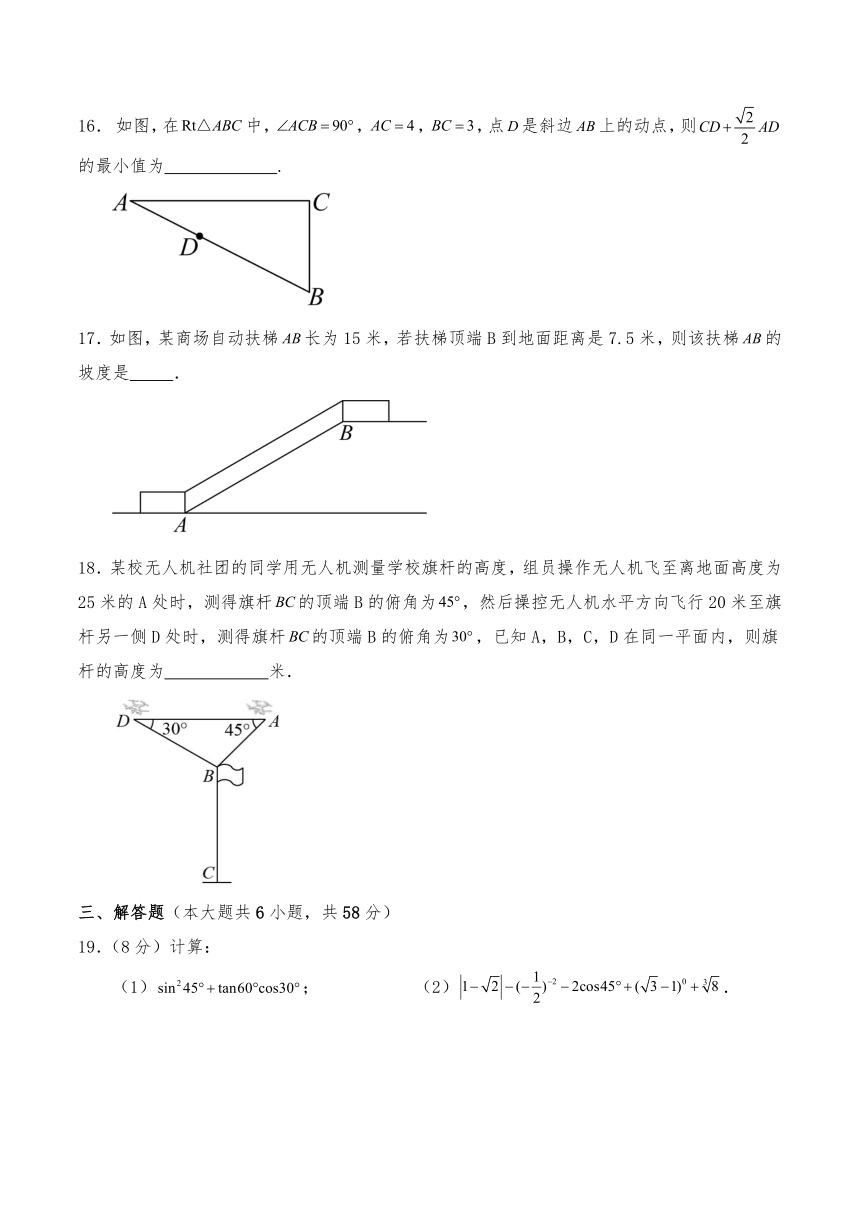
15.如图,的三个顶点分别在边长为1的正方形网格上,则的值为 .
16. 如图,在中,,,,点是斜边上的动点,则的最小值为 .
17.如图,某商场自动扶梯长为15米,若扶梯顶端B到地面距离是7.5米,则该扶梯的坡度是 .
18.某校无人机社团的同学用无人机测量学校旗杆的高度,组员操作无人机飞至离地面高度为25米的A处时,测得旗杆的顶端B的俯角为,然后操控无人机水平方向飞行20米至旗杆另一侧D处时,测得旗杆的顶端B的俯角为,已知A,B,C,D在同一平面内,则旗杆的高度为 米.
三、解答题(本大题共6小题,共58分)
19.(8分)计算:
(1); (2).
20.(8分)先化简,再求代数式的值,其中.
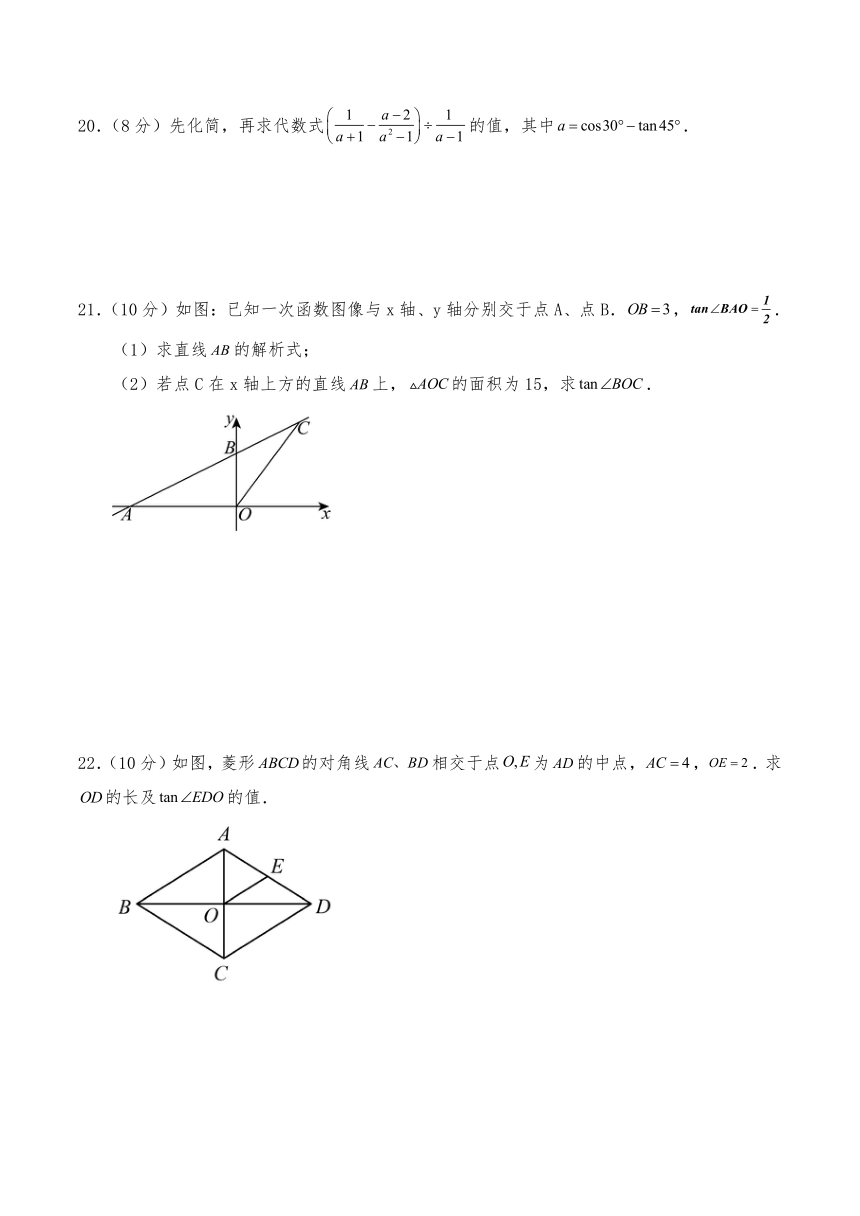
21.(10分)如图:已知一次函数图像与x轴、y轴分别交于点A、点B.,.
(1)求直线的解析式;
(2)若点C在x轴上方的直线上,的面积为15,求.
22.(10分)如图,菱形的对角线相交于点为的中点,,.求的长及的值.
23.(10分)如图,、是两座现代化城市,是一个古城遗址,城在城的北偏东,在城的北偏西,城在城的正东方向,且城与城相距120千米,现在、两城市修建一条笔直的高速公路.
(1)请你计算公路的长度(结果保留根号);
(2)若以为圆心,以60千米为半径的圆形区域内为古迹和地下文物保护区,请你分析公路会不会穿越这个保护区,并说明理由.
24.(12分)如图,,斜坡的长为米,坡度,在点处测得旗杆顶端的仰角为,点到旗杆底部的距离为米.
(1)求斜坡的坡角的度数;
(2)求旗杆顶端离地面的高度的长.(结果精确到0.1米)
答案
一、单选题
1.B
【分析】分别计算三角函数值、零指数幂,化简绝对值,再进行加减即可.
解:
,
故选:B.
2.A
【分析】根据平方及绝对值的非负性可得,,由特殊角的三角函数值求得和,再由三角形内角和为即可解答;
解:∵,
∴,,
∴,,
∴在锐角中,,
故选: A;
3.D
【分析】根据直角三角形斜边上的中线等于斜边的一半可得,再根据等边对等角可得,然后利用锐角的正切值等于对边比邻边列式计算即可得解.
解:∵,是边上的中线,
∴,
∴,
∴.
故选D.
4.B
【分析】铁球上滚的距离,铁球距地面的高度,可看作直角三角形的斜边与已知角的对边,可利用正弦函数求解.
解:铁球上滚的距离铁球距地面的高度,
铁球距地面的高度.
故选:B.
5.C
【分析】由,,得出,根据三角函数求出,根据平移的性质得到,求出,进而得到的长度,再根据三角形面积公式计算.
解:∵,,
∴,
∴,,
∵将沿轴向右平移得到,
∴,
∵,
∴
∴,,
∴,
∴的面积为.
故选:C.
6.B
【分析】根据题意可得,可得,再根据三角形内角和的性质,即可求解.
解:在中,,,
∴,
∴,
由题意可得:,
故选B
7.B
【分析】先根据题目已知条件推出∽,则可得,然后根据,设,,利用对应边成比例表示出的值,进而得出的值,
解:∵在中,,
∴,
∵于点,
∴,
∴,,
∴∽,
∴,即,,
∵,
∴设,,
∴,
∴,
故选:B.
8.A
【分析】如图,根据题意可得,然后再解直角三角形可得,最后根据即可解答.
解:如图:过点A作于E,
由题意可得:,
∵,
∴,
∴.
故选A.
9.C
【分析】首先由题意可证△ACB是等腰三角形,即可求得BC的长,然后由在Rt△CBD中,CD=BC×sin60°,即可求得答案.
解:过C作CD垂直于海岸线l交于D点,
根据题意得∠CAD=90°-60°=30°,∠CBD=90°-30°=60°,
∴∠ACB=∠CBD -∠CAD=30°,
∴∠CAB=∠ACB,
∴BC=AB=3km,
在Rt△CBD中,
CD=BC×sin60°=3×=(km),
故选择:C.
10.A
【分析】首先根据折叠的性质得到,然后根据同角的余角相等得到,进而得到,设,,则,,根据定理求出,,最后利用矩形面积公式求解即可.
解:∵矩形沿折叠,使点C落在边的点F处,
∴,
∴,
∵四边形是矩形,
∴,
∴,
∴,
∴,
∴设,,则,,
∴,
∵,
∴,
∵,,
∴,即,
∴解得:,负值舍去,
∴,,
∴矩形的面积.
故选:A.
二、填空题
11.1
【分析】根据特殊角的三角函数值计算.
解:,
,
故答案为:1.
12.60°
【分析】利用正弦定义计算即可.
解:如图,
∵sinB=,
∴∠B=60°,
故答案为:60°.
13.75°.
【分析】先根据非负数的性质确定cosA=,tanB=1,再根据特殊角的三角函数解答.
解:∵(cosA﹣)2+|tanB﹣1|=0,
∴cosA﹣=0,tanB﹣1=0,
则cosA=,tanB=1,
∴∠A=60°,∠B=45°,
∴∠C=180°﹣60°﹣45°=75°.
故答案为75°.
14.
【分析】把余弦化成正弦,再通过角度大小比较正弦值的大小即可.
解:∵.
在锐角范围内,随的增大而增大,
∴,
∴.
故答案为:<.
15.
【分析】根据,,,得到,推出是直角三角形,,推出.
解:如图,∵,,,
∴,
∴是等腰直角三角形,,
∴,
故答案为:.
16.
【分析】根据两点之间线段最短画出图形,再根据锐角三角函数及相似三角形判定可知,最后利用相似三角形的性质及直角三角形的性质即可解答.
解:过点做,过点作于,过点作于点,
∴,
∴,
∵两点之间线段最短,
∴当共线时,的值最小,
即的最小值为,
∵,,,
∴,
∵,
∴,
∵,
∴,
∴,
∴,,
∵,
∴,
∴,,
∴,
∴,
故答案为.
17.
【分析】根据题意和勾股定理可以求得的长,从而可以解答本题.
解:如图所示,过点B作,
∵自动扶梯长为15米,若扶梯顶端B到地面距离是7.5米,
∴,
该扶梯的坡度是.
故答案为:.
18.
【分析】过点B作于点E,分别在和中,利用锐角三角函数,可得,,再由,可得,即可求解.
解:如图,过点B作于点E,
在中,,
∴,
在中,,
,
∴,
解得:,
∴.
故答案为:
三、解答题
19.
(1)解:原式
;
(2)解:原式
.
20.
解:
;
因为,
∴,
把代入,
得
21.
(1)解:,点B在y轴正半轴上,
,
,
,
点A在x轴的负半轴上,
,
设直线的解析式为,将,代入,得:
,
解得,
直线的解析式为,
(2)解:如图,过点C作轴于点H,则,
,
,
点C的纵坐标为5,
点C在直线上,将代入,得,
解得
点C的横坐标为4,即,
,
,
,
.
22.
解:在菱形中,.
∵,∴.
在中,∵为中点,
∴.
∵.
∴.
∴.
∴.
23.
解:作CD⊥AB于D点.
(1)在Rt△ACD中,
CD=AC sin60°=120×=千米,AD=AC cos60°=120×=60千米,
在Rt△BCD中,BD=CD tan45°=×1=千米,
所以AB=AD+DB=60+(km);
(2)不可能.因为CD=>60,所以不可能对文物古迹造成损毁.
24.
解:(1)∵
∴
(2)作垂足为
在中,
在矩形中
在Rt△BCE中
∴
∴(米)
答:的长是米
一、单选题(本大题共10小题,每小题3分,共30分)
1.计算的值为( )
A. B. C. D.
2.在锐角中,若,则等于( )
A. B. C. D.
3.如图,在中,,是边上的中线,若,,则的值为( )
A. B. C. D.
4.一个钢球沿坡角的斜坡向上滚动了5米,此时钢球距地面的高度是(单位:米)( )
A. B. C. D.
5.如图,在平面直角坐标系中,点的坐标为,为第一象限内一点,且.将沿轴向右平移得到与交于点,若,则的面积为( )
A. B. C. D.
6.将三角尺按如图所示的方式放置在一张矩形纸片上,,,,则的度数为( )
A. B. C. D.
7.如图,在中,于点,若,则的值为( )
A. B. C. D.
8.如图,距离地面高m米的A处,用测倾仪测得树顶端C点的仰角为,测得树底端D点的俯角为,则树的高为( )米.
A. B. C. D.
9.如图在一笔直的海岸线l上有相距3km的A,B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60°的方向上,从B站测得船C在北偏东30°的方向上,则船C到海岸线l的距离是( )
A.km B.km C.km D.km
10.(数学课上,老师让同学们以“矩形的折叠”为主题开展数学活动.如图,小明把矩形沿折叠,使点C落在边的点F处,其中,且,则矩形的面积为( )
A.80 B.64 C.36 D.18
二、填空题(本大题共8小题,每小题4分,共32分)
11.计算: .
12.在Rt△ABC中,∠C=90°,AC=5,AB=10,则∠B= .
13.在△ABC中,(cosA﹣)2+|tanB﹣1|=0,则∠C= .
14.比较大小: (填“”“”).
15.如图,的三个顶点分别在边长为1的正方形网格上,则的值为 .
16. 如图,在中,,,,点是斜边上的动点,则的最小值为 .
17.如图,某商场自动扶梯长为15米,若扶梯顶端B到地面距离是7.5米,则该扶梯的坡度是 .
18.某校无人机社团的同学用无人机测量学校旗杆的高度,组员操作无人机飞至离地面高度为25米的A处时,测得旗杆的顶端B的俯角为,然后操控无人机水平方向飞行20米至旗杆另一侧D处时,测得旗杆的顶端B的俯角为,已知A,B,C,D在同一平面内,则旗杆的高度为 米.
三、解答题(本大题共6小题,共58分)
19.(8分)计算:
(1); (2).
20.(8分)先化简,再求代数式的值,其中.
21.(10分)如图:已知一次函数图像与x轴、y轴分别交于点A、点B.,.
(1)求直线的解析式;
(2)若点C在x轴上方的直线上,的面积为15,求.
22.(10分)如图,菱形的对角线相交于点为的中点,,.求的长及的值.
23.(10分)如图,、是两座现代化城市,是一个古城遗址,城在城的北偏东,在城的北偏西,城在城的正东方向,且城与城相距120千米,现在、两城市修建一条笔直的高速公路.
(1)请你计算公路的长度(结果保留根号);
(2)若以为圆心,以60千米为半径的圆形区域内为古迹和地下文物保护区,请你分析公路会不会穿越这个保护区,并说明理由.
24.(12分)如图,,斜坡的长为米,坡度,在点处测得旗杆顶端的仰角为,点到旗杆底部的距离为米.
(1)求斜坡的坡角的度数;
(2)求旗杆顶端离地面的高度的长.(结果精确到0.1米)
答案
一、单选题
1.B
【分析】分别计算三角函数值、零指数幂,化简绝对值,再进行加减即可.
解:
,
故选:B.
2.A
【分析】根据平方及绝对值的非负性可得,,由特殊角的三角函数值求得和,再由三角形内角和为即可解答;
解:∵,
∴,,
∴,,
∴在锐角中,,
故选: A;
3.D
【分析】根据直角三角形斜边上的中线等于斜边的一半可得,再根据等边对等角可得,然后利用锐角的正切值等于对边比邻边列式计算即可得解.
解:∵,是边上的中线,
∴,
∴,
∴.
故选D.
4.B
【分析】铁球上滚的距离,铁球距地面的高度,可看作直角三角形的斜边与已知角的对边,可利用正弦函数求解.
解:铁球上滚的距离铁球距地面的高度,
铁球距地面的高度.
故选:B.
5.C
【分析】由,,得出,根据三角函数求出,根据平移的性质得到,求出,进而得到的长度,再根据三角形面积公式计算.
解:∵,,
∴,
∴,,
∵将沿轴向右平移得到,
∴,
∵,
∴
∴,,
∴,
∴的面积为.
故选:C.
6.B
【分析】根据题意可得,可得,再根据三角形内角和的性质,即可求解.
解:在中,,,
∴,
∴,
由题意可得:,
故选B
7.B
【分析】先根据题目已知条件推出∽,则可得,然后根据,设,,利用对应边成比例表示出的值,进而得出的值,
解:∵在中,,
∴,
∵于点,
∴,
∴,,
∴∽,
∴,即,,
∵,
∴设,,
∴,
∴,
故选:B.
8.A
【分析】如图,根据题意可得,然后再解直角三角形可得,最后根据即可解答.
解:如图:过点A作于E,
由题意可得:,
∵,
∴,
∴.
故选A.
9.C
【分析】首先由题意可证△ACB是等腰三角形,即可求得BC的长,然后由在Rt△CBD中,CD=BC×sin60°,即可求得答案.
解:过C作CD垂直于海岸线l交于D点,
根据题意得∠CAD=90°-60°=30°,∠CBD=90°-30°=60°,
∴∠ACB=∠CBD -∠CAD=30°,
∴∠CAB=∠ACB,
∴BC=AB=3km,
在Rt△CBD中,
CD=BC×sin60°=3×=(km),
故选择:C.
10.A
【分析】首先根据折叠的性质得到,然后根据同角的余角相等得到,进而得到,设,,则,,根据定理求出,,最后利用矩形面积公式求解即可.
解:∵矩形沿折叠,使点C落在边的点F处,
∴,
∴,
∵四边形是矩形,
∴,
∴,
∴,
∴,
∴设,,则,,
∴,
∵,
∴,
∵,,
∴,即,
∴解得:,负值舍去,
∴,,
∴矩形的面积.
故选:A.
二、填空题
11.1
【分析】根据特殊角的三角函数值计算.
解:,
,
故答案为:1.
12.60°
【分析】利用正弦定义计算即可.
解:如图,
∵sinB=,
∴∠B=60°,
故答案为:60°.
13.75°.
【分析】先根据非负数的性质确定cosA=,tanB=1,再根据特殊角的三角函数解答.
解:∵(cosA﹣)2+|tanB﹣1|=0,
∴cosA﹣=0,tanB﹣1=0,
则cosA=,tanB=1,
∴∠A=60°,∠B=45°,
∴∠C=180°﹣60°﹣45°=75°.
故答案为75°.
14.
【分析】把余弦化成正弦,再通过角度大小比较正弦值的大小即可.
解:∵.
在锐角范围内,随的增大而增大,
∴,
∴.
故答案为:<.
15.
【分析】根据,,,得到,推出是直角三角形,,推出.
解:如图,∵,,,
∴,
∴是等腰直角三角形,,
∴,
故答案为:.
16.
【分析】根据两点之间线段最短画出图形,再根据锐角三角函数及相似三角形判定可知,最后利用相似三角形的性质及直角三角形的性质即可解答.
解:过点做,过点作于,过点作于点,
∴,
∴,
∵两点之间线段最短,
∴当共线时,的值最小,
即的最小值为,
∵,,,
∴,
∵,
∴,
∵,
∴,
∴,
∴,,
∵,
∴,
∴,,
∴,
∴,
故答案为.
17.
【分析】根据题意和勾股定理可以求得的长,从而可以解答本题.
解:如图所示,过点B作,
∵自动扶梯长为15米,若扶梯顶端B到地面距离是7.5米,
∴,
该扶梯的坡度是.
故答案为:.
18.
【分析】过点B作于点E,分别在和中,利用锐角三角函数,可得,,再由,可得,即可求解.
解:如图,过点B作于点E,
在中,,
∴,
在中,,
,
∴,
解得:,
∴.
故答案为:
三、解答题
19.
(1)解:原式
;
(2)解:原式
.
20.
解:
;
因为,
∴,
把代入,
得
21.
(1)解:,点B在y轴正半轴上,
,
,
,
点A在x轴的负半轴上,
,
设直线的解析式为,将,代入,得:
,
解得,
直线的解析式为,
(2)解:如图,过点C作轴于点H,则,
,
,
点C的纵坐标为5,
点C在直线上,将代入,得,
解得
点C的横坐标为4,即,
,
,
,
.
22.
解:在菱形中,.
∵,∴.
在中,∵为中点,
∴.
∵.
∴.
∴.
∴.
23.
解:作CD⊥AB于D点.
(1)在Rt△ACD中,
CD=AC sin60°=120×=千米,AD=AC cos60°=120×=60千米,
在Rt△BCD中,BD=CD tan45°=×1=千米,
所以AB=AD+DB=60+(km);
(2)不可能.因为CD=>60,所以不可能对文物古迹造成损毁.
24.
解:(1)∵
∴
(2)作垂足为
在中,
在矩形中
在Rt△BCE中
∴
∴(米)
答:的长是米
