沪科版九年级数学上册试题 21.1-21.4 二次函数及应用 同步测试(含答案)
文档属性
| 名称 | 沪科版九年级数学上册试题 21.1-21.4 二次函数及应用 同步测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-04 20:14:50 | ||
图片预览


文档简介
21.1-21.4《 二次函数及应用》
一、单选题
1.如图,抛物线的对称轴是.下列结论:①;②;③;④,正确的有( )
A.4个 B.3个 C.2个 D.1个
2.如图,在平面直角坐标系中,二次函数y=x2﹣2x+c的图象与x轴交于A、C两点,与y轴交于点B(0,﹣3),若P是x轴上一动点,点D(0,1)在y轴上,连接PD,则PD+PC的最小值是( )
A.4 B.2+2 C.2 D.
3.在平面直角坐标系中,将抛物线y=x2﹣(m﹣1)x+m(m>1)沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
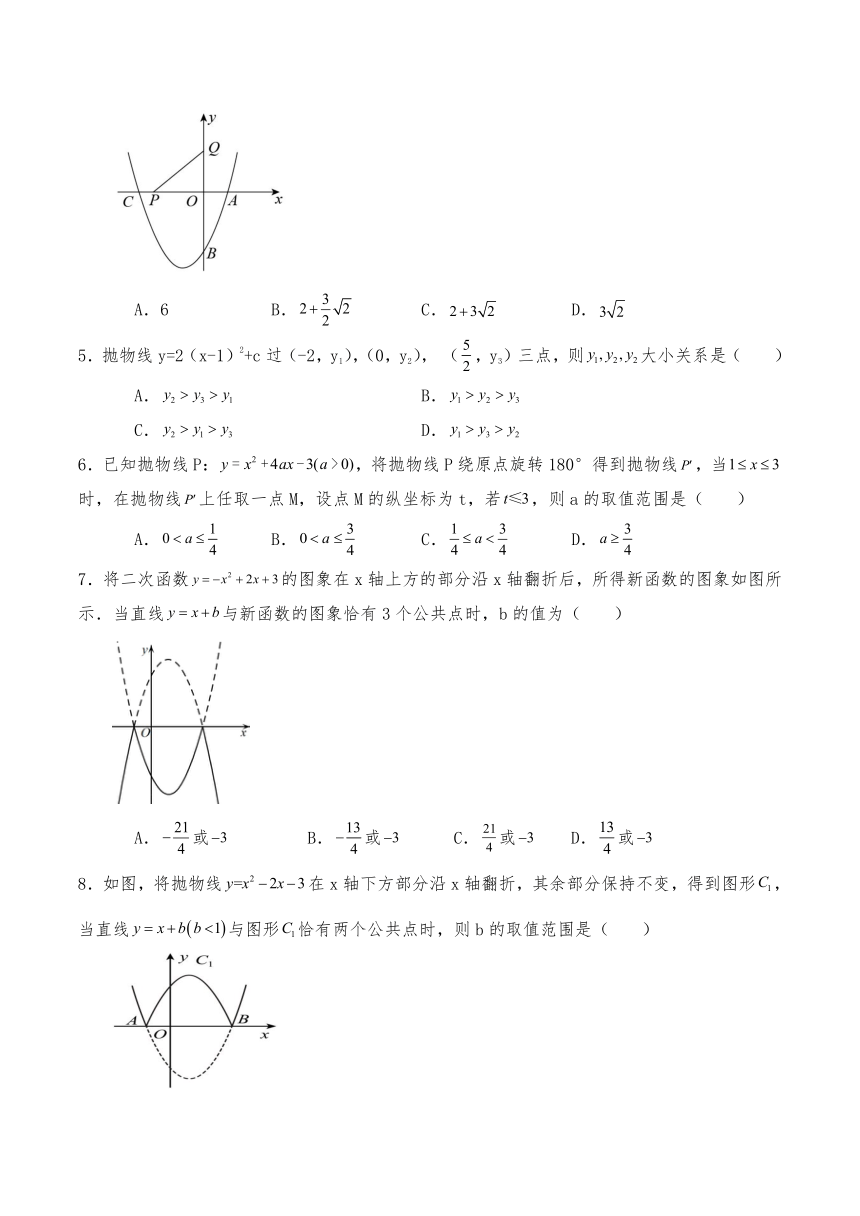
4.如图,在平面直角坐标系中,二次函数的图象与x轴交于A、C两点,与y轴交于点B,若P是x轴上一动点,点Q(0,2)在y轴上,连接PQ,则的最小值是( )
A.6 B. C. D.
5.抛物线y=2(x-1)2+c过(-2,y1),(0,y2), (,y3)三点,则大小关系是( )
A. B.
C. D.
6.已知抛物线P:,将抛物线P绕原点旋转180°得到抛物线,当时,在抛物线上任取一点M,设点M的纵坐标为t,若,则a的取值范围是( )
A. B. C. D.
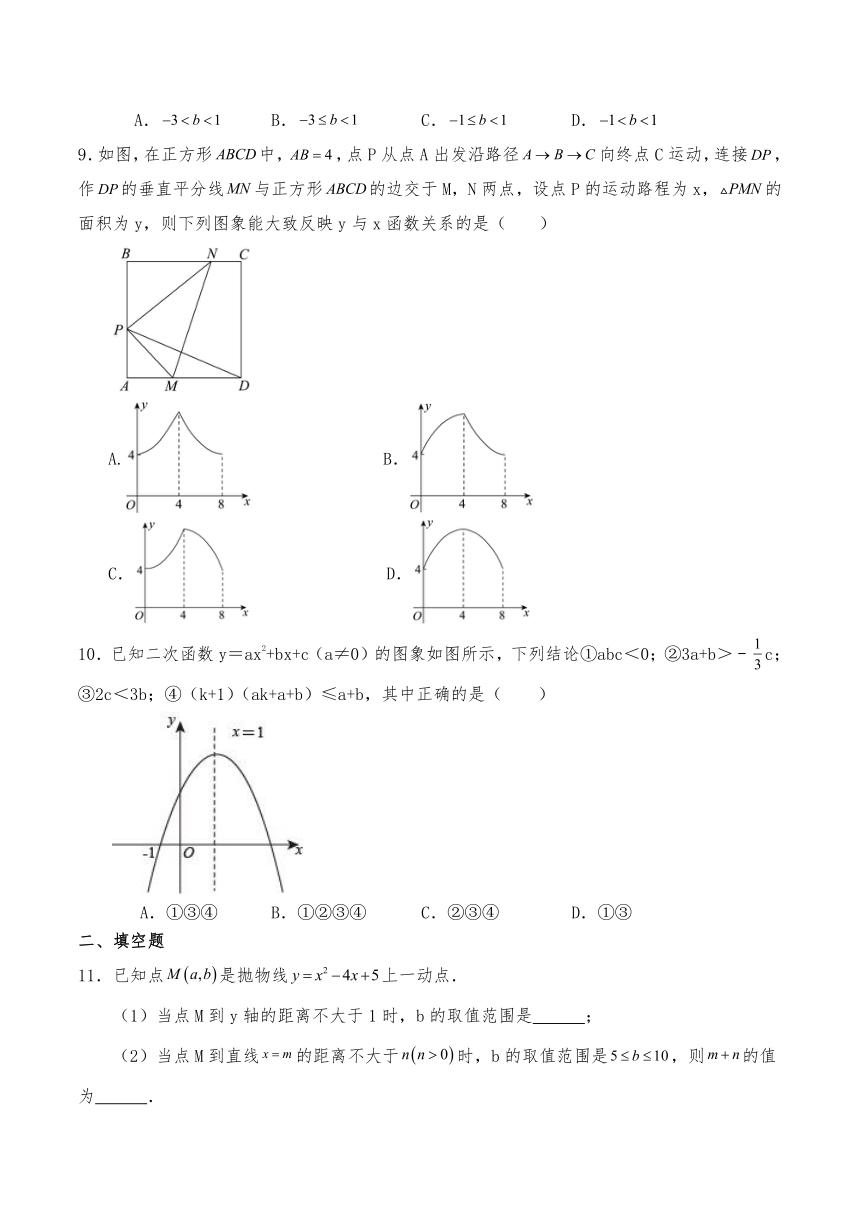
7.将二次函数的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线与新函数的图象恰有3个公共点时,b的值为( )
A.或 B.或 C.或 D.或
8.如图,将抛物线在x轴下方部分沿x轴翻折,其余部分保持不变,得到图形,当直线与图形恰有两个公共点时,则b的取值范围是( )
A. B. C. D.
9.如图,在正方形中,,点P从点A出发沿路径向终点C运动,连接,作的垂直平分线与正方形的边交于M,N两点,设点P的运动路程为x,的面积为y,则下列图象能大致反映y与x函数关系的是( )
A. B.
C. D.
10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论①abc<0;②3a+b>﹣c;③2c<3b;④(k+1)(ak+a+b)≤a+b,其中正确的是( )
A.①③④ B.①②③④ C.②③④ D.①③
二、填空题
11.已知点是抛物线上一动点.
(1)当点M到y轴的距离不大于1时,b的取值范围是 ;
(2)当点M到直线的距离不大于时,b的取值范围是,则的值为 .
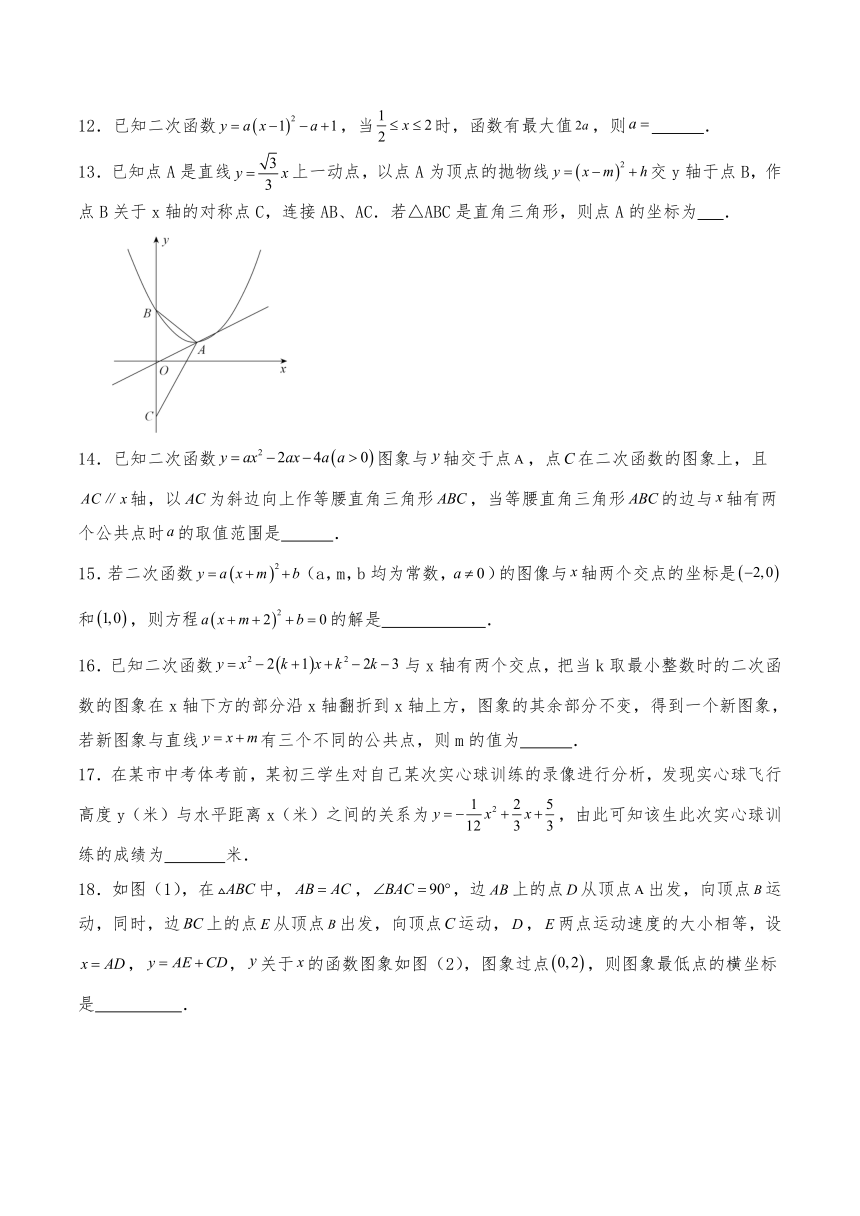
12.已知二次函数,当时,函数有最大值,则 .
13.已知点A是直线上一动点,以点A为顶点的抛物线交y轴于点B,作点B关于x轴的对称点C,连接AB、AC.若△ABC是直角三角形,则点A的坐标为 .
14.已知二次函数图象与轴交于点,点在二次函数的图象上,且轴,以为斜边向上作等腰直角三角形,当等腰直角三角形的边与轴有两个公共点时的取值范围是 .
15.若二次函数(a,m,b均为常数,)的图像与轴两个交点的坐标是和,则方程的解是 .
16.已知二次函数与x轴有两个交点,把当k取最小整数时的二次函数的图象在x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分不变,得到一个新图象,若新图象与直线有三个不同的公共点,则m的值为 .
17.在某市中考体考前,某初三学生对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为,由此可知该生此次实心球训练的成绩为 米.
18.如图(1),在中,,,边上的点从顶点出发,向顶点运动,同时,边上的点从顶点出发,向顶点运动,,两点运动速度的大小相等,设,,关于的函数图象如图(2),图象过点,则图象最低点的横坐标是 .
三、解答题
19.如图,抛物线与x轴交于点,点,与y轴交于点C.
(1)求抛物线的表达式;
(2)在对称轴上找一点Q,使的周长最小,求点Q的坐标;
(3)点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,当是以为腰的等腰直角三角形时,请直接写出所有点M的坐标.
20.若二次函数的图象经过点,,其对称轴为直线,与x轴的另一交点为C.
(1)求二次函数的表达式;
(2)若点M在直线上,且在第四象限,过点M作轴于点N.
①若点N在线段上,且,求点M的坐标;
②以为对角线作正方形(点P在右侧),当点P在抛物线上时,求点M的坐标.
21.如图,在平面直角坐标系中,已知抛物线经过,,三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,的面积为S,求S关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线上的动点,判断有几个位置能使以点P,Q,B,O为顶点的四边形为平行四边形(要求),直接写出相应的点Q的坐标.
22.如图,已知抛物线的对称轴为直线,且抛物线与轴交于、两点,与轴交于点,其中,.
(1)若直线经过、两点,求直线和抛物线的解析式;
(2)在抛物线的对称轴上找一点,使点到点的距离与到点的距离之和最小,求出点的坐标;
(3)设点为抛物线的对称轴上的一个动点,求使为直角三角形的点的坐标.
23.为增强民众生活幸福感,市政府大力推进老旧小区改造工程.和谐小区新建一小型活动广场,计划在360m2的绿化带上种植甲乙两种花卉.市场调查发现:甲种花卉种植费用y(元/m2)与种植面积x(m2)之间的函数关系如图所示,乙种花卉种植费用为15元/m2.
(1)当x≤100时,求y与x的函数关系式,并写出x的取值范围;
(2)当甲种花卉种植面积不少于30m2,且乙种花卉种植面积不低于甲种花卉种植面积的3倍时.
①如何分配甲乙两种花卉的种植面积才能使种植的总费用w(元)最少?最少是多少元?
②受投入资金的限制,种植总费用不超过6000元,请直接写出甲种花卉种植面积x的取值范围.
24.已知抛物线过点.
(1)求抛物线的解析式;
(2)点A在直线上且在第一象限内,过A作轴于B,以为斜边在其左侧作等腰直角.
①若A与Q重合,求C到抛物线对称轴的距离;
②若C落在抛物线上,求C的坐标.
答案
一、单选题
1.B
【分析】由抛物线的性质和对称轴是,分别判断a、b、c的符号,即可判断①;抛物线与x轴有两个交点,可判断②;由,得,令,求函数值,即可判断③;令时,则,令时,,即可判断④;然后得到答案.
解:根据题意,则,,
∵,
∴,
∴,故①错误;
由抛物线与x轴有两个交点,则,故②正确;
∵,
令时,,
∴,故③正确;
在中,
令时,则,
令时,,
由两式相加,得,故④正确;
∴正确的结论有:②③④,共3个;
故选:B.
2.A
【分析】过点P作PJ⊥BC于J,过点D作DH⊥BC于H.根据,求出的最小值即可解决问题.
解:过点P作PJ⊥BC于J,过点D作DH⊥BC于H.
∵二次函数y=x2﹣2x+c的图象与y轴交于点B(0,﹣3),
∴c=﹣3,
∴二次函数的解析式为y=x2﹣2x﹣3,令y=0,x2﹣2x﹣3=0,
解得x=﹣1或3,
∴A(﹣1,0),B(0,-3),
∴OB=OC=3,
∵∠BOC=90°,
∴∠OBC=∠OCB=45°,
∵D(0,1),
∴OD=1,BD=4,
∵DH⊥BC,
∴∠DHB=90°,
设,则,
∵,
∴,
∴,
∴,
∵PJ⊥CB,
∴,
∴,
∴,
∵,
∴,
∴DP+PJ的最小值为,
∴的最小值为4.
故选:A.
3.D
【分析】根据平移规律得到平移后抛物线的顶点坐标,然后结合的取值范围判断新抛物线的顶点所在的象限即可.
解:,
该抛物线顶点坐标是,,
将其沿轴向下平移3个单位后得到的抛物线的顶点坐标是,,
,
,
,
,
点,在第四象限;
故选:.
4.D
【分析】连接,过点P作PD⊥BC于D,过点Q作QH⊥BC于H.根据,可得的最小值为的长,即可解决问题.
解:如图,连接,过点P作PD⊥BC于D,过点Q作QH⊥BC于H.
由,令,则,
解得,
,
令,解得,
,
,
,
,
,
,
当为与轴交点时最小,最小值为的长,
Q(0,2),,
,
设,则,
∵,
∴,
∴,
∴,
则的最小值是.
故选D.
5.D
【分析】由题意可知抛物线开口向上,对称轴是直线x=1,求出(,y3) 直线x=1的对称点,然后根据二次函数的增减性可以判断y1,y2,y3的大小关系,从而可以解答本题.
解:∵y=2(x-1)2+c,2>0,
∴抛物线开口向上,对称轴是直线x=1,
∴当x<1时,y随x的增大而减小;(,y3)关于直线x=1的对称点是(,y3),
∵-2<<0<1
∴y1>y3>y2,
故选D.
6.A
【分析】先求出抛物线的解析式,再列出不等式,求出其解集或,从而可得当x=1时,,有成立,最后求出a的取值范围.
解:∵抛物线P:,将抛物线P绕原点旋转180°得到抛物线,
∴抛物线P与抛物线关于原点对称,
设点(x,y)在抛物线P’上,则点(-x,-y)一定在抛物线P上,
∴
∴抛物线的解析式为,
∵当时,在抛物线上任取一点M,设点M的纵坐标为t,若,
即
令,
∴,
解得:或,
设,
∵开口向下,且与x轴的两个交点为(0,0),(4a,0),
即当时,要恒成立,此时,
∴当x=1时,即可,
得:,
解得:,
又∵
∴
故选A
7.A
【分析】由二次函数解析式,可求与x轴的两个交点A、B,直线表示的图像可看做是直线的图像平移b个单位长度得到,再结合所给函数图像可知,当平移直线经过B点时,恰与所给图像有三个交点,故将B点坐标代入即可求解;当平移直线经过C点时,恰与所给图像有三个交点,即直线与函数关于x轴对称的函数图像只有一个交点,即联立解析式得到的方程的判别式等于0,即可求解.
解:由知,当时,即
解得:
作函数的图像并平移至过点B时,恰与所给图像有三个交点,此时有:
平移图像至过点C时,恰与所给图像有三个交点,即当时,只有一个交点
当的函数图像由的图像关于x轴对称得到
当时对应的解析式为
即,整理得:
综上所述或
故答案是:A.
8.A
【分析】通过解方程x2 2x 3=0得到A、B的坐标,利用二次函数的性质得到顶点的坐标,可写出图象y=(x 1)2 4( 1解:当y=0时,x2 2x 3=0,解得x1= 1,x2=3,则A( 1,0),B(3,0),
y=x2 2x 3=(x 1)2 4,则顶点坐标为(1, 4),
把图象y=(x 1)2 4( 1如图,
当直线y=x+b与y= x2+2x+3( 1方程整理得x2 x+b 3=0,,解得,
,
舍去;
当直线y=x+b过A( 1,0)时, 1+b=0,解得b=1,
当直线y=x+b过B(3,0)时,3+b=0,解得b= 3,
所以,当 3故选:A.
9.A
【分析】分点P在AB和BC上两种情况,分别求出MN和PF长,利用面积公式求解.
解:(1)如图,当0≤x≤4时,点P在AB上,过点N作NE⊥AD于点E,设MN与PD交于点F,
∴NE=DC=AD,
则PD= ,
又∵MN垂直平分PD,
∴PF= ,
∴∠MDF+∠FMD=∠MNE+∠FME=90°,
∴∠MNE=∠PDA,
在△MNE和△PDA中,
∴△APD≌△EMN,
∴PD=MN= ,
∴y= ,
(2)如图,当4<x≤8时,点P在BC上,
过点N作NE⊥CD于点E,设MN交PD于点F,
则PD= ,
∴PF
用(1)的方法得
MN,
y=,
故
故选择A.
10.A
【分析】根据二次函数图象与性质,逐项判断即可.
解:∵抛物线开口向下,
∴a<0,
∵对称轴是直线x=1,
∴﹣=1,即b=﹣2a,
∴b>0,
∵抛物线与y轴交点在正半轴,
∴c>0,
∴abc<0,故①正确;
由图象可知,x=3时y<0,
∴9a+3b+c<0,
∴3a+b<﹣c,故②错误;
∵9a+3b+c<0,b=﹣2a,
∴﹣b+3b+c<0,
∴2c<3b,故③正确,
∵x=1时,y=a+b+c是函数的最大值,
∴a(k+1)2+b(k+1)+c≤a+b+c,
∴a(k+1)2+b(k+1)≤a+b,
∴(k+1)(ak+a+b)≤a+b,
故④正确,
∴正确的有①③④,
故选:A.
二、填空题
11. / 0或5/5或0
【分析】(1)先求出抛物线的对称轴为直线,根据点M到y轴的距离不大于1,得出,根据二次函数的增减性,求出b的取值范围即可;
(2)根据点到直线的距离不大于,得出,即,从而得出,然后根据,求出a的范围,即可得出.
解:(1)∵,
∴抛物线的对称轴为直线,
∵点M到y轴的距离不大于1,
∴,
∴此时点M在对称轴的左侧,
∵,
∴在对称轴的左侧随x的增大而减小,
∴当时,b取最大值,且最大值为,
当时,b取最小值,且最小值为,
∴b的取值范围是;
故答案为:;
(2)∵点到直线的距离不大于,
∴,即,
∴,
令,代入,即,解得:,,
令,代入,即,解得:,,
∴点M应为或上的动点,
当时,,
当时,,
综上分析可知,的值为0或5;
故答案为:0或5.
12.
【分析】根据二次函数的性质,可以得到该函数的对称轴,然后再根据当时,函数有最大值,即可得到关于的方程,然后求解即可.
解:∵二次函数,
∴该函数图像对称轴是直线,
当时,当时,该函数取到最大值,
∵当时,函数有最大值,
∴,
解得:(不合题意,舍去);
当时,当时,该函数取到最小值,
当时,
当时,,
当时,,
根据二次函数对称的性质可知:当时,函数有最大值,
又∵当时,函数有最大值,
∴,
解得.
故答案为:.
13.或或
【分析】分两种情况:∠BAC=90°,则由题意得OA=OB,从而得到关于m的方程,解方程即可;∠ACB=90°,则点A、C的纵坐标相同,可得关于m的方程,解方程即可.
解:由题意得:A(m,h),且,
上式中令x=0,得,
∴.
∵点A在直线上,
∴,
即,,
∵点B、点C关于x轴的对称,
则.
①当∠BAC=90°,则OA是Rt△ABC的斜边BC上的中线,
∴OA=OB,
∵,,
则,
由于m≠0,
解得:或,
所以点A的坐标为或;
②当∠ACB=90°时,如图,则AC⊥BC,此时点A、C的纵坐标相同,
即,
∴,m=0(舍去),
所以点A的坐标为;
综上所述,点A的坐标为或或.
14.
【分析】过点B作BD⊥AC于D.根据二次函数的解析式和对称性求出OA和AC的长度,再根据等腰三角形的性质和等角对等边求出BD的长度,最后通过数形结合思想确定OA解:如下图所示,过点B作BD⊥AC于D.
∵二次函数的解析式为,
∴当x=0时,y=-4a,二次函数的对称轴是直线.
∴.
∴OA=4a.
∵点在二次函数的图象上,且轴,
∴点A与点C关于直线x=1对称.
∴.
∴AC=2.
∵△ABC是等腰直角三角形,AC为斜边,BD⊥AC,
∴∠BAD=45°,∠BDA=90°,AD=CD=.
∴∠ABD=45°.
∴∠BAD=∠ABD.
∴BD=AD=1.
∵等腰直角三角形的边与轴有两个公共点,
∴OA∴4a<1.
∴.
∵a>0,
∴.
故答案为:.
15.,
【分析】根据抛物线y=a(x+m)2+b与x轴的两交点为(-2,0),(1,0),得出方程a(x+m)2+b=0的解,然后根据方程a(x+m)2+b=0的解与a(x+m+2)2+b=0的解的关系得出答案即可.
解:∵抛物线y=a(x+m)2+b与x轴的两交点为(-2,0),(1,0),
∴方程a(x+m)2+b=0的解为x1=-2,x2=1,
∴方程a(x+m+2)2+b=0中,x+2=-2或x+2=1,
∴方程a(x+m+2)2+b=0的解为x1=-4,x2=-1.
故答案为:x1=-4,x2=-1.
16.1或
【分析】先运用根的判别式求得k的取值范围,进而确定k的值,得到抛物线的解析式,再根据折叠得到新图像的解析式,可求出函数图象与x轴的交点坐标,画出函数图象,可发现,若直线与新函数有3个交点,可以有两种情况:①过交点(-1,0),根据待定系数法可得m的值;②不过点(一1,0),与相切时,根据判别式解答即可.
解:∵函数与x轴有两个交点,
∴,解得,
当k取最小整数时,,
∴抛物线为,
将该二次函数图象在x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分不变,得到一个新图象,所以新图象的解析式为(或) :
①因为为的,所以它的图象从左到右是上升的,当它与新图象有3个交点时它一定过,把代入得所以,
②与相切时,图象有三个交点,
,,解得.
故答案为:1或.
17.10
【分析】根据铅球落地时,高度,把实际问题可理解为当时,求x的值即可.
解:当时,,
解得,(舍去),.
故答案为10.
18.
【分析】先根据图形可知AE+CD=AB+AC=2,进而求得AB=AC=1、BC=以及图象最低点的函数值即为AE+CD的最小值;再运用勾股定理求得CD、AE,然后根据AE+CD得到+可知其表示点(x,0)到(0,-1)与(,)的距离之和,然后得当三点共线时有函数值.最后求出该直线的解析式,进而求得x的值.
解:由图可知,当x=0时,AE+CD=AB+AC=2
∴AB=AC=1,BC=,图象最低点函数值即为AE+CD的最小值
由题意可得:CD=,AE=
∴AE+CD=+,即点(x,0)到(0,-1)与(,)的距离之和
∴当这三点共线时,AE+CD最小
设该直线的解析式为y=kx+b
解得
∴
当y=0时,x=.
故填.
三、解答题
19.
(1)解:∵抛物线与x轴交于点,点,
∴,
∴,
∴抛物线解析式为;
(2)解:∵抛物线解析式为,与y轴交于点C,
∴抛物线对称轴为直线,点C的坐标为(0,-3)
如图所示,作点C关于直线的对称点E,连接AE,EQ,则点E的坐标为(2,-3),
由轴对称的性质可知CQ=EQ,
∴△ACQ的周长=AC+AQ+CQ,
要使△ACQ的周长最小,则AQ+CQ最小,即AQ+QE最小,
∴当A、Q、E三点共线时,AQ+QE最小,
设直线AE的解析式为,
∴,
∴,
∴直线AE的解析式为,
当时,,
∴点Q的坐标为(1,-2);
(3)解: 如图1所示,当点P在x轴上方,∠BPM=90°时,过点P作轴,过点M作MF⊥EF于F,过点B作BE⊥EF于E,
∵△PBM是以PB为腰的等腰直角三角形,
∴PA=PB,∠MFP=∠PEB=∠BPM=90°,
∴∠FMP+∠FPM=∠FPM+∠EPB=90°,
∴∠FMP=∠EPB,
∴△FMP≌△EPB(AAS),
∴PE=MF,BE=PF,
设点P的坐标为(1,m),
∴,
∴,,
∴点M的坐标为(1-m,m-2),
∵点M在抛物线上,
∴,
∴,
∴,
解得或(舍去),
∴点M的坐标为(-1,0);
同理当当点P在x轴下方,∠BPM=90°时可以求得点M的坐标为(-1,0);
如图2所示,当点P在x轴上方,∠PBM=90°时,过点B作轴,过点P作PE⊥EF于E,过点M作MF⊥EF于F,设点P的坐标为(1,m),
同理可证△PEB≌△BFM(AAS),
∴,
∴点M的坐标为(3-m,-2),
∵点M在抛物线上,
∴,
∴,
∴,
解得或(舍去),
∴点M的坐标为(,-2);
如图3所示,当点P在x轴下方,∠PBM=90°时,
同理可以求得点M的坐标为(,2);
综上所述,当△PMB是以PB为腰的等腰直角三角形时,点M的坐标为(-1,0)或(,-2)或(,2).
20.
(1)解:二次函数的图象经过点,
.
又抛物线经过点,对称轴为直线,
解得∶
抛物线的表达式为.
(2)解∶①设直线的表达式为.
点A,B的坐标为,,
∴, 解得: ,
直线的表达式为.
根据题意得:点C与点关于对称轴直线对称,
.
设点N的坐标为.
轴,
.
∴
.
,
解,得.
点M的坐标;
②连接与交与点E.
设点M的坐标为,则点N的坐标为
四边形是正方形,
,,.
∵MN⊥x轴,
轴.
E的坐标为.
.
.
∴P的坐标.
点P在抛物线上,
.
解,得,.
点P在第四象限,
舍去.
即.
点M坐标为.
21.
(1)解:设此抛物线的函数解析式为:,
将,,三点代入函数解析式得:
,
解得,
所以此函数解析式为:;
(2)解:连接 ,
∵M点的横坐标为m,且点M在这条抛物线上,
∴M点的坐标为,
∴
,
∵,
当时,S有最大值为:.
(3)解:设,
根据平行四边形的性质知,且,则,为平行四边形的边,
∴Q的横坐标等于P的横坐标,
又∵直线的解析式为,
则,
由,得,
整理得:
所以或
解得或或(不符合题意,舍去),
∵,
∴不可能是对角线
∴由此可得:或或.
22.
详解:(1)依题意得:,解得:,
∴抛物线的解析式为.
∵对称轴为,且抛物线经过,
∴把、分别代入直线,
得,解之得:,
∴直线的解析式为.
(2)直线与对称轴的交点为,则此时的值最小,把代入直线得,
∴.即当点到点的距离与到点的距离之和最小时的坐标为.
(注:本题只求坐标没说要求证明为何此时的值最小,所以答案未证明的值最小的原因).
(3)设,又,,
∴,,,
①若点为直角顶点,则,即:解得:,
②若点为直角顶点,则,即:解得:,
③若点为直角顶点,则,即:解得:
,.
综上所述的坐标为或或或.
23.解:(1)由图像可知,当甲种花卉种植面积m2时,费用y保持不变,为30(元/m2),
所以此区间的函数关系式为:,
当甲种花卉种植面积m2时,函数图像为直线,
设函数关系式为:,
∵当x=40时,y=30,当x=100时,y=15,代入函数关系式得:
,
解得:,
∴
∴当时,y与x的函数关系式应为:
;
(2)∵甲种花卉种植面积不少于30m2,
∵乙种花卉种植面积不低于甲种花卉种植面积的3倍,
,
即,
①当时,
由(1)知,,
∵乙种花卉种植费用为15元/m2.
,
∴当x=90时,,
,
∴种植甲种花卉90m2,乙种花卉270m2时,种植的总费用最少,最少为5625元;
②当时,
由①知,,
∵种植总费用不超过6000元,,
,
即满足条件的x的范围为,
当时,
由①知,,
∵种植总费用不超过6000元,
,
(不符合题意,舍去)或,
即满足条件的x的范围为
综上,满足条件的x的范围为或.
24.解:(1)将两点分别代入,得
解得.
所以抛物线的解析式是.
(2)①如图2,抛物线的对称轴是y轴,当点A与点重合时,,
作于H.
∵是等腰直角三角形,
∴和也是等腰直角三角形,
∴,
∴点C到抛物线的对称轴的距离等于1.
②如图3,设直线PQ的解析式为y=kx+b,由,得
解得
∴直线的解析式为,
设,
∴,
所以.
所以.
将点代入,
得.
整理,得.
因式分解,得.
解得,或(与点P重合,舍去).
当时,.
所以点C的坐标是.
一、单选题
1.如图,抛物线的对称轴是.下列结论:①;②;③;④,正确的有( )
A.4个 B.3个 C.2个 D.1个
2.如图,在平面直角坐标系中,二次函数y=x2﹣2x+c的图象与x轴交于A、C两点,与y轴交于点B(0,﹣3),若P是x轴上一动点,点D(0,1)在y轴上,连接PD,则PD+PC的最小值是( )
A.4 B.2+2 C.2 D.
3.在平面直角坐标系中,将抛物线y=x2﹣(m﹣1)x+m(m>1)沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.如图,在平面直角坐标系中,二次函数的图象与x轴交于A、C两点,与y轴交于点B,若P是x轴上一动点,点Q(0,2)在y轴上,连接PQ,则的最小值是( )
A.6 B. C. D.
5.抛物线y=2(x-1)2+c过(-2,y1),(0,y2), (,y3)三点,则大小关系是( )
A. B.
C. D.
6.已知抛物线P:,将抛物线P绕原点旋转180°得到抛物线,当时,在抛物线上任取一点M,设点M的纵坐标为t,若,则a的取值范围是( )
A. B. C. D.
7.将二次函数的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线与新函数的图象恰有3个公共点时,b的值为( )
A.或 B.或 C.或 D.或
8.如图,将抛物线在x轴下方部分沿x轴翻折,其余部分保持不变,得到图形,当直线与图形恰有两个公共点时,则b的取值范围是( )
A. B. C. D.
9.如图,在正方形中,,点P从点A出发沿路径向终点C运动,连接,作的垂直平分线与正方形的边交于M,N两点,设点P的运动路程为x,的面积为y,则下列图象能大致反映y与x函数关系的是( )
A. B.
C. D.
10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论①abc<0;②3a+b>﹣c;③2c<3b;④(k+1)(ak+a+b)≤a+b,其中正确的是( )
A.①③④ B.①②③④ C.②③④ D.①③
二、填空题
11.已知点是抛物线上一动点.
(1)当点M到y轴的距离不大于1时,b的取值范围是 ;
(2)当点M到直线的距离不大于时,b的取值范围是,则的值为 .
12.已知二次函数,当时,函数有最大值,则 .
13.已知点A是直线上一动点,以点A为顶点的抛物线交y轴于点B,作点B关于x轴的对称点C,连接AB、AC.若△ABC是直角三角形,则点A的坐标为 .
14.已知二次函数图象与轴交于点,点在二次函数的图象上,且轴,以为斜边向上作等腰直角三角形,当等腰直角三角形的边与轴有两个公共点时的取值范围是 .
15.若二次函数(a,m,b均为常数,)的图像与轴两个交点的坐标是和,则方程的解是 .
16.已知二次函数与x轴有两个交点,把当k取最小整数时的二次函数的图象在x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分不变,得到一个新图象,若新图象与直线有三个不同的公共点,则m的值为 .
17.在某市中考体考前,某初三学生对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为,由此可知该生此次实心球训练的成绩为 米.
18.如图(1),在中,,,边上的点从顶点出发,向顶点运动,同时,边上的点从顶点出发,向顶点运动,,两点运动速度的大小相等,设,,关于的函数图象如图(2),图象过点,则图象最低点的横坐标是 .
三、解答题
19.如图,抛物线与x轴交于点,点,与y轴交于点C.
(1)求抛物线的表达式;
(2)在对称轴上找一点Q,使的周长最小,求点Q的坐标;
(3)点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,当是以为腰的等腰直角三角形时,请直接写出所有点M的坐标.
20.若二次函数的图象经过点,,其对称轴为直线,与x轴的另一交点为C.
(1)求二次函数的表达式;
(2)若点M在直线上,且在第四象限,过点M作轴于点N.
①若点N在线段上,且,求点M的坐标;
②以为对角线作正方形(点P在右侧),当点P在抛物线上时,求点M的坐标.
21.如图,在平面直角坐标系中,已知抛物线经过,,三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,的面积为S,求S关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线上的动点,判断有几个位置能使以点P,Q,B,O为顶点的四边形为平行四边形(要求),直接写出相应的点Q的坐标.
22.如图,已知抛物线的对称轴为直线,且抛物线与轴交于、两点,与轴交于点,其中,.
(1)若直线经过、两点,求直线和抛物线的解析式;
(2)在抛物线的对称轴上找一点,使点到点的距离与到点的距离之和最小,求出点的坐标;
(3)设点为抛物线的对称轴上的一个动点,求使为直角三角形的点的坐标.
23.为增强民众生活幸福感,市政府大力推进老旧小区改造工程.和谐小区新建一小型活动广场,计划在360m2的绿化带上种植甲乙两种花卉.市场调查发现:甲种花卉种植费用y(元/m2)与种植面积x(m2)之间的函数关系如图所示,乙种花卉种植费用为15元/m2.
(1)当x≤100时,求y与x的函数关系式,并写出x的取值范围;
(2)当甲种花卉种植面积不少于30m2,且乙种花卉种植面积不低于甲种花卉种植面积的3倍时.
①如何分配甲乙两种花卉的种植面积才能使种植的总费用w(元)最少?最少是多少元?
②受投入资金的限制,种植总费用不超过6000元,请直接写出甲种花卉种植面积x的取值范围.
24.已知抛物线过点.
(1)求抛物线的解析式;
(2)点A在直线上且在第一象限内,过A作轴于B,以为斜边在其左侧作等腰直角.
①若A与Q重合,求C到抛物线对称轴的距离;
②若C落在抛物线上,求C的坐标.
答案
一、单选题
1.B
【分析】由抛物线的性质和对称轴是,分别判断a、b、c的符号,即可判断①;抛物线与x轴有两个交点,可判断②;由,得,令,求函数值,即可判断③;令时,则,令时,,即可判断④;然后得到答案.
解:根据题意,则,,
∵,
∴,
∴,故①错误;
由抛物线与x轴有两个交点,则,故②正确;
∵,
令时,,
∴,故③正确;
在中,
令时,则,
令时,,
由两式相加,得,故④正确;
∴正确的结论有:②③④,共3个;
故选:B.
2.A
【分析】过点P作PJ⊥BC于J,过点D作DH⊥BC于H.根据,求出的最小值即可解决问题.
解:过点P作PJ⊥BC于J,过点D作DH⊥BC于H.
∵二次函数y=x2﹣2x+c的图象与y轴交于点B(0,﹣3),
∴c=﹣3,
∴二次函数的解析式为y=x2﹣2x﹣3,令y=0,x2﹣2x﹣3=0,
解得x=﹣1或3,
∴A(﹣1,0),B(0,-3),
∴OB=OC=3,
∵∠BOC=90°,
∴∠OBC=∠OCB=45°,
∵D(0,1),
∴OD=1,BD=4,
∵DH⊥BC,
∴∠DHB=90°,
设,则,
∵,
∴,
∴,
∴,
∵PJ⊥CB,
∴,
∴,
∴,
∵,
∴,
∴DP+PJ的最小值为,
∴的最小值为4.
故选:A.
3.D
【分析】根据平移规律得到平移后抛物线的顶点坐标,然后结合的取值范围判断新抛物线的顶点所在的象限即可.
解:,
该抛物线顶点坐标是,,
将其沿轴向下平移3个单位后得到的抛物线的顶点坐标是,,
,
,
,
,
点,在第四象限;
故选:.
4.D
【分析】连接,过点P作PD⊥BC于D,过点Q作QH⊥BC于H.根据,可得的最小值为的长,即可解决问题.
解:如图,连接,过点P作PD⊥BC于D,过点Q作QH⊥BC于H.
由,令,则,
解得,
,
令,解得,
,
,
,
,
,
,
当为与轴交点时最小,最小值为的长,
Q(0,2),,
,
设,则,
∵,
∴,
∴,
∴,
则的最小值是.
故选D.
5.D
【分析】由题意可知抛物线开口向上,对称轴是直线x=1,求出(,y3) 直线x=1的对称点,然后根据二次函数的增减性可以判断y1,y2,y3的大小关系,从而可以解答本题.
解:∵y=2(x-1)2+c,2>0,
∴抛物线开口向上,对称轴是直线x=1,
∴当x<1时,y随x的增大而减小;(,y3)关于直线x=1的对称点是(,y3),
∵-2<<0<1
∴y1>y3>y2,
故选D.
6.A
【分析】先求出抛物线的解析式,再列出不等式,求出其解集或,从而可得当x=1时,,有成立,最后求出a的取值范围.
解:∵抛物线P:,将抛物线P绕原点旋转180°得到抛物线,
∴抛物线P与抛物线关于原点对称,
设点(x,y)在抛物线P’上,则点(-x,-y)一定在抛物线P上,
∴
∴抛物线的解析式为,
∵当时,在抛物线上任取一点M,设点M的纵坐标为t,若,
即
令,
∴,
解得:或,
设,
∵开口向下,且与x轴的两个交点为(0,0),(4a,0),
即当时,要恒成立,此时,
∴当x=1时,即可,
得:,
解得:,
又∵
∴
故选A
7.A
【分析】由二次函数解析式,可求与x轴的两个交点A、B,直线表示的图像可看做是直线的图像平移b个单位长度得到,再结合所给函数图像可知,当平移直线经过B点时,恰与所给图像有三个交点,故将B点坐标代入即可求解;当平移直线经过C点时,恰与所给图像有三个交点,即直线与函数关于x轴对称的函数图像只有一个交点,即联立解析式得到的方程的判别式等于0,即可求解.
解:由知,当时,即
解得:
作函数的图像并平移至过点B时,恰与所给图像有三个交点,此时有:
平移图像至过点C时,恰与所给图像有三个交点,即当时,只有一个交点
当的函数图像由的图像关于x轴对称得到
当时对应的解析式为
即,整理得:
综上所述或
故答案是:A.
8.A
【分析】通过解方程x2 2x 3=0得到A、B的坐标,利用二次函数的性质得到顶点的坐标,可写出图象y=(x 1)2 4( 1
y=x2 2x 3=(x 1)2 4,则顶点坐标为(1, 4),
把图象y=(x 1)2 4( 1
当直线y=x+b与y= x2+2x+3( 1
,
舍去;
当直线y=x+b过A( 1,0)时, 1+b=0,解得b=1,
当直线y=x+b过B(3,0)时,3+b=0,解得b= 3,
所以,当 3
9.A
【分析】分点P在AB和BC上两种情况,分别求出MN和PF长,利用面积公式求解.
解:(1)如图,当0≤x≤4时,点P在AB上,过点N作NE⊥AD于点E,设MN与PD交于点F,
∴NE=DC=AD,
则PD= ,
又∵MN垂直平分PD,
∴PF= ,
∴∠MDF+∠FMD=∠MNE+∠FME=90°,
∴∠MNE=∠PDA,
在△MNE和△PDA中,
∴△APD≌△EMN,
∴PD=MN= ,
∴y= ,
(2)如图,当4<x≤8时,点P在BC上,
过点N作NE⊥CD于点E,设MN交PD于点F,
则PD= ,
∴PF
用(1)的方法得
MN,
y=,
故
故选择A.
10.A
【分析】根据二次函数图象与性质,逐项判断即可.
解:∵抛物线开口向下,
∴a<0,
∵对称轴是直线x=1,
∴﹣=1,即b=﹣2a,
∴b>0,
∵抛物线与y轴交点在正半轴,
∴c>0,
∴abc<0,故①正确;
由图象可知,x=3时y<0,
∴9a+3b+c<0,
∴3a+b<﹣c,故②错误;
∵9a+3b+c<0,b=﹣2a,
∴﹣b+3b+c<0,
∴2c<3b,故③正确,
∵x=1时,y=a+b+c是函数的最大值,
∴a(k+1)2+b(k+1)+c≤a+b+c,
∴a(k+1)2+b(k+1)≤a+b,
∴(k+1)(ak+a+b)≤a+b,
故④正确,
∴正确的有①③④,
故选:A.
二、填空题
11. / 0或5/5或0
【分析】(1)先求出抛物线的对称轴为直线,根据点M到y轴的距离不大于1,得出,根据二次函数的增减性,求出b的取值范围即可;
(2)根据点到直线的距离不大于,得出,即,从而得出,然后根据,求出a的范围,即可得出.
解:(1)∵,
∴抛物线的对称轴为直线,
∵点M到y轴的距离不大于1,
∴,
∴此时点M在对称轴的左侧,
∵,
∴在对称轴的左侧随x的增大而减小,
∴当时,b取最大值,且最大值为,
当时,b取最小值,且最小值为,
∴b的取值范围是;
故答案为:;
(2)∵点到直线的距离不大于,
∴,即,
∴,
令,代入,即,解得:,,
令,代入,即,解得:,,
∴点M应为或上的动点,
当时,,
当时,,
综上分析可知,的值为0或5;
故答案为:0或5.
12.
【分析】根据二次函数的性质,可以得到该函数的对称轴,然后再根据当时,函数有最大值,即可得到关于的方程,然后求解即可.
解:∵二次函数,
∴该函数图像对称轴是直线,
当时,当时,该函数取到最大值,
∵当时,函数有最大值,
∴,
解得:(不合题意,舍去);
当时,当时,该函数取到最小值,
当时,
当时,,
当时,,
根据二次函数对称的性质可知:当时,函数有最大值,
又∵当时,函数有最大值,
∴,
解得.
故答案为:.
13.或或
【分析】分两种情况:∠BAC=90°,则由题意得OA=OB,从而得到关于m的方程,解方程即可;∠ACB=90°,则点A、C的纵坐标相同,可得关于m的方程,解方程即可.
解:由题意得:A(m,h),且,
上式中令x=0,得,
∴.
∵点A在直线上,
∴,
即,,
∵点B、点C关于x轴的对称,
则.
①当∠BAC=90°,则OA是Rt△ABC的斜边BC上的中线,
∴OA=OB,
∵,,
则,
由于m≠0,
解得:或,
所以点A的坐标为或;
②当∠ACB=90°时,如图,则AC⊥BC,此时点A、C的纵坐标相同,
即,
∴,m=0(舍去),
所以点A的坐标为;
综上所述,点A的坐标为或或.
14.
【分析】过点B作BD⊥AC于D.根据二次函数的解析式和对称性求出OA和AC的长度,再根据等腰三角形的性质和等角对等边求出BD的长度,最后通过数形结合思想确定OA
∵二次函数的解析式为,
∴当x=0时,y=-4a,二次函数的对称轴是直线.
∴.
∴OA=4a.
∵点在二次函数的图象上,且轴,
∴点A与点C关于直线x=1对称.
∴.
∴AC=2.
∵△ABC是等腰直角三角形,AC为斜边,BD⊥AC,
∴∠BAD=45°,∠BDA=90°,AD=CD=.
∴∠ABD=45°.
∴∠BAD=∠ABD.
∴BD=AD=1.
∵等腰直角三角形的边与轴有两个公共点,
∴OA
∴.
∵a>0,
∴.
故答案为:.
15.,
【分析】根据抛物线y=a(x+m)2+b与x轴的两交点为(-2,0),(1,0),得出方程a(x+m)2+b=0的解,然后根据方程a(x+m)2+b=0的解与a(x+m+2)2+b=0的解的关系得出答案即可.
解:∵抛物线y=a(x+m)2+b与x轴的两交点为(-2,0),(1,0),
∴方程a(x+m)2+b=0的解为x1=-2,x2=1,
∴方程a(x+m+2)2+b=0中,x+2=-2或x+2=1,
∴方程a(x+m+2)2+b=0的解为x1=-4,x2=-1.
故答案为:x1=-4,x2=-1.
16.1或
【分析】先运用根的判别式求得k的取值范围,进而确定k的值,得到抛物线的解析式,再根据折叠得到新图像的解析式,可求出函数图象与x轴的交点坐标,画出函数图象,可发现,若直线与新函数有3个交点,可以有两种情况:①过交点(-1,0),根据待定系数法可得m的值;②不过点(一1,0),与相切时,根据判别式解答即可.
解:∵函数与x轴有两个交点,
∴,解得,
当k取最小整数时,,
∴抛物线为,
将该二次函数图象在x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分不变,得到一个新图象,所以新图象的解析式为(或) :
①因为为的,所以它的图象从左到右是上升的,当它与新图象有3个交点时它一定过,把代入得所以,
②与相切时,图象有三个交点,
,,解得.
故答案为:1或.
17.10
【分析】根据铅球落地时,高度,把实际问题可理解为当时,求x的值即可.
解:当时,,
解得,(舍去),.
故答案为10.
18.
【分析】先根据图形可知AE+CD=AB+AC=2,进而求得AB=AC=1、BC=以及图象最低点的函数值即为AE+CD的最小值;再运用勾股定理求得CD、AE,然后根据AE+CD得到+可知其表示点(x,0)到(0,-1)与(,)的距离之和,然后得当三点共线时有函数值.最后求出该直线的解析式,进而求得x的值.
解:由图可知,当x=0时,AE+CD=AB+AC=2
∴AB=AC=1,BC=,图象最低点函数值即为AE+CD的最小值
由题意可得:CD=,AE=
∴AE+CD=+,即点(x,0)到(0,-1)与(,)的距离之和
∴当这三点共线时,AE+CD最小
设该直线的解析式为y=kx+b
解得
∴
当y=0时,x=.
故填.
三、解答题
19.
(1)解:∵抛物线与x轴交于点,点,
∴,
∴,
∴抛物线解析式为;
(2)解:∵抛物线解析式为,与y轴交于点C,
∴抛物线对称轴为直线,点C的坐标为(0,-3)
如图所示,作点C关于直线的对称点E,连接AE,EQ,则点E的坐标为(2,-3),
由轴对称的性质可知CQ=EQ,
∴△ACQ的周长=AC+AQ+CQ,
要使△ACQ的周长最小,则AQ+CQ最小,即AQ+QE最小,
∴当A、Q、E三点共线时,AQ+QE最小,
设直线AE的解析式为,
∴,
∴,
∴直线AE的解析式为,
当时,,
∴点Q的坐标为(1,-2);
(3)解: 如图1所示,当点P在x轴上方,∠BPM=90°时,过点P作轴,过点M作MF⊥EF于F,过点B作BE⊥EF于E,
∵△PBM是以PB为腰的等腰直角三角形,
∴PA=PB,∠MFP=∠PEB=∠BPM=90°,
∴∠FMP+∠FPM=∠FPM+∠EPB=90°,
∴∠FMP=∠EPB,
∴△FMP≌△EPB(AAS),
∴PE=MF,BE=PF,
设点P的坐标为(1,m),
∴,
∴,,
∴点M的坐标为(1-m,m-2),
∵点M在抛物线上,
∴,
∴,
∴,
解得或(舍去),
∴点M的坐标为(-1,0);
同理当当点P在x轴下方,∠BPM=90°时可以求得点M的坐标为(-1,0);
如图2所示,当点P在x轴上方,∠PBM=90°时,过点B作轴,过点P作PE⊥EF于E,过点M作MF⊥EF于F,设点P的坐标为(1,m),
同理可证△PEB≌△BFM(AAS),
∴,
∴点M的坐标为(3-m,-2),
∵点M在抛物线上,
∴,
∴,
∴,
解得或(舍去),
∴点M的坐标为(,-2);
如图3所示,当点P在x轴下方,∠PBM=90°时,
同理可以求得点M的坐标为(,2);
综上所述,当△PMB是以PB为腰的等腰直角三角形时,点M的坐标为(-1,0)或(,-2)或(,2).
20.
(1)解:二次函数的图象经过点,
.
又抛物线经过点,对称轴为直线,
解得∶
抛物线的表达式为.
(2)解∶①设直线的表达式为.
点A,B的坐标为,,
∴, 解得: ,
直线的表达式为.
根据题意得:点C与点关于对称轴直线对称,
.
设点N的坐标为.
轴,
.
∴
.
,
解,得.
点M的坐标;
②连接与交与点E.
设点M的坐标为,则点N的坐标为
四边形是正方形,
,,.
∵MN⊥x轴,
轴.
E的坐标为.
.
.
∴P的坐标.
点P在抛物线上,
.
解,得,.
点P在第四象限,
舍去.
即.
点M坐标为.
21.
(1)解:设此抛物线的函数解析式为:,
将,,三点代入函数解析式得:
,
解得,
所以此函数解析式为:;
(2)解:连接 ,
∵M点的横坐标为m,且点M在这条抛物线上,
∴M点的坐标为,
∴
,
∵,
当时,S有最大值为:.
(3)解:设,
根据平行四边形的性质知,且,则,为平行四边形的边,
∴Q的横坐标等于P的横坐标,
又∵直线的解析式为,
则,
由,得,
整理得:
所以或
解得或或(不符合题意,舍去),
∵,
∴不可能是对角线
∴由此可得:或或.
22.
详解:(1)依题意得:,解得:,
∴抛物线的解析式为.
∵对称轴为,且抛物线经过,
∴把、分别代入直线,
得,解之得:,
∴直线的解析式为.
(2)直线与对称轴的交点为,则此时的值最小,把代入直线得,
∴.即当点到点的距离与到点的距离之和最小时的坐标为.
(注:本题只求坐标没说要求证明为何此时的值最小,所以答案未证明的值最小的原因).
(3)设,又,,
∴,,,
①若点为直角顶点,则,即:解得:,
②若点为直角顶点,则,即:解得:,
③若点为直角顶点,则,即:解得:
,.
综上所述的坐标为或或或.
23.解:(1)由图像可知,当甲种花卉种植面积m2时,费用y保持不变,为30(元/m2),
所以此区间的函数关系式为:,
当甲种花卉种植面积m2时,函数图像为直线,
设函数关系式为:,
∵当x=40时,y=30,当x=100时,y=15,代入函数关系式得:
,
解得:,
∴
∴当时,y与x的函数关系式应为:
;
(2)∵甲种花卉种植面积不少于30m2,
∵乙种花卉种植面积不低于甲种花卉种植面积的3倍,
,
即,
①当时,
由(1)知,,
∵乙种花卉种植费用为15元/m2.
,
∴当x=90时,,
,
∴种植甲种花卉90m2,乙种花卉270m2时,种植的总费用最少,最少为5625元;
②当时,
由①知,,
∵种植总费用不超过6000元,,
,
即满足条件的x的范围为,
当时,
由①知,,
∵种植总费用不超过6000元,
,
(不符合题意,舍去)或,
即满足条件的x的范围为
综上,满足条件的x的范围为或.
24.解:(1)将两点分别代入,得
解得.
所以抛物线的解析式是.
(2)①如图2,抛物线的对称轴是y轴,当点A与点重合时,,
作于H.
∵是等腰直角三角形,
∴和也是等腰直角三角形,
∴,
∴点C到抛物线的对称轴的距离等于1.
②如图3,设直线PQ的解析式为y=kx+b,由,得
解得
∴直线的解析式为,
设,
∴,
所以.
所以.
将点代入,
得.
整理,得.
因式分解,得.
解得,或(与点P重合,舍去).
当时,.
所以点C的坐标是.
