沪科版九年级数学上册试题 第二十二章 相似形 章节检测卷(含答案)
文档属性
| 名称 | 沪科版九年级数学上册试题 第二十二章 相似形 章节检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-04 20:19:30 | ||
图片预览




文档简介
第二十二章《相似形》章节检测卷
一、单选题(本大题共10小题,每小题3分,共30分)
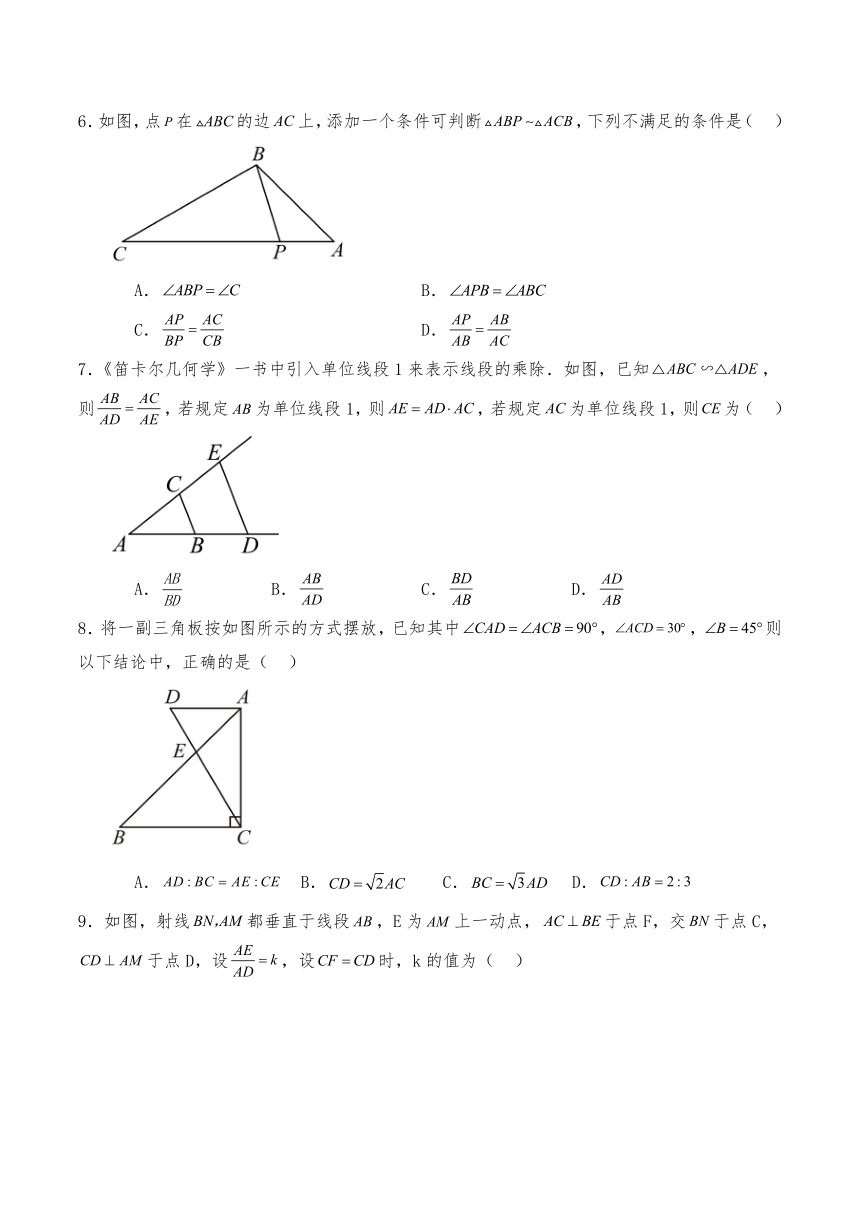
1.若点C是线段AB的黄金分割点,AB=8cm,AC>BC,则AC等于( )
A.cm B.2(﹣1)cm C.4(﹣1)cm D.6(﹣1)cm
2.如果两个相似三角形对应边之比是,那么它们的对应周长之比是( )
A. B. C. D.
3.如图,在中,下列给出的条件,其中不一定能判定的是( )
A. B.
C. D.
4.如图,在中,,且,若,则的长为( )
A. B. C. D.
5.如图,的顶点均在正方形网格的格点上,下列阴影部分的三角形与相似的是( )
A. B.
C. D.
6.如图,点在的边上,添加一个条件可判断,下列不满足的条件是( )
A. B.
C. D.
7.《笛卡尔几何学》一书中引入单位线段1来表示线段的乘除.如图,已知,则,若规定为单位线段1,则,若规定为单位线段1,则为( )
A. B. C. D.
8.将一副三角板按如图所示的方式摆放,已知其中,,则以下结论中,正确的是( )
A. B. C. D.
9.如图,射线都垂直于线段,E为上一动点,于点F,交于点C,于点D,设,设时,k的值为( )
A.1 B. C. D.不存在
10.如图,正方形与正方形边长相等,且三点共线,以为顶点构造菱形,且三点共线,设两块阴影部分的面积分别为和,则的值为( )
A. B. C. D.
二、填空题(本大题共8小题,每小题4分,共32分)
11.已知,则的值等于 .
12.如图,菱形的对角线相交于点O,交于E,若,则菱形的周长 .
13.如图Rt(ABC中,AC⊥BC,CD⊥AB于D,AD=4,BD=2,则CD= .
14.如图,在中,,,按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交于点M、N;②分别以点M、N为圆心,以大于的长为半径作弧,两弧在内交于点O;③作射线,交于点D.若,则的长为 .
15.如图,矩形中,,,剪去一个矩形后,余下的矩形矩形,则的长为 .
16.四边形和四边形是位似图形,点A与点对应,点B与点对应,点O是位似中心,如果,那么 .
17.如图,在正方形中,G为边上一点,将沿翻折到处,延长交边于点E,过点F作分别交,,于点H,P,Q,请完成下列问题:
(1) .
(2)若,则 .
18.2002年的国际数学家大会在中国北京举行,这是21世纪全世界数学家的第一次大聚会.这次大会的会徽选定了我国古代数学家赵爽用来证明勾股定理的弦图,世人称之为“赵爽弦图”.如图,用四个全等的直角三角形()拼成“赵爽弦图”,得到正方形与正方形,连接和,与、、分别相交于点P、O、Q,若,则的值是 .
三、解答题(本大题共6小题,共58分)
19.(8分)如图,,已知,.
(1)若,求的长;
(2)若,求的长.
20.(8分)已知:如图,点D在三角形ABC的AB上,DE交AC于点E,,点F在AD上,且.求证:
(1);
(2)∽.
21.(10分)在①,②,③这三个条件中选择其中一个,补充在下面的问题中,使命题正确,并证明.
问题:如图,四边形的两条对角线交于点,若 (填序号)
求证:.
22.(10分)如图,在中,已知A,且,将与重合在一起,不动,运动,并满足:点在边上沿到的方向运动,且始终经过点与交于点.
(1)求证:;
(2)当点运动到边的中点时,求的长;
(3)探究:在运动过程中,重叠部分能否构成等腰三角形,若能,求出的长;若不能,请说明理由.
23.(10分)在正方形中,点E、F分别是边上的点,连接且.
(1)如图1,当点G在上时,求证:;
(2)如图2,当点B与点E重合时,分别交于点M,N,求证:.
24.(12分)如图,为正方形对角线上的一点,连接并延长交于点,过作分别交,于,.
(1)如图1,求证:;
(2)如图2,点与点关于直线对称,连接并延长交直线于点,连接.
①设的度数为,求的度数:
②猜想与之间的数量关系,并证明.
答案
一、单选题
1.C
【分析】把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值叫做黄金比.
解:根据黄金分割点的概念得:.
故选:C.
2.B
【分析】根据相似三角形对应边的比叫相似比,周长的比等于相似比解答即可.
解:两个相似三角形对应边之比是,
两个相似三角形的相似比为,
它们的周长比为.
故选:B.
3.C
【分析】根据平行线是判定,比例线段的性质,相似三角形的判定和性质,即可.
解:∵
∴
∴A正确,不符合题意;
∵
∴
∴
∴
∴且是公共角
∴
∴
∴
∴B、D正确,不符合题意;
∵是公共角,但不是与,与的夹角
∴与不一定相似
∴不能确定、、、之间的关系
∴与不一定平行
∴C不能判定,符合题意.
故选:C.
4.B
【分析】根据,且,可根据平行线分线段成比例分别求出的长,由此即可求解.
解:∵,,
∴,则,
∵,
∴,则,
∵,
∴,则,
∵,
∴,
∴,
∴,
∴,
故选:.
5.A
【分析】应用两三角形相似判定定理,三边对应成比例,分别对各选项进行分析即可得出答案.
解:在中,
,,,
A、三边分别为,,,则,故与相似,符合题意;
B、三边分别为,,,则,故与不相似,不符合题意;
C、三边分别为,,,则,故与不相似,不符合题意;
D、三边分别为,,,则,故与不相似,不符合题意;
故选:A.
6.C
【分析】根据相似三角形的判定方法,逐项判断即可.
解:∵在和中,,
∴当时,满足两组角对应相等,可判断,故A不符合题意.
当时,满足两组角对应相等,可判断,故B不符合题意.
当时,其夹角不相等,则不能判断,故C符合题意.
当时,满足两边对应成比例且夹角相等,可判断,故D不符合题意.
故选:C.
7.C
【分析】由,可得,根据比例的性质可得,即,由于规定为单位线段1,则,即可解答.
解:∵,
∴,
∴,
即,
∴,
∵规定为单位线段1,
∴.
故选:C.
8.C
【分析】由可得,即可判断;设,根据直角三角形的性质和勾股定理分别表示出,,的长,即可判断,,.
解:,
,
,
又,
,
,故错误;
设,则,
,
,,故错误,正确;
,
,故错误.
故选:.
9.C
【分析】由于,易得,因此只需求得即可.可设;再证明得到,联立,即可求得的比例关系,由此得解.
解:设,则
∵射线都垂直于线段,
∴;
∴;
∵,
∴四边形是矩形,
∴,
∵,
∴,
∴,
∴;
∴,
整理得,
解得,
∴
∴,
故选:C.
10.B
【分析】根据正方形的性质及全等三角形的判定和性质得到,再根据相似三角形的判定与性质得到即可解答.
解:如图所示连接作,与于点,
∵正方形ABCD与正方形DEFG边长相等,
∴,
∴在和中,
,
∴,
∴,
∴,
同理可得:,
∴,,
∴,
∴,
∴,,
∴,
∴,
∵,
∴,
∴,,
∴,
∵,
∴,
∴,
∵ ,
∴ ,
∴,
故选.
二、填空题
11.
【分析】根据比的性质,运用特殊值解法,令,,代入求值即可.
解:∵,令,,
∴,
故答案为:.
12.16
【分析】由菱形的性质和三角形中位线定理即可得菱形的边长,从而可求得菱形的周长.
解:∵四边形是菱形,且对角线相交于点O,
∴点O是的中点,
∵,
∴,
∴E为的中点,
∴为的中位线,
∴
∴菱形的周长为:
故答案为:16
13.
【分析】由于AC⊥BC,CD⊥AB,可得一组对应角相等,进而可证得,因此可证得△BCD∽△CAD,列出比例式可求CD.
解:∵AC⊥BC,CD⊥AB,
∴,
∴,
,
∴,
∴△BCD∽△CAD,
∴,
∴,
∵AD=4,BD=2,
∴.
14.
【分析】过D点作DH⊥AB于H点,由题中作法得平分,根据得,根据得,在中,根据勾股定理得,
根据得,则,进行计算即可得.
解:如图,过D点作DH⊥AB于H点,
由题中作法得平分,
∵
∴
∵,
∴,
在中,根据勾股定理得,
∵,
∴,
∴,
即,
∴,
故答案为:.
15.1
【分析】根据相似多边形的性质得,即,然后利用比例性质求出即可.
解:∵四边形是矩形,
∴,
∵四边形是矩形,
∴,
∵余下的矩形矩形,
∴,即,
∴,
故答案为:1.
16.
【分析】由四边形与四边形位似,得四边形与四边形相似,可知,,进而可求出的比值.
解:四边形与四边形位似,
四边形四边形,
∴,
∴,
,
故答案为:.
17.
【分析】(1)根据折叠得出,证明,得出,根据,求出结果即可;
(2)过点H作于点M,证明,得出,,证明,得出,设,则,得出,得出,根据,求出x的值,即可得出答案.
解:(1)∵四边形为正方形,
∴,,
根据折叠可知,,,,
∴,,
∵,
∴,
∴,
∴;
故答案为:;
(2)过点H作于点M,如图所示:
∵,
∴,
∴,
∵,,
∴,
∴,,
∵,,
∴,
∴,
∵,
∴,
设,
∴,
∴,
∴,
∴,
∴,
解得:,
∴.
故答案为:.
18.
【分析】设,,则,证明,利用相似三角形的性质求出,可得,,利用勾股定理求出和,进而可得的长,再证明,可得,然后根据正方形的性质求出,即可得出答案.
解:设,,则,
∵,,
∴,
∴,
∵,
∴,,
∴,
∴,
整理得:,
解得:,(舍去),
即,
∴,,
∴,,
∴,
∴
∴,
∵四边形是正方形,
∴,,
又∵,
∴,
∴,
又∵,
∴,
∴,
故答案为:.
三、解答题
19.
解:(1),
∴
解得:
(2)解:设的长是.,
,
∴
解得:
20.
解:(1)证明:∵,
∴,
∴,
∴.
(2)证明:∵,
∴,
∵,
∴.
又,
∴∽.
21.
解:选择条件①的证明为:
∵,
∴,
又∵,
∴;
选择条件②的证明为:
∵,
∴.
22.
解:(1)证明:∵,
∴,
又∵
又∵,
∴,
∴,
∴;
(2)解:∵点是边的中点,,
∴
∵
∴,即:,
∴;
(3)解:∵,且
∴,
∴,
当时,则,
∴,
∴,
当时,
∴,
∴,
即,
又∵,
∴,
∴,
∴,
∴,
当时,点与点重合,即,此时重叠部分图形不能构成三角形;
综上所述,或.
23.
解:(1)证明:∵四边形是正方形,
∴,
∵,
∴,
∴,
在和中,
,
∴,
∴,
∴,
∴,
∴.
(2)解:如图2,作交的延长线于点H,则,
∵点E与点B重合,且,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴.
24.
解:证明:(1)作,垂足为,
∵四边形ABCD为正方形,
∴∠B=∠NAB=90°,∠NHB=90°,
∴∠B=∠NAB=∠NHB=90°,
∴四边形ABHN为矩形,
∴,
,
,又,
,
,
;
(2)①.
点与点关于直线对称,且四边形是正方形,
,,
,
在等腰中,,
又,
;
②.
证明:连接,,
由对称性可知,
即是等腰直角三角形,
∴FC,
,
∵四边形ABCD为正方形,
∴,
,
,
又,
,
,
.
一、单选题(本大题共10小题,每小题3分,共30分)
1.若点C是线段AB的黄金分割点,AB=8cm,AC>BC,则AC等于( )
A.cm B.2(﹣1)cm C.4(﹣1)cm D.6(﹣1)cm
2.如果两个相似三角形对应边之比是,那么它们的对应周长之比是( )
A. B. C. D.
3.如图,在中,下列给出的条件,其中不一定能判定的是( )
A. B.
C. D.
4.如图,在中,,且,若,则的长为( )
A. B. C. D.
5.如图,的顶点均在正方形网格的格点上,下列阴影部分的三角形与相似的是( )
A. B.
C. D.
6.如图,点在的边上,添加一个条件可判断,下列不满足的条件是( )
A. B.
C. D.
7.《笛卡尔几何学》一书中引入单位线段1来表示线段的乘除.如图,已知,则,若规定为单位线段1,则,若规定为单位线段1,则为( )
A. B. C. D.
8.将一副三角板按如图所示的方式摆放,已知其中,,则以下结论中,正确的是( )
A. B. C. D.
9.如图,射线都垂直于线段,E为上一动点,于点F,交于点C,于点D,设,设时,k的值为( )
A.1 B. C. D.不存在
10.如图,正方形与正方形边长相等,且三点共线,以为顶点构造菱形,且三点共线,设两块阴影部分的面积分别为和,则的值为( )
A. B. C. D.
二、填空题(本大题共8小题,每小题4分,共32分)
11.已知,则的值等于 .
12.如图,菱形的对角线相交于点O,交于E,若,则菱形的周长 .
13.如图Rt(ABC中,AC⊥BC,CD⊥AB于D,AD=4,BD=2,则CD= .
14.如图,在中,,,按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交于点M、N;②分别以点M、N为圆心,以大于的长为半径作弧,两弧在内交于点O;③作射线,交于点D.若,则的长为 .
15.如图,矩形中,,,剪去一个矩形后,余下的矩形矩形,则的长为 .
16.四边形和四边形是位似图形,点A与点对应,点B与点对应,点O是位似中心,如果,那么 .
17.如图,在正方形中,G为边上一点,将沿翻折到处,延长交边于点E,过点F作分别交,,于点H,P,Q,请完成下列问题:
(1) .
(2)若,则 .
18.2002年的国际数学家大会在中国北京举行,这是21世纪全世界数学家的第一次大聚会.这次大会的会徽选定了我国古代数学家赵爽用来证明勾股定理的弦图,世人称之为“赵爽弦图”.如图,用四个全等的直角三角形()拼成“赵爽弦图”,得到正方形与正方形,连接和,与、、分别相交于点P、O、Q,若,则的值是 .
三、解答题(本大题共6小题,共58分)
19.(8分)如图,,已知,.
(1)若,求的长;
(2)若,求的长.
20.(8分)已知:如图,点D在三角形ABC的AB上,DE交AC于点E,,点F在AD上,且.求证:
(1);
(2)∽.
21.(10分)在①,②,③这三个条件中选择其中一个,补充在下面的问题中,使命题正确,并证明.
问题:如图,四边形的两条对角线交于点,若 (填序号)
求证:.
22.(10分)如图,在中,已知A,且,将与重合在一起,不动,运动,并满足:点在边上沿到的方向运动,且始终经过点与交于点.
(1)求证:;
(2)当点运动到边的中点时,求的长;
(3)探究:在运动过程中,重叠部分能否构成等腰三角形,若能,求出的长;若不能,请说明理由.
23.(10分)在正方形中,点E、F分别是边上的点,连接且.
(1)如图1,当点G在上时,求证:;
(2)如图2,当点B与点E重合时,分别交于点M,N,求证:.
24.(12分)如图,为正方形对角线上的一点,连接并延长交于点,过作分别交,于,.
(1)如图1,求证:;
(2)如图2,点与点关于直线对称,连接并延长交直线于点,连接.
①设的度数为,求的度数:
②猜想与之间的数量关系,并证明.
答案
一、单选题
1.C
【分析】把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值叫做黄金比.
解:根据黄金分割点的概念得:.
故选:C.
2.B
【分析】根据相似三角形对应边的比叫相似比,周长的比等于相似比解答即可.
解:两个相似三角形对应边之比是,
两个相似三角形的相似比为,
它们的周长比为.
故选:B.
3.C
【分析】根据平行线是判定,比例线段的性质,相似三角形的判定和性质,即可.
解:∵
∴
∴A正确,不符合题意;
∵
∴
∴
∴
∴且是公共角
∴
∴
∴
∴B、D正确,不符合题意;
∵是公共角,但不是与,与的夹角
∴与不一定相似
∴不能确定、、、之间的关系
∴与不一定平行
∴C不能判定,符合题意.
故选:C.
4.B
【分析】根据,且,可根据平行线分线段成比例分别求出的长,由此即可求解.
解:∵,,
∴,则,
∵,
∴,则,
∵,
∴,则,
∵,
∴,
∴,
∴,
∴,
故选:.
5.A
【分析】应用两三角形相似判定定理,三边对应成比例,分别对各选项进行分析即可得出答案.
解:在中,
,,,
A、三边分别为,,,则,故与相似,符合题意;
B、三边分别为,,,则,故与不相似,不符合题意;
C、三边分别为,,,则,故与不相似,不符合题意;
D、三边分别为,,,则,故与不相似,不符合题意;
故选:A.
6.C
【分析】根据相似三角形的判定方法,逐项判断即可.
解:∵在和中,,
∴当时,满足两组角对应相等,可判断,故A不符合题意.
当时,满足两组角对应相等,可判断,故B不符合题意.
当时,其夹角不相等,则不能判断,故C符合题意.
当时,满足两边对应成比例且夹角相等,可判断,故D不符合题意.
故选:C.
7.C
【分析】由,可得,根据比例的性质可得,即,由于规定为单位线段1,则,即可解答.
解:∵,
∴,
∴,
即,
∴,
∵规定为单位线段1,
∴.
故选:C.
8.C
【分析】由可得,即可判断;设,根据直角三角形的性质和勾股定理分别表示出,,的长,即可判断,,.
解:,
,
,
又,
,
,故错误;
设,则,
,
,,故错误,正确;
,
,故错误.
故选:.
9.C
【分析】由于,易得,因此只需求得即可.可设;再证明得到,联立,即可求得的比例关系,由此得解.
解:设,则
∵射线都垂直于线段,
∴;
∴;
∵,
∴四边形是矩形,
∴,
∵,
∴,
∴,
∴;
∴,
整理得,
解得,
∴
∴,
故选:C.
10.B
【分析】根据正方形的性质及全等三角形的判定和性质得到,再根据相似三角形的判定与性质得到即可解答.
解:如图所示连接作,与于点,
∵正方形ABCD与正方形DEFG边长相等,
∴,
∴在和中,
,
∴,
∴,
∴,
同理可得:,
∴,,
∴,
∴,
∴,,
∴,
∴,
∵,
∴,
∴,,
∴,
∵,
∴,
∴,
∵ ,
∴ ,
∴,
故选.
二、填空题
11.
【分析】根据比的性质,运用特殊值解法,令,,代入求值即可.
解:∵,令,,
∴,
故答案为:.
12.16
【分析】由菱形的性质和三角形中位线定理即可得菱形的边长,从而可求得菱形的周长.
解:∵四边形是菱形,且对角线相交于点O,
∴点O是的中点,
∵,
∴,
∴E为的中点,
∴为的中位线,
∴
∴菱形的周长为:
故答案为:16
13.
【分析】由于AC⊥BC,CD⊥AB,可得一组对应角相等,进而可证得,因此可证得△BCD∽△CAD,列出比例式可求CD.
解:∵AC⊥BC,CD⊥AB,
∴,
∴,
,
∴,
∴△BCD∽△CAD,
∴,
∴,
∵AD=4,BD=2,
∴.
14.
【分析】过D点作DH⊥AB于H点,由题中作法得平分,根据得,根据得,在中,根据勾股定理得,
根据得,则,进行计算即可得.
解:如图,过D点作DH⊥AB于H点,
由题中作法得平分,
∵
∴
∵,
∴,
在中,根据勾股定理得,
∵,
∴,
∴,
即,
∴,
故答案为:.
15.1
【分析】根据相似多边形的性质得,即,然后利用比例性质求出即可.
解:∵四边形是矩形,
∴,
∵四边形是矩形,
∴,
∵余下的矩形矩形,
∴,即,
∴,
故答案为:1.
16.
【分析】由四边形与四边形位似,得四边形与四边形相似,可知,,进而可求出的比值.
解:四边形与四边形位似,
四边形四边形,
∴,
∴,
,
故答案为:.
17.
【分析】(1)根据折叠得出,证明,得出,根据,求出结果即可;
(2)过点H作于点M,证明,得出,,证明,得出,设,则,得出,得出,根据,求出x的值,即可得出答案.
解:(1)∵四边形为正方形,
∴,,
根据折叠可知,,,,
∴,,
∵,
∴,
∴,
∴;
故答案为:;
(2)过点H作于点M,如图所示:
∵,
∴,
∴,
∵,,
∴,
∴,,
∵,,
∴,
∴,
∵,
∴,
设,
∴,
∴,
∴,
∴,
∴,
解得:,
∴.
故答案为:.
18.
【分析】设,,则,证明,利用相似三角形的性质求出,可得,,利用勾股定理求出和,进而可得的长,再证明,可得,然后根据正方形的性质求出,即可得出答案.
解:设,,则,
∵,,
∴,
∴,
∵,
∴,,
∴,
∴,
整理得:,
解得:,(舍去),
即,
∴,,
∴,,
∴,
∴
∴,
∵四边形是正方形,
∴,,
又∵,
∴,
∴,
又∵,
∴,
∴,
故答案为:.
三、解答题
19.
解:(1),
∴
解得:
(2)解:设的长是.,
,
∴
解得:
20.
解:(1)证明:∵,
∴,
∴,
∴.
(2)证明:∵,
∴,
∵,
∴.
又,
∴∽.
21.
解:选择条件①的证明为:
∵,
∴,
又∵,
∴;
选择条件②的证明为:
∵,
∴.
22.
解:(1)证明:∵,
∴,
又∵
又∵,
∴,
∴,
∴;
(2)解:∵点是边的中点,,
∴
∵
∴,即:,
∴;
(3)解:∵,且
∴,
∴,
当时,则,
∴,
∴,
当时,
∴,
∴,
即,
又∵,
∴,
∴,
∴,
∴,
当时,点与点重合,即,此时重叠部分图形不能构成三角形;
综上所述,或.
23.
解:(1)证明:∵四边形是正方形,
∴,
∵,
∴,
∴,
在和中,
,
∴,
∴,
∴,
∴,
∴.
(2)解:如图2,作交的延长线于点H,则,
∵点E与点B重合,且,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴.
24.
解:证明:(1)作,垂足为,
∵四边形ABCD为正方形,
∴∠B=∠NAB=90°,∠NHB=90°,
∴∠B=∠NAB=∠NHB=90°,
∴四边形ABHN为矩形,
∴,
,
,又,
,
,
;
(2)①.
点与点关于直线对称,且四边形是正方形,
,,
,
在等腰中,,
又,
;
②.
证明:连接,,
由对称性可知,
即是等腰直角三角形,
∴FC,
,
∵四边形ABCD为正方形,
∴,
,
,
又,
,
,
.
