人教版数学九年级下册 第二十六章 反比例函数测试卷(含答案)
文档属性
| 名称 | 人教版数学九年级下册 第二十六章 反比例函数测试卷(含答案) | 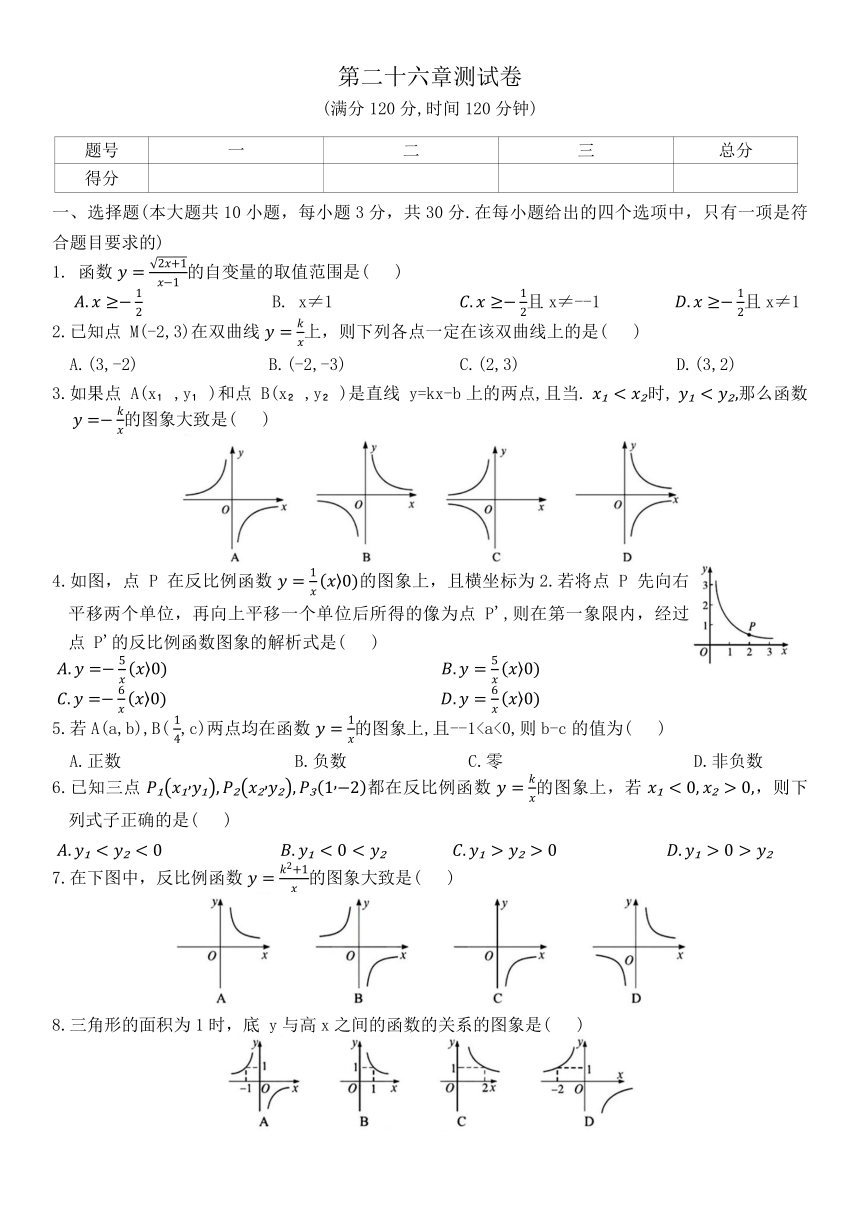 | |
| 格式 | docx | ||
| 文件大小 | 573.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-05 07:38:08 | ||
图片预览


文档简介
第二十六章测试卷
(满分120分,时间120分钟)
题号 一 二 三 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 函数 的自变量的取值范围是( )
B. x≠1 且x≠--1 且x≠1
2.已知点 M(-2,3)在双曲线 上,则下列各点一定在该双曲线上的是( )
A.(3,-2) B.(-2,-3) C.(2,3) D.(3,2)
3.如果点 A(x ,y )和点 B(x ,y )是直线 y=kx-b上的两点,且当. 时, 那么函数 的图象大致是( )
4.如图,点 P 在反比例函数 的图象上,且横坐标为2.若将点 P 先向右平移两个单位,再向上平移一个单位后所得的像为点 P',则在第一象限内,经过点 P'的反比例函数图象的解析式是( )
5.若A(a,b),B( ,c)两点均在函数 的图象上,且--1A.正数 B.负数 C.零 D.非负数
6.已知三点 都在反比例函数 的图象上,若 ,则下列式子正确的是( )
7.在下图中,反比例函数 的图象大致是( )
8.三角形的面积为1时,底 y与高x之间的函数的关系的图象是( )
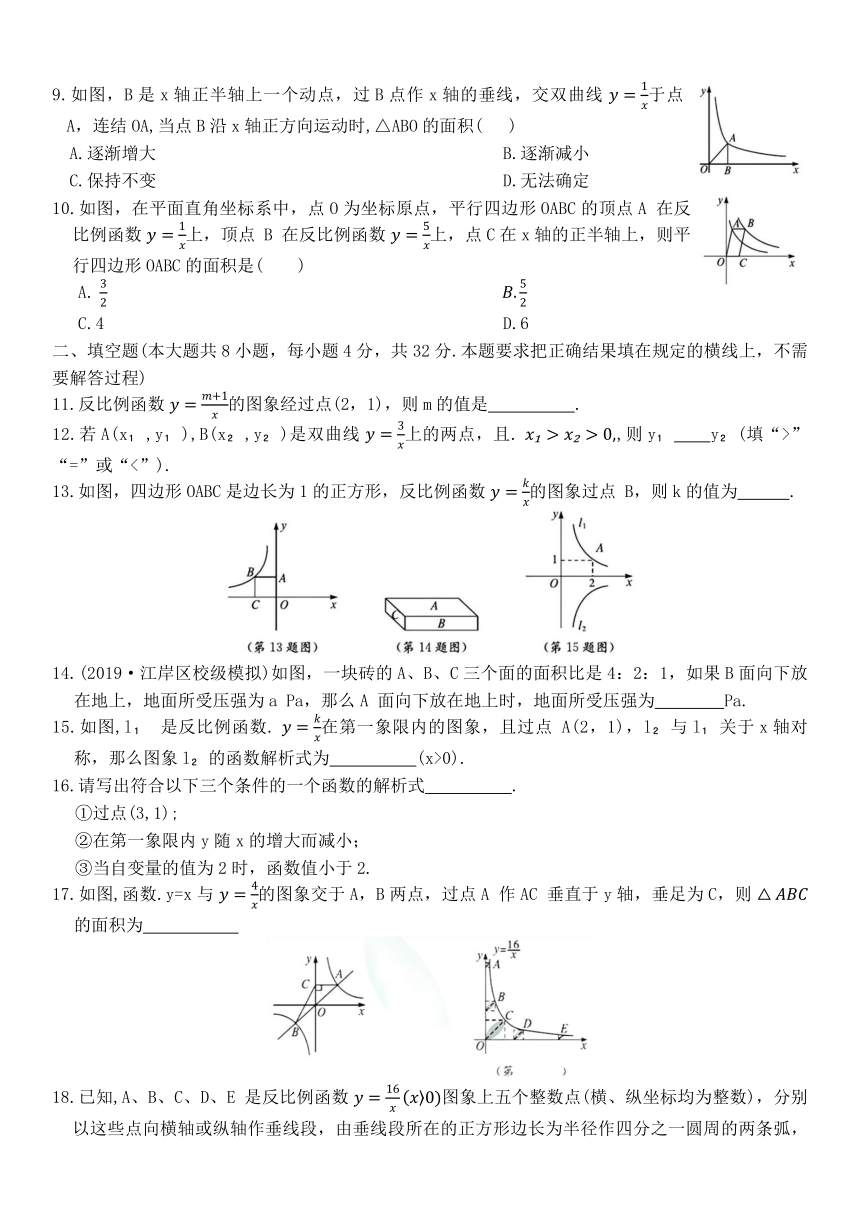
9.如图,B是x轴正半轴上一个动点,过B点作x轴的垂线,交双曲线 于点A,连结OA,当点B沿x轴正方向运动时,△ABO的面积( )
A.逐渐增大 B.逐渐减小
C.保持不变 D.无法确定
10.如图,在平面直角坐标系中,点O为坐标原点,平行四边形OABC的顶点A 在反比例函数 上,顶点 B 在反比例函数 上,点C在x轴的正半轴上,则平行四边形OABC的面积是( )
A.
C.4 D.6
二、填空题(本大题共8小题,每小题4分,共32分.本题要求把正确结果填在规定的横线上,不需要解答过程)
11.反比例函数 的图象经过点(2,1),则m的值是 .
12.若A(x ,y ),B(x ,y )是双曲线 上的两点,且. ,则y y (填“>”“=”或“<”).
13.如图,四边形OABC是边长为1的正方形,反比例函数 的图象过点 B,则k的值为 .
14.(2019·江岸区校级模拟)如图,一块砖的A、B、C三个面的面积比是4:2:1,如果B面向下放在地上,地面所受压强为a Pa,那么A 面向下放在地上时,地面所受压强为 Pa.
15.如图,l 是反比例函数. 在第一象限内的图象,且过点 A(2,1),l 与l 关于x轴对称,那么图象l 的函数解析式为 (x>0).
16.请写出符合以下三个条件的一个函数的解析式 .
①过点(3,1);
②在第一象限内y随x的增大而减小;
③当自变量的值为2时,函数值小于2.
17.如图,函数.y=x与 的图象交于A,B两点,过点A 作AC 垂直于y轴,垂足为C,则 的面积为
18.已知,A、B、C、D、E 是反比例函数 图象上五个整数点(横、纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是 (用含π的代数式表示).
三、解答题(本大题共6小题,满分58分.解答应写出文字说明、证明过程或演算步骤)
19.(8分)已知正比例函数. 与反比例函数 的图象交于A、B 两点,点 A 的坐标为(2,1).
(1)求正比例函数、反比例函数的表达式;
(2)求点 B 的坐标.
20.(8分)如图,反比例函数 的图象与一次函数. 的图象交于点A(m,2),点B(-2,n),一次函数图象与y轴的交点为C.
(1)求一次函数解析式;
(2)求C点的坐标;
(3)求 的面积.
21.(10分)如图,直线. 与反比例函数 的图象相交于点 A、点B,与x轴交于点C,其中点 A 的坐标为( 点 B 的横坐标为
(1)试确定反比例函数的关系式;
(2)求 的面积.
22.(10分)如图所示,一次函数 的图象与反比例函数 的图象交于M,N两点.
(1)求反比例函数与一次函数的解析式;
(2)根据图象写出使反比例函数的值大于一次函数的值的x的范围.
23.(10分)如图,D 是反比例函数 的图象上一点,过D作. 轴于E, y轴于C,一次函数 与 的图象都经过点C,与x轴分别交于A、B两点,四边形DCAE的面积为4,求k的值.
24.(12分)已知一次函数. )和反比例函数 的图象交于点A(1,1).
(1)求两个函数的解析式;
(2)若点 B是x 轴上一点,且 是直角三角形,求 B 点的坐标.
第二十六章测试卷
1. D 2. A 3. B 4. D 5. B 6. D 7. D 8. C 9. C10. C
11.1 12.< 13.-1 14. a/2
16.不唯一,如
17.4
18.13π-26
19.解:(1)把点 A(2,1)分别代入 与 得,
∴正比例函数、反比例函数的表达式为:
(2)由方程组 得
∴B点坐标是(-2,-1).
20.解:(1)由题意,把A(m,2),B(-2,n)代入 中,得 ∴A(1,2),B(-2,-1).
将A、B代入y=kx+b中得 ∴一次函数解析式为y=x+1.
(2)C(0,1)
21.解:(1)∵点A(-2,4)在反比例函数图象上,∴k=-2×4=-8.
∴反比例函数解析式为
(2)∵B点的横坐标为-4,∴y=2,∴B(-4,2).
∵点A(-2,4)、点B(-4,2)在直线y=kx+b上,
解得
∴直线AB为y=x+6.
与x轴的交点坐标C(-
22.解:(1)把 N(-1,-4)代入 中,得 所以k=4.
反比例函数的表达式为
又点M(2,m)在双曲线上,所以m=2,即点M(2,2).
把M(2,2),N(--1,--4)代入 y=ax+b中,得 解得
故一次函数的表达式为y=2x-2.
(2)由图象可知,当x<-1或023.解:∵点C在 的图象上,∴点C的坐标为(0,2).
将点C(0,2)代入到y=-x+m中,得m=2.
∴点A的坐标是(2,0).∴△OCA的面积为
∵四边形DCAE的面积为4,
∴矩形OCDE的面积为4-2=2.∴CD=1.
∴点D的坐标是D(--1,2),代入到 中,得k=-2.
24.解:(1)∵点A(1,1)在反比例函数 的图象上,
∴k=2.∴反比例函数的解析式为:
一次函数的解析式为:y=2x+b.
∵点A(1,1)在一次函数y=2x+b的图象上,∴b=--1.
∴一次函数的解析式为y=2x--1.
(2)∵点A(1,1),∴∠AOB=45°.
∵△AOB是直角三角形,∴点B只能在x轴正半轴上.
①当 时,即
②当 时,
∴B 是( 中点,
综上可知,B点坐标为(1,0)或(2,0).
(满分120分,时间120分钟)
题号 一 二 三 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 函数 的自变量的取值范围是( )
B. x≠1 且x≠--1 且x≠1
2.已知点 M(-2,3)在双曲线 上,则下列各点一定在该双曲线上的是( )
A.(3,-2) B.(-2,-3) C.(2,3) D.(3,2)
3.如果点 A(x ,y )和点 B(x ,y )是直线 y=kx-b上的两点,且当. 时, 那么函数 的图象大致是( )
4.如图,点 P 在反比例函数 的图象上,且横坐标为2.若将点 P 先向右平移两个单位,再向上平移一个单位后所得的像为点 P',则在第一象限内,经过点 P'的反比例函数图象的解析式是( )
5.若A(a,b),B( ,c)两点均在函数 的图象上,且--1
6.已知三点 都在反比例函数 的图象上,若 ,则下列式子正确的是( )
7.在下图中,反比例函数 的图象大致是( )
8.三角形的面积为1时,底 y与高x之间的函数的关系的图象是( )
9.如图,B是x轴正半轴上一个动点,过B点作x轴的垂线,交双曲线 于点A,连结OA,当点B沿x轴正方向运动时,△ABO的面积( )
A.逐渐增大 B.逐渐减小
C.保持不变 D.无法确定
10.如图,在平面直角坐标系中,点O为坐标原点,平行四边形OABC的顶点A 在反比例函数 上,顶点 B 在反比例函数 上,点C在x轴的正半轴上,则平行四边形OABC的面积是( )
A.
C.4 D.6
二、填空题(本大题共8小题,每小题4分,共32分.本题要求把正确结果填在规定的横线上,不需要解答过程)
11.反比例函数 的图象经过点(2,1),则m的值是 .
12.若A(x ,y ),B(x ,y )是双曲线 上的两点,且. ,则y y (填“>”“=”或“<”).
13.如图,四边形OABC是边长为1的正方形,反比例函数 的图象过点 B,则k的值为 .
14.(2019·江岸区校级模拟)如图,一块砖的A、B、C三个面的面积比是4:2:1,如果B面向下放在地上,地面所受压强为a Pa,那么A 面向下放在地上时,地面所受压强为 Pa.
15.如图,l 是反比例函数. 在第一象限内的图象,且过点 A(2,1),l 与l 关于x轴对称,那么图象l 的函数解析式为 (x>0).
16.请写出符合以下三个条件的一个函数的解析式 .
①过点(3,1);
②在第一象限内y随x的增大而减小;
③当自变量的值为2时,函数值小于2.
17.如图,函数.y=x与 的图象交于A,B两点,过点A 作AC 垂直于y轴,垂足为C,则 的面积为
18.已知,A、B、C、D、E 是反比例函数 图象上五个整数点(横、纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是 (用含π的代数式表示).
三、解答题(本大题共6小题,满分58分.解答应写出文字说明、证明过程或演算步骤)
19.(8分)已知正比例函数. 与反比例函数 的图象交于A、B 两点,点 A 的坐标为(2,1).
(1)求正比例函数、反比例函数的表达式;
(2)求点 B 的坐标.
20.(8分)如图,反比例函数 的图象与一次函数. 的图象交于点A(m,2),点B(-2,n),一次函数图象与y轴的交点为C.
(1)求一次函数解析式;
(2)求C点的坐标;
(3)求 的面积.
21.(10分)如图,直线. 与反比例函数 的图象相交于点 A、点B,与x轴交于点C,其中点 A 的坐标为( 点 B 的横坐标为
(1)试确定反比例函数的关系式;
(2)求 的面积.
22.(10分)如图所示,一次函数 的图象与反比例函数 的图象交于M,N两点.
(1)求反比例函数与一次函数的解析式;
(2)根据图象写出使反比例函数的值大于一次函数的值的x的范围.
23.(10分)如图,D 是反比例函数 的图象上一点,过D作. 轴于E, y轴于C,一次函数 与 的图象都经过点C,与x轴分别交于A、B两点,四边形DCAE的面积为4,求k的值.
24.(12分)已知一次函数. )和反比例函数 的图象交于点A(1,1).
(1)求两个函数的解析式;
(2)若点 B是x 轴上一点,且 是直角三角形,求 B 点的坐标.
第二十六章测试卷
1. D 2. A 3. B 4. D 5. B 6. D 7. D 8. C 9. C10. C
11.1 12.< 13.-1 14. a/2
16.不唯一,如
17.4
18.13π-26
19.解:(1)把点 A(2,1)分别代入 与 得,
∴正比例函数、反比例函数的表达式为:
(2)由方程组 得
∴B点坐标是(-2,-1).
20.解:(1)由题意,把A(m,2),B(-2,n)代入 中,得 ∴A(1,2),B(-2,-1).
将A、B代入y=kx+b中得 ∴一次函数解析式为y=x+1.
(2)C(0,1)
21.解:(1)∵点A(-2,4)在反比例函数图象上,∴k=-2×4=-8.
∴反比例函数解析式为
(2)∵B点的横坐标为-4,∴y=2,∴B(-4,2).
∵点A(-2,4)、点B(-4,2)在直线y=kx+b上,
解得
∴直线AB为y=x+6.
与x轴的交点坐标C(-
22.解:(1)把 N(-1,-4)代入 中,得 所以k=4.
反比例函数的表达式为
又点M(2,m)在双曲线上,所以m=2,即点M(2,2).
把M(2,2),N(--1,--4)代入 y=ax+b中,得 解得
故一次函数的表达式为y=2x-2.
(2)由图象可知,当x<-1或0
将点C(0,2)代入到y=-x+m中,得m=2.
∴点A的坐标是(2,0).∴△OCA的面积为
∵四边形DCAE的面积为4,
∴矩形OCDE的面积为4-2=2.∴CD=1.
∴点D的坐标是D(--1,2),代入到 中,得k=-2.
24.解:(1)∵点A(1,1)在反比例函数 的图象上,
∴k=2.∴反比例函数的解析式为:
一次函数的解析式为:y=2x+b.
∵点A(1,1)在一次函数y=2x+b的图象上,∴b=--1.
∴一次函数的解析式为y=2x--1.
(2)∵点A(1,1),∴∠AOB=45°.
∵△AOB是直角三角形,∴点B只能在x轴正半轴上.
①当 时,即
②当 时,
∴B 是( 中点,
综上可知,B点坐标为(1,0)或(2,0).
