第二章 直角三角形的边角关系 6 利用三角函数测高
文档属性
| 名称 | 第二章 直角三角形的边角关系 6 利用三角函数测高 | 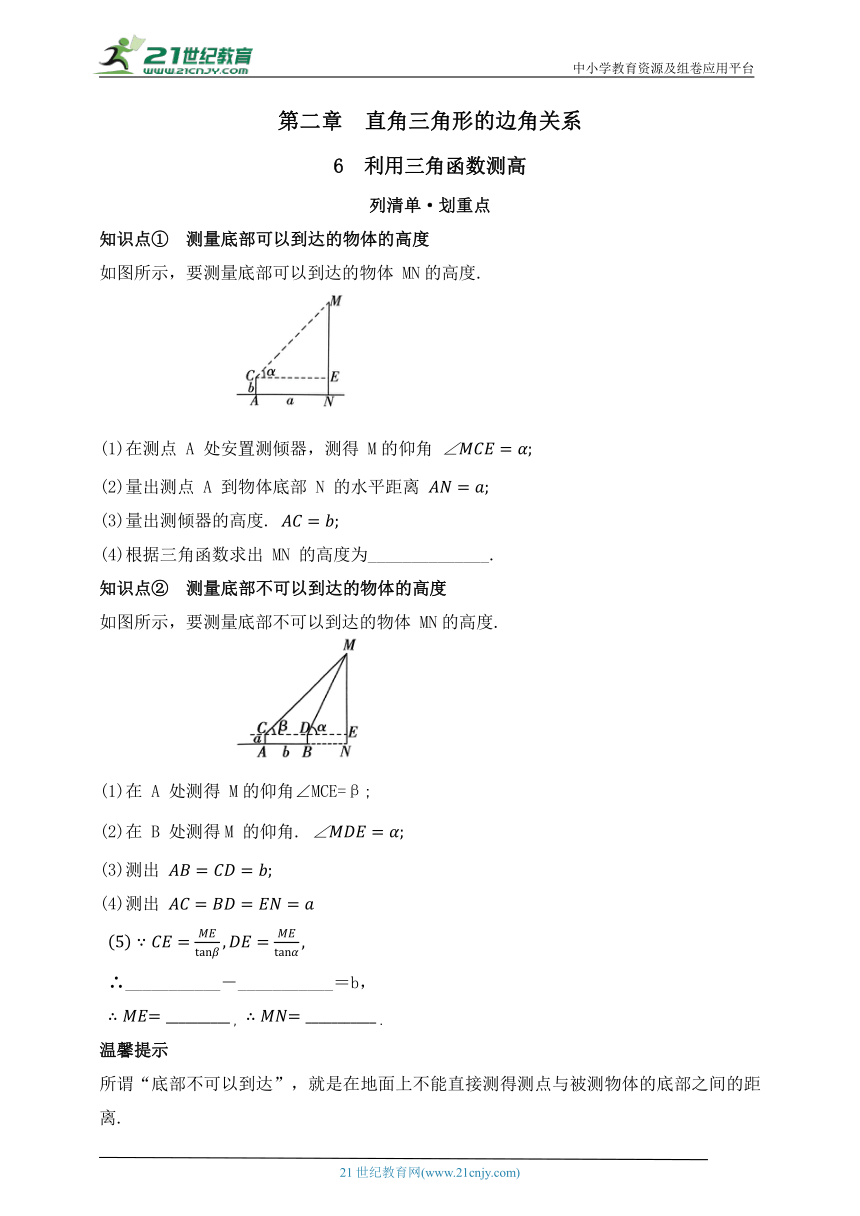 | |
| 格式 | docx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-04 20:25:24 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
6 利用三角函数测高
列清单·划重点
知识点① 测量底部可以到达的物体的高度
如图所示,要测量底部可以到达的物体 MN的高度.
(1)在测点 A 处安置测倾器,测得 M的仰角
(2)量出测点 A 到物体底部 N 的水平距离
(3)量出测倾器的高度.
(4)根据三角函数求出 MN 的高度为______________.
知识点② 测量底部不可以到达的物体的高度
如图所示,要测量底部不可以到达的物体 MN的高度.
(1)在 A 处测得 M的仰角∠MCE=β;
(2)在 B 处测得M 的仰角.
(3)测出
(4)测出
∴___________-___________=b,
温馨提示
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体的底部之间的距离.
明考点·识方法
考点① 测量底部可以到达的物体的高度
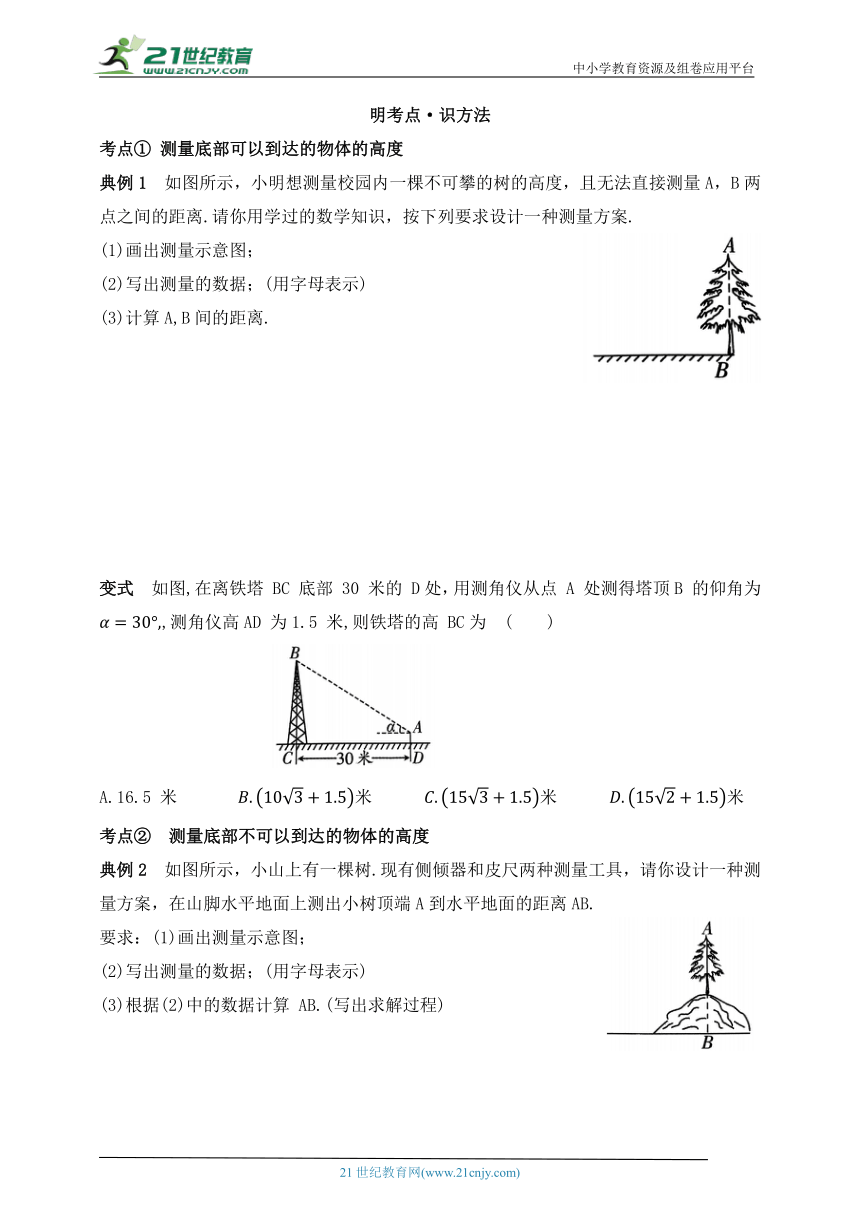
典例1 如图所示,小明想测量校园内一棵不可攀的树的高度,且无法直接测量A,B两点之间的距离.请你用学过的数学知识,按下列要求设计一种测量方案.
(1)画出测量示意图;
(2)写出测量的数据;(用字母表示)
(3)计算A,B间的距离.
变式 如图,在离铁塔 BC 底部 30 米的 D处,用测角仪从点 A 处测得塔顶B 的仰角为 ,测角仪高AD 为1.5 米,则铁塔的高 BC为 ( )
A.16.5 米 米 米 米
考点② 测量底部不可以到达的物体的高度
典例2 如图所示,小山上有一棵树.现有侧倾器和皮尺两种测量工具,请你设计一种测量方案,在山脚水平地面上测出小树顶端A到水平地面的距离AB.
要求:(1)画出测量示意图;
(2)写出测量的数据;(用字母表示)
(3)根据(2)中的数据计算 AB.(写出求解过程)
变式 某综合实践研究小组为了测量观察目标时的仰角和俯角,利用量角器和铅锤自制了一个简易测角仪,如图1所示.
(1)如图2,在 P 点观察所测物体最高点C,当量角器零刻度线上 A,B 两点均在视线PC 上时,测得视线与铅垂线所夹的锐角为α,设仰角为β,请直接用含α的代数式表示β;
(2)如图3,为了测量广场上空气球 A 离地面的高度,该小组利用自制简易测角仪在点 B,C分别测得气球A 的仰角 为为 地面上点 B,C,D在同一水平直线上,求气球 A 离地面的高度 AD.(参考数据:
当堂测·夯基础
1.“儿童放学归来早,忙趁东风放纸鸢”,小朋周末在公园草坪上放风筝,已知风筝拉线长80 米且拉线与地面夹角为 64°(如图所示,假设拉线是直的,小朋身高忽略不计),则风筝离地面的高度可以表示为 ( )
第1题图 第2题图
2.如图,某数学实践小组测量操场的旗杆 AB 的高度,操作如下:(1)在点 D 处放置测角仪,量得测角仪的高度CD为a;(2)测得仰角∠ACE=α;(3)量得测角仪到旗杆的水平距离 BD为b.则旗杆的高度可表示为 ( )
3.徐州电视塔为徐州市的标志性建筑之一,如图,为了测量其高度,小明在云龙公园的点 C 处,用测角仪测得塔顶 A的仰角. 他在平地上沿正对电视塔的方向后退至点 D 处,测得塔顶 A 的仰角. 若测角仪距 地 面 的高度. 求电视塔的高度 AB.(精确到 0. 1 m,参考数据:
参考答案
【列清单·划重点】
知识点1
知识点2
【明考点·识方法】
典例1
解:(答案不唯一)(1)测量示意图如图所示;
(2)测量出.
变式 B
典例2
解:(1)测量示意图如图所示;
(2)测量出∠AHE=α,CD=m,∠AFE=β,HC=FD=h;
(3)设 AE=x.
又
∵HF=HE-EF=CD=m, 解得
变式 解: (1)β=90°-α;
(2)设AD=xm,
∵∠ACD=45°,∠ADB=90°,∴CD=AD=xm,
∵BC=20m,∴BD=(20+x)m,
在 Rt△ABD 中,
即 解得x=60,
经检验,x=60是分式方程的解,∴AD=60(m),
所以,气球A 离地面的高度AD 是 60 m.
【当堂测·夯基础】
1. A 2. A
3.解:由题意,得GE⊥AB,EB=FC=GD=1.6m ,FG=CD=70 m,EF=BC,
设 EF=BC=x m,∴GE=EF+FG=(x+70)m,
在 Rt△AEG 中,∠AGE=30°,∴AE=EG·tan30°≈0.58(x+70)m,
在 Rt△AEF中,∠AFE=36°,∴AE=EF·tan36°≈0.73x(m),
∴0.73x=0.58(x+70),解得x≈270.67,
∴AE=0.73x≈197.59(m),
∴AB = AE + BE = 197.59 +1.6≈199.2(m),
所以,电视塔的高度AB 约为 199.2m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 直角三角形的边角关系
6 利用三角函数测高
列清单·划重点
知识点① 测量底部可以到达的物体的高度
如图所示,要测量底部可以到达的物体 MN的高度.
(1)在测点 A 处安置测倾器,测得 M的仰角
(2)量出测点 A 到物体底部 N 的水平距离
(3)量出测倾器的高度.
(4)根据三角函数求出 MN 的高度为______________.
知识点② 测量底部不可以到达的物体的高度
如图所示,要测量底部不可以到达的物体 MN的高度.
(1)在 A 处测得 M的仰角∠MCE=β;
(2)在 B 处测得M 的仰角.
(3)测出
(4)测出
∴___________-___________=b,
温馨提示
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体的底部之间的距离.
明考点·识方法
考点① 测量底部可以到达的物体的高度
典例1 如图所示,小明想测量校园内一棵不可攀的树的高度,且无法直接测量A,B两点之间的距离.请你用学过的数学知识,按下列要求设计一种测量方案.
(1)画出测量示意图;
(2)写出测量的数据;(用字母表示)
(3)计算A,B间的距离.
变式 如图,在离铁塔 BC 底部 30 米的 D处,用测角仪从点 A 处测得塔顶B 的仰角为 ,测角仪高AD 为1.5 米,则铁塔的高 BC为 ( )
A.16.5 米 米 米 米
考点② 测量底部不可以到达的物体的高度
典例2 如图所示,小山上有一棵树.现有侧倾器和皮尺两种测量工具,请你设计一种测量方案,在山脚水平地面上测出小树顶端A到水平地面的距离AB.
要求:(1)画出测量示意图;
(2)写出测量的数据;(用字母表示)
(3)根据(2)中的数据计算 AB.(写出求解过程)
变式 某综合实践研究小组为了测量观察目标时的仰角和俯角,利用量角器和铅锤自制了一个简易测角仪,如图1所示.
(1)如图2,在 P 点观察所测物体最高点C,当量角器零刻度线上 A,B 两点均在视线PC 上时,测得视线与铅垂线所夹的锐角为α,设仰角为β,请直接用含α的代数式表示β;
(2)如图3,为了测量广场上空气球 A 离地面的高度,该小组利用自制简易测角仪在点 B,C分别测得气球A 的仰角 为为 地面上点 B,C,D在同一水平直线上,求气球 A 离地面的高度 AD.(参考数据:
当堂测·夯基础
1.“儿童放学归来早,忙趁东风放纸鸢”,小朋周末在公园草坪上放风筝,已知风筝拉线长80 米且拉线与地面夹角为 64°(如图所示,假设拉线是直的,小朋身高忽略不计),则风筝离地面的高度可以表示为 ( )
第1题图 第2题图
2.如图,某数学实践小组测量操场的旗杆 AB 的高度,操作如下:(1)在点 D 处放置测角仪,量得测角仪的高度CD为a;(2)测得仰角∠ACE=α;(3)量得测角仪到旗杆的水平距离 BD为b.则旗杆的高度可表示为 ( )
3.徐州电视塔为徐州市的标志性建筑之一,如图,为了测量其高度,小明在云龙公园的点 C 处,用测角仪测得塔顶 A的仰角. 他在平地上沿正对电视塔的方向后退至点 D 处,测得塔顶 A 的仰角. 若测角仪距 地 面 的高度. 求电视塔的高度 AB.(精确到 0. 1 m,参考数据:
参考答案
【列清单·划重点】
知识点1
知识点2
【明考点·识方法】
典例1
解:(答案不唯一)(1)测量示意图如图所示;
(2)测量出.
变式 B
典例2
解:(1)测量示意图如图所示;
(2)测量出∠AHE=α,CD=m,∠AFE=β,HC=FD=h;
(3)设 AE=x.
又
∵HF=HE-EF=CD=m, 解得
变式 解: (1)β=90°-α;
(2)设AD=xm,
∵∠ACD=45°,∠ADB=90°,∴CD=AD=xm,
∵BC=20m,∴BD=(20+x)m,
在 Rt△ABD 中,
即 解得x=60,
经检验,x=60是分式方程的解,∴AD=60(m),
所以,气球A 离地面的高度AD 是 60 m.
【当堂测·夯基础】
1. A 2. A
3.解:由题意,得GE⊥AB,EB=FC=GD=1.6m ,FG=CD=70 m,EF=BC,
设 EF=BC=x m,∴GE=EF+FG=(x+70)m,
在 Rt△AEG 中,∠AGE=30°,∴AE=EG·tan30°≈0.58(x+70)m,
在 Rt△AEF中,∠AFE=36°,∴AE=EF·tan36°≈0.73x(m),
∴0.73x=0.58(x+70),解得x≈270.67,
∴AE=0.73x≈197.59(m),
∴AB = AE + BE = 197.59 +1.6≈199.2(m),
所以,电视塔的高度AB 约为 199.2m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
