第二章 直角三角形的边角关系 5 三角函数的应用 第1课时 仰角、俯角问题
文档属性
| 名称 | 第二章 直角三角形的边角关系 5 三角函数的应用 第1课时 仰角、俯角问题 |

|
|
| 格式 | docx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-04 20:27:13 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
5 三角函数的应用
第1课时 仰角、俯角问题
列清单·划重点
知识点① 仰角与俯角
示意图 仰角与俯角
仰角: (如图所示)当从_______观测高处的目标时,视线与水平线所成的锐角
俯角:(如图所示)当从________观测低处的目标时,视线与水平线所成的锐角
注意
仰角、俯角是视线与水平线所成的锐角,不要误认为视线与铅垂线所成的锐角.
知识点② 运用解直角三角形的知识解决生产、生活中实际问题的步骤
一审:弄清题意,找出已知量和未知量;
二构:根据题意,画出示意图,并构造要求解的三角形,对非直角三角形通过作辅助线构造直角三角形“化斜为直”;
三选:将题中的已知角、线段转变为直角三角形的元素,选择恰当的元素间的关系式,解直角三角形;
四答:按照题中已知量的精确度或题中要求的精确度给出答案并注明单位;如题中未明确精确度,结果可保留最简根式的形式.
明考点·识方法
考点 与仰角、俯角有关的实际问题
典例 根据以下材料,完成项目任务.
项目 测量古塔的高度及古塔底面圆的半径
测量工具 测角仪、皮尺等
测量 图示:
说明:点 Q 为古塔底面圆圆心,测角仪高度AB=CD=1.5m,在B,D 处分别测得古塔顶端的仰角为32°,45°,BD=9 m,测角仪CD 所在位置与古塔底部边缘距离 DG=12.9 m.点 B,D,G,Q在同一条直线上
参考数据 sin32°≈0.530,cos32°≈0.848,tan32°≈ 0.625
项目任务:
(1)求出古塔的高度;
(2)求出古塔底面圆的半径.
思路导析 本题考查解直角三角形的应用——仰角、俯角问题、矩形的判定与性质、等腰直角三角形的判定与性质、锐角三角函数的定义等知识,熟练掌握锐角三角函数的定义是解题的关键.首先延长AC交PQ 于点H,则四边形CDQH、四边形ABQH 都为矩形,得出对边相等,设古塔底面圆的半径为x m,找等量关系,列方程,求x,则在Rt△PAH中可以求出两条直角边的值,最后再由PQ=PH+QH,即可得出答案.
变式 “科技改变生活”,小王是一名摄影爱好者,新入手了一台无人机用于航拍.在一次航拍时,数据显示,从无人机 A 看建筑物顶部B 的仰角为 看底部 C的俯角为 无人机 A到该建筑物BC 的水平距离AD 为 10 米,求该建筑物BC 的高度.(结果精确到 0.1 米;参考数据:
当堂测·夯基础
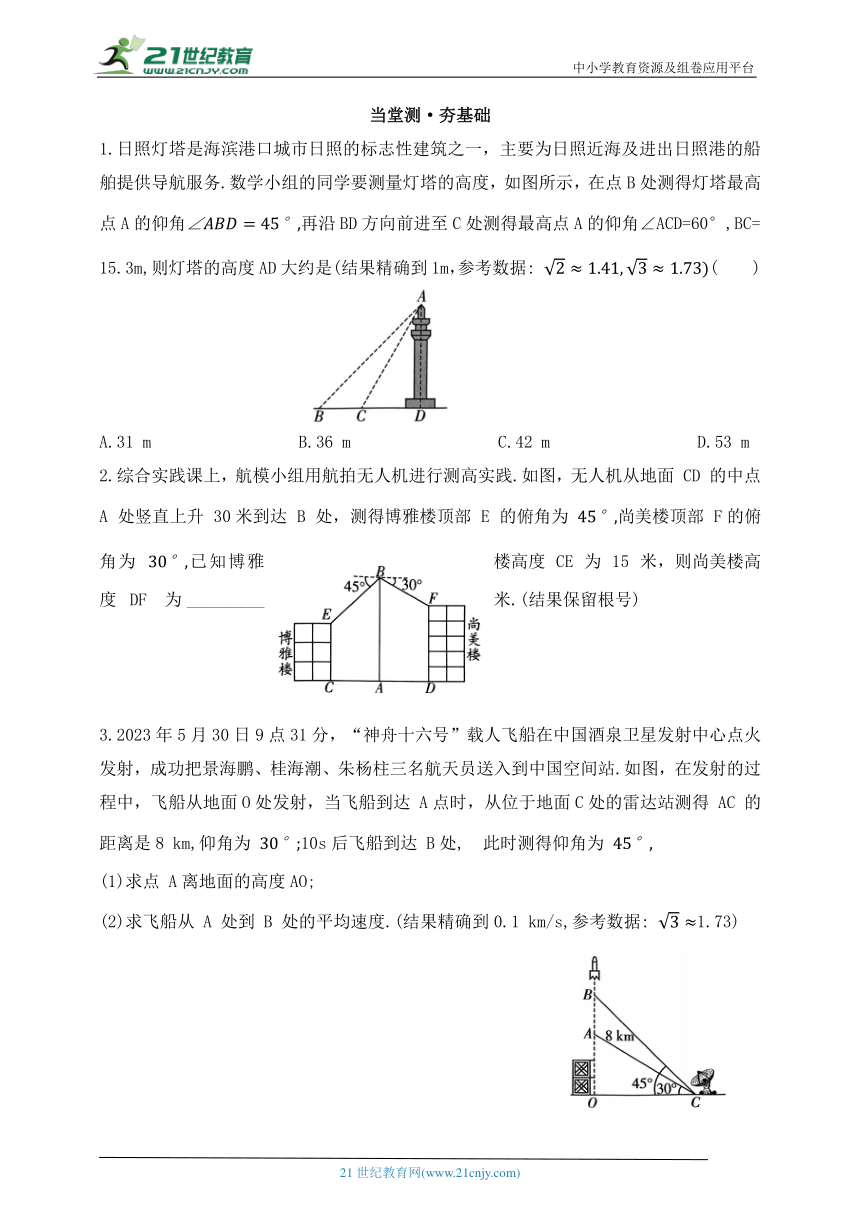
1.日照灯塔是海滨港口城市日照的标志性建筑之一,主要为日照近海及进出日照港的船舶提供导航服务.数学小组的同学要测量灯塔的高度,如图所示,在点B处测得灯塔最高点A的仰角再沿BD方向前进至C处测得最高点A的仰角∠ACD=60°,BC=
15.3m,则灯塔的高度AD大约是(结果精确到1m,参考数据: ( )
A.31 m B.36 m C.42 m D.53 m
2.综合实践课上,航模小组用航拍无人机进行测高实践.如图,无人机从地面 CD 的中点 A 处竖直上升 30米到达 B 处,测得博雅楼顶部 E 的俯角为 尚美楼顶部 F的俯角为 已知博雅楼高度 CE 为 15 米,则尚美楼高度DF 为_________米.(结果保留根号)
3.2023年5月30日9点31分,“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射,成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站.如图,在发射的过程中,飞船从地面O处发射,当飞船到达 A点时,从位于地面C处的雷达站测得 AC 的距离是8 km,仰角为 10s后飞船到达 B处, 此时测得仰角为
(1)求点 A离地面的高度AO;
(2)求飞船从 A 处到 B 处的平均速度.(结果精确到0.1 km/s,参考数据: 1.73)
参考答案
【列清单·划重点】
知识点1 低处 高处
【明考点·识方法】
典例 解:如图,延长 AC 交 PQ 于点 H,则四边形CDQH、四边形 ABQH 都为矩形,
∴CH=DQ,BQ=AH, ∠PHA =90°, AB = QH =1.5m,
由题意,得∠PAH=32°,∠PCH=45°,古塔的高度为 PQ,古塔底面圆的半径为GQ,
∴△PHC 是等腰直角三角形,∴PH=CH,
设GQ=xm,则PH=CH=DQ=DG+GQ=(12.9+x)m,
∴AH=BQ=BD+DQ=9+12.9+x=(21.9+x)m,
在 Rt△PHA 中,PH=AH·tan∠PAH=AH·tan32°≈0.625(21.9+x)=(13.687 5+0.625x)m,
∴12.9+x=13.687 5+0.625x,解得x=2.1,
∴PQ=PH+QH=12.9+2.1+1.5=16.5m,
所以,古塔的高度为16.5m ,古塔底面圆的半径为2.1m .
变式 解:由题意,得∠BAD=45°,∠CAD=60°,AD⊥BC.
∵AD⊥BC,∴∠BDA=∠ADC=90°,∴∠BAD=∠ABD=45°,∴BD=AD=10(米).
在 Rt△ACD 中,CD= AD·tan∠CAD= AD·tan60°=(米).
(米).
所以,该建筑物 BC的高度约为 27.3米.
【当堂测·夯基础】
1. B
3.解:(1)在 中,
(2)在 中,
在 中,
∴飞船从 A 处到 B 处的平均速度 =
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 直角三角形的边角关系
5 三角函数的应用
第1课时 仰角、俯角问题
列清单·划重点
知识点① 仰角与俯角
示意图 仰角与俯角
仰角: (如图所示)当从_______观测高处的目标时,视线与水平线所成的锐角
俯角:(如图所示)当从________观测低处的目标时,视线与水平线所成的锐角
注意
仰角、俯角是视线与水平线所成的锐角,不要误认为视线与铅垂线所成的锐角.
知识点② 运用解直角三角形的知识解决生产、生活中实际问题的步骤
一审:弄清题意,找出已知量和未知量;
二构:根据题意,画出示意图,并构造要求解的三角形,对非直角三角形通过作辅助线构造直角三角形“化斜为直”;
三选:将题中的已知角、线段转变为直角三角形的元素,选择恰当的元素间的关系式,解直角三角形;
四答:按照题中已知量的精确度或题中要求的精确度给出答案并注明单位;如题中未明确精确度,结果可保留最简根式的形式.
明考点·识方法
考点 与仰角、俯角有关的实际问题
典例 根据以下材料,完成项目任务.
项目 测量古塔的高度及古塔底面圆的半径
测量工具 测角仪、皮尺等
测量 图示:
说明:点 Q 为古塔底面圆圆心,测角仪高度AB=CD=1.5m,在B,D 处分别测得古塔顶端的仰角为32°,45°,BD=9 m,测角仪CD 所在位置与古塔底部边缘距离 DG=12.9 m.点 B,D,G,Q在同一条直线上
参考数据 sin32°≈0.530,cos32°≈0.848,tan32°≈ 0.625
项目任务:
(1)求出古塔的高度;
(2)求出古塔底面圆的半径.
思路导析 本题考查解直角三角形的应用——仰角、俯角问题、矩形的判定与性质、等腰直角三角形的判定与性质、锐角三角函数的定义等知识,熟练掌握锐角三角函数的定义是解题的关键.首先延长AC交PQ 于点H,则四边形CDQH、四边形ABQH 都为矩形,得出对边相等,设古塔底面圆的半径为x m,找等量关系,列方程,求x,则在Rt△PAH中可以求出两条直角边的值,最后再由PQ=PH+QH,即可得出答案.
变式 “科技改变生活”,小王是一名摄影爱好者,新入手了一台无人机用于航拍.在一次航拍时,数据显示,从无人机 A 看建筑物顶部B 的仰角为 看底部 C的俯角为 无人机 A到该建筑物BC 的水平距离AD 为 10 米,求该建筑物BC 的高度.(结果精确到 0.1 米;参考数据:
当堂测·夯基础
1.日照灯塔是海滨港口城市日照的标志性建筑之一,主要为日照近海及进出日照港的船舶提供导航服务.数学小组的同学要测量灯塔的高度,如图所示,在点B处测得灯塔最高点A的仰角再沿BD方向前进至C处测得最高点A的仰角∠ACD=60°,BC=
15.3m,则灯塔的高度AD大约是(结果精确到1m,参考数据: ( )
A.31 m B.36 m C.42 m D.53 m
2.综合实践课上,航模小组用航拍无人机进行测高实践.如图,无人机从地面 CD 的中点 A 处竖直上升 30米到达 B 处,测得博雅楼顶部 E 的俯角为 尚美楼顶部 F的俯角为 已知博雅楼高度 CE 为 15 米,则尚美楼高度DF 为_________米.(结果保留根号)
3.2023年5月30日9点31分,“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射,成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站.如图,在发射的过程中,飞船从地面O处发射,当飞船到达 A点时,从位于地面C处的雷达站测得 AC 的距离是8 km,仰角为 10s后飞船到达 B处, 此时测得仰角为
(1)求点 A离地面的高度AO;
(2)求飞船从 A 处到 B 处的平均速度.(结果精确到0.1 km/s,参考数据: 1.73)
参考答案
【列清单·划重点】
知识点1 低处 高处
【明考点·识方法】
典例 解:如图,延长 AC 交 PQ 于点 H,则四边形CDQH、四边形 ABQH 都为矩形,
∴CH=DQ,BQ=AH, ∠PHA =90°, AB = QH =1.5m,
由题意,得∠PAH=32°,∠PCH=45°,古塔的高度为 PQ,古塔底面圆的半径为GQ,
∴△PHC 是等腰直角三角形,∴PH=CH,
设GQ=xm,则PH=CH=DQ=DG+GQ=(12.9+x)m,
∴AH=BQ=BD+DQ=9+12.9+x=(21.9+x)m,
在 Rt△PHA 中,PH=AH·tan∠PAH=AH·tan32°≈0.625(21.9+x)=(13.687 5+0.625x)m,
∴12.9+x=13.687 5+0.625x,解得x=2.1,
∴PQ=PH+QH=12.9+2.1+1.5=16.5m,
所以,古塔的高度为16.5m ,古塔底面圆的半径为2.1m .
变式 解:由题意,得∠BAD=45°,∠CAD=60°,AD⊥BC.
∵AD⊥BC,∴∠BDA=∠ADC=90°,∴∠BAD=∠ABD=45°,∴BD=AD=10(米).
在 Rt△ACD 中,CD= AD·tan∠CAD= AD·tan60°=(米).
(米).
所以,该建筑物 BC的高度约为 27.3米.
【当堂测·夯基础】
1. B
3.解:(1)在 中,
(2)在 中,
在 中,
∴飞船从 A 处到 B 处的平均速度 =
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
