2023~2024学年广东深圳福田区福田区高级中学高一上学期期中数学试卷(PDF版含解析)
文档属性
| 名称 | 2023~2024学年广东深圳福田区福田区高级中学高一上学期期中数学试卷(PDF版含解析) |

|
|
| 格式 | |||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-04 00:00:00 | ||
图片预览




文档简介
2023~2024学年广东深圳福田区福田区高级中学高一上学期期中数学试卷
一、单选题(本大题共8小题,每小题5分,共40分)
1、设集合 ,集合 ,则 ( )
A.
B.
C.
D.
2、如图所示,①②③④中不属于函数 的一个是( ).
A.①
B.②
C.③
D.④
3、已知函数 ,则 ( )
A.
B.
C.2
D.
4、已知幂函数 的图像过点 ,则下列结论正确的是( )
A. 的定义域为
B. 在其定义域内为减函数
C. 是偶函数
D. 是奇函数
5、若 , , ,则( )
A.
B.
C.
D.
6、已知不等式 的解集为空集,则a的取值范围是( )
A.
B.
C. 或
D. 或
7、已知函数 ,则不等式 的解集为( )
A.
B.
C.
D.
8、已知函数 ,对于定义域内任意的 ,下述四个结论中:
① ②
③ ④
其中错误的个数是( )
A.1
B.2
C.3
D.4
二、多选题(本大题共4小题,每小题5分,共20分)
9、“ ”的一个充分不必要条件可以是( )
A.
B.
C.
D.
10、下列命题中,正确的是( )
A.若 ,则
B.若 , ,则
C.若 , ,则
D.若 , ,则
11、若正实数 、 满足 ,则下列说法正确的是( )
A. 有最大值
B. 有最大值
C. 有最小值
D. 有最大值
12、已知函数 的定义域为 , 为奇函数, 为偶函数,当 时, ,则以
下结论正确的有( )
A.点 不是 的图象的对称中心
B. ,
C.当 时,
D.
三、填空题(本大题共4小题,每小题5分,共20分)
13、命题“ , ”的否定是 .
14、函数 的单调递减区间是 .
15、已知 是定义在 上的偶函数,且在 上递减,则不等式 的解集
是 .
16、已知指数函数 ( 且 )在其定义域内单调递增.设函数
,当 时,函数 恒成立,则x的取值范围是 .
四、解答题(本大题共6小题,共70分)
17、(本小题10分)
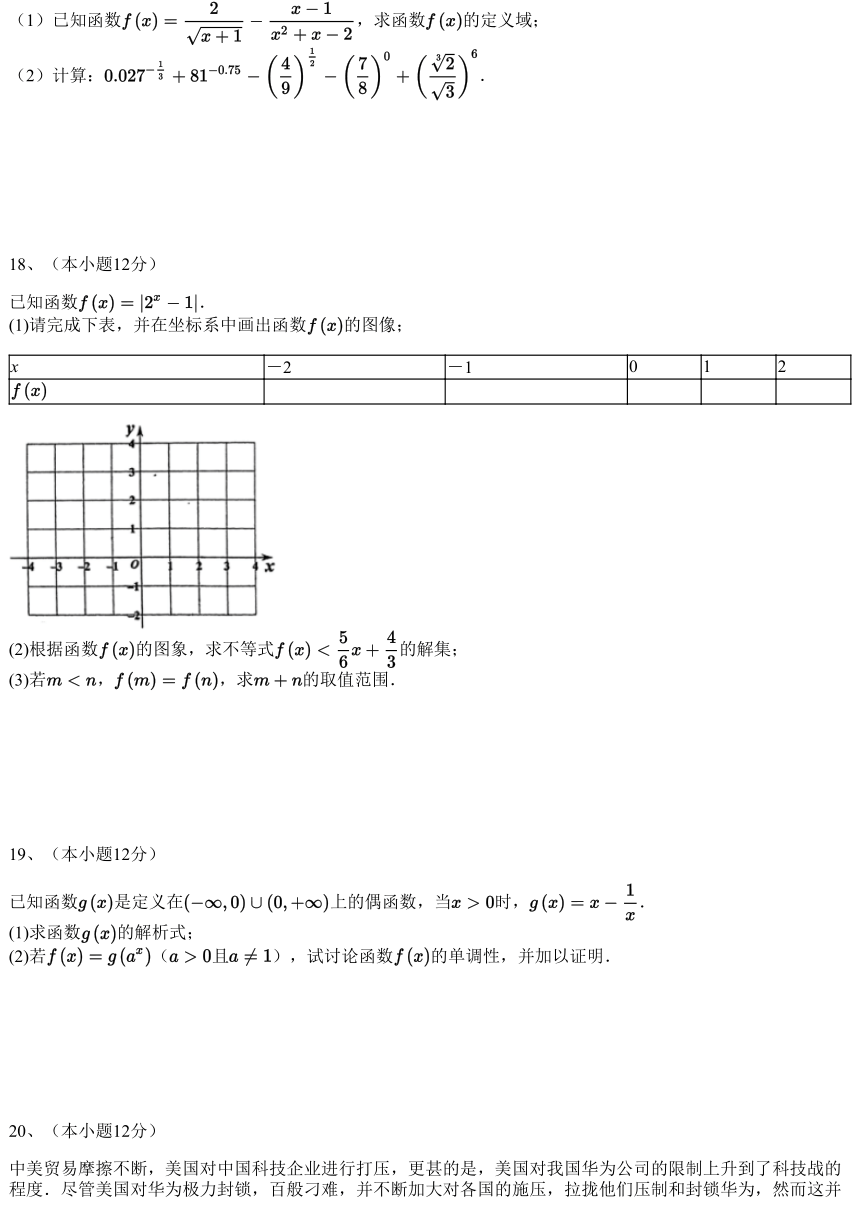
(1)已知函数 ,求函数 的定义域;
(2)计算: .
18、(本小题12分)
已知函数 .
(1)请完成下表,并在坐标系 中画出函数 的图像;
x -2 -1 0 1 2
(2)根据函数 的图象,求不等式 的解集;
(3)若 , ,求 的取值范围.
19、(本小题12分)
已知函数 是定义在 上的偶函数,当 时, .
(1)求函数 的解析式;
(2) 若 ( 且 ),试讨论函数 的单调性,并加以证明.
20、(本小题12分)
中美贸易摩擦不断,美国对中国科技企业进行打压,更甚的是,美国对我国华为公司的限制上升到了科技战的
程度.尽管美国对华为极力封锁,百般刁难,并不断加大对各国的施压,拉拢他们压制和封锁华为,然而这并
没有让华为却步.华为及中国科技者经过三年多的努力,终于在今年取得突破.今年,我国某一企业为了进一
步增加市场竞争力,计划在2024年利用新技术生产某款新手机.通过市场分析,生产此款手机全年需投入固定
成本500万元,每生产x(千部)手机,需另投入成本 万元,且
,由市场调研知,每部手机售价0.7万元,且全年内生产的手机当年能全部销售完.
(1)求2024年的利润 (万元)关于年产量x(千部)的函数关系式,(利润 销售 额 成本);
(2)2024年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
21、(本小题12分)
设集合 ,B a .①若 < ,
=R,求a、b的值;②若b= ,且A =A,求实数a的取值范围.
22、(本小题12分)
已知函数 有如下性质:如果常数 ,那么该函数在 上是减函数,在 上是增函
数.
(1)已知 ,利用上述性质,求函数 的单调区间和值域;
(2)当 时,对于(1)中的函数 和函数 ,若对 , ,使得
成立,求实数a的取值范围.
参考答案
一、单选题
1、
<答 案>:
C
<解析>:
因为 ,所以 ,
且 ,所以 = .
故选:C
2、
<答 案>:
B
<解析>:
根据函数图象可判断②不过点 ,又指数函数恒过定点 即可判断.
解:已知其中的三个函数都是指数函数,指数函数的图象一定过点 , 图象②不过点 .
故选:
3、
<答 案>:
B
<解析>:
因为 ,且 ,
所以 ,
所以 ,
故选:B.
4、
<答 案>:
B
<解析>:
设 ,代入点 可得 ,所以 ,
所以 ,
对于A:函数的定义域为 ,所以A错误;
对于B:因为 ,所以 在 内单调递减,B正确;
对于C:因为 的定义域为 ,所以不是偶函数,C错误;
对于D:因为 的定义域为 ,所以不是奇函数,D错误,
故选:B
5、
<答 案>:
A
<解析>:
由指数函数单调性知, ,即
又 ,即 ,故 ,
因此正确答案为:A.
6、
<答 案>:
A
<解析>:
由不等式 的解集为空集,
根据二次函数的性质,则满足 ,解得 .
即实数 的取值范围是 .
故选:A.
7、
<答 案>:
D
<解析>:
如图:
根据函数图象,及 可知: ,
得 或 ,
故选:D
8、
<答 案>:
A
<解析>:
对于①. ,故①错
对于②. ,
,
所以 ,故②正确;
对于③. ,而 ,
令 , ,故 ,
而 ,故 ,
所以 ,故 ,故③正确
对于④. 由 为减函数,可得 ,故④
正确
故选 :A.
二、多选题
9、
<答 案>:
B;C
<解析>:
,所以 .
设 ,设选项对应的集合为 ,
因为选项是“ ”的一个充分不必要条件,
所以 是 的真子集.
故选:BC.
10、
<答案 >:
B;C
<解析>:
对于A,由 可得 ,即 或 ,故A不正确;
对于B,因为 , ,所以 , ,故B正确;
对于C,因为 ,所以 ,因为 ,所以 ,故C正确;
对于D, ,因为 , ,所以 ,故
D不正确.
故选:BC .
11、
<答案 >:
A;B;C
<解析>:
因为正实数 、 满足 ,
对于A选项, ,
当且仅当 时,即当 时,等号成立,
所以, 有最大值 ,A对;
对于B选项, ,则 ,
当且仅当 时,即当 时,等号成立,
即 有最大值 ,B对;
对于C选项, ,
当且仅当 时,即当 时,等号成立,即 有最小值 ,C对;
对于D选项,因为 ,所以, ,
即 ,当且仅当 时,即当 时,等号成立,
所以, 有最小值 ,D错.
故选:ABC.
12、
<答案 >:
B;C;D
<解析>:
对于B选项,因为 为奇函数,则 ,即 ,
,
又因为 为偶函数,则 ,即 ,
所以, ,B对;
对于A选项, ,即 ,
所以,点 是 的图象的对称中心,A错;
对于C选项,当 时, ,则 ,
所以,对任意的 , ,
所以,当 时, ,
则 ,
故当 时, ,
所以, ,C对;
对于D选项, ,D对.
故选:BCD.
三、填空题
13、
<答案 >:
,
<解析>:
因为特称(存在)量词命题的否定是全称量词命题,
所以命题 , 的否定是 ,
故答案为: ,
14、
<答案 >:
<解析>:
对于函数 ,有 ,解得 ,
所以,函数 的定义域为 ,
因为内层函数 在 上为减函数,在 上为增函数,且 ,
外层函数 在 上为减函数,
所以,函数 的单调递减区间为 .
故答案为: .
15、
<答案 >:
<解析>:
解:因为 是定义在 上的偶函数,且在 上递减,
所以 在 上递增,
不等式 等价于 ,
所以 ,解得 ,
所以不等式 的解集是 .
故答案为:
16、
<答案 >:
<解析>:
因为 是指数函数,所以 ,解得 或者 ,
又因为 在定义域内单调递增,所以 ,所以 ,所以 ,
所以 ,
令 ,要使得 即 恒成立,
则 ,
所以 ,解得 ,
故答案为:
四、解答题
17、
<答案 >:
(1) ;(2) .
<解析>:
解:(1)对于函数 ,有 ,解得 且 ,
所以,函数 的定义域为 ;
(2)原式
.
18、
<答案 >:
(1)详见解析
(2)
(3)
<解析>:
(1)解:
x -2 -1 0 1 2
0 1 3
的图象,如图所示:
(2)如图所示:
由图象知: 时, ;
(3)因为 , ,
所以 ,
则 , ,即 ,
所以 ,则 ,
所以 的取值范围是 .
19、
<答案 >:
(1)
(2)答案及证明见解析
<解析>:
(1)解:由题意,∵函数 是定义在 上的偶函数,
当 时, ,
∴当 时, ,则 ,
∴ .
(2)证明:∵由指数函数的图象与性质知,当 且 时,对 , ,
∴ , ,
设 ,则
,
当 时, ,则 ,即 ,
函数 单调递减;
当 时, ,则 ,即 ,
函数 单调递增;
综上知,当 时,函数 单调递减;当 时,函数 单调递增.
20、
<答案 >:
(1)
(2)产量 千部时,利润取得最大值7750万元.
<解析>:
(1)由题意可知 ,
(2)当 时, ,
当且仅当 时取得最大值7500;
当 时, ,
当且仅当 时,取得最大值7750,显然 ,
综上:当 时,取得最大值7750.
21、
<答案 >:
<解析>:
由题设知
设
①由 < ,得 从而,
②因为 ,所以,
当 时,由 < ,得 < <
当 时,若 ,则
当 时, ,不符合题 意;
当 时, ,符合题意.
>
若 > ,则 .综上, <
-
22、
<答案 >:
(1)值域为 ,单调增区间为 ,单调减区间为
(2)
<解析>:
(1)因为 ,
设 , ,则 .
令 , .
又由已知性质可得 在 单调递减,在 单调递增,
又∵ , , ,
∴ ,
∴ 的值域为 ,单调增区间为 ,单调减区间为
(2)因为 , ,任取 ,
则
,
即 ,所以 在 单调递减,
则 , ,
所以 ,
1 由( )可知,当 时, ,
因为对 , ,使得 成立,
所以 的值域是 值域的子集,
则 ,解得 ,
所以实数a的取值范围为 .
一、单选题(本大题共8小题,每小题5分,共40分)
1、设集合 ,集合 ,则 ( )
A.
B.
C.
D.
2、如图所示,①②③④中不属于函数 的一个是( ).
A.①
B.②
C.③
D.④
3、已知函数 ,则 ( )
A.
B.
C.2
D.
4、已知幂函数 的图像过点 ,则下列结论正确的是( )
A. 的定义域为
B. 在其定义域内为减函数
C. 是偶函数
D. 是奇函数
5、若 , , ,则( )
A.
B.
C.
D.
6、已知不等式 的解集为空集,则a的取值范围是( )
A.
B.
C. 或
D. 或
7、已知函数 ,则不等式 的解集为( )
A.
B.
C.
D.
8、已知函数 ,对于定义域内任意的 ,下述四个结论中:
① ②
③ ④
其中错误的个数是( )
A.1
B.2
C.3
D.4
二、多选题(本大题共4小题,每小题5分,共20分)
9、“ ”的一个充分不必要条件可以是( )
A.
B.
C.
D.
10、下列命题中,正确的是( )
A.若 ,则
B.若 , ,则
C.若 , ,则
D.若 , ,则
11、若正实数 、 满足 ,则下列说法正确的是( )
A. 有最大值
B. 有最大值
C. 有最小值
D. 有最大值
12、已知函数 的定义域为 , 为奇函数, 为偶函数,当 时, ,则以
下结论正确的有( )
A.点 不是 的图象的对称中心
B. ,
C.当 时,
D.
三、填空题(本大题共4小题,每小题5分,共20分)
13、命题“ , ”的否定是 .
14、函数 的单调递减区间是 .
15、已知 是定义在 上的偶函数,且在 上递减,则不等式 的解集
是 .
16、已知指数函数 ( 且 )在其定义域内单调递增.设函数
,当 时,函数 恒成立,则x的取值范围是 .
四、解答题(本大题共6小题,共70分)
17、(本小题10分)
(1)已知函数 ,求函数 的定义域;
(2)计算: .
18、(本小题12分)
已知函数 .
(1)请完成下表,并在坐标系 中画出函数 的图像;
x -2 -1 0 1 2
(2)根据函数 的图象,求不等式 的解集;
(3)若 , ,求 的取值范围.
19、(本小题12分)
已知函数 是定义在 上的偶函数,当 时, .
(1)求函数 的解析式;
(2) 若 ( 且 ),试讨论函数 的单调性,并加以证明.
20、(本小题12分)
中美贸易摩擦不断,美国对中国科技企业进行打压,更甚的是,美国对我国华为公司的限制上升到了科技战的
程度.尽管美国对华为极力封锁,百般刁难,并不断加大对各国的施压,拉拢他们压制和封锁华为,然而这并
没有让华为却步.华为及中国科技者经过三年多的努力,终于在今年取得突破.今年,我国某一企业为了进一
步增加市场竞争力,计划在2024年利用新技术生产某款新手机.通过市场分析,生产此款手机全年需投入固定
成本500万元,每生产x(千部)手机,需另投入成本 万元,且
,由市场调研知,每部手机售价0.7万元,且全年内生产的手机当年能全部销售完.
(1)求2024年的利润 (万元)关于年产量x(千部)的函数关系式,(利润 销售 额 成本);
(2)2024年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
21、(本小题12分)
设集合 ,B a .①若 < ,
=R,求a、b的值;②若b= ,且A =A,求实数a的取值范围.
22、(本小题12分)
已知函数 有如下性质:如果常数 ,那么该函数在 上是减函数,在 上是增函
数.
(1)已知 ,利用上述性质,求函数 的单调区间和值域;
(2)当 时,对于(1)中的函数 和函数 ,若对 , ,使得
成立,求实数a的取值范围.
参考答案
一、单选题
1、
<答 案>:
C
<解析>:
因为 ,所以 ,
且 ,所以 = .
故选:C
2、
<答 案>:
B
<解析>:
根据函数图象可判断②不过点 ,又指数函数恒过定点 即可判断.
解:已知其中的三个函数都是指数函数,指数函数的图象一定过点 , 图象②不过点 .
故选:
3、
<答 案>:
B
<解析>:
因为 ,且 ,
所以 ,
所以 ,
故选:B.
4、
<答 案>:
B
<解析>:
设 ,代入点 可得 ,所以 ,
所以 ,
对于A:函数的定义域为 ,所以A错误;
对于B:因为 ,所以 在 内单调递减,B正确;
对于C:因为 的定义域为 ,所以不是偶函数,C错误;
对于D:因为 的定义域为 ,所以不是奇函数,D错误,
故选:B
5、
<答 案>:
A
<解析>:
由指数函数单调性知, ,即
又 ,即 ,故 ,
因此正确答案为:A.
6、
<答 案>:
A
<解析>:
由不等式 的解集为空集,
根据二次函数的性质,则满足 ,解得 .
即实数 的取值范围是 .
故选:A.
7、
<答 案>:
D
<解析>:
如图:
根据函数图象,及 可知: ,
得 或 ,
故选:D
8、
<答 案>:
A
<解析>:
对于①. ,故①错
对于②. ,
,
所以 ,故②正确;
对于③. ,而 ,
令 , ,故 ,
而 ,故 ,
所以 ,故 ,故③正确
对于④. 由 为减函数,可得 ,故④
正确
故选 :A.
二、多选题
9、
<答 案>:
B;C
<解析>:
,所以 .
设 ,设选项对应的集合为 ,
因为选项是“ ”的一个充分不必要条件,
所以 是 的真子集.
故选:BC.
10、
<答案 >:
B;C
<解析>:
对于A,由 可得 ,即 或 ,故A不正确;
对于B,因为 , ,所以 , ,故B正确;
对于C,因为 ,所以 ,因为 ,所以 ,故C正确;
对于D, ,因为 , ,所以 ,故
D不正确.
故选:BC .
11、
<答案 >:
A;B;C
<解析>:
因为正实数 、 满足 ,
对于A选项, ,
当且仅当 时,即当 时,等号成立,
所以, 有最大值 ,A对;
对于B选项, ,则 ,
当且仅当 时,即当 时,等号成立,
即 有最大值 ,B对;
对于C选项, ,
当且仅当 时,即当 时,等号成立,即 有最小值 ,C对;
对于D选项,因为 ,所以, ,
即 ,当且仅当 时,即当 时,等号成立,
所以, 有最小值 ,D错.
故选:ABC.
12、
<答案 >:
B;C;D
<解析>:
对于B选项,因为 为奇函数,则 ,即 ,
,
又因为 为偶函数,则 ,即 ,
所以, ,B对;
对于A选项, ,即 ,
所以,点 是 的图象的对称中心,A错;
对于C选项,当 时, ,则 ,
所以,对任意的 , ,
所以,当 时, ,
则 ,
故当 时, ,
所以, ,C对;
对于D选项, ,D对.
故选:BCD.
三、填空题
13、
<答案 >:
,
<解析>:
因为特称(存在)量词命题的否定是全称量词命题,
所以命题 , 的否定是 ,
故答案为: ,
14、
<答案 >:
<解析>:
对于函数 ,有 ,解得 ,
所以,函数 的定义域为 ,
因为内层函数 在 上为减函数,在 上为增函数,且 ,
外层函数 在 上为减函数,
所以,函数 的单调递减区间为 .
故答案为: .
15、
<答案 >:
<解析>:
解:因为 是定义在 上的偶函数,且在 上递减,
所以 在 上递增,
不等式 等价于 ,
所以 ,解得 ,
所以不等式 的解集是 .
故答案为:
16、
<答案 >:
<解析>:
因为 是指数函数,所以 ,解得 或者 ,
又因为 在定义域内单调递增,所以 ,所以 ,所以 ,
所以 ,
令 ,要使得 即 恒成立,
则 ,
所以 ,解得 ,
故答案为:
四、解答题
17、
<答案 >:
(1) ;(2) .
<解析>:
解:(1)对于函数 ,有 ,解得 且 ,
所以,函数 的定义域为 ;
(2)原式
.
18、
<答案 >:
(1)详见解析
(2)
(3)
<解析>:
(1)解:
x -2 -1 0 1 2
0 1 3
的图象,如图所示:
(2)如图所示:
由图象知: 时, ;
(3)因为 , ,
所以 ,
则 , ,即 ,
所以 ,则 ,
所以 的取值范围是 .
19、
<答案 >:
(1)
(2)答案及证明见解析
<解析>:
(1)解:由题意,∵函数 是定义在 上的偶函数,
当 时, ,
∴当 时, ,则 ,
∴ .
(2)证明:∵由指数函数的图象与性质知,当 且 时,对 , ,
∴ , ,
设 ,则
,
当 时, ,则 ,即 ,
函数 单调递减;
当 时, ,则 ,即 ,
函数 单调递增;
综上知,当 时,函数 单调递减;当 时,函数 单调递增.
20、
<答案 >:
(1)
(2)产量 千部时,利润取得最大值7750万元.
<解析>:
(1)由题意可知 ,
(2)当 时, ,
当且仅当 时取得最大值7500;
当 时, ,
当且仅当 时,取得最大值7750,显然 ,
综上:当 时,取得最大值7750.
21、
<答案 >:
<解析>:
由题设知
设
①由 < ,得 从而,
②因为 ,所以,
当 时,由 < ,得 < <
当 时,若 ,则
当 时, ,不符合题 意;
当 时, ,符合题意.
>
若 > ,则 .综上, <
-
22、
<答案 >:
(1)值域为 ,单调增区间为 ,单调减区间为
(2)
<解析>:
(1)因为 ,
设 , ,则 .
令 , .
又由已知性质可得 在 单调递减,在 单调递增,
又∵ , , ,
∴ ,
∴ 的值域为 ,单调增区间为 ,单调减区间为
(2)因为 , ,任取 ,
则
,
即 ,所以 在 单调递减,
则 , ,
所以 ,
1 由( )可知,当 时, ,
因为对 , ,使得 成立,
所以 的值域是 值域的子集,
则 ,解得 ,
所以实数a的取值范围为 .
同课章节目录
