苏科版九年级数学下册 8.4-8.6 抽签方法合理吗、概率帮你做估计、收取多少保费才合理 试题(含详解)
文档属性
| 名称 | 苏科版九年级数学下册 8.4-8.6 抽签方法合理吗、概率帮你做估计、收取多少保费才合理 试题(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 401.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-05 13:06:23 | ||
图片预览



文档简介
8.4-8.6 抽签方法合理吗、概率帮你做估计、收取多少保费才合理
一.单选题
1.甲、乙两人玩“石头,剪刀,布”的游戏,约定只玩一局,描述错误的是
A.甲,乙获胜的概率均低于0.5 B.甲,乙获胜的概率相同
C.甲,乙获胜的概率均高于0.5 D.游戏公平
2.在元旦联欢会上,3名小朋友分别站在三角形三个顶点的位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先坐到凳子上谁获胜,为使游戏公平,则凳子应放在三角形的
A.三条角平分线的交点 B.三条中线的交点
C.三条高的交点 D.三条边的垂直平分线的交点
3.下列说法正确的是
A.某彩票的中奖概率是,那么买100张彩票一定有5张中奖
B.某次试验投掷次数是500,计算机记录“钉尖向上”的次数是308,则该次试验“钉尖向上”的频率是0.616
C.当试验次数很大时,概率稳定在频率附近
D.试验得到的频率与概率不可能相等
4.随机抛掷一枚瓶盖1000次,经过统计得到“正面朝上”的次数为420次,则可以由此估计抛掷这枚瓶盖出现“反面朝上”的概率为
A.0.22 B.0.42 C.0.50 D.0.58
5.黄豆在相同条件下发芽率试验,结果如表.下面3个推断:①当时,黄豆发芽的频率是0.970,所以黄豆发芽概率为0.970;②根据表格数据,估计黄豆发芽的概率为0.95;③若时,估计黄豆发芽的粒数约为5700.其中正确的个数为
每批粒数 30 60 100 500 1000 3000 5000
发芽的粒数 28 58 97 479 957 2844 4752
发芽的频率 0.933 0.967 0.970 0.958 0.957 0.948 0.950
A.0个 B.1个 C.2个 D.3个
二.填空题
6.小兰和小青两人做游戏,有一个质量分布均匀的六面体骰子,骰子的六面分别标有1,2,3,4,5,6,如果掷出的骰子的点数是偶数,则小兰赢;如果掷出的骰子的点数是3的倍数,则小青赢,那么游戏规则对 有利.
7.小红和小明在操场做游戏,他们先在地上画了半径分别是和的同心圆,然后每人蒙上眼在一定距离外向圈内掷小石子,掷中阴影部分小红胜,否则小明胜,未掷入圈内不算或掷中两圆的边界线重掷,如果你是裁判,你认为游戏公平吗? .(填“公平”或“不公平” )
8.小明在一次用“频率估计概率”的试验中,把“共产党人拥有人格力量”中的每个汉字分别写在同一种卡片上,然后把卡片无字的面朝上,随机抽取一张,并统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能抽出的是 字.
9.三帆中学数学嘉年华期间,数学社团的同学做了估算的实验.方法如下:
(1)请全校同学随意写出两个实数、、可以相等),它们满足:,;
(2)统计收集上来的有效数据,设“以,,1为三条边长能构成锐角三角形”为事件;
(3)计算事件发生的概率,及收集的本校有效数据中事件出现的频率;
(4)利用频率估计概率的方法,估算出的值.
社团的同学们为了计算事件的概率,利用数形结合的方法,利用面积法计算了事件成立的概率.通过计算得到:若,,1三个数据能构成锐角三角形,则需满足.
如图所示建立坐标系.请写出图中满足事件的点所在的区域为 (写出序号即可);若利用全校1500份有效数据所估计的值为3.144,则全校搜集上来的1500份数据中能和“1”构成锐角三角形的数据有 份.
三.解答题
10.(1)有20名志愿者参加公益活动,其中男生有8名,女生有12名.若从这20名志愿者中随机选取1名作为联络员,求选到女生的概率;
(2)若该活动的某项工程只在甲、乙2人中选1人,他们准备以游戏的方式决定由谁参加,游戏规则如下:将4张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放在桌面,从中任取1张,不放回,再取1张,若牌面数字之和为偶数,则甲参加;否则乙参加.试问这个游戏公平吗?请用树状图或列表法说明理由.
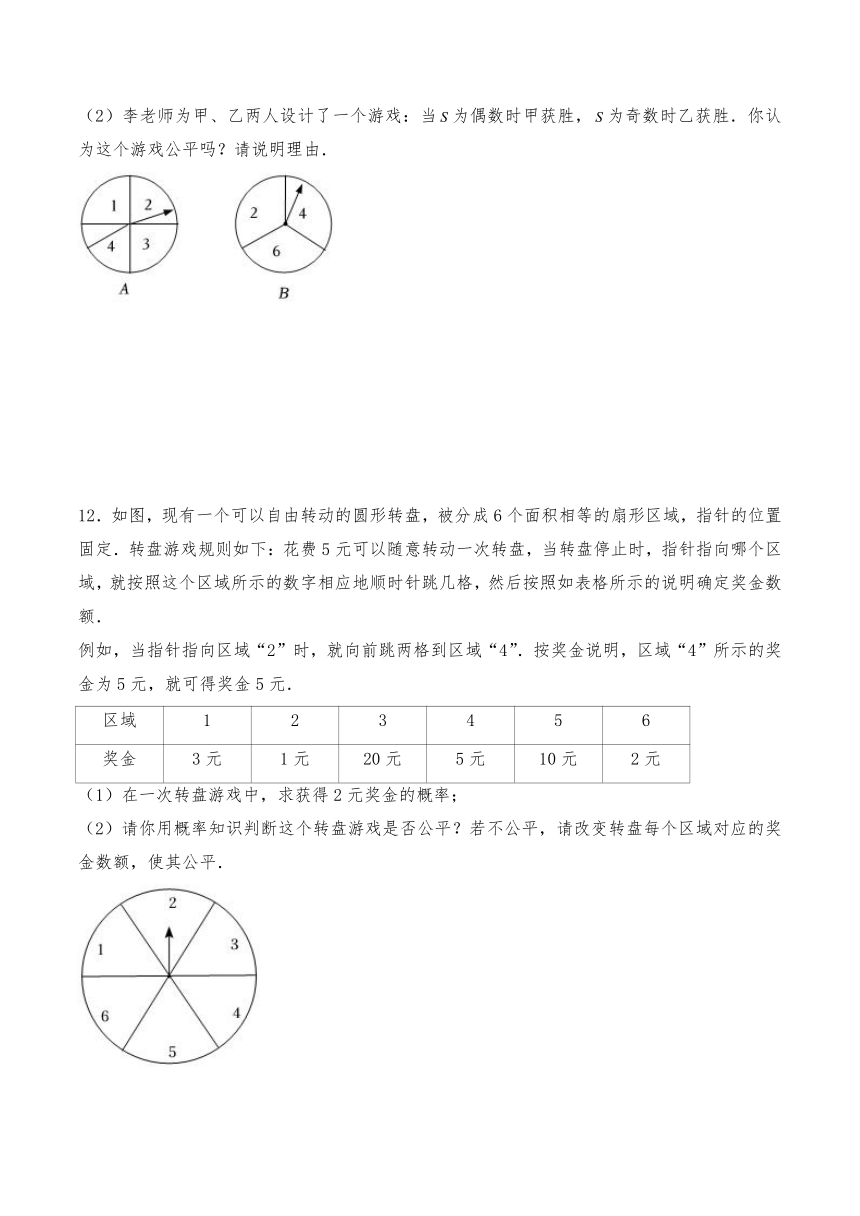
11.如图,有、两个转盘,其中转盘被分成4等份,转盘被分成3等份,并在每一份内标上数字.现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将转盘指针指向的数字记为,转盘指针指向的数字记为,从而确定点的坐标为,记.
(1)请用列表或画树状图的方法写出所有可能得到的点的坐标.
(2)李老师为甲、乙两人设计了一个游戏:当为偶数时甲获胜,为奇数时乙获胜.你认为这个游戏公平吗?请说明理由.
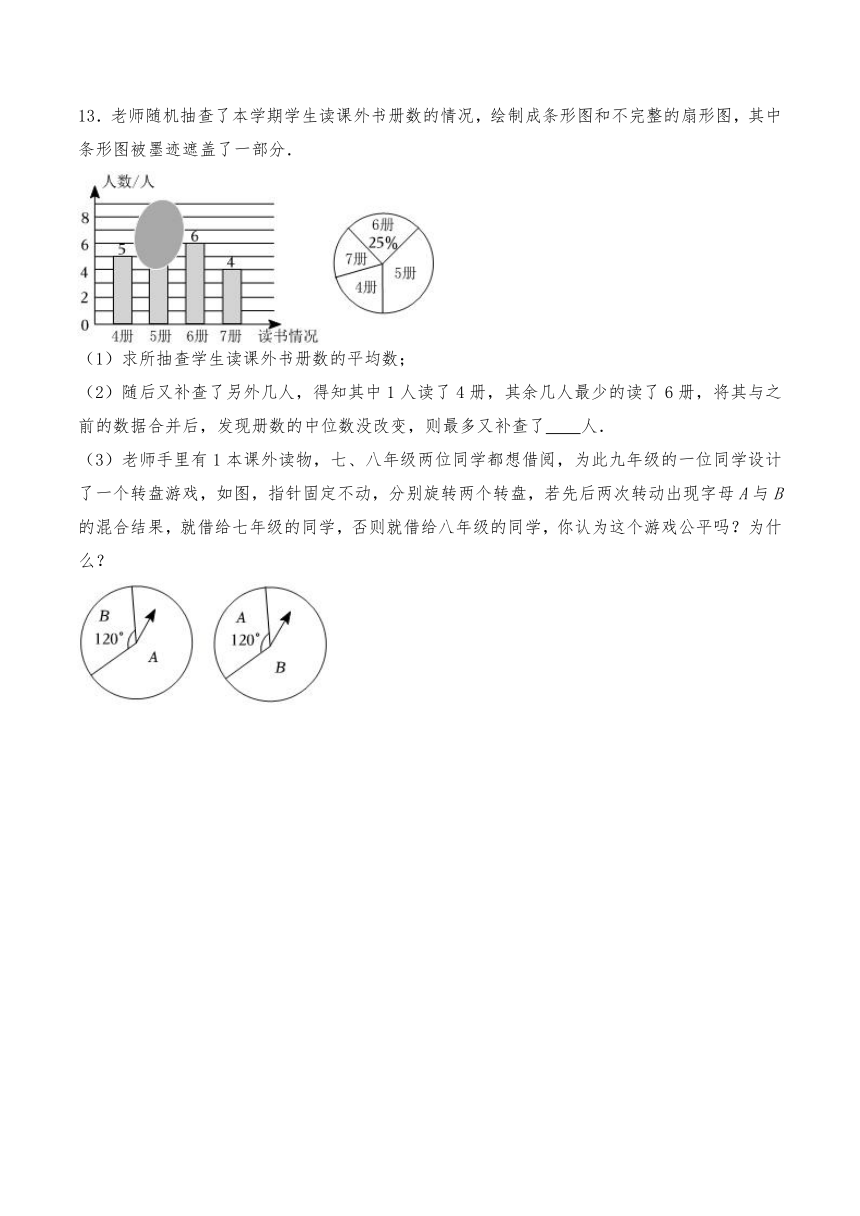
12.如图,现有一个可以自由转动的圆形转盘,被分成6个面积相等的扇形区域,指针的位置固定.转盘游戏规则如下:花费5元可以随意转动一次转盘,当转盘停止时,指针指向哪个区域,就按照这个区域所示的数字相应地顺时针跳几格,然后按照如表格所示的说明确定奖金数额.
例如,当指针指向区域“2”时,就向前跳两格到区域“4”.按奖金说明,区域“4”所示的奖金为5元,就可得奖金5元.
区域 1 2 3 4 5 6
奖金 3元 1元 20元 5元 10元 2元
(1)在一次转盘游戏中,求获得2元奖金的概率;
(2)请你用概率知识判断这个转盘游戏是否公平?若不公平,请改变转盘每个区域对应的奖金数额,使其公平.
13.老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图和不完整的扇形图,其中条形图被墨迹遮盖了一部分.
(1)求所抽查学生读课外书册数的平均数;
(2)随后又补查了另外几人,得知其中1人读了4册,其余几人最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多又补查了 人.
(3)老师手里有1本课外读物,七、八年级两位同学都想借阅,为此九年级的一位同学设计了一个转盘游戏,如图,指针固定不动,分别旋转两个转盘,若先后两次转动出现字母A与B的混合结果,就借给七年级的同学,否则就借给八年级的同学,你认为这个游戏公平吗?为什么?
14.在一个不透明的袋子里装有只有颜色不同的黑、白两种颜色的球共50个,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
摸球的次数 100 200 300 500 800 1000
摸到黑球的次数 65 118 189 310 482 602
摸到黑球的频率 0.65 0.59 0.63 0.62 0.603 0.602
(1)请估计:当很大时,摸到黑球的频率将会接近 (精确到;
(2)试估计袋子中有黑球 个;
(3)若学习小组通过试验结果,想使得在这个不透明袋子中每次摸到黑球的可能性大小为,则可以在袋子中增加相同的白球 个或减少黑球 个.
15.下表是某口罩生产厂对一批口罩质量检测的情况:
抽取口罩数 200 500 1000 1500 2000 3000
合格品数 188 471 946 1426 1898 2850
合格品频率 (精确到 0.940 0.942 0.946 0.951
(1) , ;
(2)从这批口罩中任意抽取一个是合格品的概率估计值是多少?(精确到
(3)若要生产380000个合格的口罩,该厂估计要生产多少个口罩?
16.苗木种植不仅绿了家园,助力脱贫攻坚,也成为乡村增收致富的“绿色银行”.小王承包了一片荒山,他想把这片荒山改造成一个苹果园,现在有一种苹果树苗,它的成活率如下表所示:
移植棵数 成活数 成活率 移植棵数 成活数 成活率
50 47 0.940 1500 1335 0.890
270 235 0.870 3500 3203 0.915
400 369 0.923 7000 6335
750 662 0.883 14000 12628 0.902
根据以上信息,回答下列问题:
(1)当移植的棵数是7000时,表格记录成活数是 ,那么成活率是 ;
(2)随着移植棵数的增加,树苗成活的频率总在0.900附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是 ;
(3)若小王移植10000棵这种树苗,则可能成活 ;
(4)若小王移植20000棵这种树苗,则一定成活18000棵.此结论正确吗?说明理由.
17.某航空公司的保险合同上有这样一个条款:飞机一旦失事,将向每名乘客赔偿人民币50万元,但保险公司需向每名乘客收取保险费20元.如果该航空公司航班平均每次约有120名乘客,那么平均来说,当飞机失事的概率不超过多少时,才能保证保险公司的收入不小于支出?
18.【阅读材料】一般地,如果随机事件发生的概率是(A),那么相同条件下重复次试验,事件发生的次数的平均值为(A).
假设某航班平均每次约有100名乘客,飞机失事的概率.一家保险公司要为乘客保险.承诺飞机一旦失事,将向每名乘客赔偿人民币40万元.平均来说,保险公司应该如何收取保险费呢?
设该保险公司向每名乘客收取保险费元,则在次飞行中共收取保险费元.保险公司必须保证收入不小于支出,可得100nx≥400000×100×np
(1)该保险公司向每名乘客收取的保险费应不低于 元.
【理解应用】
(2)如图,媛媛从家去学校,选择骑电瓶车,需要经过两个红绿灯路口,设每个路口可直接通过和需要等待的概率相同.
①求媛媛从家去学校在、两个路口都需要等待的概率是多少?(用列表或画树状图的方法求解)
②若,每段路平均用时均为6分钟,各路口平均需要等待时间均为1分钟,全程需要等待时间的平均值为:(A)分钟,则媛媛从家到学校所用时间的平均值为 分钟.
【拓展升华】
(3)徐老师开车去学校的道路要途径5个红绿灯路口,每个路口需要等待的概率为,直接通行的概率为,各路口平均需要等待时间均为1分钟,从家到第一个路口和最后一个路口到学校所用行驶时间均为5分钟,其余相邻两个路口间所需行驶时间均为2分钟,则徐老师从家到学校所用时间的平均值为 分钟.
19.交强险是车主必须为机动车购买的险种.若普通6座以下私家车投交强险第一年的费用(基准保费)统一为元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
交强险浮动因素和浮动费率比率表
浮动因素 浮动比率
上一个年度未发生有责任道路交通事故 下浮
上两个年度未发生有责任道路交通事故 下浮
上三个及以上年度未发生有责任道路交通事故 下浮
上一个年度发生一次有责任不涉及死亡的道路交通事故
上一个年度发生两次及两次以上有责任道路交通事故 上浮
上一个年度发生有责任道路交通死亡事故 上浮
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了80辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了如表表格:
类型
数量 20 10 10 20 15 5
以这80辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定.求某同学家里有一辆该品牌车在第四年续保时的平均费用;(费用值保留到个位数字)
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元;
①若该销售商购进两辆(车龄已满三年)该品牌二手车,第一辆经鉴定为非事故车,求第二辆车是事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的平均数.
答案
一.单选题
1.
【详解】解:由题意,列表如下:
石 剪 布
石 (石,石) (石,剪) (石,布)
剪 (剪,石) (剪,剪) (剪,布)
布 (布,石) (布,剪) (布,布)
由表格可知,共有9种等可能的结果,其中甲获胜的有3种结果,乙获胜的有3种结果,
所以甲获胜的概率乙获胜的概率.
故本题选:.
2.
【详解】解:由题意可得,
3个小朋友到板凳的距离相等游戏才是公平的,
于是板凳的位置到三角形3个顶点的距离相等,
因此板凳的位置是三角形三边的垂直平分线的交点.
故本题选:.
3.
【详解】解:.某彩票的中奖概率是,那么买100张彩票可能有5张中奖,此选项说法错误;
.某次试验投掷次数是500,计算机记录“钉尖向上”的次数是308,则该次试验“钉尖向上”的频率是0.616,此选项说法正确;
.当试验次数很大时,频率稳定在概率附近,此选项说法错误;
.试验得到的频率与概率可能相等,此选项说法错误.
故本题选:.
4.
【详解】解:随机抛掷一枚瓶盖1000次,经过统计得到“正面朝上”的次数为420次,
所以由此估计抛掷这枚瓶盖出现“反面朝上”的概率为.
故本题选:.
5.
【详解】解:①当时,黄豆发芽的频率是0.970,所以黄豆发芽概率为0.970;此推断错误;
②根据表格数据,估计黄豆发芽的概率为0.95;此推断正确;
③若时,估计黄豆发芽的粒数约为.此结论正确.
故本题选:.
二.填空题
6.
【详解】解:骰子的点数是偶数的有2,4,6,其概率为,
骰子的点数是3的倍数的有3,6,其概率为,
游戏规则对小兰有利.
故本题答案为:不公平.
7.
【详解】解:内圆的面积为:,外圆的面积为,
小明胜的概率为,
环形的面积为:,
小红胜的概率为,
,
这个游戏不公平.
故本题答案为:不公平.
8.
【详解】解:由折线统计图知,该字出现的频率稳定在数字附近,
所以该字出现的概率约为,
而“共产党人拥有人格力量”一共有10个字,
所以该字的个数为,
符合这一结果的试验最有可能抽出的是人字.
故本题答案为:人.
9.
【详解】解:全校同学随意写出两个实数、、可以相等),它们满足:,,
可用图形中的正方形区域表示,以,,1为三条边长能构成锐角三角形需满足,,可用图中的(3)区域表示,
设“以,,1为三条边长能构成锐角三角形”为事件,
由几何概型的公式可知,(A),
全校1500份有效数据所估计的值为3.144,
(A),
全校搜集上来的1500份数据中能和“1”构成锐角三角形的数据有(A)(份.
故本题答案为:(3),321.
三.解答题
10.解:(1);
(2)画树状图如下:
共有12种等可能的情况,和为偶数的情况有4种,奇数的情况有8种,
,,
,
不公平.
11.解:(1)列表如下,
1 2 3 4
2
4
6
所有可能出现的结果共有12种,它们出现的可能性都相同;
(2)这个游戏公平,理由如下:
可能出现的结果有3、5、7、4、6、8、5、7、9、6、8、10共12种,其中偶数有6个,奇数有6个,
,
即,
这个游戏是公平的.
12.解:(1)列表如下:
指针指向的数字 最后跳到的数字 奖金数额
1 2 1元
2 4 5元
3 6 2元
4 2 1元
5 4 5元
6 6 2元
共有6种等可能的结果,因此获得2元奖金的概率为;
(2)转一次转盘的平均收益为:(元,
又,
这个转盘游戏对游戏者不公平,
更改转盘每个区域对应的奖金数额如下表:
区域 1 2 3 4 5 6
奖金 3元 3元 20元 8元 10元 4元
13.解:(1)抽查的总人数为:6÷0.25=24(人),
∴读5册的学生有:24﹣5﹣6﹣4=9(人),
∴所抽查学生读课外书册数的平均数为:×(4×5+5×9+6×6+4×7)=5.375(本);
(2)原来的中位数为:5,
6+9=15﹣10=4,4+1=5,
故本题答案为:5;
(3)不公平,理由如下:
借给七年级同学的概率为:,
借给八年级同学的概率为:1﹣=,
∵≠,
故游戏不公平.
14.解:(1)观察表格得:当很大时,摸到黑球的频率将会接近0.6,
故本题答案为:0.6;
(2)黑球的个数为个,
故本题答案为:30;
(3)想使得在这个不透明袋子中每次摸到黑球的可能性大小为,则可以使得黑球和白球的个数相同,即在袋子中增加相同的白球10个或减少黑球10个,
故本题答案为:10,10.
15.
【详解】解:(1),,
故本题答案为:0.949,0.950;
(2)由表格可知,随着抽取的口罩数量不断增大,任意抽取一个是合格的频率在0.95附近波动,
所以任意抽取的一个是合格品的概率估计值是0.95;
(3),
答:该厂估计要生产400000个口罩.
16.解:(1)当移植的树数是7000时,表格记录成活数是6335,那么成活率是0.905,
故本题答案为:6335,0.905;
(2)随着移植棵数的增加,树苗成活的频率总在0.900附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是0.900,
故本题答案为:0.900;
(3)若小张移植10000棵这种树苗,则可能成活(棵,
故本题答案为:9000棵;
(4)此结论错误,理由如下:
随着移植棵数的增加,树苗成活的频率总在0.900附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是0.900,
成活的概率是0.900可能发生,也可能不发生,
故若小张移植20000棵这种树苗,不一定成活18000棵.
17.解:收取保险费(元,
每次约有120名乘客,如飞机一旦失事,每位乘客赔偿50万人民币,共计6000万元,
一次飞行中飞机失事的概率不超过,
答:当飞机失事的概率不超过0.00004时,才能保证保险公司的收入不小于支出.
18.解:(1)100nx≥400000×100×0.00005n,解得:x≥20,
的最小值是20,
故本题答案为:20;
(2)①树状图如图示:
在、两个路口都需等待的概率是;
②由题意得:;
(3)全程需要等待时间的平均值为:(A),
徐老师从家到学校所用时间的平均值为:.
19.解:(1)根据题意可知,的取值可能为,,,,,,
由统计数据可知对应的概率为:,,,,,.
平均费用为:(元,
第四年续保时的平均费用是903元;
(2)①由统计数据可知任意一辆该品牌车龄已满三年的二手车为非事故车的概率为,第二辆车是事故车的概率:;
②设为该销售商购进并销售一辆二手车的利润,则的可能取值为,10000.
一辆汽车的平均利润为:,
该销售商一次购进100辆该品牌车龄已满三年的二手车获得利润的平均数为(万元).
一.单选题
1.甲、乙两人玩“石头,剪刀,布”的游戏,约定只玩一局,描述错误的是
A.甲,乙获胜的概率均低于0.5 B.甲,乙获胜的概率相同
C.甲,乙获胜的概率均高于0.5 D.游戏公平
2.在元旦联欢会上,3名小朋友分别站在三角形三个顶点的位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先坐到凳子上谁获胜,为使游戏公平,则凳子应放在三角形的
A.三条角平分线的交点 B.三条中线的交点
C.三条高的交点 D.三条边的垂直平分线的交点
3.下列说法正确的是
A.某彩票的中奖概率是,那么买100张彩票一定有5张中奖
B.某次试验投掷次数是500,计算机记录“钉尖向上”的次数是308,则该次试验“钉尖向上”的频率是0.616
C.当试验次数很大时,概率稳定在频率附近
D.试验得到的频率与概率不可能相等
4.随机抛掷一枚瓶盖1000次,经过统计得到“正面朝上”的次数为420次,则可以由此估计抛掷这枚瓶盖出现“反面朝上”的概率为
A.0.22 B.0.42 C.0.50 D.0.58
5.黄豆在相同条件下发芽率试验,结果如表.下面3个推断:①当时,黄豆发芽的频率是0.970,所以黄豆发芽概率为0.970;②根据表格数据,估计黄豆发芽的概率为0.95;③若时,估计黄豆发芽的粒数约为5700.其中正确的个数为
每批粒数 30 60 100 500 1000 3000 5000
发芽的粒数 28 58 97 479 957 2844 4752
发芽的频率 0.933 0.967 0.970 0.958 0.957 0.948 0.950
A.0个 B.1个 C.2个 D.3个
二.填空题
6.小兰和小青两人做游戏,有一个质量分布均匀的六面体骰子,骰子的六面分别标有1,2,3,4,5,6,如果掷出的骰子的点数是偶数,则小兰赢;如果掷出的骰子的点数是3的倍数,则小青赢,那么游戏规则对 有利.
7.小红和小明在操场做游戏,他们先在地上画了半径分别是和的同心圆,然后每人蒙上眼在一定距离外向圈内掷小石子,掷中阴影部分小红胜,否则小明胜,未掷入圈内不算或掷中两圆的边界线重掷,如果你是裁判,你认为游戏公平吗? .(填“公平”或“不公平” )
8.小明在一次用“频率估计概率”的试验中,把“共产党人拥有人格力量”中的每个汉字分别写在同一种卡片上,然后把卡片无字的面朝上,随机抽取一张,并统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能抽出的是 字.
9.三帆中学数学嘉年华期间,数学社团的同学做了估算的实验.方法如下:
(1)请全校同学随意写出两个实数、、可以相等),它们满足:,;
(2)统计收集上来的有效数据,设“以,,1为三条边长能构成锐角三角形”为事件;
(3)计算事件发生的概率,及收集的本校有效数据中事件出现的频率;
(4)利用频率估计概率的方法,估算出的值.
社团的同学们为了计算事件的概率,利用数形结合的方法,利用面积法计算了事件成立的概率.通过计算得到:若,,1三个数据能构成锐角三角形,则需满足.
如图所示建立坐标系.请写出图中满足事件的点所在的区域为 (写出序号即可);若利用全校1500份有效数据所估计的值为3.144,则全校搜集上来的1500份数据中能和“1”构成锐角三角形的数据有 份.
三.解答题
10.(1)有20名志愿者参加公益活动,其中男生有8名,女生有12名.若从这20名志愿者中随机选取1名作为联络员,求选到女生的概率;
(2)若该活动的某项工程只在甲、乙2人中选1人,他们准备以游戏的方式决定由谁参加,游戏规则如下:将4张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放在桌面,从中任取1张,不放回,再取1张,若牌面数字之和为偶数,则甲参加;否则乙参加.试问这个游戏公平吗?请用树状图或列表法说明理由.
11.如图,有、两个转盘,其中转盘被分成4等份,转盘被分成3等份,并在每一份内标上数字.现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将转盘指针指向的数字记为,转盘指针指向的数字记为,从而确定点的坐标为,记.
(1)请用列表或画树状图的方法写出所有可能得到的点的坐标.
(2)李老师为甲、乙两人设计了一个游戏:当为偶数时甲获胜,为奇数时乙获胜.你认为这个游戏公平吗?请说明理由.
12.如图,现有一个可以自由转动的圆形转盘,被分成6个面积相等的扇形区域,指针的位置固定.转盘游戏规则如下:花费5元可以随意转动一次转盘,当转盘停止时,指针指向哪个区域,就按照这个区域所示的数字相应地顺时针跳几格,然后按照如表格所示的说明确定奖金数额.
例如,当指针指向区域“2”时,就向前跳两格到区域“4”.按奖金说明,区域“4”所示的奖金为5元,就可得奖金5元.
区域 1 2 3 4 5 6
奖金 3元 1元 20元 5元 10元 2元
(1)在一次转盘游戏中,求获得2元奖金的概率;
(2)请你用概率知识判断这个转盘游戏是否公平?若不公平,请改变转盘每个区域对应的奖金数额,使其公平.
13.老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图和不完整的扇形图,其中条形图被墨迹遮盖了一部分.
(1)求所抽查学生读课外书册数的平均数;
(2)随后又补查了另外几人,得知其中1人读了4册,其余几人最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多又补查了 人.
(3)老师手里有1本课外读物,七、八年级两位同学都想借阅,为此九年级的一位同学设计了一个转盘游戏,如图,指针固定不动,分别旋转两个转盘,若先后两次转动出现字母A与B的混合结果,就借给七年级的同学,否则就借给八年级的同学,你认为这个游戏公平吗?为什么?
14.在一个不透明的袋子里装有只有颜色不同的黑、白两种颜色的球共50个,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
摸球的次数 100 200 300 500 800 1000
摸到黑球的次数 65 118 189 310 482 602
摸到黑球的频率 0.65 0.59 0.63 0.62 0.603 0.602
(1)请估计:当很大时,摸到黑球的频率将会接近 (精确到;
(2)试估计袋子中有黑球 个;
(3)若学习小组通过试验结果,想使得在这个不透明袋子中每次摸到黑球的可能性大小为,则可以在袋子中增加相同的白球 个或减少黑球 个.
15.下表是某口罩生产厂对一批口罩质量检测的情况:
抽取口罩数 200 500 1000 1500 2000 3000
合格品数 188 471 946 1426 1898 2850
合格品频率 (精确到 0.940 0.942 0.946 0.951
(1) , ;
(2)从这批口罩中任意抽取一个是合格品的概率估计值是多少?(精确到
(3)若要生产380000个合格的口罩,该厂估计要生产多少个口罩?
16.苗木种植不仅绿了家园,助力脱贫攻坚,也成为乡村增收致富的“绿色银行”.小王承包了一片荒山,他想把这片荒山改造成一个苹果园,现在有一种苹果树苗,它的成活率如下表所示:
移植棵数 成活数 成活率 移植棵数 成活数 成活率
50 47 0.940 1500 1335 0.890
270 235 0.870 3500 3203 0.915
400 369 0.923 7000 6335
750 662 0.883 14000 12628 0.902
根据以上信息,回答下列问题:
(1)当移植的棵数是7000时,表格记录成活数是 ,那么成活率是 ;
(2)随着移植棵数的增加,树苗成活的频率总在0.900附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是 ;
(3)若小王移植10000棵这种树苗,则可能成活 ;
(4)若小王移植20000棵这种树苗,则一定成活18000棵.此结论正确吗?说明理由.
17.某航空公司的保险合同上有这样一个条款:飞机一旦失事,将向每名乘客赔偿人民币50万元,但保险公司需向每名乘客收取保险费20元.如果该航空公司航班平均每次约有120名乘客,那么平均来说,当飞机失事的概率不超过多少时,才能保证保险公司的收入不小于支出?
18.【阅读材料】一般地,如果随机事件发生的概率是(A),那么相同条件下重复次试验,事件发生的次数的平均值为(A).
假设某航班平均每次约有100名乘客,飞机失事的概率.一家保险公司要为乘客保险.承诺飞机一旦失事,将向每名乘客赔偿人民币40万元.平均来说,保险公司应该如何收取保险费呢?
设该保险公司向每名乘客收取保险费元,则在次飞行中共收取保险费元.保险公司必须保证收入不小于支出,可得100nx≥400000×100×np
(1)该保险公司向每名乘客收取的保险费应不低于 元.
【理解应用】
(2)如图,媛媛从家去学校,选择骑电瓶车,需要经过两个红绿灯路口,设每个路口可直接通过和需要等待的概率相同.
①求媛媛从家去学校在、两个路口都需要等待的概率是多少?(用列表或画树状图的方法求解)
②若,每段路平均用时均为6分钟,各路口平均需要等待时间均为1分钟,全程需要等待时间的平均值为:(A)分钟,则媛媛从家到学校所用时间的平均值为 分钟.
【拓展升华】
(3)徐老师开车去学校的道路要途径5个红绿灯路口,每个路口需要等待的概率为,直接通行的概率为,各路口平均需要等待时间均为1分钟,从家到第一个路口和最后一个路口到学校所用行驶时间均为5分钟,其余相邻两个路口间所需行驶时间均为2分钟,则徐老师从家到学校所用时间的平均值为 分钟.
19.交强险是车主必须为机动车购买的险种.若普通6座以下私家车投交强险第一年的费用(基准保费)统一为元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
交强险浮动因素和浮动费率比率表
浮动因素 浮动比率
上一个年度未发生有责任道路交通事故 下浮
上两个年度未发生有责任道路交通事故 下浮
上三个及以上年度未发生有责任道路交通事故 下浮
上一个年度发生一次有责任不涉及死亡的道路交通事故
上一个年度发生两次及两次以上有责任道路交通事故 上浮
上一个年度发生有责任道路交通死亡事故 上浮
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了80辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了如表表格:
类型
数量 20 10 10 20 15 5
以这80辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定.求某同学家里有一辆该品牌车在第四年续保时的平均费用;(费用值保留到个位数字)
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元;
①若该销售商购进两辆(车龄已满三年)该品牌二手车,第一辆经鉴定为非事故车,求第二辆车是事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的平均数.
答案
一.单选题
1.
【详解】解:由题意,列表如下:
石 剪 布
石 (石,石) (石,剪) (石,布)
剪 (剪,石) (剪,剪) (剪,布)
布 (布,石) (布,剪) (布,布)
由表格可知,共有9种等可能的结果,其中甲获胜的有3种结果,乙获胜的有3种结果,
所以甲获胜的概率乙获胜的概率.
故本题选:.
2.
【详解】解:由题意可得,
3个小朋友到板凳的距离相等游戏才是公平的,
于是板凳的位置到三角形3个顶点的距离相等,
因此板凳的位置是三角形三边的垂直平分线的交点.
故本题选:.
3.
【详解】解:.某彩票的中奖概率是,那么买100张彩票可能有5张中奖,此选项说法错误;
.某次试验投掷次数是500,计算机记录“钉尖向上”的次数是308,则该次试验“钉尖向上”的频率是0.616,此选项说法正确;
.当试验次数很大时,频率稳定在概率附近,此选项说法错误;
.试验得到的频率与概率可能相等,此选项说法错误.
故本题选:.
4.
【详解】解:随机抛掷一枚瓶盖1000次,经过统计得到“正面朝上”的次数为420次,
所以由此估计抛掷这枚瓶盖出现“反面朝上”的概率为.
故本题选:.
5.
【详解】解:①当时,黄豆发芽的频率是0.970,所以黄豆发芽概率为0.970;此推断错误;
②根据表格数据,估计黄豆发芽的概率为0.95;此推断正确;
③若时,估计黄豆发芽的粒数约为.此结论正确.
故本题选:.
二.填空题
6.
【详解】解:骰子的点数是偶数的有2,4,6,其概率为,
骰子的点数是3的倍数的有3,6,其概率为,
游戏规则对小兰有利.
故本题答案为:不公平.
7.
【详解】解:内圆的面积为:,外圆的面积为,
小明胜的概率为,
环形的面积为:,
小红胜的概率为,
,
这个游戏不公平.
故本题答案为:不公平.
8.
【详解】解:由折线统计图知,该字出现的频率稳定在数字附近,
所以该字出现的概率约为,
而“共产党人拥有人格力量”一共有10个字,
所以该字的个数为,
符合这一结果的试验最有可能抽出的是人字.
故本题答案为:人.
9.
【详解】解:全校同学随意写出两个实数、、可以相等),它们满足:,,
可用图形中的正方形区域表示,以,,1为三条边长能构成锐角三角形需满足,,可用图中的(3)区域表示,
设“以,,1为三条边长能构成锐角三角形”为事件,
由几何概型的公式可知,(A),
全校1500份有效数据所估计的值为3.144,
(A),
全校搜集上来的1500份数据中能和“1”构成锐角三角形的数据有(A)(份.
故本题答案为:(3),321.
三.解答题
10.解:(1);
(2)画树状图如下:
共有12种等可能的情况,和为偶数的情况有4种,奇数的情况有8种,
,,
,
不公平.
11.解:(1)列表如下,
1 2 3 4
2
4
6
所有可能出现的结果共有12种,它们出现的可能性都相同;
(2)这个游戏公平,理由如下:
可能出现的结果有3、5、7、4、6、8、5、7、9、6、8、10共12种,其中偶数有6个,奇数有6个,
,
即,
这个游戏是公平的.
12.解:(1)列表如下:
指针指向的数字 最后跳到的数字 奖金数额
1 2 1元
2 4 5元
3 6 2元
4 2 1元
5 4 5元
6 6 2元
共有6种等可能的结果,因此获得2元奖金的概率为;
(2)转一次转盘的平均收益为:(元,
又,
这个转盘游戏对游戏者不公平,
更改转盘每个区域对应的奖金数额如下表:
区域 1 2 3 4 5 6
奖金 3元 3元 20元 8元 10元 4元
13.解:(1)抽查的总人数为:6÷0.25=24(人),
∴读5册的学生有:24﹣5﹣6﹣4=9(人),
∴所抽查学生读课外书册数的平均数为:×(4×5+5×9+6×6+4×7)=5.375(本);
(2)原来的中位数为:5,
6+9=15﹣10=4,4+1=5,
故本题答案为:5;
(3)不公平,理由如下:
借给七年级同学的概率为:,
借给八年级同学的概率为:1﹣=,
∵≠,
故游戏不公平.
14.解:(1)观察表格得:当很大时,摸到黑球的频率将会接近0.6,
故本题答案为:0.6;
(2)黑球的个数为个,
故本题答案为:30;
(3)想使得在这个不透明袋子中每次摸到黑球的可能性大小为,则可以使得黑球和白球的个数相同,即在袋子中增加相同的白球10个或减少黑球10个,
故本题答案为:10,10.
15.
【详解】解:(1),,
故本题答案为:0.949,0.950;
(2)由表格可知,随着抽取的口罩数量不断增大,任意抽取一个是合格的频率在0.95附近波动,
所以任意抽取的一个是合格品的概率估计值是0.95;
(3),
答:该厂估计要生产400000个口罩.
16.解:(1)当移植的树数是7000时,表格记录成活数是6335,那么成活率是0.905,
故本题答案为:6335,0.905;
(2)随着移植棵数的增加,树苗成活的频率总在0.900附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是0.900,
故本题答案为:0.900;
(3)若小张移植10000棵这种树苗,则可能成活(棵,
故本题答案为:9000棵;
(4)此结论错误,理由如下:
随着移植棵数的增加,树苗成活的频率总在0.900附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是0.900,
成活的概率是0.900可能发生,也可能不发生,
故若小张移植20000棵这种树苗,不一定成活18000棵.
17.解:收取保险费(元,
每次约有120名乘客,如飞机一旦失事,每位乘客赔偿50万人民币,共计6000万元,
一次飞行中飞机失事的概率不超过,
答:当飞机失事的概率不超过0.00004时,才能保证保险公司的收入不小于支出.
18.解:(1)100nx≥400000×100×0.00005n,解得:x≥20,
的最小值是20,
故本题答案为:20;
(2)①树状图如图示:
在、两个路口都需等待的概率是;
②由题意得:;
(3)全程需要等待时间的平均值为:(A),
徐老师从家到学校所用时间的平均值为:.
19.解:(1)根据题意可知,的取值可能为,,,,,,
由统计数据可知对应的概率为:,,,,,.
平均费用为:(元,
第四年续保时的平均费用是903元;
(2)①由统计数据可知任意一辆该品牌车龄已满三年的二手车为非事故车的概率为,第二辆车是事故车的概率:;
②设为该销售商购进并销售一辆二手车的利润,则的可能取值为,10000.
一辆汽车的平均利润为:,
该销售商一次购进100辆该品牌车龄已满三年的二手车获得利润的平均数为(万元).
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
