小升初分班考综合检测卷(含答案)数学六年级下册苏教版江苏地区适用
文档属性
| 名称 | 小升初分班考综合检测卷(含答案)数学六年级下册苏教版江苏地区适用 |  | |
| 格式 | docx | ||
| 文件大小 | 600.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-05 09:15:46 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
绝密★启用前
小升初分班考综合检测卷-数学六年级下册苏教版江苏地区适用
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
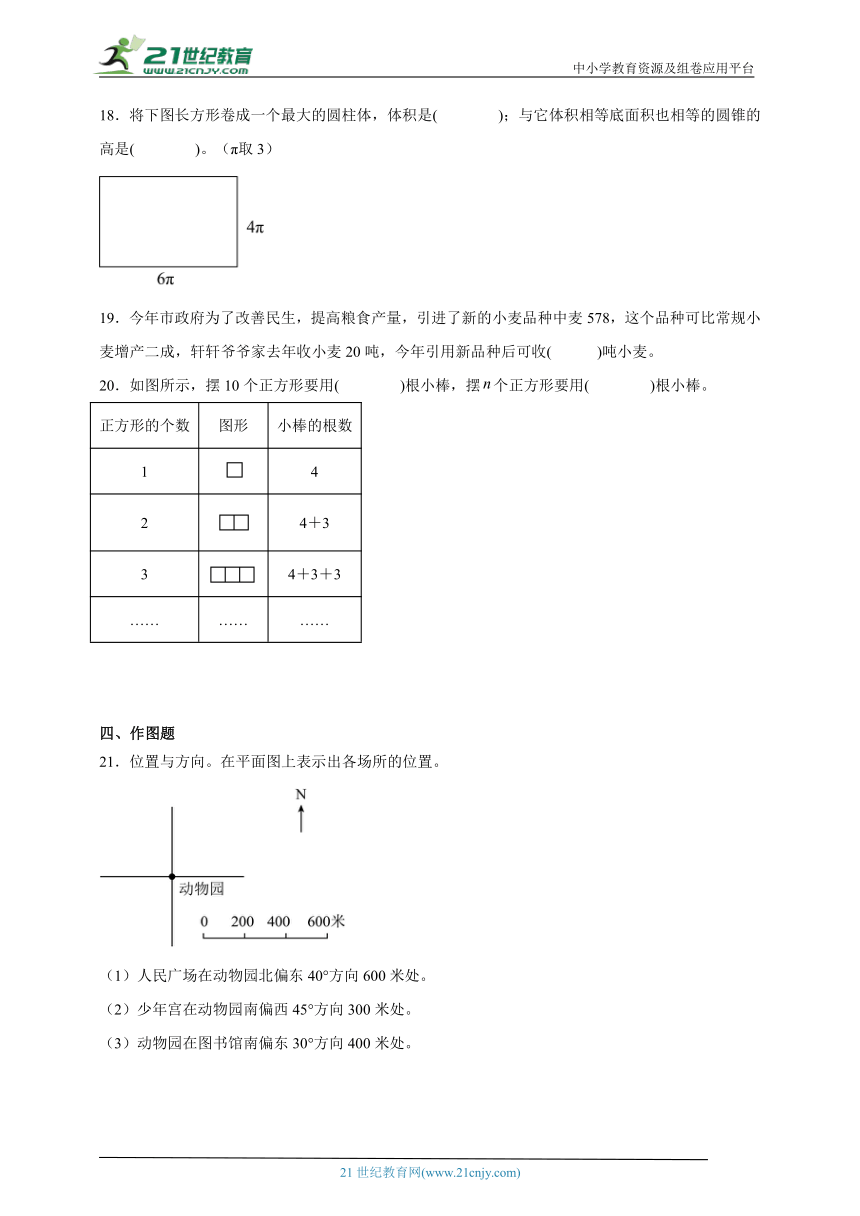
一、计算题
1.直接写得数。
10-9.94= 2.7×4×0.25= 30×30%=
2.用递等式计算,能简算的简算。
(1)3750÷(25+25×2) (2)×+80%÷
(3)5.75-(+) (4)+(0.75+0.25÷)
3.解方程或比例。
4.计算下图中阴影部分的面积。
二、选择题
5.妙想做抛硬币游戏(硬币是均匀的),前三次抛硬币的结果都是正面朝下,第四次正面朝上的可能性是( )。
A.0 B. C. D.1
6.算式1.2×3.2的积与两个因数比,( )。
A.比两个因数都大 B.比两个因数都小 C.与其中一个因数相等 D.无法确定
7.下图中有大小两个正方形,已知阴影部分的面积是5cm2,则圆环的面积是( )cm2。
A.6.28 B.15.7 C.18.84 D.28.26
8.甲乙的比为,甲数比乙数多______,乙数又比甲数少______,选项为( )。
A., B., C., D.,
9.下图表示两辆汽车所行驶的路程与相应时间关系的图象。下列关于图象描述错误的是( )。
A.两辆汽车行驶的路程和时间都是成正比例关系
B.从昆明到大理大约有350千米,①号车大约要4小时能到大理
C.从图象上看,①号车的速度比②号车快
D.从图象上看,②号车的速度比①号车快
10.一根长方体木料,长2米,宽和厚都是5米,把它锯成1米长的两段,表面积增加了( )平方米。
A.50 B.40 C.45 D.25
11.一个圆柱和一个圆锥的底面半径的比是3∶4,高度的比是2∶3,圆柱与圆锥的体积比( )。
A.1∶2 B.3∶2 C.9∶8 D.3∶8
12.小南统计学校五、六年级的男生和女生人数,制成了下面扇形统计图. 请你根据图中反映的男生女生人数的关系判断,下面说法可能正确的是( )
A.五年级160人,六年级200人 B.五年级200人,六年级225人
C.五年级200人,六年级160人 D.五年级250人,六年级200人
三、填空题
13.一个九位数,最高位是4,千万位和千位都是7,其他各个数位上都是0,这个数是( )。省略亿位后面的尾数约是( )亿。
14.三角形的面积是3.5平方米,与它等底等高的平行四边形的面积是( )平方米。
15.篮球兴趣小组有47人,至少有( )人的属相是相同的。
16.如果一辆汽车平均每天节约汽油升,6天可节约汽油( )升。
17.某学校教学楼的长为66米,宽12米,把它画在比例尺是1∶300的学校平面图上,教学楼的宽在图上距离是( )厘米。
18.将下图长方形卷成一个最大的圆柱体,体积是( );与它体积相等底面积也相等的圆锥的高是( )。(π取3)
19.今年市政府为了改善民生,提高粮食产量,引进了新的小麦品种中麦578,这个品种可比常规小麦增产二成,轩轩爷爷家去年收小麦20吨,今年引用新品种后可收( )吨小麦。
20.如图所示,摆10个正方形要用( )根小棒,摆个正方形要用( )根小棒。
正方形的个数 图形 小棒的根数
1 4
2 4+3
3 4+3+3
…… …… ……
四、作图题
21.位置与方向。在平面图上表示出各场所的位置。
(1)人民广场在动物园北偏东40°方向600米处。
(2)少年宫在动物园南偏西45°方向300米处。
(3)动物园在图书馆南偏东30°方向400米处。
五、解答题
22.在这学期的读书月活动中,丽丽共借阅了48本课外书籍。丽丽借书的本数的正好是强强的本数。强强借了多少本课外书籍?
23.高度适宜的书桌对孩子养成良好的体姿很重要。科学研究发现,学生身高大约比书桌高度的3倍少0.4米时最适合学生良好体姿的形成。照此推算,身高为1.55米的学生,所用书桌的高度应是多少米?(用方程解)
24.元旦节搞促销,两种品牌的饮水机各卖一台,售价都是600元,一台赚了20%,另一台亏20%,请你算一算这两台饮水机赚了还是亏了?赚(或亏)了多少元?
25.图书馆新购进了840本新书,其中的借给了四年级,剩下的书按5∶4借给五、六年级,六年级借到了多少本新书?
26.现有两个等高的容器(如图),圆锥体容器的半径是15厘米,圆柱体容器的半径是12厘米。现将圆锥体容器装满水倒入圆柱体容器内,这时水深比圆柱体容器高度的低3厘米。问:这两个容器的高是多少厘米?
27.下面是万家乐超市甲、乙两个分店去年四个季度的销售额统计图,请你看图回答问题。
(1)甲、乙两个分店平均每个季度的销售额各是多少万元?
(2)说说两个店销售额的变化情况,说说你还能找到哪些数学信息?(只要写一条就可以)
参考答案:
1.;0.06;2.7;9
2;;;
【详解】略
2.225;;4;
【分析】(1)可运用除法的性质将3750÷(25+25×2)转化为3750÷25+3750÷50,进行简便计算。
(2)将×+80%÷转化为×+×即可运用乘法分配律进行简算。
(3)5.75=5;所以原式=5--,由此进行简算。
(4)原式=+(+×),先计算括号里的乘法,再计算加法,最后计算括号外的加法。
【详解】(1)3750÷(25+25×2)
=3750÷25+3750÷50
=150+75
=225
(2)×+80%÷
=×+×
=×(+)
=×1
=
(3)5.75-(+)
=5--
=5-
=4
(4)+(0.75+0.25÷)
=+(+×)
=+(+)
=+()
=
=
【点睛】本题考查了数的简便计算;关键是要结合题意灵活运用运算律进行简算。
3.;;
【分析】,先将左边合并成,根据等式的性质2,两边同时÷即可;
,根据等式的性质1和2,两边同时+3×0.7的积,再同时÷4即可;
,根据比例的基本性质,先写成的形式,两边同时÷0.7即可。
【详解】
解:
解:
解:
4.86平方厘米
【分析】观察图形可知,阴影部分的面积=正方形的面积-圆的面积,根据正方形、圆的面积计算公式进行计算即可。
【详解】20×20-3.14×202×
=20×20-3.14×400×
=20×20-1256×
=400-314
=86(平方厘米)
所以,阴影部分的面积是86平方厘米。
5.B
【分析】硬币有正反两个面,每次抛硬币,正面和反面朝上的可能性都一样,根据分数的意义,确定正面朝上的可能性即可。
【详解】因为硬币有正反两个面,无论前三次抛硬币是什么结果,第四次正面朝上的可能性是。
故答案为:B
【点睛】只有在每个结果发生的可能性都相等的条件下才能表示出其发生的可能性。
6.A
【分析】一个数(0除外),乘大于1的数,积比原数大,据此分析。
【详解】1.2>1,3.2>1,1.2×3.2>1.2,1.2×3.2>3.2,算式1.2×3.2的积与两个因数比,比两个因数都大。
故答案为:A
【点睛】关键是掌握小数乘法的计算方法。
7.B
【分析】从图意可知,大正方形的边长=大圆半径,小正方形边长=小圆半径,阴影部分的面积=大正方形的面积-小正方形的面积=R2-r2=5cm2。圆环的面积:S=πR2-πr2=π(R2-r2)。所以用5×3.14即可求出圆环的面积。据此解答。
【详解】根据分析可得:
5×3.14=15.7(cm2)
圆环的面积是15.7 cm2。
故答案为:B
【点睛】理解大小正方形的面积差就是大小圆的半径平方差,是解题的关键。
8.B
【分析】根据“甲乙的比为”把甲看作5份,乙看作4份,先求出甲乙两数的差;
求甲数比乙数多百分之几,应该把乙数看作单位“1”,用两数差除以乙数;
求乙数比甲数少百分之几,应该把甲数看作单位“1”,用两数差除以甲数。
【详解】;
;
;
即甲数比乙数多,乙数比甲数少。
故答案为:B
9.D
【分析】正比例关系的图象是一条经过原点的直线;反比例关系的图象是一条不过原点的曲线;利用正比例和反比例的概念,以及统计图中的数据,逐项分析判断。
【详解】A.因为两辆汽车的图象都是一条经过原点的直线,所以两辆汽车行驶的路程和时间都是成正比例关系,原题说法正确;
B.从图象可以看出,从昆明到大理大约有350千米,①号车大约要4小时能到大理,原题说法正确;
C.从图象可以看出,①号车行360千米用时4小时,②号车行360千米用时8小时,路程相同时,时间越短,速度越快,所以①号车的速度比②号车快,原题说法正确;
D.由C可知,②号车的速度比①号车慢,原题说法错误。
故答案为:D
【点睛】掌握正比例关系的意义和图象的特征、以及折线统计图的特点和作用是解题的关键。
10.A
【分析】把它锯成1米长的两段,表面积增加了两个边长为5米的正方形面,利用正方形的面积公式,由此可以解决问题。
【详解】5×5×2
=25×2
=50(平方米)
表面积增加了50平方米。
故答案为:A
11.C
【分析】根据题意,设圆锥的底面半径为4r,则圆柱的半径为3r,设圆柱的高为2h,则圆锥的高为3h;根据圆柱的体积公式:底面积×高;圆锥的体积公式:底面积×高×,求出圆柱和圆锥的体积,再根据比的意义,用圆柱的体积∶圆锥的体积,化简即可解答。
【详解】解:设圆柱的底面半径是3r,则圆锥的底面半径是4r,设圆柱的高就是2h,则圆锥的高是3h,
那么圆柱的体积是:π×(3r)2×2h
=π×9r2×2h
=9πr2×2h
=18πr2h
圆锥的体积是:π×(4r)2×3h×
=π×16r2×3h×
=16πr2×3h×
=48πr2h×
=16πr2h
圆柱与圆锥的体积的比是:
18πr2h∶16πr2h
=18∶16
=(18÷2)∶(16÷2)
=9∶8
圆柱与圆锥的体积比是9∶8。
故答案为:C
【点睛】根据圆柱的体积公式、圆锥的体积公式以及比的意义进行解答。
12.A
【详解】五年级女生人数占全班人数:;六年级女生占全班人数;五六班女生人数占两个班总人数的
A、
B、
C、
D、
【点睛】根据扇形统计图可知:五年级女生人数所占扇形圆心角的度数为180°,也就是女生人数占全班人数的,六年级女生人数所占扇形圆心角的度数为144°,也就是女生人数占全班人数的,五六年级女生占两个班总人数的,分别求出各选项中的两个班的女生人数是否占总人数的,据此解答.
13. 470007000 5
【分析】整数的写法:从高位到低位,一级一级地写,哪个数位上一个单位也没有,就在那个数位上写0;省略亿位后面的尾数求整数的近似数,也就是去掉亿位后面的尾数,对千万位上的数进行四舍五入,再在数的后面写上单位亿。
【详解】一个九位数,最高位上是4,千万位和千位都是7,其它各数位上都是0,这个数写作470007000;千万位上的数是7,7大于5,所以省略亿位后面的尾数约是5亿。
14.7
【分析】根据平行四边形的面积:底×高;三角形的面积:底×高÷2,由此可知等底等高的三角形面积等于平行四边形面积的一半,用三角形面积×2,即可解答。
【详解】3.5×2=7(平方米)
三角形的面积是3.5平方米,与它等底等高的平行四边形的面积是7平方米。
15.4
【分析】把12种属相看作12个抽屉,相当于要把47个人的属相放进12个抽屉里。根据抽屉原理:人数÷抽屉数=商……余数,按余数分类:①有余数,则至少有“商+1”人的属相是相同的;②没有余数,则至少有“商”人的属相是相同的。
【详解】47÷12=3(人)……11(人)
3+1=4(人)
即至少有4人的属相是相同的。
16.
【分析】用每天节约汽油升乘节约的天数,即可求出6天可节约汽油多少升。
【详解】×6=(升)
6天可节约汽油升。
17.4
【分析】根据图上距离=实际距离×比例尺,代入数据解答即可。注意单位要统一。
【详解】12米=1200厘米
1200×=4(厘米)
所以教学楼的宽在图上距离是4厘米。
18. 324 36
【分析】(1)根据题意,用一张长方形可以卷成两个形状不同的圆柱,一个圆柱是把长方形的长作为圆柱的底面周长,宽作为圆柱的高;另一个圆柱是把长方形的宽作为圆柱的底面周长,长作为圆柱的高;先根据圆的周长公式C=2πr可知,r=C÷π÷2,由此求出两种圆柱的底面半径;再根据圆柱的体积公式V=πr2h,求出两种圆柱的体积,再比较,得出最大圆柱体的体积。
(2)根据V柱=Sh,V锥=Sh可知,圆柱的高h柱=V÷S,圆锥的高h锥=3V÷S,所以当圆柱和圆锥等体积等底面积时,圆锥的高是圆柱高的3倍,用最大圆柱体的高乘3,即是与它体积相等底面积也相等的圆锥的高。
【详解】长方形的长:6π=6×3=18
长方形的宽:4π=4×3=12
(1)情况一:以长方形的长作为圆柱的底面周长,宽作为圆柱的高;
圆柱的底面半径:18÷3÷2=3
圆柱的体积:
3×32×12
=3×9×12
=324
情况二:以长方形的宽作为圆柱的底面周长,长作为圆柱的高;
圆柱的底面半径:12÷3÷2=2
圆柱的体积:
3×22×18
=3×4×18
=216
324>216
最大的圆柱体的体积是324。
(2)12×3=36
与它体积相等底面积也相等的圆锥的高是36。
19.24
【分析】二成就是20%,把去年收麦的重量看作单位“1”,今年收麦的重量=去年收麦的重量×(1+20%),据此解答。
【详解】二成=20%
20×(1+20%)
=20×1.2
=24(吨)
今年引用新品种后可收24吨小麦。
【点睛】本题考查成数问题以及求比一个数多百分之几的数是多少,用乘法计算。
20. 31 (3n+1)/(1+3n)
【分析】观察可知,1个正方形要用4根小棒,4=1×3+1,2个正方形要用7根小棒,7=2×3+1,3个正方形要用10根小棒,10=3×3+1…,由此可知,小棒根数=几个正方形就用几×3+1,据此分析。
【详解】10×3+1
=30+1
=31(根)
n×3+1=(3n+1)根
摆10个正方形要用31根小棒,摆个正方形要用(3n+1)根小棒。
21.见详解
【分析】由题意可知,图上1格表示200米,则
(1)人民广场到动物园的距离有600÷200=3格;
(2)少年宫到动物园的距离有300÷200=1.5格;
(3)动物园到图书馆的距离有400÷200=2格;动物园在图书馆南偏东30°方向,即图书馆在动物园的北偏西30°方向;再结合“上北下南,左西右东”及角度信息作图即可。
【详解】600÷200=3(格)
300÷200=1.5(格)
400÷200=2(格)
如图所示:
22.42本
【分析】把丽丽借阅的课外书籍的数量看作单位“1”,丽丽借书的本数的正好是强强的本数,即强强借的本数是丽丽的,用丽丽借阅课外书的本数×,即可求出强强借的本数,据此解答。
【详解】48×=42(本)
答:强强借了42本课外书籍。
【点睛】熟练掌握求一个数的几分之几是多少的计算方法是解答本题的关键。
23.0.65米
【分析】根据“学生身高大约比书桌高度的3倍少0.4米”可得出等量关系:书桌高度×3-0.4=学生身高,据此列出方程,并求解。
【详解】解:设所用书桌的高度应是米。
3-0.4=1.55
3=1.55+0.4
3=1.95
=1.95÷3
=0.65
答:所用书桌的高度应是0.65米。
24.亏了;50元
【分析】根据题意可知,一台售价是其原价的(1+20%),一台售价是其原价的(120%); 分别将两台饮水机的原价看作单位“1”,求单位“1”用除法计算,据此可得两款饮水机的原价; 最后将两台饮水机的原价相加,再与这两台饮水机的总售价进行比较,即可解答此题。
【详解】600÷(1+20%)
=600÷1.2
=500(元)
600÷(1-20%)
=600÷0.8
=750(元)
500+750=1250(元)
600+600=1200(元)
1250-1200=50(元)
答:这两台饮水机亏了,亏了50元。
【点睛】本题考查百分数,解答本题的关键是掌握题中的数量关系。
25.280本
【分析】由题意可知,图书馆新购进了840本新书,其中的借给了四年级,则剩下的本数占总本数的(1-),根据求一个数的几分之几是多少,用乘法计算,据此求出剩下的本数;然后把剩下的本数平均分成(5+4)份,进而求出1份表示的本数,六年级占4份,据此解答即可。
【详解】840×(1-)
=840×
=630(本)
630÷(5+4)×4
=630÷9×4
=70×4
=280(本)
答:六年级借到了280本新书。
26.9.6厘米
【分析】假设两个容器的高为x厘米,现将圆锥体容器装满水倒入圆柱体容器内,这时水深比圆柱体容器高度的低3厘米,则把圆柱的容器高度看作单位“1”,根据分数乘法的意义,圆柱现在的水深是(x-3)厘米,根据圆柱的体积公式:V=πr2h,和圆锥的体积公式:πr2h,列方程为×π×152×x=π×122×(x-3),然后解出方程即可。
【详解】解:设两个容器的高为x厘米。
×π×152×x=π×122×(x-3)
×π×225×x=π×144×(x-3)
×π×225×x÷π=π×144×(x-3)÷π
×225×x=144×(x-3)
75x=120x-432
120x-75x=432
45x=432
x=432÷45
x=9.6
答:这两个容器的高都是9.6厘米。
【点睛】本题主要考查了圆柱和圆锥的灵活应用,可用列方程解决问题,掌握相应的公式是解答本题的关键。
27.(1)甲分店:562.5万元;乙分店:592.5万元
(2)(答案不唯一,合理即可)见详解。
【分析】(1)分别把甲、乙两个分店四个季度的销售额加起来,再除以4即可;
(2)(答案不唯一,合理即可)观察复式折线统计图可知:甲分店从一季度到三季度呈下降趋势,三季度到四季度呈上升趋势;乙分店从一季度到二季度呈下降趋势,二季度到四季度呈上升趋势。根据两条折线的变化情况说明两个店的销售额情况即可。
(答案不唯一,合理即可)还能找到哪些数学信息,可比较某个季度两个店的销售额的高低。
【详解】(1)甲:(700+500+450+600)÷4
=2250÷4
=562.5(万元)
乙:(620+430+570+750)÷4
=2370÷4
=592.5(万元)
答:甲分店平均每个季度的销售额是562.5万元,乙分店平均每个季度的销售额是592.5万元。
(2)两个店销售额的变化情况:两个店的销售额都是先下降再上升。(答案不唯一)
还能从复式折线统计图上看出第四季度乙分店的销售额高于甲分店。(答案不唯一)
【点睛】此题考查的目的是能够根据统计图提供的信息,解决有关的实际问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
绝密★启用前
小升初分班考综合检测卷-数学六年级下册苏教版江苏地区适用
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、计算题
1.直接写得数。
10-9.94= 2.7×4×0.25= 30×30%=
2.用递等式计算,能简算的简算。
(1)3750÷(25+25×2) (2)×+80%÷
(3)5.75-(+) (4)+(0.75+0.25÷)
3.解方程或比例。
4.计算下图中阴影部分的面积。
二、选择题
5.妙想做抛硬币游戏(硬币是均匀的),前三次抛硬币的结果都是正面朝下,第四次正面朝上的可能性是( )。
A.0 B. C. D.1
6.算式1.2×3.2的积与两个因数比,( )。
A.比两个因数都大 B.比两个因数都小 C.与其中一个因数相等 D.无法确定
7.下图中有大小两个正方形,已知阴影部分的面积是5cm2,则圆环的面积是( )cm2。
A.6.28 B.15.7 C.18.84 D.28.26
8.甲乙的比为,甲数比乙数多______,乙数又比甲数少______,选项为( )。
A., B., C., D.,
9.下图表示两辆汽车所行驶的路程与相应时间关系的图象。下列关于图象描述错误的是( )。
A.两辆汽车行驶的路程和时间都是成正比例关系
B.从昆明到大理大约有350千米,①号车大约要4小时能到大理
C.从图象上看,①号车的速度比②号车快
D.从图象上看,②号车的速度比①号车快
10.一根长方体木料,长2米,宽和厚都是5米,把它锯成1米长的两段,表面积增加了( )平方米。
A.50 B.40 C.45 D.25
11.一个圆柱和一个圆锥的底面半径的比是3∶4,高度的比是2∶3,圆柱与圆锥的体积比( )。
A.1∶2 B.3∶2 C.9∶8 D.3∶8
12.小南统计学校五、六年级的男生和女生人数,制成了下面扇形统计图. 请你根据图中反映的男生女生人数的关系判断,下面说法可能正确的是( )
A.五年级160人,六年级200人 B.五年级200人,六年级225人
C.五年级200人,六年级160人 D.五年级250人,六年级200人
三、填空题
13.一个九位数,最高位是4,千万位和千位都是7,其他各个数位上都是0,这个数是( )。省略亿位后面的尾数约是( )亿。
14.三角形的面积是3.5平方米,与它等底等高的平行四边形的面积是( )平方米。
15.篮球兴趣小组有47人,至少有( )人的属相是相同的。
16.如果一辆汽车平均每天节约汽油升,6天可节约汽油( )升。
17.某学校教学楼的长为66米,宽12米,把它画在比例尺是1∶300的学校平面图上,教学楼的宽在图上距离是( )厘米。
18.将下图长方形卷成一个最大的圆柱体,体积是( );与它体积相等底面积也相等的圆锥的高是( )。(π取3)
19.今年市政府为了改善民生,提高粮食产量,引进了新的小麦品种中麦578,这个品种可比常规小麦增产二成,轩轩爷爷家去年收小麦20吨,今年引用新品种后可收( )吨小麦。
20.如图所示,摆10个正方形要用( )根小棒,摆个正方形要用( )根小棒。
正方形的个数 图形 小棒的根数
1 4
2 4+3
3 4+3+3
…… …… ……
四、作图题
21.位置与方向。在平面图上表示出各场所的位置。
(1)人民广场在动物园北偏东40°方向600米处。
(2)少年宫在动物园南偏西45°方向300米处。
(3)动物园在图书馆南偏东30°方向400米处。
五、解答题
22.在这学期的读书月活动中,丽丽共借阅了48本课外书籍。丽丽借书的本数的正好是强强的本数。强强借了多少本课外书籍?
23.高度适宜的书桌对孩子养成良好的体姿很重要。科学研究发现,学生身高大约比书桌高度的3倍少0.4米时最适合学生良好体姿的形成。照此推算,身高为1.55米的学生,所用书桌的高度应是多少米?(用方程解)
24.元旦节搞促销,两种品牌的饮水机各卖一台,售价都是600元,一台赚了20%,另一台亏20%,请你算一算这两台饮水机赚了还是亏了?赚(或亏)了多少元?
25.图书馆新购进了840本新书,其中的借给了四年级,剩下的书按5∶4借给五、六年级,六年级借到了多少本新书?
26.现有两个等高的容器(如图),圆锥体容器的半径是15厘米,圆柱体容器的半径是12厘米。现将圆锥体容器装满水倒入圆柱体容器内,这时水深比圆柱体容器高度的低3厘米。问:这两个容器的高是多少厘米?
27.下面是万家乐超市甲、乙两个分店去年四个季度的销售额统计图,请你看图回答问题。
(1)甲、乙两个分店平均每个季度的销售额各是多少万元?
(2)说说两个店销售额的变化情况,说说你还能找到哪些数学信息?(只要写一条就可以)
参考答案:
1.;0.06;2.7;9
2;;;
【详解】略
2.225;;4;
【分析】(1)可运用除法的性质将3750÷(25+25×2)转化为3750÷25+3750÷50,进行简便计算。
(2)将×+80%÷转化为×+×即可运用乘法分配律进行简算。
(3)5.75=5;所以原式=5--,由此进行简算。
(4)原式=+(+×),先计算括号里的乘法,再计算加法,最后计算括号外的加法。
【详解】(1)3750÷(25+25×2)
=3750÷25+3750÷50
=150+75
=225
(2)×+80%÷
=×+×
=×(+)
=×1
=
(3)5.75-(+)
=5--
=5-
=4
(4)+(0.75+0.25÷)
=+(+×)
=+(+)
=+()
=
=
【点睛】本题考查了数的简便计算;关键是要结合题意灵活运用运算律进行简算。
3.;;
【分析】,先将左边合并成,根据等式的性质2,两边同时÷即可;
,根据等式的性质1和2,两边同时+3×0.7的积,再同时÷4即可;
,根据比例的基本性质,先写成的形式,两边同时÷0.7即可。
【详解】
解:
解:
解:
4.86平方厘米
【分析】观察图形可知,阴影部分的面积=正方形的面积-圆的面积,根据正方形、圆的面积计算公式进行计算即可。
【详解】20×20-3.14×202×
=20×20-3.14×400×
=20×20-1256×
=400-314
=86(平方厘米)
所以,阴影部分的面积是86平方厘米。
5.B
【分析】硬币有正反两个面,每次抛硬币,正面和反面朝上的可能性都一样,根据分数的意义,确定正面朝上的可能性即可。
【详解】因为硬币有正反两个面,无论前三次抛硬币是什么结果,第四次正面朝上的可能性是。
故答案为:B
【点睛】只有在每个结果发生的可能性都相等的条件下才能表示出其发生的可能性。
6.A
【分析】一个数(0除外),乘大于1的数,积比原数大,据此分析。
【详解】1.2>1,3.2>1,1.2×3.2>1.2,1.2×3.2>3.2,算式1.2×3.2的积与两个因数比,比两个因数都大。
故答案为:A
【点睛】关键是掌握小数乘法的计算方法。
7.B
【分析】从图意可知,大正方形的边长=大圆半径,小正方形边长=小圆半径,阴影部分的面积=大正方形的面积-小正方形的面积=R2-r2=5cm2。圆环的面积:S=πR2-πr2=π(R2-r2)。所以用5×3.14即可求出圆环的面积。据此解答。
【详解】根据分析可得:
5×3.14=15.7(cm2)
圆环的面积是15.7 cm2。
故答案为:B
【点睛】理解大小正方形的面积差就是大小圆的半径平方差,是解题的关键。
8.B
【分析】根据“甲乙的比为”把甲看作5份,乙看作4份,先求出甲乙两数的差;
求甲数比乙数多百分之几,应该把乙数看作单位“1”,用两数差除以乙数;
求乙数比甲数少百分之几,应该把甲数看作单位“1”,用两数差除以甲数。
【详解】;
;
;
即甲数比乙数多,乙数比甲数少。
故答案为:B
9.D
【分析】正比例关系的图象是一条经过原点的直线;反比例关系的图象是一条不过原点的曲线;利用正比例和反比例的概念,以及统计图中的数据,逐项分析判断。
【详解】A.因为两辆汽车的图象都是一条经过原点的直线,所以两辆汽车行驶的路程和时间都是成正比例关系,原题说法正确;
B.从图象可以看出,从昆明到大理大约有350千米,①号车大约要4小时能到大理,原题说法正确;
C.从图象可以看出,①号车行360千米用时4小时,②号车行360千米用时8小时,路程相同时,时间越短,速度越快,所以①号车的速度比②号车快,原题说法正确;
D.由C可知,②号车的速度比①号车慢,原题说法错误。
故答案为:D
【点睛】掌握正比例关系的意义和图象的特征、以及折线统计图的特点和作用是解题的关键。
10.A
【分析】把它锯成1米长的两段,表面积增加了两个边长为5米的正方形面,利用正方形的面积公式,由此可以解决问题。
【详解】5×5×2
=25×2
=50(平方米)
表面积增加了50平方米。
故答案为:A
11.C
【分析】根据题意,设圆锥的底面半径为4r,则圆柱的半径为3r,设圆柱的高为2h,则圆锥的高为3h;根据圆柱的体积公式:底面积×高;圆锥的体积公式:底面积×高×,求出圆柱和圆锥的体积,再根据比的意义,用圆柱的体积∶圆锥的体积,化简即可解答。
【详解】解:设圆柱的底面半径是3r,则圆锥的底面半径是4r,设圆柱的高就是2h,则圆锥的高是3h,
那么圆柱的体积是:π×(3r)2×2h
=π×9r2×2h
=9πr2×2h
=18πr2h
圆锥的体积是:π×(4r)2×3h×
=π×16r2×3h×
=16πr2×3h×
=48πr2h×
=16πr2h
圆柱与圆锥的体积的比是:
18πr2h∶16πr2h
=18∶16
=(18÷2)∶(16÷2)
=9∶8
圆柱与圆锥的体积比是9∶8。
故答案为:C
【点睛】根据圆柱的体积公式、圆锥的体积公式以及比的意义进行解答。
12.A
【详解】五年级女生人数占全班人数:;六年级女生占全班人数;五六班女生人数占两个班总人数的
A、
B、
C、
D、
【点睛】根据扇形统计图可知:五年级女生人数所占扇形圆心角的度数为180°,也就是女生人数占全班人数的,六年级女生人数所占扇形圆心角的度数为144°,也就是女生人数占全班人数的,五六年级女生占两个班总人数的,分别求出各选项中的两个班的女生人数是否占总人数的,据此解答.
13. 470007000 5
【分析】整数的写法:从高位到低位,一级一级地写,哪个数位上一个单位也没有,就在那个数位上写0;省略亿位后面的尾数求整数的近似数,也就是去掉亿位后面的尾数,对千万位上的数进行四舍五入,再在数的后面写上单位亿。
【详解】一个九位数,最高位上是4,千万位和千位都是7,其它各数位上都是0,这个数写作470007000;千万位上的数是7,7大于5,所以省略亿位后面的尾数约是5亿。
14.7
【分析】根据平行四边形的面积:底×高;三角形的面积:底×高÷2,由此可知等底等高的三角形面积等于平行四边形面积的一半,用三角形面积×2,即可解答。
【详解】3.5×2=7(平方米)
三角形的面积是3.5平方米,与它等底等高的平行四边形的面积是7平方米。
15.4
【分析】把12种属相看作12个抽屉,相当于要把47个人的属相放进12个抽屉里。根据抽屉原理:人数÷抽屉数=商……余数,按余数分类:①有余数,则至少有“商+1”人的属相是相同的;②没有余数,则至少有“商”人的属相是相同的。
【详解】47÷12=3(人)……11(人)
3+1=4(人)
即至少有4人的属相是相同的。
16.
【分析】用每天节约汽油升乘节约的天数,即可求出6天可节约汽油多少升。
【详解】×6=(升)
6天可节约汽油升。
17.4
【分析】根据图上距离=实际距离×比例尺,代入数据解答即可。注意单位要统一。
【详解】12米=1200厘米
1200×=4(厘米)
所以教学楼的宽在图上距离是4厘米。
18. 324 36
【分析】(1)根据题意,用一张长方形可以卷成两个形状不同的圆柱,一个圆柱是把长方形的长作为圆柱的底面周长,宽作为圆柱的高;另一个圆柱是把长方形的宽作为圆柱的底面周长,长作为圆柱的高;先根据圆的周长公式C=2πr可知,r=C÷π÷2,由此求出两种圆柱的底面半径;再根据圆柱的体积公式V=πr2h,求出两种圆柱的体积,再比较,得出最大圆柱体的体积。
(2)根据V柱=Sh,V锥=Sh可知,圆柱的高h柱=V÷S,圆锥的高h锥=3V÷S,所以当圆柱和圆锥等体积等底面积时,圆锥的高是圆柱高的3倍,用最大圆柱体的高乘3,即是与它体积相等底面积也相等的圆锥的高。
【详解】长方形的长:6π=6×3=18
长方形的宽:4π=4×3=12
(1)情况一:以长方形的长作为圆柱的底面周长,宽作为圆柱的高;
圆柱的底面半径:18÷3÷2=3
圆柱的体积:
3×32×12
=3×9×12
=324
情况二:以长方形的宽作为圆柱的底面周长,长作为圆柱的高;
圆柱的底面半径:12÷3÷2=2
圆柱的体积:
3×22×18
=3×4×18
=216
324>216
最大的圆柱体的体积是324。
(2)12×3=36
与它体积相等底面积也相等的圆锥的高是36。
19.24
【分析】二成就是20%,把去年收麦的重量看作单位“1”,今年收麦的重量=去年收麦的重量×(1+20%),据此解答。
【详解】二成=20%
20×(1+20%)
=20×1.2
=24(吨)
今年引用新品种后可收24吨小麦。
【点睛】本题考查成数问题以及求比一个数多百分之几的数是多少,用乘法计算。
20. 31 (3n+1)/(1+3n)
【分析】观察可知,1个正方形要用4根小棒,4=1×3+1,2个正方形要用7根小棒,7=2×3+1,3个正方形要用10根小棒,10=3×3+1…,由此可知,小棒根数=几个正方形就用几×3+1,据此分析。
【详解】10×3+1
=30+1
=31(根)
n×3+1=(3n+1)根
摆10个正方形要用31根小棒,摆个正方形要用(3n+1)根小棒。
21.见详解
【分析】由题意可知,图上1格表示200米,则
(1)人民广场到动物园的距离有600÷200=3格;
(2)少年宫到动物园的距离有300÷200=1.5格;
(3)动物园到图书馆的距离有400÷200=2格;动物园在图书馆南偏东30°方向,即图书馆在动物园的北偏西30°方向;再结合“上北下南,左西右东”及角度信息作图即可。
【详解】600÷200=3(格)
300÷200=1.5(格)
400÷200=2(格)
如图所示:
22.42本
【分析】把丽丽借阅的课外书籍的数量看作单位“1”,丽丽借书的本数的正好是强强的本数,即强强借的本数是丽丽的,用丽丽借阅课外书的本数×,即可求出强强借的本数,据此解答。
【详解】48×=42(本)
答:强强借了42本课外书籍。
【点睛】熟练掌握求一个数的几分之几是多少的计算方法是解答本题的关键。
23.0.65米
【分析】根据“学生身高大约比书桌高度的3倍少0.4米”可得出等量关系:书桌高度×3-0.4=学生身高,据此列出方程,并求解。
【详解】解:设所用书桌的高度应是米。
3-0.4=1.55
3=1.55+0.4
3=1.95
=1.95÷3
=0.65
答:所用书桌的高度应是0.65米。
24.亏了;50元
【分析】根据题意可知,一台售价是其原价的(1+20%),一台售价是其原价的(120%); 分别将两台饮水机的原价看作单位“1”,求单位“1”用除法计算,据此可得两款饮水机的原价; 最后将两台饮水机的原价相加,再与这两台饮水机的总售价进行比较,即可解答此题。
【详解】600÷(1+20%)
=600÷1.2
=500(元)
600÷(1-20%)
=600÷0.8
=750(元)
500+750=1250(元)
600+600=1200(元)
1250-1200=50(元)
答:这两台饮水机亏了,亏了50元。
【点睛】本题考查百分数,解答本题的关键是掌握题中的数量关系。
25.280本
【分析】由题意可知,图书馆新购进了840本新书,其中的借给了四年级,则剩下的本数占总本数的(1-),根据求一个数的几分之几是多少,用乘法计算,据此求出剩下的本数;然后把剩下的本数平均分成(5+4)份,进而求出1份表示的本数,六年级占4份,据此解答即可。
【详解】840×(1-)
=840×
=630(本)
630÷(5+4)×4
=630÷9×4
=70×4
=280(本)
答:六年级借到了280本新书。
26.9.6厘米
【分析】假设两个容器的高为x厘米,现将圆锥体容器装满水倒入圆柱体容器内,这时水深比圆柱体容器高度的低3厘米,则把圆柱的容器高度看作单位“1”,根据分数乘法的意义,圆柱现在的水深是(x-3)厘米,根据圆柱的体积公式:V=πr2h,和圆锥的体积公式:πr2h,列方程为×π×152×x=π×122×(x-3),然后解出方程即可。
【详解】解:设两个容器的高为x厘米。
×π×152×x=π×122×(x-3)
×π×225×x=π×144×(x-3)
×π×225×x÷π=π×144×(x-3)÷π
×225×x=144×(x-3)
75x=120x-432
120x-75x=432
45x=432
x=432÷45
x=9.6
答:这两个容器的高都是9.6厘米。
【点睛】本题主要考查了圆柱和圆锥的灵活应用,可用列方程解决问题,掌握相应的公式是解答本题的关键。
27.(1)甲分店:562.5万元;乙分店:592.5万元
(2)(答案不唯一,合理即可)见详解。
【分析】(1)分别把甲、乙两个分店四个季度的销售额加起来,再除以4即可;
(2)(答案不唯一,合理即可)观察复式折线统计图可知:甲分店从一季度到三季度呈下降趋势,三季度到四季度呈上升趋势;乙分店从一季度到二季度呈下降趋势,二季度到四季度呈上升趋势。根据两条折线的变化情况说明两个店的销售额情况即可。
(答案不唯一,合理即可)还能找到哪些数学信息,可比较某个季度两个店的销售额的高低。
【详解】(1)甲:(700+500+450+600)÷4
=2250÷4
=562.5(万元)
乙:(620+430+570+750)÷4
=2370÷4
=592.5(万元)
答:甲分店平均每个季度的销售额是562.5万元,乙分店平均每个季度的销售额是592.5万元。
(2)两个店销售额的变化情况:两个店的销售额都是先下降再上升。(答案不唯一)
还能从复式折线统计图上看出第四季度乙分店的销售额高于甲分店。(答案不唯一)
【点睛】此题考查的目的是能够根据统计图提供的信息,解决有关的实际问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
