小升初分班考模拟测试卷(含答案)数学六年级下册苏教版江苏地区适用
文档属性
| 名称 | 小升初分班考模拟测试卷(含答案)数学六年级下册苏教版江苏地区适用 |  | |
| 格式 | docx | ||
| 文件大小 | 574.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-05 09:28:17 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
绝密★启用前
小升初分班考模拟测试卷-数学六年级下册苏教版江苏地区适用
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、计算题
1.直接写出得数。
36×= ×= ÷= 2.8×=
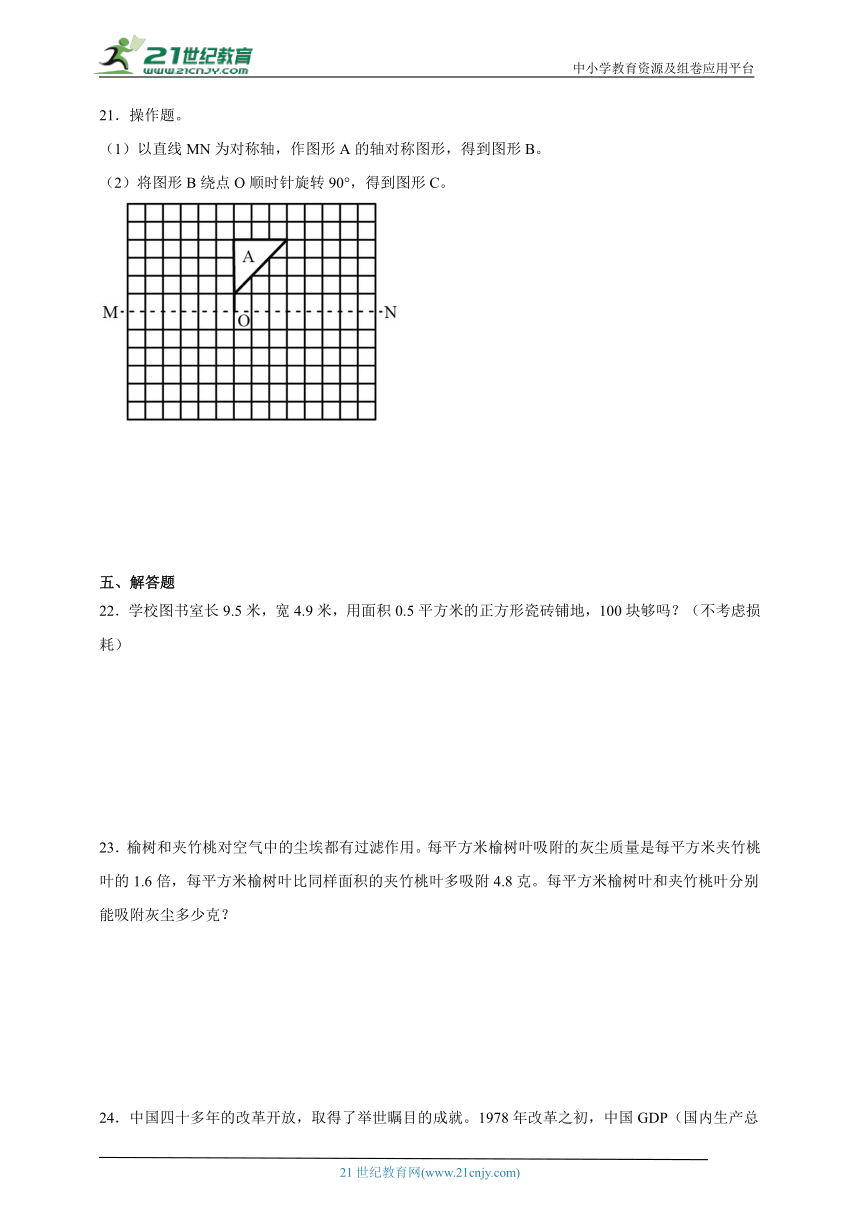
×= 25÷= ÷5%= +÷+=
2.下面各题,怎样算简便就怎样算。
-+- 0.25×3.2×1.25
64÷+37×40%-0.4
3.解方程或比例。
1-25%x=0.5 0.3x-4.4=1 ∶x=∶
4.求下图阴影部分的周长。
二、选择题
5.把约分成,下面对“变化”与“不变”的描述正确的是( )。
A.分数大小不变,分数单位变小 B.分数大小不变,分数单位变大
C.分数变大,分数单位不变 D.分数变小,分数单位不变
6.边长分米的正方形的周长是( )分米。
A.2 B.6 C.10 D.12
7.把20本练习本叠成一个长方体(如图),量出前面长方形的长和宽,算出它的面积。再把这叠练习本均匀地斜放,这时前面变成了一个近似的平行四边形。它的面积与原来长方形面积相比,( )。
A.不变 B.变大了 C.变小了 D.以上都有可能
8.水结成冰后体积是原来的1.1倍,冰的体积比水增加了( )。
A.10% B.110% C. D.
9.有一盒棋子,黑子与白子的比是4∶5,下面说法错误的是( )。
A.黑子是白子的 B.白子是黑子的
C.黑子是棋子总数的 D.白子比黑子多
10.一根52cm长的铁丝,正好可以焊成一个长为6cm、宽为4cm、高为( )的长方体框架。
A.2cm B.3cm C.4cm D.5cm
11.一个圆柱和一个圆锥等底等高,它们的体积之和是52dm ,那么这个圆柱的体积是( )dm 。
A.13 B.26 C.39 D.无法确定
12.如图,按这样的规律第7个图形有( )个点。
A.21 B.25 C.28 D.29
三、填空题
13.一个十位数,最高位是6,百万位和百位都是5,其他各数位上都是0,这个数写作( ),最高位上的“6”表示6个( ),“四舍五入”到亿位约是( )亿。
14.果园里苹果树的棵数是梨树的2.5倍,当梨树有x棵时,果园里一共有果树( )棵;当x为200时,果园里一共有( )棵果树。
15.有80盒饼干,其中79盒质量相同,另有1盒少了几块。假如用天平称,至少称( )次能保证找出这盒饼干。
16.阳光小学举行绘画活动,四年级共制作12幅作品,五年级的作品数量是四年级的,六年级的作品数量是五年级的。六年级共制作( )幅作品。
17.甲数和乙数的比是4∶7,则甲数占乙数的;甲数比乙数少,乙数比甲数多。
18.一个正方体的体积是240立方厘米,把它削成一个最大的圆锥,那么圆锥的体积是( )立方厘米。
19.科学家做育种实验,发现此批次种子出芽率为95%,有3颗种子没发芽,此次实验种子一共( )颗。
20.照此规律画下去,第n个图形共有( )个,( )个。
四、作图题
21.操作题。
(1)以直线MN为对称轴,作图形A的轴对称图形,得到图形B。
(2)将图形B绕点O顺时针旋转90°,得到图形C。
五、解答题
22.学校图书室长9.5米,宽4.9米,用面积0.5平方米的正方形瓷砖铺地,100块够吗?(不考虑损耗)
23.榆树和夹竹桃对空气中的尘埃都有过滤作用。每平方米榆树叶吸附的灰尘质量是每平方米夹竹桃叶的1.6倍,每平方米榆树叶比同样面积的夹竹桃叶多吸附4.8克。每平方米榆树叶和夹竹桃叶分别能吸附灰尘多少克?
24.中国四十多年的改革开放,取得了举世瞩目的成就。1978年改革之初,中国GDP(国内生产总值)仅0.15万亿美元,不足当时世界第一的美国GDP2.35万亿美元的零头。2019年中国GDP已超过了14万亿美元,大约相当于美国2019年GDP的70%。国际权威机构预测,按当下的发展势头,再用不到十年时间,中国将超越美国,成为世界第一。请问2019年美国的GDP大约是多少万亿美元?
25.苍中七年级学生分三组参加植树,第一组与第二组的人数比是5∶4,第二组与第三组的人数比是3∶2,第一组人数比第二组与第三组人数的总和少20人,七年级参加植树的共有多少人?
26.如图,一个圆锥型生日帽的底面周长是56.52厘米,它的高与底面直径相等。这个生日帽的体积是多少立方厘米?
27.学校进行学生体质达标测试,六年级100米短跑测试情况如下图所示。其中达到优秀的有90人。
(1)六年级参加本次测试的学生一共有多少人?
(2)六年级不及格的学生有多少人?
(3)针对这次测试结果,如果你是该校校长,你有什么想法?
参考答案:
1.6;;;2.1
;45;4;5
【详解】略
2.;1
;40
【分析】-+-,交换中间减数和加数的位置,根据减法的性质,将后两个数先加起来再计算;
0.25×3.2×1.25,将3.2拆成(4×0.8),利用乘法交换结合律进行简算;
,先算加法,再算乘法,最后算除法;
64÷+37×40%-0.4,将除法改写成乘法,并将分数和百分数都化成小数,利用乘法分配律进行简算。
【详解】-+-
=(+)-(+)
=1-
=
0.25×3.2×1.25
=0.25×(4×0.8)×1.25
=(0.25×4)×(0.8×1.25)
=1×1
=1
64÷+37×40%-0.4
=64×+37×0.4-0.4
=64×0.4+37×0.4-0.4
=(64+37-1)×0.4
=100×0.4
=40
3.x=2;x=18;x=
【分析】(1)先左右两边同时加上0.25x,化成0.5+0.25x=1,再两边同时减去0.5,最后两边同时除以0.25;
(2)先左右两边同时加上4.4,再两边同时除以0.3;
(3)根据两内项积等于两外项积,先把原式化成x=×,再两边同时除以即可。
【详解】1-25%x=0.5
解:1-0.25x+0.25x=0.5+0.25x
0.5+0.25x=1
0.5+0.25x-0.5=1-0.5
0.25x÷0.25=0.5÷0.25
x=2
0.3x-4.4=1
解:0.3x-4.4+4.4=1+4.4
0.3x=5.4
0.3x÷0.3=5.4÷0.3
x=18
∶x=∶
解:x=×
x÷=÷
x=×
x=
4.31.4厘米
【分析】观察图形可知:阴影部分的周长包括以5厘米为半径的圆周长的一半和两个以5厘米为直径的半圆弧,而两个以5厘米为直径的半圆弧可以组成一个小圆。圆的周长=πd=2πr,据此求出圆周长的一半和组成的小圆的周长,再把它们相加即可解答。
【详解】5×2×3.14÷2+3.14×5
=31.4÷2+15.7
=15.7+15.7
=31.4(厘米)
则阴影部分的周长是31.4厘米。
5.B
【分析】分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。由此可知分数大小不变;分数单位:把单位“1”平均分成若干份,这样的一份或几份都可以用分数来表示,表示其中一份的数叫作分数单位。据此找出两个分数的分数单位,将分数单位进行比较即可。
【详解】由分数的基本性质可知,把约分成,分数大小不变;
的分数单位是,的分数单位是,<;
所以把约分成,分数大小不变,分数单位变大。
故答案为:B
6.A
【分析】根据正方形周长公式:周长=边长×4,代入数据,即可解答。
【详解】×4=2(分米)
边长分米的正方形的周长是2分米。
故答案为:A
7.A
【分析】摆成长方体时前面的长方形是由这些练习本的侧面组成的,当他们均匀斜放时变成的平行四边形依旧是由这几本练习本的侧面组成的.所以面积大小不变。
【详解】长方体的长是2厘米,宽是1厘米,前面长方形的面积是:2×1=2(平方厘米)
当这叠练习本均匀地斜放,这时前面变成了一个近似的平行长四边形,平行四边行的底是2厘米,高是1厘米,平行四边形面积:2×1=2(平方厘米)。
故答案为:A
【点睛】掌握长方形和平行四边形面积计算公式是解答的关键。
8.A
【分析】水结成冰后体积是原来的1.1倍,将水的体积看作1,则冰的体积是1.1,冰和水的体积差÷水的体积=冰的体积比水增加了几分之几或百分之几,据此列式计算。
【详解】(1.1-1)÷1
=0.1÷1
=0.1
=10%
=
冰的体积比水增加了10%或。
故答案为:A
9.D
【分析】黑子与白子的比是4∶5,把黑子的颗数看成4份,那么白子的颗数就是5份,总份数就是4+5=9(份)。求A是B的几分之几问题,用A除以B;求A比B多几分之几,用A与B的差除以B,据此解答。
【详解】A.黑子是白子的几分之几,4÷5=,该选项正确;
B.白子是黑子的几分之几,5÷4=,该选项正确;
C.黑子是棋子总数的几分之几,4÷(4+5)=,该选项正确;
D.白子比黑子多几分之几,(5-4)÷4=≠,该选项错误。
故答案为:D
【点睛】本题考查比的意义及用分数除法解决问题。求A是B的几分之几问题,用A除以B解答;求A比B多几分之几的问题,用A与B的差除以B解答。
10.B
【分析】根据题意,用一根铁丝焊成一个长方体框架,那么这根铁丝的长度等于长方体的棱长总和;
根据长方体的棱长总和=(长+宽+高)×4,可知长方体的长、宽、高之和=棱长总和÷4,然后用长、宽、高之和减去长、宽,即可求出这个长方体的高。
【详解】52÷4=13(cm)
13-6-4=3(cm)
长方体的高为3cm。
故答案为:B
11.C
【解析】圆柱与圆锥等底等高,那么圆柱体积是圆锥体积的3倍,它们的体积之和是52dm ,根据和倍问题规律解答。
【详解】52÷(1+3)
=52÷4
=13(dm )
13×3=39(dm )
故答案为:C
【点睛】和倍问题:和÷(倍数+1)=小数;小数×倍数=大数或者和-小数=大数。
12.B
【分析】由题意可知,第一个图形有1个点,第二个图形有5个点,第三个图形有9个点,以此类推第n个图形则有1+(n-1)×4个点。
【详解】由分析可知,第7个图形有:
1+(7-1)×4
=1+6×4
=1+24
=25(个)
所以,第7个图形有25个点。
故答案为:B
【点睛】要考查了学生通过特例分析从而归纳总结出一般结论的能力。对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解。
13. 6005000500 十亿 60
【分析】整数的写法:先写亿级,再写万级,最后写个级。哪个数位上一个单位也没有,就在那个数位上写0。“6”在十亿位,表示6个十亿。省略亿后面的尾数,要看千万位上的数,根据四舍五入法的原则,若千万位上的数字大于等于5,就向亿位进1;若千万位上的数字小于5,就舍去千万位及其后面数位上的数。
【详解】一个十位数,最高位是6,百万位和百位都是5,其他各数位上都是0,这个数写作6005000500,最高位上的“6”表示6个十亿,“四舍五入”到亿位约是60亿。
14. 3.5x 700
【分析】求一个数的几倍是多少,用乘法计算;当梨树有x棵时,那么苹果树有2.5x棵,将梨树和苹果树相加,可以得到果园里一共有果树多少棵;将x=200代入算式,计算出结果即可;据此解答。
【详解】根据分析:x+2.5x=(1+2.5)x=3.5x(棵),所以果园里一共有果树3.5x棵;3.5x=3.5×200=700(棵),所以当x为200时,果园里一共有700棵果树。
15.4
【分析】把80盒饼干分成3份,即(27,27,26),第一次称,天平两边各放27盒,如果天平不平衡,次品就在较轻的27盒中;如果天平平衡,次品在剩下的26盒中;
考虑最不利原则,次品在数量多的里面,把有次品的27盒饼干平均分成3份,即(9,9,9),第二次称,天平两边各放9盒,如果天平不平衡,次品就在较轻的9盒中;如果天平平衡,次品在剩下的9盒中;
再把有次品的9盒饼干平均分成3份,即(3,3,3),第三次称,天平两边各放3盒,如果天平不平衡,次品就在较轻的3盒中;如果天平平衡,次品就在剩下的3盒中;
最后把有次品的3盒饼干平均分成3份,即(1,1,1),第四次称,天平两边各放1盒,天平不平衡,次品就是较轻的那盒;如果天平平衡,次品就是剩下的那盒。
所以至少称4次能保证找出这盒饼干。
【详解】
假如用天平称,至少称4次能保证找出这盒饼干。
16.14
【分析】把四年级的作品数量看作单位“1”,五年级的作品数量是四年级的,求五年级作品数量,用四年级的作品数量×,求出五年级的作品数量;再把五年级的作品数量看作单位“1”,六年级的作品数量是五年级的,求六年级的作品数量,用五年级的作品数量×,即可求出六年级的作品数量,据此解答。
【详解】12××
=10×
=14(幅)
阳光小学举行绘画活动,四年级共制作12幅作品,五年级的作品数量是四年级的,六年级的作品数量是五年级的。六年级共制作14幅作品。
17.;;
【分析】甲数和乙数的比是4∶7,将甲数看作4,乙数看作7,甲数÷乙数=甲数占乙数的几分之几;甲乙两数差÷乙数=甲数比乙数少几分之几;甲乙两数差÷甲数=乙数比甲数多几分之几。
【详解】4÷7=
(7-4)÷7
=3÷7
=
(7-4)÷4
=3÷4
=
甲数和乙数的比是4∶7,则甲数占乙数的;甲数比乙数少,乙数比甲数多。
【点睛】关键是理解比的意义,求一个数占另一个数的几分之几用除法,差÷较大数=少几分之几,差÷较小数=多几分之几。
18.62.8
【分析】削成的最大的圆锥的底面直径等于正方体的棱长,高也等于正方体的棱长,那么,然后根据圆锥的体积公式解答即可。
【详解】用字母表示正方形的棱长,则。
(立方厘米)
当取近似值3.14时,(立方厘米)。
【点睛】本题考查了圆锥的体积公式的灵活应用,本题的关键是得到最大的圆锥的直径和高与正方体的关系。
19.60
【分析】把这批种子的总数量看作单位“1”,已知此批次种子出芽率为95%,则没出芽的数量占总数量的(1-95%),根据百分数除法的意义,用3÷(1-95%)即可求出总数量。
【详解】3÷(1-95%)
=3÷5%
=60(颗)
此次实验种子一共60颗。
20. n 2n+6
【分析】(1)第1个图形有1个,第2个图形有2个,第3个图形有3个,第4个图形有4个,……由此发现规律:第几个图形就有几个。
(2)每个图形最左侧有3个,最右侧有3个,3+3=6(个);第1个图形有2+6=8个,第2个图形有2×2+6=10个,第3个图形有2×3+6=12个,第4个图形有2×4+6=14个,……由此发现规律:第几个图形就有几个2加6个。
【详解】由发现的规律可知:第n个图形共有n个,(2n+6)个。
【点睛】在运用数形结合的方法探究数学规律时,一定要把图形和数一一对应。
21.见详解
【分析】(1)补全轴对称图形的方法:找出图形A的关键点,依据对称轴直线MN画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形B。
(2)根据旋转的特征,将图形B绕点O顺时针旋转90°,点B位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形C。
【详解】如图:
【点睛】此题主要考查补全轴对称图形以及图形的旋转,掌握其作图方法是解题的关键。
22.够
【分析】根据长方形面积=长×宽,求出图书室面积,图书室面积÷瓷砖面积=需要的瓷砖块数,结果用进一法保留近似数,比较即可。
【详解】
(块)
答:100块够。
【点睛】关键是掌握小数乘除法的计算方法,理解用进一法保留近似数的实际意义。
23.12.8克;8克
【分析】求一个数的几倍是多少用乘法,设每平方米夹竹桃叶能吸附灰尘x克,则每平方米榆树叶能吸附灰尘1.6x克,根据每平方米榆树叶能吸附灰尘质量-每平方米夹竹桃叶能吸附灰尘质量=4.8克,列出方程求出x的值,是每平方米夹竹桃叶能吸附灰尘质量,每平方米夹竹桃叶能吸附灰尘质量×1.6=每平方米榆树叶能吸附灰尘质量。
【详解】解:设每平方米夹竹桃叶能吸附灰尘x克。
1.6x-x=4.8
0.6x=4.8
0.6x÷0.6=4.8÷0.6
x=8
8×1.6=12.8(克)
答:每平方米榆树叶和夹竹桃叶分别能吸附灰尘12.8克、8克。
24.20万亿美元
【分析】把美国2019年GDP看作单位“1”,根据百分数除法的意义,用14÷70%即可求出2019年美国的GDP。
【详解】14÷70%=20(万亿美元)
答:2019年美国的GDP大约是20万亿美元。
25.140人
【分析】七年级学生分三组参加,第一组与第二组人数的比是5∶4,第二组和第三组人数的比是3∶2,可知一、二、三组的人数比是15∶12∶8,根据比与分数的关系可知:第一小组占总人数的,第二、三小组占总人数的,第一小组比第二与三组人数总和少20人,用第二、三组占的总数的几分之几减去第一组占总人数的几分之几,就是20对应的分率,据此解答。
【详解】20÷(-)
=20÷(-)
=20÷
=140(人)
答:七年级参加植树的共有140人。
【点睛】本题的关键是先求出三个班人数的比,然后求出20对应的分率,再根据分数除法的意义列式解答。
26.1526.04立方厘米
【分析】圆锥型的底面周长即圆的周长,根据圆的周长=求出圆的半径,圆的高与圆的直径相同,即h=2r,根据圆锥的体积=,求出生日帽的体积。
【详解】56.52÷(3.14×2)
=56.52÷6.28
=9(厘米)
9×2=18(厘米)
答:这个生日帽的体积是1526.04立方厘米。
27.(1)600人
(2)30人
(3)增加学生体育锻炼的时间,适当增加锻炼的强度
【分析】(1)把六年级的总人数看作单位“1”,用达到优秀的人数除以对应分率等于六年级参加本次测试的总人数。
(2)把六年级的总人数看作单位“1”,用单位“1”减去优秀、及格、良好人数所占的分率,求出不及格人数所占的分率,再用六年级参加本次测试的总人数乘不及格人数对应的分率即可解答。
(3)根据这次测试结果给出合理建议即可。
【详解】(1)90÷15%=600(人)
答:六年级参加本次测试的学生一共有600人。
(2)1-30%-50%-15%
=70%-50%-15%
=20%-15%
=5%
600×5%=30(人)
答:六年级不及格的学生有30人。
(3)如果我是该校校长,增加学生体育锻炼的时间,适当增加锻炼的强度。(答案不唯一)
【点睛】利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数相关解题思路解答即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
绝密★启用前
小升初分班考模拟测试卷-数学六年级下册苏教版江苏地区适用
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、计算题
1.直接写出得数。
36×= ×= ÷= 2.8×=
×= 25÷= ÷5%= +÷+=
2.下面各题,怎样算简便就怎样算。
-+- 0.25×3.2×1.25
64÷+37×40%-0.4
3.解方程或比例。
1-25%x=0.5 0.3x-4.4=1 ∶x=∶
4.求下图阴影部分的周长。
二、选择题
5.把约分成,下面对“变化”与“不变”的描述正确的是( )。
A.分数大小不变,分数单位变小 B.分数大小不变,分数单位变大
C.分数变大,分数单位不变 D.分数变小,分数单位不变
6.边长分米的正方形的周长是( )分米。
A.2 B.6 C.10 D.12
7.把20本练习本叠成一个长方体(如图),量出前面长方形的长和宽,算出它的面积。再把这叠练习本均匀地斜放,这时前面变成了一个近似的平行四边形。它的面积与原来长方形面积相比,( )。
A.不变 B.变大了 C.变小了 D.以上都有可能
8.水结成冰后体积是原来的1.1倍,冰的体积比水增加了( )。
A.10% B.110% C. D.
9.有一盒棋子,黑子与白子的比是4∶5,下面说法错误的是( )。
A.黑子是白子的 B.白子是黑子的
C.黑子是棋子总数的 D.白子比黑子多
10.一根52cm长的铁丝,正好可以焊成一个长为6cm、宽为4cm、高为( )的长方体框架。
A.2cm B.3cm C.4cm D.5cm
11.一个圆柱和一个圆锥等底等高,它们的体积之和是52dm ,那么这个圆柱的体积是( )dm 。
A.13 B.26 C.39 D.无法确定
12.如图,按这样的规律第7个图形有( )个点。
A.21 B.25 C.28 D.29
三、填空题
13.一个十位数,最高位是6,百万位和百位都是5,其他各数位上都是0,这个数写作( ),最高位上的“6”表示6个( ),“四舍五入”到亿位约是( )亿。
14.果园里苹果树的棵数是梨树的2.5倍,当梨树有x棵时,果园里一共有果树( )棵;当x为200时,果园里一共有( )棵果树。
15.有80盒饼干,其中79盒质量相同,另有1盒少了几块。假如用天平称,至少称( )次能保证找出这盒饼干。
16.阳光小学举行绘画活动,四年级共制作12幅作品,五年级的作品数量是四年级的,六年级的作品数量是五年级的。六年级共制作( )幅作品。
17.甲数和乙数的比是4∶7,则甲数占乙数的;甲数比乙数少,乙数比甲数多。
18.一个正方体的体积是240立方厘米,把它削成一个最大的圆锥,那么圆锥的体积是( )立方厘米。
19.科学家做育种实验,发现此批次种子出芽率为95%,有3颗种子没发芽,此次实验种子一共( )颗。
20.照此规律画下去,第n个图形共有( )个,( )个。
四、作图题
21.操作题。
(1)以直线MN为对称轴,作图形A的轴对称图形,得到图形B。
(2)将图形B绕点O顺时针旋转90°,得到图形C。
五、解答题
22.学校图书室长9.5米,宽4.9米,用面积0.5平方米的正方形瓷砖铺地,100块够吗?(不考虑损耗)
23.榆树和夹竹桃对空气中的尘埃都有过滤作用。每平方米榆树叶吸附的灰尘质量是每平方米夹竹桃叶的1.6倍,每平方米榆树叶比同样面积的夹竹桃叶多吸附4.8克。每平方米榆树叶和夹竹桃叶分别能吸附灰尘多少克?
24.中国四十多年的改革开放,取得了举世瞩目的成就。1978年改革之初,中国GDP(国内生产总值)仅0.15万亿美元,不足当时世界第一的美国GDP2.35万亿美元的零头。2019年中国GDP已超过了14万亿美元,大约相当于美国2019年GDP的70%。国际权威机构预测,按当下的发展势头,再用不到十年时间,中国将超越美国,成为世界第一。请问2019年美国的GDP大约是多少万亿美元?
25.苍中七年级学生分三组参加植树,第一组与第二组的人数比是5∶4,第二组与第三组的人数比是3∶2,第一组人数比第二组与第三组人数的总和少20人,七年级参加植树的共有多少人?
26.如图,一个圆锥型生日帽的底面周长是56.52厘米,它的高与底面直径相等。这个生日帽的体积是多少立方厘米?
27.学校进行学生体质达标测试,六年级100米短跑测试情况如下图所示。其中达到优秀的有90人。
(1)六年级参加本次测试的学生一共有多少人?
(2)六年级不及格的学生有多少人?
(3)针对这次测试结果,如果你是该校校长,你有什么想法?
参考答案:
1.6;;;2.1
;45;4;5
【详解】略
2.;1
;40
【分析】-+-,交换中间减数和加数的位置,根据减法的性质,将后两个数先加起来再计算;
0.25×3.2×1.25,将3.2拆成(4×0.8),利用乘法交换结合律进行简算;
,先算加法,再算乘法,最后算除法;
64÷+37×40%-0.4,将除法改写成乘法,并将分数和百分数都化成小数,利用乘法分配律进行简算。
【详解】-+-
=(+)-(+)
=1-
=
0.25×3.2×1.25
=0.25×(4×0.8)×1.25
=(0.25×4)×(0.8×1.25)
=1×1
=1
64÷+37×40%-0.4
=64×+37×0.4-0.4
=64×0.4+37×0.4-0.4
=(64+37-1)×0.4
=100×0.4
=40
3.x=2;x=18;x=
【分析】(1)先左右两边同时加上0.25x,化成0.5+0.25x=1,再两边同时减去0.5,最后两边同时除以0.25;
(2)先左右两边同时加上4.4,再两边同时除以0.3;
(3)根据两内项积等于两外项积,先把原式化成x=×,再两边同时除以即可。
【详解】1-25%x=0.5
解:1-0.25x+0.25x=0.5+0.25x
0.5+0.25x=1
0.5+0.25x-0.5=1-0.5
0.25x÷0.25=0.5÷0.25
x=2
0.3x-4.4=1
解:0.3x-4.4+4.4=1+4.4
0.3x=5.4
0.3x÷0.3=5.4÷0.3
x=18
∶x=∶
解:x=×
x÷=÷
x=×
x=
4.31.4厘米
【分析】观察图形可知:阴影部分的周长包括以5厘米为半径的圆周长的一半和两个以5厘米为直径的半圆弧,而两个以5厘米为直径的半圆弧可以组成一个小圆。圆的周长=πd=2πr,据此求出圆周长的一半和组成的小圆的周长,再把它们相加即可解答。
【详解】5×2×3.14÷2+3.14×5
=31.4÷2+15.7
=15.7+15.7
=31.4(厘米)
则阴影部分的周长是31.4厘米。
5.B
【分析】分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。由此可知分数大小不变;分数单位:把单位“1”平均分成若干份,这样的一份或几份都可以用分数来表示,表示其中一份的数叫作分数单位。据此找出两个分数的分数单位,将分数单位进行比较即可。
【详解】由分数的基本性质可知,把约分成,分数大小不变;
的分数单位是,的分数单位是,<;
所以把约分成,分数大小不变,分数单位变大。
故答案为:B
6.A
【分析】根据正方形周长公式:周长=边长×4,代入数据,即可解答。
【详解】×4=2(分米)
边长分米的正方形的周长是2分米。
故答案为:A
7.A
【分析】摆成长方体时前面的长方形是由这些练习本的侧面组成的,当他们均匀斜放时变成的平行四边形依旧是由这几本练习本的侧面组成的.所以面积大小不变。
【详解】长方体的长是2厘米,宽是1厘米,前面长方形的面积是:2×1=2(平方厘米)
当这叠练习本均匀地斜放,这时前面变成了一个近似的平行长四边形,平行四边行的底是2厘米,高是1厘米,平行四边形面积:2×1=2(平方厘米)。
故答案为:A
【点睛】掌握长方形和平行四边形面积计算公式是解答的关键。
8.A
【分析】水结成冰后体积是原来的1.1倍,将水的体积看作1,则冰的体积是1.1,冰和水的体积差÷水的体积=冰的体积比水增加了几分之几或百分之几,据此列式计算。
【详解】(1.1-1)÷1
=0.1÷1
=0.1
=10%
=
冰的体积比水增加了10%或。
故答案为:A
9.D
【分析】黑子与白子的比是4∶5,把黑子的颗数看成4份,那么白子的颗数就是5份,总份数就是4+5=9(份)。求A是B的几分之几问题,用A除以B;求A比B多几分之几,用A与B的差除以B,据此解答。
【详解】A.黑子是白子的几分之几,4÷5=,该选项正确;
B.白子是黑子的几分之几,5÷4=,该选项正确;
C.黑子是棋子总数的几分之几,4÷(4+5)=,该选项正确;
D.白子比黑子多几分之几,(5-4)÷4=≠,该选项错误。
故答案为:D
【点睛】本题考查比的意义及用分数除法解决问题。求A是B的几分之几问题,用A除以B解答;求A比B多几分之几的问题,用A与B的差除以B解答。
10.B
【分析】根据题意,用一根铁丝焊成一个长方体框架,那么这根铁丝的长度等于长方体的棱长总和;
根据长方体的棱长总和=(长+宽+高)×4,可知长方体的长、宽、高之和=棱长总和÷4,然后用长、宽、高之和减去长、宽,即可求出这个长方体的高。
【详解】52÷4=13(cm)
13-6-4=3(cm)
长方体的高为3cm。
故答案为:B
11.C
【解析】圆柱与圆锥等底等高,那么圆柱体积是圆锥体积的3倍,它们的体积之和是52dm ,根据和倍问题规律解答。
【详解】52÷(1+3)
=52÷4
=13(dm )
13×3=39(dm )
故答案为:C
【点睛】和倍问题:和÷(倍数+1)=小数;小数×倍数=大数或者和-小数=大数。
12.B
【分析】由题意可知,第一个图形有1个点,第二个图形有5个点,第三个图形有9个点,以此类推第n个图形则有1+(n-1)×4个点。
【详解】由分析可知,第7个图形有:
1+(7-1)×4
=1+6×4
=1+24
=25(个)
所以,第7个图形有25个点。
故答案为:B
【点睛】要考查了学生通过特例分析从而归纳总结出一般结论的能力。对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解。
13. 6005000500 十亿 60
【分析】整数的写法:先写亿级,再写万级,最后写个级。哪个数位上一个单位也没有,就在那个数位上写0。“6”在十亿位,表示6个十亿。省略亿后面的尾数,要看千万位上的数,根据四舍五入法的原则,若千万位上的数字大于等于5,就向亿位进1;若千万位上的数字小于5,就舍去千万位及其后面数位上的数。
【详解】一个十位数,最高位是6,百万位和百位都是5,其他各数位上都是0,这个数写作6005000500,最高位上的“6”表示6个十亿,“四舍五入”到亿位约是60亿。
14. 3.5x 700
【分析】求一个数的几倍是多少,用乘法计算;当梨树有x棵时,那么苹果树有2.5x棵,将梨树和苹果树相加,可以得到果园里一共有果树多少棵;将x=200代入算式,计算出结果即可;据此解答。
【详解】根据分析:x+2.5x=(1+2.5)x=3.5x(棵),所以果园里一共有果树3.5x棵;3.5x=3.5×200=700(棵),所以当x为200时,果园里一共有700棵果树。
15.4
【分析】把80盒饼干分成3份,即(27,27,26),第一次称,天平两边各放27盒,如果天平不平衡,次品就在较轻的27盒中;如果天平平衡,次品在剩下的26盒中;
考虑最不利原则,次品在数量多的里面,把有次品的27盒饼干平均分成3份,即(9,9,9),第二次称,天平两边各放9盒,如果天平不平衡,次品就在较轻的9盒中;如果天平平衡,次品在剩下的9盒中;
再把有次品的9盒饼干平均分成3份,即(3,3,3),第三次称,天平两边各放3盒,如果天平不平衡,次品就在较轻的3盒中;如果天平平衡,次品就在剩下的3盒中;
最后把有次品的3盒饼干平均分成3份,即(1,1,1),第四次称,天平两边各放1盒,天平不平衡,次品就是较轻的那盒;如果天平平衡,次品就是剩下的那盒。
所以至少称4次能保证找出这盒饼干。
【详解】
假如用天平称,至少称4次能保证找出这盒饼干。
16.14
【分析】把四年级的作品数量看作单位“1”,五年级的作品数量是四年级的,求五年级作品数量,用四年级的作品数量×,求出五年级的作品数量;再把五年级的作品数量看作单位“1”,六年级的作品数量是五年级的,求六年级的作品数量,用五年级的作品数量×,即可求出六年级的作品数量,据此解答。
【详解】12××
=10×
=14(幅)
阳光小学举行绘画活动,四年级共制作12幅作品,五年级的作品数量是四年级的,六年级的作品数量是五年级的。六年级共制作14幅作品。
17.;;
【分析】甲数和乙数的比是4∶7,将甲数看作4,乙数看作7,甲数÷乙数=甲数占乙数的几分之几;甲乙两数差÷乙数=甲数比乙数少几分之几;甲乙两数差÷甲数=乙数比甲数多几分之几。
【详解】4÷7=
(7-4)÷7
=3÷7
=
(7-4)÷4
=3÷4
=
甲数和乙数的比是4∶7,则甲数占乙数的;甲数比乙数少,乙数比甲数多。
【点睛】关键是理解比的意义,求一个数占另一个数的几分之几用除法,差÷较大数=少几分之几,差÷较小数=多几分之几。
18.62.8
【分析】削成的最大的圆锥的底面直径等于正方体的棱长,高也等于正方体的棱长,那么,然后根据圆锥的体积公式解答即可。
【详解】用字母表示正方形的棱长,则。
(立方厘米)
当取近似值3.14时,(立方厘米)。
【点睛】本题考查了圆锥的体积公式的灵活应用,本题的关键是得到最大的圆锥的直径和高与正方体的关系。
19.60
【分析】把这批种子的总数量看作单位“1”,已知此批次种子出芽率为95%,则没出芽的数量占总数量的(1-95%),根据百分数除法的意义,用3÷(1-95%)即可求出总数量。
【详解】3÷(1-95%)
=3÷5%
=60(颗)
此次实验种子一共60颗。
20. n 2n+6
【分析】(1)第1个图形有1个,第2个图形有2个,第3个图形有3个,第4个图形有4个,……由此发现规律:第几个图形就有几个。
(2)每个图形最左侧有3个,最右侧有3个,3+3=6(个);第1个图形有2+6=8个,第2个图形有2×2+6=10个,第3个图形有2×3+6=12个,第4个图形有2×4+6=14个,……由此发现规律:第几个图形就有几个2加6个。
【详解】由发现的规律可知:第n个图形共有n个,(2n+6)个。
【点睛】在运用数形结合的方法探究数学规律时,一定要把图形和数一一对应。
21.见详解
【分析】(1)补全轴对称图形的方法:找出图形A的关键点,依据对称轴直线MN画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形B。
(2)根据旋转的特征,将图形B绕点O顺时针旋转90°,点B位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形C。
【详解】如图:
【点睛】此题主要考查补全轴对称图形以及图形的旋转,掌握其作图方法是解题的关键。
22.够
【分析】根据长方形面积=长×宽,求出图书室面积,图书室面积÷瓷砖面积=需要的瓷砖块数,结果用进一法保留近似数,比较即可。
【详解】
(块)
答:100块够。
【点睛】关键是掌握小数乘除法的计算方法,理解用进一法保留近似数的实际意义。
23.12.8克;8克
【分析】求一个数的几倍是多少用乘法,设每平方米夹竹桃叶能吸附灰尘x克,则每平方米榆树叶能吸附灰尘1.6x克,根据每平方米榆树叶能吸附灰尘质量-每平方米夹竹桃叶能吸附灰尘质量=4.8克,列出方程求出x的值,是每平方米夹竹桃叶能吸附灰尘质量,每平方米夹竹桃叶能吸附灰尘质量×1.6=每平方米榆树叶能吸附灰尘质量。
【详解】解:设每平方米夹竹桃叶能吸附灰尘x克。
1.6x-x=4.8
0.6x=4.8
0.6x÷0.6=4.8÷0.6
x=8
8×1.6=12.8(克)
答:每平方米榆树叶和夹竹桃叶分别能吸附灰尘12.8克、8克。
24.20万亿美元
【分析】把美国2019年GDP看作单位“1”,根据百分数除法的意义,用14÷70%即可求出2019年美国的GDP。
【详解】14÷70%=20(万亿美元)
答:2019年美国的GDP大约是20万亿美元。
25.140人
【分析】七年级学生分三组参加,第一组与第二组人数的比是5∶4,第二组和第三组人数的比是3∶2,可知一、二、三组的人数比是15∶12∶8,根据比与分数的关系可知:第一小组占总人数的,第二、三小组占总人数的,第一小组比第二与三组人数总和少20人,用第二、三组占的总数的几分之几减去第一组占总人数的几分之几,就是20对应的分率,据此解答。
【详解】20÷(-)
=20÷(-)
=20÷
=140(人)
答:七年级参加植树的共有140人。
【点睛】本题的关键是先求出三个班人数的比,然后求出20对应的分率,再根据分数除法的意义列式解答。
26.1526.04立方厘米
【分析】圆锥型的底面周长即圆的周长,根据圆的周长=求出圆的半径,圆的高与圆的直径相同,即h=2r,根据圆锥的体积=,求出生日帽的体积。
【详解】56.52÷(3.14×2)
=56.52÷6.28
=9(厘米)
9×2=18(厘米)
答:这个生日帽的体积是1526.04立方厘米。
27.(1)600人
(2)30人
(3)增加学生体育锻炼的时间,适当增加锻炼的强度
【分析】(1)把六年级的总人数看作单位“1”,用达到优秀的人数除以对应分率等于六年级参加本次测试的总人数。
(2)把六年级的总人数看作单位“1”,用单位“1”减去优秀、及格、良好人数所占的分率,求出不及格人数所占的分率,再用六年级参加本次测试的总人数乘不及格人数对应的分率即可解答。
(3)根据这次测试结果给出合理建议即可。
【详解】(1)90÷15%=600(人)
答:六年级参加本次测试的学生一共有600人。
(2)1-30%-50%-15%
=70%-50%-15%
=20%-15%
=5%
600×5%=30(人)
答:六年级不及格的学生有30人。
(3)如果我是该校校长,增加学生体育锻炼的时间,适当增加锻炼的强度。(答案不唯一)
【点睛】利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数相关解题思路解答即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
