六年级下册数学人教版图形的认识与测量(课件)(共25张PPT)
文档属性
| 名称 | 六年级下册数学人教版图形的认识与测量(课件)(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 960.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-05 00:00:00 | ||
图片预览



文档简介
(共25张PPT)
整理与复习
——图形的认识与测量
第3课时 立体图形的认识与测量
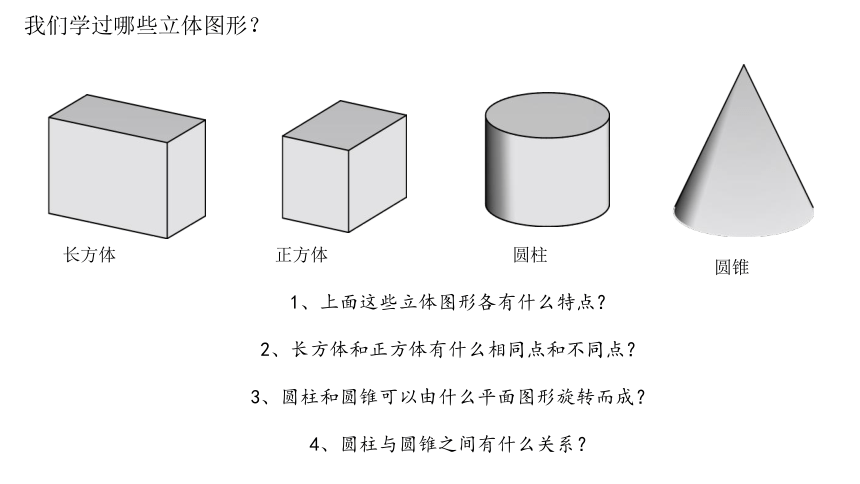
我们学过哪些立体图形?
长方体
正方体
圆柱
圆锥
1、上面这些立体图形各有什么特点?
2、长方体和正方体有什么相同点和不同点?
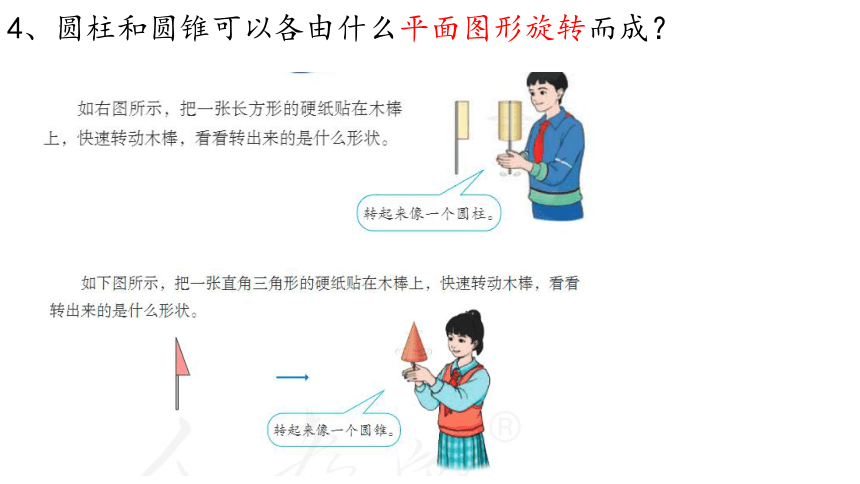
3、圆柱和圆锥可以由什么平面图形旋转而成?
4、圆柱与圆锥之间有什么关系?
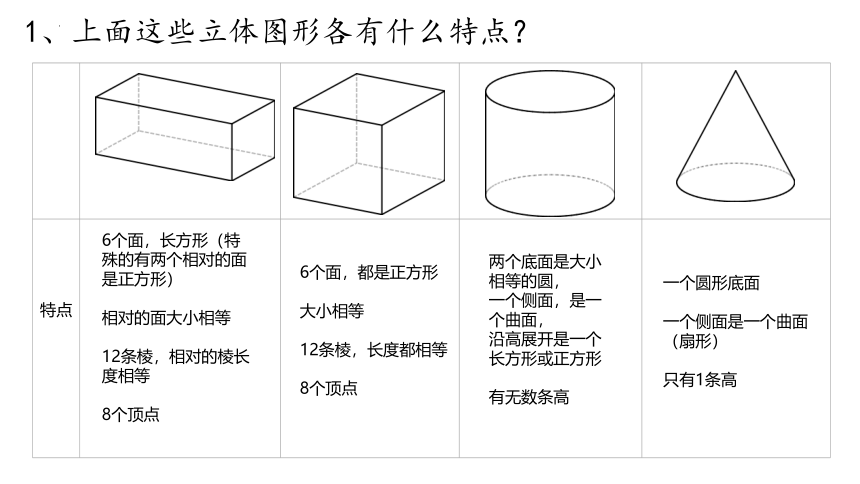
1、上面这些立体图形各有什么特点?
特点
6个面,长方形(特殊的有两个相对的面是正方形)
相对的面大小相等
12条棱,相对的棱长度相等
8个顶点
6个面,都是正方形
大小相等
12条棱,长度都相等
8个顶点
两个底面是大小相等的圆,
一个侧面,是一个曲面,
沿高展开是一个长方形或正方形
有无数条高
一个圆形底面
一个侧面是一个曲面
(扇形)
只有1条高
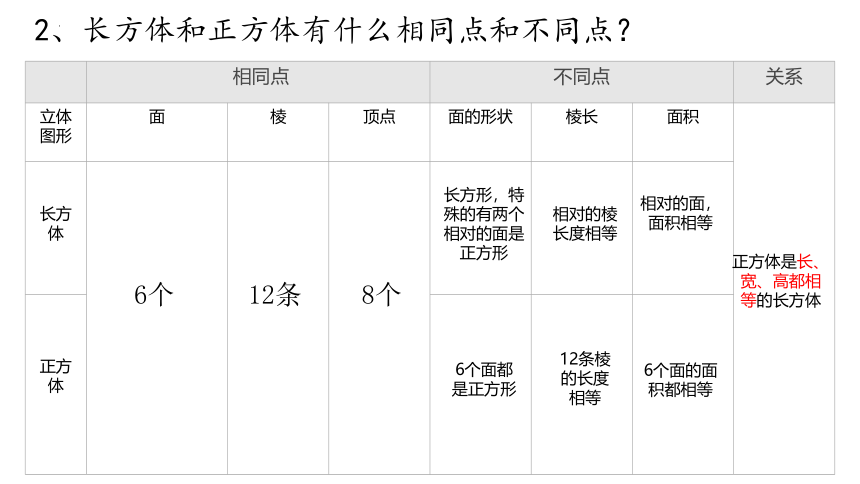
2、长方体和正方体有什么相同点和不同点?
相同点 不同点 关系
立体图形 面 棱 顶点 面的形状 棱长 面积
长方体 正方体 6个
12条
8个
长方形,特殊的有两个相对的面是正方形
相对的棱
长度相等
相对的面,面积相等
6个面都是正方形
12条棱的长度相等
6个面的面积都相等
正方体是长、宽、高都相等的长方体
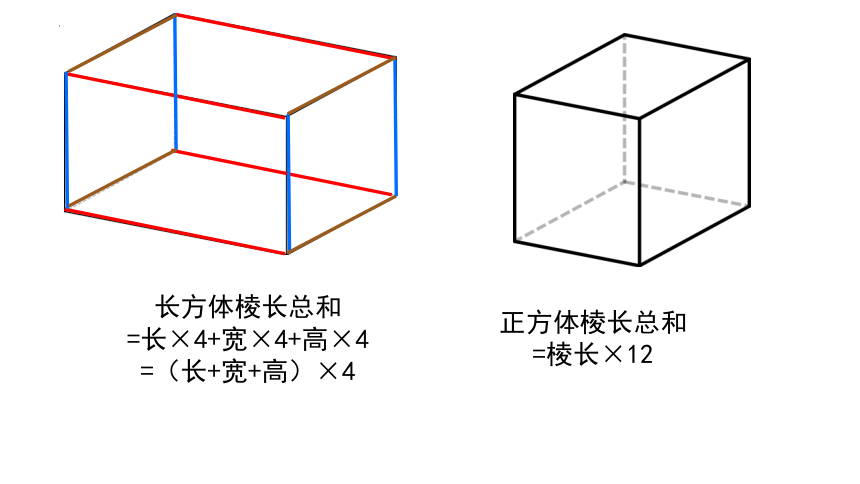
长方体棱长总和
=长×4+宽×4+高×4
=(长+宽+高)×4
正方体棱长总和
=棱长×12
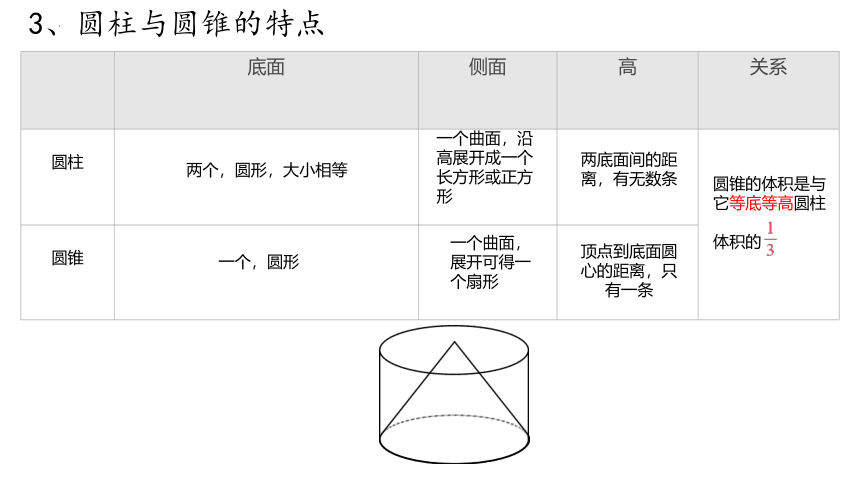
3、圆柱与圆锥的特点
底面 侧面 高 关系
圆柱
圆锥 两个,圆形,大小相等
一个,圆形
一个曲面,沿高展开成一个长方形或正方形
两底面间的距 离,有无数条
一个曲面,展开可得一个扇形
顶点到底面圆心的距离,只有一条
圆锥的体积是与它等底等高圆柱
体积的
4、圆柱和圆锥可以各由什么平面图形旋转而成?
5、常见立体图形的表面积和体积计算公式
·立体图形的表面积:
围成立体图形所有面的面积总和,
常用面积单位: 平方米(m2)
平方分米(dm2)
平方厘米(cm2)
·长方体和正方体展开图
长
宽
高
棱长
后
上
前
下
左
右
前后:长×高×2
上下:长×宽×2
左右:宽×高×2
表面积=前后+上下+左右
表面积=一个正方形面的面积×6
根据展开图,如何判断
这个展开图可以组成正方体?
·圆柱的展开图
一个侧面:长方形或正方形
两个底面:大小相等的圆
长方形的长=圆柱底面周长,
长方形的宽=圆柱的高
当侧面展开图是个正方形时,
说明圆柱底面周长=圆柱的高
圆柱侧面积=
底面周长×高
底面面积=圆的面积,2个底面即2S底
圆柱的表面积=S侧+2S底
·体积:物体所占空间的大小叫做物体的体积
计量体积要用体积单位,
常用体积单位有:
立方厘米(cm3)
立方分米(dm3)
立方米(m3)
a
b
c
1
1
1
长方体的体积=长×宽×高
底面积
单位体积的个数
正方体的体积=棱长×棱长×棱长
底面积
正方体是特殊的长方体
圆柱的体积
=近似长方体的体积
=长×宽×高
=底面周长的一半×半径×高
=πr×r×h
体积不变,
表面积增加了左右两个面
即半径×高×2
转化思想
实验法
把圆柱倒满水,
再往与圆柱等底等高的圆锥里倒,
正好倒了三次。
等
底
等
高
立体图形 表面积计算公式 体积计算公式
a
b
h
a
a
a
h
r
r
h
S=2(ab+ah+bh)
V=abh
S=6a2
V=a3
S表=S侧+2S底
=Ch+2πr2
=πdh+2πr2
=2πrh+2πr2
V=πr2h
V=Sh
V= πr2h
V= Sh
6、容积
指箱子、油桶、仓库等容器所能容纳物体的体积,
通常叫做它们的容积。
温馨提示:
长方体、正方体、圆柱或圆锥容器的容积的计算方法,
跟体积的计算方法相同,但要从容器里面量长宽高或底面半径
常用容积单位升(L)和毫升(mL)
1L=1dm3
1mL=1cm3
1L=1000mL
外部&内部
7、求不规则物体的体积
怎样量出一个马铃薯的体积?
1、将一个马铃薯完全浸没在一个装有300 mL 的量杯里,
此时水面上升至450 mL 的刻度处,这个马铃薯的体积是多少?
2、将一个马铃薯完全浸没在一个装有水的圆柱形容器里,水面上升32cm(没有溢出),
已知这个圆柱形容器的内半径为10㎝,如何求这个马铃薯的体积?
3、从里面量出长方体的长、宽、高,
分别量出放入马铃薯(浸没)前后的水的高度,
通过求出上升部分的水的体积,
就是这个马铃薯的体积。
排水法
求不规则物体的体积:
将物体全部浸没在水里,上升部分的水的体积就是物体的体积。
不规则物体的体积=容器的底面积×水面上升的高度
一个高30厘米的酒瓶中盛有酒,如果把它倒置在桌面上(如图所示),
酒瓶的容积是多少?
这个瓶子不是一个完整的圆柱,
无法直接计算容积。
把瓶子的容积转化成了
两个圆柱的体积。
利用体积不变的特性,
把不规则图形转化成规则图形来计算。
7、观察物体
在方格纸上分别画出从不同方向看到左边立体图形的形状图。
正面看
正面
左面
上面
三视图
孙老师用几个1立方厘米的正方体木块摆了一个物体,如图是从不同方向看到的图形。这个物体的表面积是( )平方厘米,体积是( )立方厘米。
上面
前面
左面
谢谢观看
整理与复习
——图形的认识与测量
第3课时 立体图形的认识与测量
我们学过哪些立体图形?
长方体
正方体
圆柱
圆锥
1、上面这些立体图形各有什么特点?
2、长方体和正方体有什么相同点和不同点?
3、圆柱和圆锥可以由什么平面图形旋转而成?
4、圆柱与圆锥之间有什么关系?
1、上面这些立体图形各有什么特点?
特点
6个面,长方形(特殊的有两个相对的面是正方形)
相对的面大小相等
12条棱,相对的棱长度相等
8个顶点
6个面,都是正方形
大小相等
12条棱,长度都相等
8个顶点
两个底面是大小相等的圆,
一个侧面,是一个曲面,
沿高展开是一个长方形或正方形
有无数条高
一个圆形底面
一个侧面是一个曲面
(扇形)
只有1条高
2、长方体和正方体有什么相同点和不同点?
相同点 不同点 关系
立体图形 面 棱 顶点 面的形状 棱长 面积
长方体 正方体 6个
12条
8个
长方形,特殊的有两个相对的面是正方形
相对的棱
长度相等
相对的面,面积相等
6个面都是正方形
12条棱的长度相等
6个面的面积都相等
正方体是长、宽、高都相等的长方体
长方体棱长总和
=长×4+宽×4+高×4
=(长+宽+高)×4
正方体棱长总和
=棱长×12
3、圆柱与圆锥的特点
底面 侧面 高 关系
圆柱
圆锥 两个,圆形,大小相等
一个,圆形
一个曲面,沿高展开成一个长方形或正方形
两底面间的距 离,有无数条
一个曲面,展开可得一个扇形
顶点到底面圆心的距离,只有一条
圆锥的体积是与它等底等高圆柱
体积的
4、圆柱和圆锥可以各由什么平面图形旋转而成?
5、常见立体图形的表面积和体积计算公式
·立体图形的表面积:
围成立体图形所有面的面积总和,
常用面积单位: 平方米(m2)
平方分米(dm2)
平方厘米(cm2)
·长方体和正方体展开图
长
宽
高
棱长
后
上
前
下
左
右
前后:长×高×2
上下:长×宽×2
左右:宽×高×2
表面积=前后+上下+左右
表面积=一个正方形面的面积×6
根据展开图,如何判断
这个展开图可以组成正方体?
·圆柱的展开图
一个侧面:长方形或正方形
两个底面:大小相等的圆
长方形的长=圆柱底面周长,
长方形的宽=圆柱的高
当侧面展开图是个正方形时,
说明圆柱底面周长=圆柱的高
圆柱侧面积=
底面周长×高
底面面积=圆的面积,2个底面即2S底
圆柱的表面积=S侧+2S底
·体积:物体所占空间的大小叫做物体的体积
计量体积要用体积单位,
常用体积单位有:
立方厘米(cm3)
立方分米(dm3)
立方米(m3)
a
b
c
1
1
1
长方体的体积=长×宽×高
底面积
单位体积的个数
正方体的体积=棱长×棱长×棱长
底面积
正方体是特殊的长方体
圆柱的体积
=近似长方体的体积
=长×宽×高
=底面周长的一半×半径×高
=πr×r×h
体积不变,
表面积增加了左右两个面
即半径×高×2
转化思想
实验法
把圆柱倒满水,
再往与圆柱等底等高的圆锥里倒,
正好倒了三次。
等
底
等
高
立体图形 表面积计算公式 体积计算公式
a
b
h
a
a
a
h
r
r
h
S=2(ab+ah+bh)
V=abh
S=6a2
V=a3
S表=S侧+2S底
=Ch+2πr2
=πdh+2πr2
=2πrh+2πr2
V=πr2h
V=Sh
V= πr2h
V= Sh
6、容积
指箱子、油桶、仓库等容器所能容纳物体的体积,
通常叫做它们的容积。
温馨提示:
长方体、正方体、圆柱或圆锥容器的容积的计算方法,
跟体积的计算方法相同,但要从容器里面量长宽高或底面半径
常用容积单位升(L)和毫升(mL)
1L=1dm3
1mL=1cm3
1L=1000mL
外部&内部
7、求不规则物体的体积
怎样量出一个马铃薯的体积?
1、将一个马铃薯完全浸没在一个装有300 mL 的量杯里,
此时水面上升至450 mL 的刻度处,这个马铃薯的体积是多少?
2、将一个马铃薯完全浸没在一个装有水的圆柱形容器里,水面上升32cm(没有溢出),
已知这个圆柱形容器的内半径为10㎝,如何求这个马铃薯的体积?
3、从里面量出长方体的长、宽、高,
分别量出放入马铃薯(浸没)前后的水的高度,
通过求出上升部分的水的体积,
就是这个马铃薯的体积。
排水法
求不规则物体的体积:
将物体全部浸没在水里,上升部分的水的体积就是物体的体积。
不规则物体的体积=容器的底面积×水面上升的高度
一个高30厘米的酒瓶中盛有酒,如果把它倒置在桌面上(如图所示),
酒瓶的容积是多少?
这个瓶子不是一个完整的圆柱,
无法直接计算容积。
把瓶子的容积转化成了
两个圆柱的体积。
利用体积不变的特性,
把不规则图形转化成规则图形来计算。
7、观察物体
在方格纸上分别画出从不同方向看到左边立体图形的形状图。
正面看
正面
左面
上面
三视图
孙老师用几个1立方厘米的正方体木块摆了一个物体,如图是从不同方向看到的图形。这个物体的表面积是( )平方厘米,体积是( )立方厘米。
上面
前面
左面
谢谢观看
