沪科版九年级数学上册 第23章《解直角三角形》单元测试卷(含详解)
文档属性
| 名称 | 沪科版九年级数学上册 第23章《解直角三角形》单元测试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-05 13:32:57 | ||
图片预览




文档简介
第23章《解直角三角形》单元测试卷
一、单选题(本大题共10小题,每小题3分,共30分)
1.下列运算正确的是( )
A. B.
C. D.
2.如图,一个钟摆的摆长为米,当钟摆向两边摆动时,摆角为,且两边的摆动角度相同,则它摆至最高位置与其摆至最低位置时的高度之差为( )
A.米 B.米
C.米 D.米
3.如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C在OB上,,连接AC,过点O作交AC的延长线于P.若,则的值是( )
A. B. C. D.3
4.如图,在边长为1的的正方形网格中,为与正方形网格线的交点,下列结论中不正确的是( )
A. B. C. D.
5.综合与实践课上,李老师让同学们以矩形纸片的折叠为主题开展数学活动.如图,将矩形纸片对折,折痕为,再把点A折叠在折痕上,其对应点为,折痕为,连接,若,,则的值为( )
A. B. C. D.
6.中国最早的一部数学著作《周髀算经》中记载着勾股定理,约1400年后的汉代数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的证明.这就是如图所示的“赵爽弦图”,若,则小正方形与直角三角形的面积比为( )
A. B.1:1 C. D.1:5
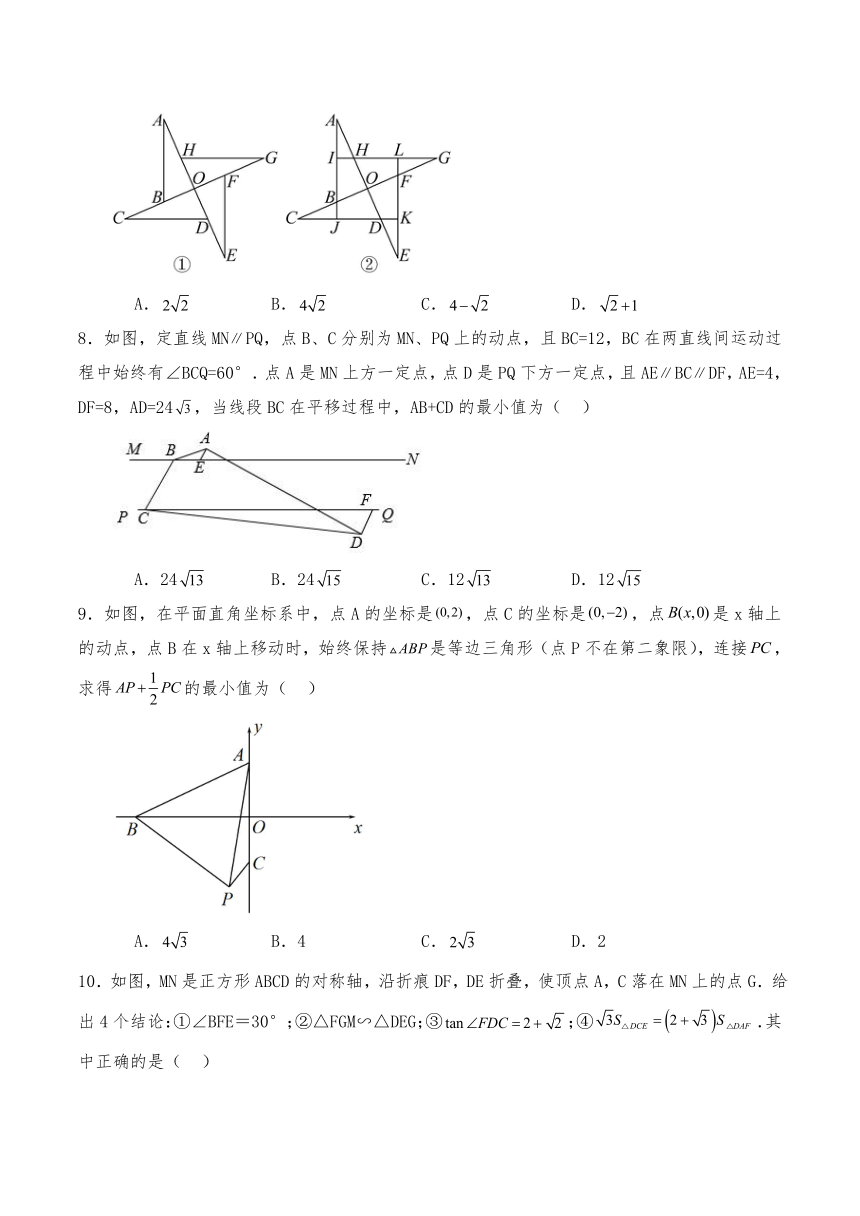
7.任意一张正方形先对折再翻折然后加上废旧的草杆就能做成一个简易的纸风车,迎着风就会哗啦啦转动起来,小小的纸风车带来童年满满的回忆.如图是彤彤折叠的一个纸风车,风车由四个全等的直角三角形组成,其中∠DOG 为90°.延长直角三角形的斜边,恰好交于四个直角三角形的斜边中点,若,那么这个风车的面积为( )
A. B. C. D.
8.如图,定直线MNPQ,点B、C分别为MN、PQ上的动点,且BC=12,BC在两直线间运动过程中始终有∠BCQ=60°.点A是MN上方一定点,点D是PQ下方一定点,且AEBCDF,AE=4,DF=8,AD=24,当线段BC在平移过程中,AB+CD的最小值为( )
A.24 B.24 C.12 D.12
9.如图,在平面直角坐标系中,点A的坐标是,点C的坐标是,点是x轴上的动点,点B在x轴上移动时,始终保持是等边三角形(点P不在第二象限),连接,求得的最小值为( )
A. B.4 C. D.2
10.如图,MN是正方形ABCD的对称轴,沿折痕DF,DE折叠,使顶点A,C落在MN上的点G.给出4个结论:①∠BFE=30°;②△FGM∽△DEG;③;④.其中正确的是( )
A.①②③ B.②③④ C.①③④ D.①②④
二、填空题(本大题共8小题,每小题4分,共32分)
11.若,则 .
12.如图,平面内几条线段满足.AB、CD的交点为E,现测得,,,则CD的长度为 .
13.如图,中,,以为轴,轴经过点,建立平面直角坐标系,已知,,将沿着轴翻折,的对应点为,若抛物线 ,恰好过、、,则
14.在平面直角坐标系中,已知,,点是直线上的一点,连接、.当在一定范围内取值时,直线上总存在点,使得,则此时的取值范围为 .
15.如图,菱形绕A点顺时针旋转,B、C、D的对应点分别为、、,若和D重合,菱形面积为,则阴影的面积= .
16.如图,现有一矩形纸片,为矩形的对角线,,,点为上一点,沿线段将折叠为,交于点,连接,作点关于线段对称的点,点恰好落在对角线上,连接,.则的大小为 ;的长为 .
17.如图,三角形中,于,以为边作菱形,使点落在边上,点在上,交于点,若,,则的长为 .
18.如图,在平面直角坐标系中,的顶点A在直线上,顶点B在x轴上,垂直轴,且,顶点在直线上,;过点作直线的垂线,垂足为,交x轴于,过点作垂直x轴,交于点,连接,得到第一个;过点作直线的垂线,垂足为,交x轴于,过点作垂直x轴,交于点,连接,得到第二个;如此下去,……,则的面积是 .
三、解答题(本大题共6小题,共58分)
19.(8分)计算下列的三角函数值(写出计算过程,保留计算结果):
.
20.(8分)如图所示,,上有一点,,,
(1)用含的表达式表示出AC的长度
(2)用含的表达式表示出点D到AC的距离
21.(10分)如图.△ABC中.AB=BC=.AC=4.D为AC的中点.E、F分别为AD、CD上的动点.过E作PE⊥AD.且DE+2PE=2.连接PF.
(1)求sin∠C;
(2)连接AP.
①求证AP∥BC;
②请直接写出PF+CF的最大值.
22.(10分)如图,计划在山顶A的正下方沿直线CD方向开通穿山隧道EF.在点E处测得山顶A的仰角为45°,在距E点80m的C处测得山顶A的仰角为30°,从与F点相距10m的D处测得山顶A的仰角为45°,点C、E、F、D在同一直线上,求隧道EF的长度.
23.(10分)圣·索菲亚教堂坐落于中国黑龙江省,是一座始建于1907年拜占庭风格的东正教教堂,被列为第四批全国重点文物保护单位,其中央主体建筑集球、圆柱、棱柱于一体,极具对称之美,可以让游客从任何角度都能领略它的美,如图,小明为了估算索菲亚教堂的高度,在索菲亚教堂的正东方向找到一座建筑物,高为6m,在它们之间的地面上的点M(B,M,D三点共线)处测得建筑物顶A,教堂顶C的仰角分别是15°和60°,在楼顶A处测得教堂顶C的仰角为30°,那么小明计算索菲亚教堂的高度为多少? (保留根号,,,)
24.(12分)(2022·河北石家庄·校联考三模)小明在一段斜坡上进行跑步训练.在训练过程中,始终有一架无人机在小明正上方随他一起运动,无人机速度为,距水平地面的高度总为(在直线上运动)现就小明训练中部分路段作出如图函数图象:已知,斜坡的坡度:,斜坡的坡角为.
(1)点坐标为______,段关于的函数解析式为______;
(2)小明在斜坡上的跑步速度是______,并求段关于的函数解析式;
(3)若小明沿方向运动,求无人机与小明之间距离不超过10m的时长.(参考数据:,,)
答案
1.D
【分析】根据锐角三角函数值的计算,以及二次根式的运算,逐一进行判断即可.
解:A、,选项错误,不符合题意;
B、,选项错误,不符合题意;
C、,选项错误,不符合题意;
D、,选项正确,符合题意.
故选D.
2.A
【分析】由题可知,秋千摆到最低点时,点为弧的中心 ,由垂径定理知,.再根据锐角三角函数解三角形求得即可.
解:∵点为弧的中点,为圆心,
由垂径定理知,,,
∵,
∴,
∵,
在中,由三角函数可得,
∴,
故选:A.
3.C
【分析】由可知,OP与x轴的夹角为45°,又因为,则为等腰直角形,设OC=x,OB=2x,用勾股定理求其他线段进而求解.
解:∵P点坐标为(1,1),
则OP与x轴正方向的夹角为45°,
又∵,
则∠BAO=45°,为等腰直角形,
∴OA=OB,
设OC=x,则OB=2OC=2x,
则OB=OA=3x,
∴.
4.C
【分析】由勾股定理分别算出三边的长度,再利用勾股定理逆定理证明是直角三角形,再根据锐角三角函数进行求解,通过证明继而进行判断即可.
解:由题意得,,
,
是直角三角形,,故B正确,不符合题意;
,故A正确,不符合题意;
,
,
,
,
,
,
,故C错误,符合题意;
,故D正确,不符合题意;
故选:C.
5.A
【分析】先证明,,,,,可得,,再利用正切的定义求解即可.
解:∵矩形纸片对折,折痕为,,,
∴,,,,
由折叠可得:,
∴,
∴,
∴.
故选A
6.B
【分析】在中,根据锐角三角函数的定义得出,代入,两边平方得出,由“赵爽弦图”,结合图形可知等于小正方形的边长,那么.再根据,即可求解.
解:如图.
在中,∵,
∴.
∵,
∴,
∴,
即.
设,则,
∴,
∴.
故选:B.
7.A
【分析】连接由题意可得,进而说明为等腰直角三角形,再说明垂直平分、垂直平分,进而说明,然后再运用解直角三角形求得,然后再求得三角形的面积,最后求风车面积即可.
解:如图:连接
由题意可得:
,
为等腰直角三角形
又 :
,
,即
又
垂直平分
同理:垂直平分
是等腰三角形顶角的角平分线
即
由题意可得
又,
,
在中,,
,
设,即
,
,
设(),,
,即,
,
又,
,
,
.
故选A.
8.C
【分析】如图所示,过点F作交BC于H,连接EH,可证明四边形CDFH是平行四边形,得到CH=DF=8,CD=FH,则BH=4,从而可证四边形ABHE是平行四边形,得到AB=HE,即可推出当E、F、H三点共线时,EH+HF有最小值EF即AB+CD有最小值EF,延长AE交PQ于G,过点E作ET⊥PQ于T,过点A作AL⊥PQ于L,过点D作DK⊥PQ于K,证明四边形BEGC是平行四边形,∠EGT=∠BCQ=60°,得到EG=BC=12,然后通过勾股定理和解直角三角形求出ET和TF的长即可得到答案.
解:如图所示,过点F作交BC于H,连接EH,
∵,
∴四边形CDFH是平行四边形,
∴CH=DF=8,CD=FH,
∴BH=4,
∴BH=AE=4,
又∵,
∴四边形ABHE是平行四边形,
∴AB=HE,
∵,
∴当E、F、H三点共线时,EH+HF有最小值EF即AB+CD有最小值EF,
延长AE交PQ于G,过点E作ET⊥PQ于T,过点A作AL⊥PQ于L,过点D作DK⊥PQ于K,
∵,
∴四边形BEGC是平行四边形,∠EGT=∠BCQ=60°,
∴EG=BC=12,
∴,
同理可求得,,
∴,
∵AL⊥PQ,DK⊥PQ,
∴,
∴△ALO∽△DKO,
∴,
∴,
∴,
∴,
∴,
故选C.
9.C
【分析】如图1所示,以OA为边,向右作等边△AOD,连接PD,过点D作DE⊥OA于E,先求出点D的坐标,然后证明△BAO≌△PAD得到∠PDA=∠BOA=90°,则点P在经过点D且与AD垂直的直线上运动,当点P运动到y轴时,如图2所示,证明此时点P的坐标为(0,-2)从而求出直线PD的解析式;如图3所示,作点A关于直线PD的对称点G,连接PG,过点P作PF⊥y轴于F,设直线PD与x轴的交点为H,先求出点H的坐标,然后证明∠HCO=30°,从而得到,则当G、P、F三点共线时,有最小值,即有最小值,再根据轴对称的性质求出点G在x轴上,则OG即为所求.
解:如图1所示,以OA为边,向右作等边△AOD,连接PD,过点D作DE⊥OA于E,
∵点A的坐标为(0,2),
∴OA=OD=2,
∴OE=AE=1,
∴,
∴点D的坐标为;
∵△ABP是等边三角形,△AOD是等边三角形,
∴AB=AP,∠BAP=60°,AO=AD,∠OAD=60°,
∴∠BAP+∠PAO=∠DAO+∠PAO,即∠BAO=∠PAD,
∴△BAO≌△PAD(SAS),
∴∠PDA=∠BOA=90°,
∴点P在经过点D且与AD垂直的直线上运动,
当点P运动到y轴时,如图2所示,此时点P与点C重合,
∵△ABP是等边三角形,BO⊥AP,
∴AO=PO=2,
∴此时点P的坐标为(0,-2),
设直线PD的解析式为,
∴,
∴,
∴直线PD的解析式为;
如图3所示,作点A关于直线PD的对称点G,连接PG,过点P作PF⊥y轴于F,连接CG,设直线PD与x轴的交点为H,
∴点H的坐标为,
∴,
∴∠OCH=30°,
∴,
由轴对称的性质可知AP=GP,
∴,
∴当G、P、F三点共线时,有最小值,即有最小值,
∵A、G两点关于直线PD对称,且∠ADC=90°,
∴AD=GD,即点D为AG的中点,
∵点A的坐标为(0,2),点D的坐标为,
∴AG=2AD=2OA=4,
∵AC=4,∠CAG=60°,
∴△ACG是等边三角形,
∵OC=OA,
∴OG⊥AC,即点G在x轴上,
∴由勾股定理得,
∴当点P运动到H点时,有最小值,即有最小值,最小值即为OG的长,
∴的最小值为,
故选:C.
10.D
【分析】设,根据折叠的性质得,,根据轴对称的性质得出,即可判断①,从而得出,,继而判断②,设,则,解,即可判断③,分别求得即可判断④.
解:设,根据折叠的性质得,,
四边形是正方形,则,
,
设正方形的边长为,则,
MN是正方形ABCD的对称轴,
,
,
,
,
,
,故①正确,
,
,,
,,
△FGM∽△DEG;故②正确,
设,则,
在中,,
,
解得,
即,
,
故③不正确;
,
,
,
,
,
,
故④正确
故①②④正确,
故选D.
二、填空题
11.
【分析】根据锐角三角函数的增减性判断出与的大小、与 的大小,然后化简计算即可.
解:∵,
∴.
∴
,
故答案为:.
12.
【分析】延长交于,过作交于,根据“字形”可知,得到相似比,设,在中,根据勾股定理得,结合条件得出,再利用相似比即可求出的长度.
解:延长交于,过作交于,如图所示:
,
,
,
,
,
,
,
,
,,
,
设,则,
在中,根据勾股定理得,
,解得,
,解得,
故答案为:.
13.
【分析】根据题意得出,进而根据正切的定义,得出的坐标,进而求得点的坐标,根据轴对称的性质求得的坐标,待定系数法求得解析式,进而化为顶点式,即可求解.
解:∵中,,,
∴,
∴,
∵,
∴,设,则,
则,
∵,
∴,
即,,
∵,
∴,即,
∵将沿着轴翻折,的对应点为,
∴,
设抛物线解析式为,将点代入得,
解得:
∴抛物线解析式为
故答案为:.
14.且
【分析】先确定点,点的位置,并连接,过点作轴于,交轴于,作关于的对称点,连接,过点作交轴于,过点作交轴于,解出所在直线的解析式,再证明,由此解出直线,直线的解析式,由此即可求解.
解:根据题意,在平面直角坐标系中标出点,点,连接,作图如下,过点作轴于,交轴于,作关于的对称点,连接,过点作交轴于,过点作交轴于,则,直线和直线是符合条件的直线,理由如下,
设过点,点的直线方程为,
∴,解得,,
∴所在直线的解析式为,
∵,
∴直线,直线是符合条件的直线,
∵,,轴,
∴,
∴,
在中,,且,
∴,则,
∵,
∴,且,
∴,
∴,把代入得,,
∵点与点关于对称,
∴,,
∵,
∴,,
∴是等边三角形,
∴,则,
∴,把代入得,
∵点不能与点重合,
∴,
∴的取值范围为且.
15.
【分析】如图,过作交的延长线于,过作于,由旋转的性质可得:,可得,由菱形面积求解,证明,,可得,,,可得,从而可得答案.
解:如图,过作交的延长线于,过作于,
由旋转的性质可得:,
∴,
∵菱形面积为,
∴,
解得:,
由菱形的性质可得:,,
∴,
∴,
∴,
∴,
∴;
故答案为:.
16. 75
【分析】证明,可得;再证明,,求出,可得结论.
解:由折叠的性质可知,,
,关于对称,
,
,
,
,
,
,
.
,,,
,
,,
,,
,
,,
,.
故答案为:75;.
17.6
【分析】菱形的性质得到,推出,外角的性质,得到,进而得到,过点作于点,推出,利用锐角三角函数和勾股定理求出的长即可.
解:∵四边形为菱形,
∴,
∴,
∵,
∴,
过点作于点,设交于点,则,
∵,且,
∴,
∵,
∴,
∵,
∴,
在中,,
设,则:,
∴,
∴;
故答案为:.
18.
【分析】解直角三角形得出,,求出,证明,,得出,,总结得出,从而得出.
解:∵,
∴,
∵轴,
∴点A的横坐标为,
∵,
∴点A的纵坐标为,
∴,
∴,
∵,
∴设,则,
∴,
∴,
∴,
,
∵,
∴,
∴平分,
∵,,
∴,
∵,,
∴,
∴,
∴,
∴
,
∵,
∴,
∴,
∵,,,
∴,
∴,
∴,
∴,,
∵轴,轴,
∴,,
∵轴,轴,轴,
∴,
∴,,
∵,
∴,,
∴,
∵,
∴,
同理,
∴,
,
∴,
∴.
故答案为:.
三、解答题
19.
解:
20.
(1)解:在中,,,,
∴,
在中,,,
∴;
(2)解:在中,,,
∴,
则,
设点D到AC的距离为h,
由得
.
21.
(1)解:连接BD,如下图,
∵,
∴是等腰三角形.
∵D为AC的中点,
∴.
∵,
∴,
∴,
∴;
(2)解:①∵,
设,
则,
∴.
∵由(1)得,,
∴,
∴.
∵,
∴,
∴,
∴,
∴;
②由①,,PE⊥AD,
∴.
∵E、F分别为AD、CD上的动点,使为中点,
则,,
∴.
∵ ,且,x不能小于0,
∴,
解得,
∴,
∴当时,有最大值,最大值是.
22.
解:过点A作AG⊥CD于点G,如图所示:
由题意得:,
∴△EAD是等腰直角三角形,
∴AG=EG=DG,
设AG=EG=DG=x,
∴,
∴,
解得:,
∴,
∴;
答:隧道EF的长度米.
23.
解:如图,过作于,则四边形是矩形,
∴,,
∵,
∴,
设,则,,
∴,,
∵,
∴,
∴,
解得:,
∴,
∴索菲亚教堂的高度为米.
24.
(1)解:如图,过A点作于点,
,
,
,斜坡的坡度::,
,,
点A坐标为,
设段关于的函数解析式为,
代入,,
解得:,
段关于的函数解析式
,
故答案为:;.
(2)解:在中,,,
,
,
,,
在训练过程中,始终有一架无人机在小明正上方随他一起运动.无人机速度为,
小明在斜坡上跑步的时间为:,
小明在斜坡上的跑步速度是:,
,,
,
,
设段关于的函数解析式为:代入,,
得:,
解得:,
段关于的函数解析式为;
故答案为:.
(3)解:在段上无人机与小明之间的距离为时,
则有:,
解得:,
无人机飞行的时间为;
在段上,无人机与小明之间距离为时,则有:,
解得:,
无人机飞行的时间为,
无人机与小明之间距离不超过的时长为:.
一、单选题(本大题共10小题,每小题3分,共30分)
1.下列运算正确的是( )
A. B.
C. D.
2.如图,一个钟摆的摆长为米,当钟摆向两边摆动时,摆角为,且两边的摆动角度相同,则它摆至最高位置与其摆至最低位置时的高度之差为( )
A.米 B.米
C.米 D.米
3.如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C在OB上,,连接AC,过点O作交AC的延长线于P.若,则的值是( )
A. B. C. D.3
4.如图,在边长为1的的正方形网格中,为与正方形网格线的交点,下列结论中不正确的是( )
A. B. C. D.
5.综合与实践课上,李老师让同学们以矩形纸片的折叠为主题开展数学活动.如图,将矩形纸片对折,折痕为,再把点A折叠在折痕上,其对应点为,折痕为,连接,若,,则的值为( )
A. B. C. D.
6.中国最早的一部数学著作《周髀算经》中记载着勾股定理,约1400年后的汉代数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的证明.这就是如图所示的“赵爽弦图”,若,则小正方形与直角三角形的面积比为( )
A. B.1:1 C. D.1:5
7.任意一张正方形先对折再翻折然后加上废旧的草杆就能做成一个简易的纸风车,迎着风就会哗啦啦转动起来,小小的纸风车带来童年满满的回忆.如图是彤彤折叠的一个纸风车,风车由四个全等的直角三角形组成,其中∠DOG 为90°.延长直角三角形的斜边,恰好交于四个直角三角形的斜边中点,若,那么这个风车的面积为( )
A. B. C. D.
8.如图,定直线MNPQ,点B、C分别为MN、PQ上的动点,且BC=12,BC在两直线间运动过程中始终有∠BCQ=60°.点A是MN上方一定点,点D是PQ下方一定点,且AEBCDF,AE=4,DF=8,AD=24,当线段BC在平移过程中,AB+CD的最小值为( )
A.24 B.24 C.12 D.12
9.如图,在平面直角坐标系中,点A的坐标是,点C的坐标是,点是x轴上的动点,点B在x轴上移动时,始终保持是等边三角形(点P不在第二象限),连接,求得的最小值为( )
A. B.4 C. D.2
10.如图,MN是正方形ABCD的对称轴,沿折痕DF,DE折叠,使顶点A,C落在MN上的点G.给出4个结论:①∠BFE=30°;②△FGM∽△DEG;③;④.其中正确的是( )
A.①②③ B.②③④ C.①③④ D.①②④
二、填空题(本大题共8小题,每小题4分,共32分)
11.若,则 .
12.如图,平面内几条线段满足.AB、CD的交点为E,现测得,,,则CD的长度为 .
13.如图,中,,以为轴,轴经过点,建立平面直角坐标系,已知,,将沿着轴翻折,的对应点为,若抛物线 ,恰好过、、,则
14.在平面直角坐标系中,已知,,点是直线上的一点,连接、.当在一定范围内取值时,直线上总存在点,使得,则此时的取值范围为 .
15.如图,菱形绕A点顺时针旋转,B、C、D的对应点分别为、、,若和D重合,菱形面积为,则阴影的面积= .
16.如图,现有一矩形纸片,为矩形的对角线,,,点为上一点,沿线段将折叠为,交于点,连接,作点关于线段对称的点,点恰好落在对角线上,连接,.则的大小为 ;的长为 .
17.如图,三角形中,于,以为边作菱形,使点落在边上,点在上,交于点,若,,则的长为 .
18.如图,在平面直角坐标系中,的顶点A在直线上,顶点B在x轴上,垂直轴,且,顶点在直线上,;过点作直线的垂线,垂足为,交x轴于,过点作垂直x轴,交于点,连接,得到第一个;过点作直线的垂线,垂足为,交x轴于,过点作垂直x轴,交于点,连接,得到第二个;如此下去,……,则的面积是 .
三、解答题(本大题共6小题,共58分)
19.(8分)计算下列的三角函数值(写出计算过程,保留计算结果):
.
20.(8分)如图所示,,上有一点,,,
(1)用含的表达式表示出AC的长度
(2)用含的表达式表示出点D到AC的距离
21.(10分)如图.△ABC中.AB=BC=.AC=4.D为AC的中点.E、F分别为AD、CD上的动点.过E作PE⊥AD.且DE+2PE=2.连接PF.
(1)求sin∠C;
(2)连接AP.
①求证AP∥BC;
②请直接写出PF+CF的最大值.
22.(10分)如图,计划在山顶A的正下方沿直线CD方向开通穿山隧道EF.在点E处测得山顶A的仰角为45°,在距E点80m的C处测得山顶A的仰角为30°,从与F点相距10m的D处测得山顶A的仰角为45°,点C、E、F、D在同一直线上,求隧道EF的长度.
23.(10分)圣·索菲亚教堂坐落于中国黑龙江省,是一座始建于1907年拜占庭风格的东正教教堂,被列为第四批全国重点文物保护单位,其中央主体建筑集球、圆柱、棱柱于一体,极具对称之美,可以让游客从任何角度都能领略它的美,如图,小明为了估算索菲亚教堂的高度,在索菲亚教堂的正东方向找到一座建筑物,高为6m,在它们之间的地面上的点M(B,M,D三点共线)处测得建筑物顶A,教堂顶C的仰角分别是15°和60°,在楼顶A处测得教堂顶C的仰角为30°,那么小明计算索菲亚教堂的高度为多少? (保留根号,,,)
24.(12分)(2022·河北石家庄·校联考三模)小明在一段斜坡上进行跑步训练.在训练过程中,始终有一架无人机在小明正上方随他一起运动,无人机速度为,距水平地面的高度总为(在直线上运动)现就小明训练中部分路段作出如图函数图象:已知,斜坡的坡度:,斜坡的坡角为.
(1)点坐标为______,段关于的函数解析式为______;
(2)小明在斜坡上的跑步速度是______,并求段关于的函数解析式;
(3)若小明沿方向运动,求无人机与小明之间距离不超过10m的时长.(参考数据:,,)
答案
1.D
【分析】根据锐角三角函数值的计算,以及二次根式的运算,逐一进行判断即可.
解:A、,选项错误,不符合题意;
B、,选项错误,不符合题意;
C、,选项错误,不符合题意;
D、,选项正确,符合题意.
故选D.
2.A
【分析】由题可知,秋千摆到最低点时,点为弧的中心 ,由垂径定理知,.再根据锐角三角函数解三角形求得即可.
解:∵点为弧的中点,为圆心,
由垂径定理知,,,
∵,
∴,
∵,
在中,由三角函数可得,
∴,
故选:A.
3.C
【分析】由可知,OP与x轴的夹角为45°,又因为,则为等腰直角形,设OC=x,OB=2x,用勾股定理求其他线段进而求解.
解:∵P点坐标为(1,1),
则OP与x轴正方向的夹角为45°,
又∵,
则∠BAO=45°,为等腰直角形,
∴OA=OB,
设OC=x,则OB=2OC=2x,
则OB=OA=3x,
∴.
4.C
【分析】由勾股定理分别算出三边的长度,再利用勾股定理逆定理证明是直角三角形,再根据锐角三角函数进行求解,通过证明继而进行判断即可.
解:由题意得,,
,
是直角三角形,,故B正确,不符合题意;
,故A正确,不符合题意;
,
,
,
,
,
,
,故C错误,符合题意;
,故D正确,不符合题意;
故选:C.
5.A
【分析】先证明,,,,,可得,,再利用正切的定义求解即可.
解:∵矩形纸片对折,折痕为,,,
∴,,,,
由折叠可得:,
∴,
∴,
∴.
故选A
6.B
【分析】在中,根据锐角三角函数的定义得出,代入,两边平方得出,由“赵爽弦图”,结合图形可知等于小正方形的边长,那么.再根据,即可求解.
解:如图.
在中,∵,
∴.
∵,
∴,
∴,
即.
设,则,
∴,
∴.
故选:B.
7.A
【分析】连接由题意可得,进而说明为等腰直角三角形,再说明垂直平分、垂直平分,进而说明,然后再运用解直角三角形求得,然后再求得三角形的面积,最后求风车面积即可.
解:如图:连接
由题意可得:
,
为等腰直角三角形
又 :
,
,即
又
垂直平分
同理:垂直平分
是等腰三角形顶角的角平分线
即
由题意可得
又,
,
在中,,
,
设,即
,
,
设(),,
,即,
,
又,
,
,
.
故选A.
8.C
【分析】如图所示,过点F作交BC于H,连接EH,可证明四边形CDFH是平行四边形,得到CH=DF=8,CD=FH,则BH=4,从而可证四边形ABHE是平行四边形,得到AB=HE,即可推出当E、F、H三点共线时,EH+HF有最小值EF即AB+CD有最小值EF,延长AE交PQ于G,过点E作ET⊥PQ于T,过点A作AL⊥PQ于L,过点D作DK⊥PQ于K,证明四边形BEGC是平行四边形,∠EGT=∠BCQ=60°,得到EG=BC=12,然后通过勾股定理和解直角三角形求出ET和TF的长即可得到答案.
解:如图所示,过点F作交BC于H,连接EH,
∵,
∴四边形CDFH是平行四边形,
∴CH=DF=8,CD=FH,
∴BH=4,
∴BH=AE=4,
又∵,
∴四边形ABHE是平行四边形,
∴AB=HE,
∵,
∴当E、F、H三点共线时,EH+HF有最小值EF即AB+CD有最小值EF,
延长AE交PQ于G,过点E作ET⊥PQ于T,过点A作AL⊥PQ于L,过点D作DK⊥PQ于K,
∵,
∴四边形BEGC是平行四边形,∠EGT=∠BCQ=60°,
∴EG=BC=12,
∴,
同理可求得,,
∴,
∵AL⊥PQ,DK⊥PQ,
∴,
∴△ALO∽△DKO,
∴,
∴,
∴,
∴,
∴,
故选C.
9.C
【分析】如图1所示,以OA为边,向右作等边△AOD,连接PD,过点D作DE⊥OA于E,先求出点D的坐标,然后证明△BAO≌△PAD得到∠PDA=∠BOA=90°,则点P在经过点D且与AD垂直的直线上运动,当点P运动到y轴时,如图2所示,证明此时点P的坐标为(0,-2)从而求出直线PD的解析式;如图3所示,作点A关于直线PD的对称点G,连接PG,过点P作PF⊥y轴于F,设直线PD与x轴的交点为H,先求出点H的坐标,然后证明∠HCO=30°,从而得到,则当G、P、F三点共线时,有最小值,即有最小值,再根据轴对称的性质求出点G在x轴上,则OG即为所求.
解:如图1所示,以OA为边,向右作等边△AOD,连接PD,过点D作DE⊥OA于E,
∵点A的坐标为(0,2),
∴OA=OD=2,
∴OE=AE=1,
∴,
∴点D的坐标为;
∵△ABP是等边三角形,△AOD是等边三角形,
∴AB=AP,∠BAP=60°,AO=AD,∠OAD=60°,
∴∠BAP+∠PAO=∠DAO+∠PAO,即∠BAO=∠PAD,
∴△BAO≌△PAD(SAS),
∴∠PDA=∠BOA=90°,
∴点P在经过点D且与AD垂直的直线上运动,
当点P运动到y轴时,如图2所示,此时点P与点C重合,
∵△ABP是等边三角形,BO⊥AP,
∴AO=PO=2,
∴此时点P的坐标为(0,-2),
设直线PD的解析式为,
∴,
∴,
∴直线PD的解析式为;
如图3所示,作点A关于直线PD的对称点G,连接PG,过点P作PF⊥y轴于F,连接CG,设直线PD与x轴的交点为H,
∴点H的坐标为,
∴,
∴∠OCH=30°,
∴,
由轴对称的性质可知AP=GP,
∴,
∴当G、P、F三点共线时,有最小值,即有最小值,
∵A、G两点关于直线PD对称,且∠ADC=90°,
∴AD=GD,即点D为AG的中点,
∵点A的坐标为(0,2),点D的坐标为,
∴AG=2AD=2OA=4,
∵AC=4,∠CAG=60°,
∴△ACG是等边三角形,
∵OC=OA,
∴OG⊥AC,即点G在x轴上,
∴由勾股定理得,
∴当点P运动到H点时,有最小值,即有最小值,最小值即为OG的长,
∴的最小值为,
故选:C.
10.D
【分析】设,根据折叠的性质得,,根据轴对称的性质得出,即可判断①,从而得出,,继而判断②,设,则,解,即可判断③,分别求得即可判断④.
解:设,根据折叠的性质得,,
四边形是正方形,则,
,
设正方形的边长为,则,
MN是正方形ABCD的对称轴,
,
,
,
,
,
,故①正确,
,
,,
,,
△FGM∽△DEG;故②正确,
设,则,
在中,,
,
解得,
即,
,
故③不正确;
,
,
,
,
,
,
故④正确
故①②④正确,
故选D.
二、填空题
11.
【分析】根据锐角三角函数的增减性判断出与的大小、与 的大小,然后化简计算即可.
解:∵,
∴.
∴
,
故答案为:.
12.
【分析】延长交于,过作交于,根据“字形”可知,得到相似比,设,在中,根据勾股定理得,结合条件得出,再利用相似比即可求出的长度.
解:延长交于,过作交于,如图所示:
,
,
,
,
,
,
,
,
,,
,
设,则,
在中,根据勾股定理得,
,解得,
,解得,
故答案为:.
13.
【分析】根据题意得出,进而根据正切的定义,得出的坐标,进而求得点的坐标,根据轴对称的性质求得的坐标,待定系数法求得解析式,进而化为顶点式,即可求解.
解:∵中,,,
∴,
∴,
∵,
∴,设,则,
则,
∵,
∴,
即,,
∵,
∴,即,
∵将沿着轴翻折,的对应点为,
∴,
设抛物线解析式为,将点代入得,
解得:
∴抛物线解析式为
故答案为:.
14.且
【分析】先确定点,点的位置,并连接,过点作轴于,交轴于,作关于的对称点,连接,过点作交轴于,过点作交轴于,解出所在直线的解析式,再证明,由此解出直线,直线的解析式,由此即可求解.
解:根据题意,在平面直角坐标系中标出点,点,连接,作图如下,过点作轴于,交轴于,作关于的对称点,连接,过点作交轴于,过点作交轴于,则,直线和直线是符合条件的直线,理由如下,
设过点,点的直线方程为,
∴,解得,,
∴所在直线的解析式为,
∵,
∴直线,直线是符合条件的直线,
∵,,轴,
∴,
∴,
在中,,且,
∴,则,
∵,
∴,且,
∴,
∴,把代入得,,
∵点与点关于对称,
∴,,
∵,
∴,,
∴是等边三角形,
∴,则,
∴,把代入得,
∵点不能与点重合,
∴,
∴的取值范围为且.
15.
【分析】如图,过作交的延长线于,过作于,由旋转的性质可得:,可得,由菱形面积求解,证明,,可得,,,可得,从而可得答案.
解:如图,过作交的延长线于,过作于,
由旋转的性质可得:,
∴,
∵菱形面积为,
∴,
解得:,
由菱形的性质可得:,,
∴,
∴,
∴,
∴,
∴;
故答案为:.
16. 75
【分析】证明,可得;再证明,,求出,可得结论.
解:由折叠的性质可知,,
,关于对称,
,
,
,
,
,
,
.
,,,
,
,,
,,
,
,,
,.
故答案为:75;.
17.6
【分析】菱形的性质得到,推出,外角的性质,得到,进而得到,过点作于点,推出,利用锐角三角函数和勾股定理求出的长即可.
解:∵四边形为菱形,
∴,
∴,
∵,
∴,
过点作于点,设交于点,则,
∵,且,
∴,
∵,
∴,
∵,
∴,
在中,,
设,则:,
∴,
∴;
故答案为:.
18.
【分析】解直角三角形得出,,求出,证明,,得出,,总结得出,从而得出.
解:∵,
∴,
∵轴,
∴点A的横坐标为,
∵,
∴点A的纵坐标为,
∴,
∴,
∵,
∴设,则,
∴,
∴,
∴,
,
∵,
∴,
∴平分,
∵,,
∴,
∵,,
∴,
∴,
∴,
∴
,
∵,
∴,
∴,
∵,,,
∴,
∴,
∴,
∴,,
∵轴,轴,
∴,,
∵轴,轴,轴,
∴,
∴,,
∵,
∴,,
∴,
∵,
∴,
同理,
∴,
,
∴,
∴.
故答案为:.
三、解答题
19.
解:
20.
(1)解:在中,,,,
∴,
在中,,,
∴;
(2)解:在中,,,
∴,
则,
设点D到AC的距离为h,
由得
.
21.
(1)解:连接BD,如下图,
∵,
∴是等腰三角形.
∵D为AC的中点,
∴.
∵,
∴,
∴,
∴;
(2)解:①∵,
设,
则,
∴.
∵由(1)得,,
∴,
∴.
∵,
∴,
∴,
∴,
∴;
②由①,,PE⊥AD,
∴.
∵E、F分别为AD、CD上的动点,使为中点,
则,,
∴.
∵ ,且,x不能小于0,
∴,
解得,
∴,
∴当时,有最大值,最大值是.
22.
解:过点A作AG⊥CD于点G,如图所示:
由题意得:,
∴△EAD是等腰直角三角形,
∴AG=EG=DG,
设AG=EG=DG=x,
∴,
∴,
解得:,
∴,
∴;
答:隧道EF的长度米.
23.
解:如图,过作于,则四边形是矩形,
∴,,
∵,
∴,
设,则,,
∴,,
∵,
∴,
∴,
解得:,
∴,
∴索菲亚教堂的高度为米.
24.
(1)解:如图,过A点作于点,
,
,
,斜坡的坡度::,
,,
点A坐标为,
设段关于的函数解析式为,
代入,,
解得:,
段关于的函数解析式
,
故答案为:;.
(2)解:在中,,,
,
,
,,
在训练过程中,始终有一架无人机在小明正上方随他一起运动.无人机速度为,
小明在斜坡上跑步的时间为:,
小明在斜坡上的跑步速度是:,
,,
,
,
设段关于的函数解析式为:代入,,
得:,
解得:,
段关于的函数解析式为;
故答案为:.
(3)解:在段上无人机与小明之间的距离为时,
则有:,
解得:,
无人机飞行的时间为;
在段上,无人机与小明之间距离为时,则有:,
解得:,
无人机飞行的时间为,
无人机与小明之间距离不超过的时长为:.
