北师大版数学九年级下册 专项练习三 解直角三角形(含答案)
文档属性
| 名称 | 北师大版数学九年级下册 专项练习三 解直角三角形(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 506.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-05 20:56:04 | ||
图片预览


文档简介
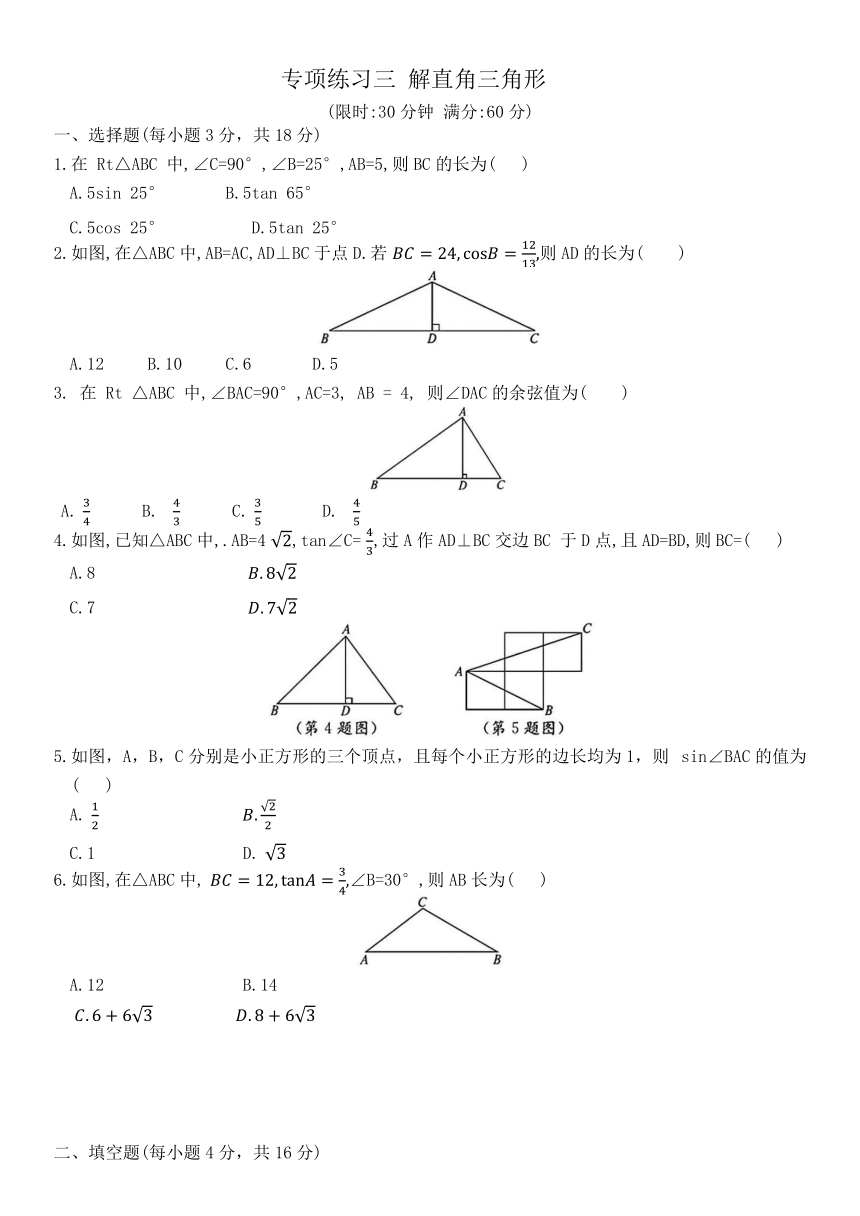
专项练习三 解直角三角形
(限时:30分钟 满分:60分)
一、选择题(每小题3分,共18分)
1.在 Rt△ABC 中,∠C=90°,∠B=25°,AB=5,则BC的长为( )
A.5sin 25° B.5tan 65°
C.5cos 25° D.5tan 25°
2.如图,在△ABC中,AB=AC,AD⊥BC于点D.若 则AD的长为( )
A.12 B.10 C.6 D.5
3. 在 Rt △ABC 中,∠BAC=90°,AC=3, AB = 4, 则∠DAC的余弦值为( )
A. B. C. D.
4.如图,已知△ABC中,.AB=4 ,tan∠C= ,过A作AD⊥BC交边BC 于D点,且AD=BD,则BC=( )
A.8
C.7
5.如图,A,B,C分别是小正方形的三个顶点,且每个小正方形的边长均为1,则 sin∠BAC的值为( )
A.
C.1 D.
6.如图,在△ABC中, ∠B=30°,则AB长为( )
A.12 B.14
二、填空题(每小题4分,共16分)
7. 如图,在△ABC 中,∠B =30°,AC=2, 则AB边的长为 .
C
8.如图,在△ABC中, AB=3,则AC的长为 .
9.如图,在 Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为 D. AF 平分∠CAB,交 BC 于点 F,交CD于点 E.若 则DE的长为 .
10.如图,在 Rt△BAD 中,延长斜边 BD 到点C,使 连接AC,若 则tan∠CAD的值为 .
三、解答题(共26分)
11.(8 分)在 Rt△ABC中,∠C=90°,AC= 解这个直角三角形.
12.(9 分)如图所示,△ABC 中,∠B=45°,∠C=30°,AB=2 求 BC的长..
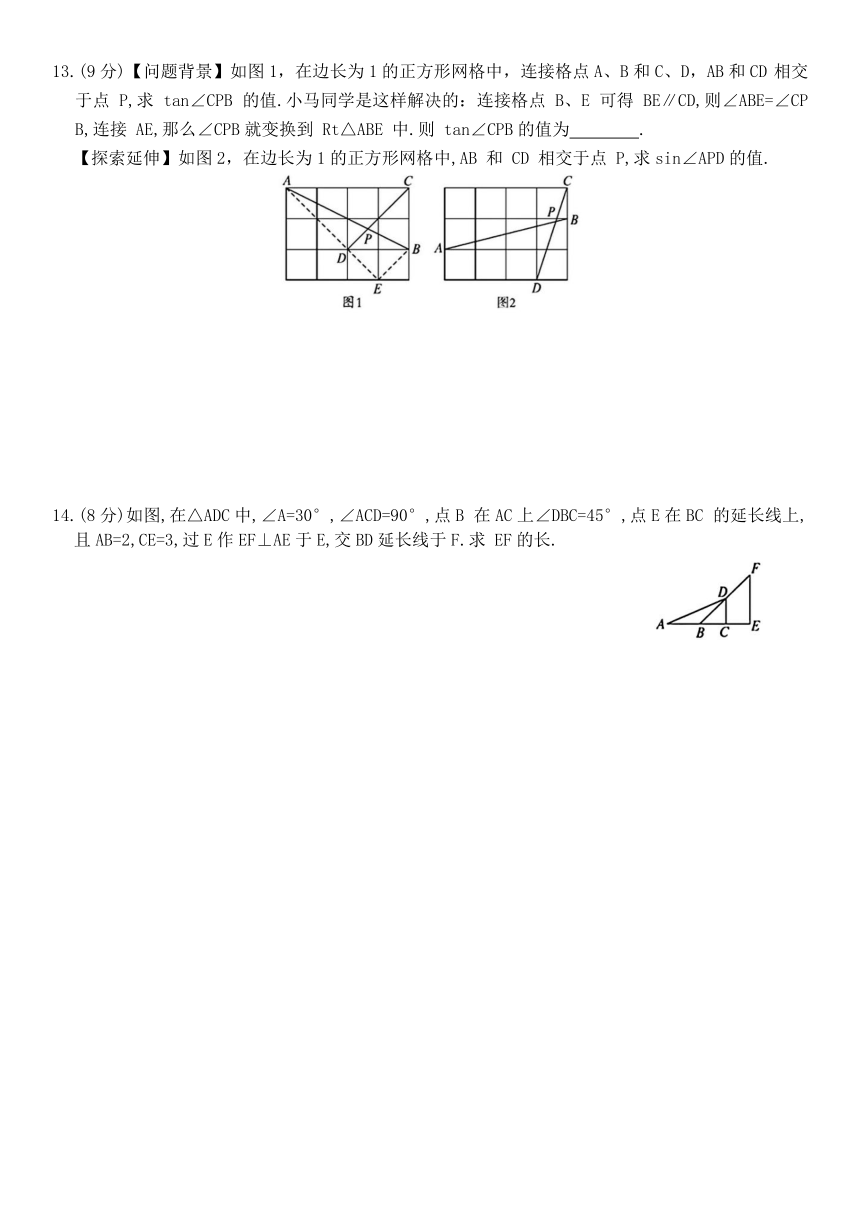
13.(9分)【问题背景】如图1,在边长为1的正方形网格中,连接格点A、B和C、D,AB和CD 相交于点 P,求 tan∠CPB 的值.小马同学是这样解决的:连接格点 B、E 可得 BE∥CD,则∠ABE=∠CPB,连接 AE,那么∠CPB就变换到 Rt△ABE 中.则 tan∠CPB的值为 .
【探索延伸】如图2,在边长为1的正方形网格中,AB 和 CD 相交于点 P,求sin∠APD的值.
14.(8分)如图,在△ADC中,∠A=30°,∠ACD=90°,点B 在AC上∠DBC=45°,点E在BC 的延长线上,且AB=2,CE=3,过E作EF⊥AE于E,交BD延长线于F.求 EF的长.
15.(10分)两栋居民楼之间的距离楼AC和BD 均为10层,每层楼高为3m .上午某时刻,太阳光线GB 与水平面的夹角为 ,此刻楼 BD的影子会遮挡到楼AC的第几层 (参考数据:
专项练习三 解直角三角形
1. C 2. D 3. D 4. C 5. B 6. D
8.
11.解:∵在Rt△ABC中,
即
12.解:过点A作AD⊥BC于点D,如图所示.
在Rt△ABD中,
在Rt△ACD中,
13.解:(1)如图1,
故答案为3.
(2)如图2,连接CE,DE,作. 于M.
∴四边形ABCE是平行四边形,
∵△ECD的面积
14.解:设BC=x.
∵∠DBC=45°,EF⊥AE,∴EF=BE,BC=DC,
∴AC=2+x,
15.解:如图,设太阳光线GB交AC 于点F,过F作FH⊥BD于 H.
由题意知,AC=BD=3×10=30m,FH=CD=30 m,∠BFH=∠α=30°,
在Rt△BFH中,
∴FC=HD=BD-BH≈30-17=13,
∴在四层的上面,即第五层.
答:此刻楼BD的影子会遮挡到楼AC的第五层.
(限时:30分钟 满分:60分)
一、选择题(每小题3分,共18分)
1.在 Rt△ABC 中,∠C=90°,∠B=25°,AB=5,则BC的长为( )
A.5sin 25° B.5tan 65°
C.5cos 25° D.5tan 25°
2.如图,在△ABC中,AB=AC,AD⊥BC于点D.若 则AD的长为( )
A.12 B.10 C.6 D.5
3. 在 Rt △ABC 中,∠BAC=90°,AC=3, AB = 4, 则∠DAC的余弦值为( )
A. B. C. D.
4.如图,已知△ABC中,.AB=4 ,tan∠C= ,过A作AD⊥BC交边BC 于D点,且AD=BD,则BC=( )
A.8
C.7
5.如图,A,B,C分别是小正方形的三个顶点,且每个小正方形的边长均为1,则 sin∠BAC的值为( )
A.
C.1 D.
6.如图,在△ABC中, ∠B=30°,则AB长为( )
A.12 B.14
二、填空题(每小题4分,共16分)
7. 如图,在△ABC 中,∠B =30°,AC=2, 则AB边的长为 .
C
8.如图,在△ABC中, AB=3,则AC的长为 .
9.如图,在 Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为 D. AF 平分∠CAB,交 BC 于点 F,交CD于点 E.若 则DE的长为 .
10.如图,在 Rt△BAD 中,延长斜边 BD 到点C,使 连接AC,若 则tan∠CAD的值为 .
三、解答题(共26分)
11.(8 分)在 Rt△ABC中,∠C=90°,AC= 解这个直角三角形.
12.(9 分)如图所示,△ABC 中,∠B=45°,∠C=30°,AB=2 求 BC的长..
13.(9分)【问题背景】如图1,在边长为1的正方形网格中,连接格点A、B和C、D,AB和CD 相交于点 P,求 tan∠CPB 的值.小马同学是这样解决的:连接格点 B、E 可得 BE∥CD,则∠ABE=∠CPB,连接 AE,那么∠CPB就变换到 Rt△ABE 中.则 tan∠CPB的值为 .
【探索延伸】如图2,在边长为1的正方形网格中,AB 和 CD 相交于点 P,求sin∠APD的值.
14.(8分)如图,在△ADC中,∠A=30°,∠ACD=90°,点B 在AC上∠DBC=45°,点E在BC 的延长线上,且AB=2,CE=3,过E作EF⊥AE于E,交BD延长线于F.求 EF的长.
15.(10分)两栋居民楼之间的距离楼AC和BD 均为10层,每层楼高为3m .上午某时刻,太阳光线GB 与水平面的夹角为 ,此刻楼 BD的影子会遮挡到楼AC的第几层 (参考数据:
专项练习三 解直角三角形
1. C 2. D 3. D 4. C 5. B 6. D
8.
11.解:∵在Rt△ABC中,
即
12.解:过点A作AD⊥BC于点D,如图所示.
在Rt△ABD中,
在Rt△ACD中,
13.解:(1)如图1,
故答案为3.
(2)如图2,连接CE,DE,作. 于M.
∴四边形ABCE是平行四边形,
∵△ECD的面积
14.解:设BC=x.
∵∠DBC=45°,EF⊥AE,∴EF=BE,BC=DC,
∴AC=2+x,
15.解:如图,设太阳光线GB交AC 于点F,过F作FH⊥BD于 H.
由题意知,AC=BD=3×10=30m,FH=CD=30 m,∠BFH=∠α=30°,
在Rt△BFH中,
∴FC=HD=BD-BH≈30-17=13,
∴在四层的上面,即第五层.
答:此刻楼BD的影子会遮挡到楼AC的第五层.
