1.2 空间向量基本定理 课件(共28张PPT)
文档属性
| 名称 | 1.2 空间向量基本定理 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-05 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
1.2 空间向量基本定理的应用(二)
1.空间向量基本定理
如果三个向量 不共面,那么对任意一个空间向量 ,存在唯一的有序实数组( x,y,z),使得
都叫做基向量
叫做空间的一个基底,空间任意三个不共面向量都可以构成空间的一个基底.
所有空间向量组成的集合为
一、回顾旧知
特别地,如果空间的一个基底中的三个基向量两两互相垂直,且长度都为1,那么这个基底叫做单位正交基底,常用 表示.
2.单位正交基底
由空间向量基本定理可知,对空间中的任意向量 ,均可以分解为三个向量 ,使 .
把一个空间向量分解为三个两两互相垂直的向量,叫做把空间向量进行正交分解.
3.正交分解
一、回顾旧知
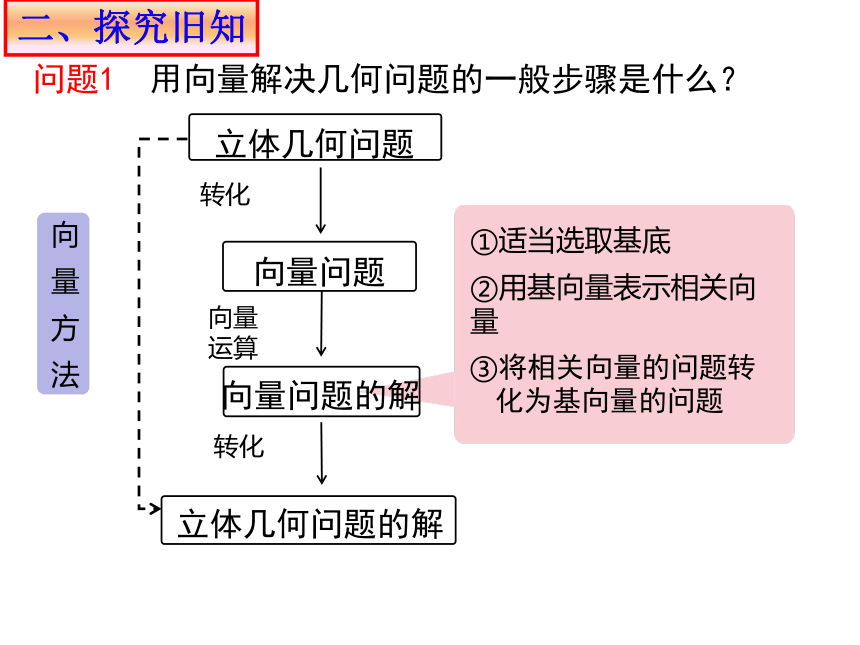
立体几何问题
①适当选取基底
向量
运算
②用基向量表示相关向量
③将相关向量的问题转化为基向量的问题
向量问题
向量问题的解
立体几何问题的解
转化
向量方法
转化
问题1 用向量解决几何问题的一般步骤是什么?
二、探究旧知
小试牛刀√√×D例1:如图所示,正三棱柱ABC-A1B1C1
的所有棱长都为2,D为CC1的中点.
求证:AB1⊥平面A1BD.
应用空间向量基本定理证明平行、垂直
用向量法证明垂直关系的步骤
(1)把几何问题转化为向量问题.
(2)选择空间的某个基底表示未知向量.
(3)结合数量积公式和运算律证明数量积为0.
(4)将向量问题回归到几何问题.
例2:在直三棱柱ABC-A′B′C′中,AC=BC=AA′,∠ACB=90°,D,E分别为AB,BB′的中点.
(1)求证:CE⊥A′D;
(2)求异面直线CE与AC′所成角的余弦值.
应用空间向量基本定理求夹角、距离
例2:在直三棱柱ABC-A′B′C′中,AC=BC=AA′,∠ACB=90°,D,E分别为AB,BB′的中点.
(1)求证:CE⊥A′D;
(2)求异面直线CE与AC′所成角的余弦值.
应用空间向量基本定理求夹角、距离
A′
B′
C′
D′
A
B
C
D
G
E
F
O
例3.
单位正交基底:如果空间的一个基底的三个基向量互相垂直,且长都为1,则这个基底叫做单位正交基底.
例4.
例6.
应用空间向量基本定理证明平行、垂直
应用空间向量基本定理求夹角、距离
利用数量积求夹角或其余弦值的步骤
1.知识清单:(1)利用空间向量基本定理证明平行、垂直.
(2)利用空间向量基本定理求夹角、距离.
2.方法归纳:数形结合、转化的思想.
三、课堂小结
1.2 空间向量基本定理的应用(二)
1.空间向量基本定理
如果三个向量 不共面,那么对任意一个空间向量 ,存在唯一的有序实数组( x,y,z),使得
都叫做基向量
叫做空间的一个基底,空间任意三个不共面向量都可以构成空间的一个基底.
所有空间向量组成的集合为
一、回顾旧知
特别地,如果空间的一个基底中的三个基向量两两互相垂直,且长度都为1,那么这个基底叫做单位正交基底,常用 表示.
2.单位正交基底
由空间向量基本定理可知,对空间中的任意向量 ,均可以分解为三个向量 ,使 .
把一个空间向量分解为三个两两互相垂直的向量,叫做把空间向量进行正交分解.
3.正交分解
一、回顾旧知
立体几何问题
①适当选取基底
向量
运算
②用基向量表示相关向量
③将相关向量的问题转化为基向量的问题
向量问题
向量问题的解
立体几何问题的解
转化
向量方法
转化
问题1 用向量解决几何问题的一般步骤是什么?
二、探究旧知
小试牛刀√√×D例1:如图所示,正三棱柱ABC-A1B1C1
的所有棱长都为2,D为CC1的中点.
求证:AB1⊥平面A1BD.
应用空间向量基本定理证明平行、垂直
用向量法证明垂直关系的步骤
(1)把几何问题转化为向量问题.
(2)选择空间的某个基底表示未知向量.
(3)结合数量积公式和运算律证明数量积为0.
(4)将向量问题回归到几何问题.
例2:在直三棱柱ABC-A′B′C′中,AC=BC=AA′,∠ACB=90°,D,E分别为AB,BB′的中点.
(1)求证:CE⊥A′D;
(2)求异面直线CE与AC′所成角的余弦值.
应用空间向量基本定理求夹角、距离
例2:在直三棱柱ABC-A′B′C′中,AC=BC=AA′,∠ACB=90°,D,E分别为AB,BB′的中点.
(1)求证:CE⊥A′D;
(2)求异面直线CE与AC′所成角的余弦值.
应用空间向量基本定理求夹角、距离
A′
B′
C′
D′
A
B
C
D
G
E
F
O
例3.
单位正交基底:如果空间的一个基底的三个基向量互相垂直,且长都为1,则这个基底叫做单位正交基底.
例4.
例6.
应用空间向量基本定理证明平行、垂直
应用空间向量基本定理求夹角、距离
利用数量积求夹角或其余弦值的步骤
1.知识清单:(1)利用空间向量基本定理证明平行、垂直.
(2)利用空间向量基本定理求夹角、距离.
2.方法归纳:数形结合、转化的思想.
三、课堂小结
