2024年甘肃省兰州市安宁区西北师大二附中中考数学四模试卷(含答案)
文档属性
| 名称 | 2024年甘肃省兰州市安宁区西北师大二附中中考数学四模试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 320.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-06 10:50:53 | ||
图片预览




文档简介
2024年甘肃省兰州市安宁区西北师大二附中中考数学四模试卷
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的相反数是( )
A. B. C. D.
2.把多项式分解因式得( )
A. B. C. D.
3.用配方法解方程时,配方后正确的是( )
A. B. C. D.
4.如图,直线 ,,,则的度数是 ( )
A. B. C. D.
5.如图,在平面直角坐标系中,矩形的顶点在坐标原点,边在轴上,在轴上,如果矩形与矩形关于点位似,且矩形的面积等于矩形面积的,那么点的坐标是( )
A. B.
C. 或 D. 或
6.大自然中有许多小动物都是“小数学家”,如图,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图,一个巢房的横截面为正六边形,若对角线的长约为,则正六边形的边长为( )
A. B. C. D.
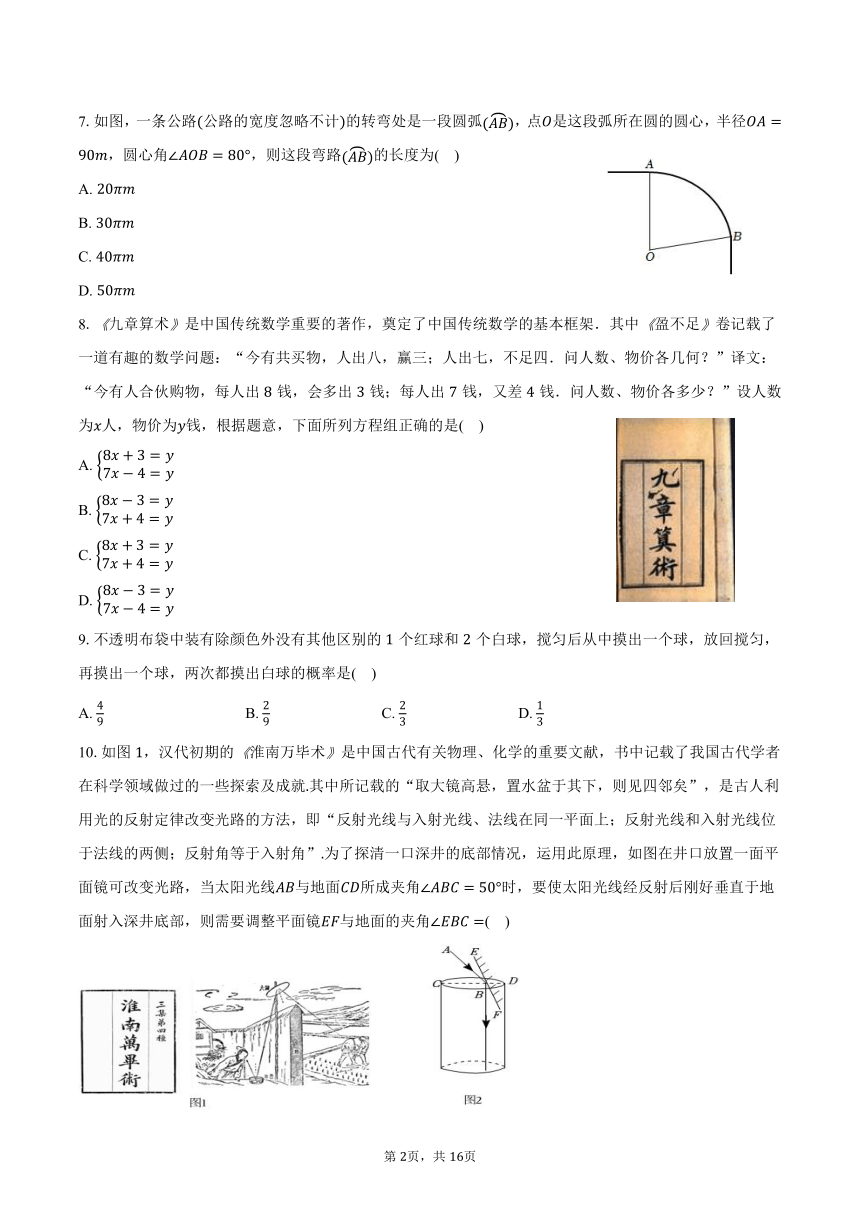
7.如图,一条公路公路的宽度忽略不计的转弯处是一段圆弧,点是这段弧所在圆的圆心,半径,圆心角,则这段弯路的长度为( )
A.
B.
C.
D.
8.九章算术是中国传统数学重要的著作,奠定了中国传统数学的基本框架.其中盈不足卷记载了一道有趣的数学问题:“今有共买物,人出八,赢三;人出七,不足四.问人数、物价各几何?”译文:“今有人合伙购物,每人出钱,会多出钱;每人出钱,又差钱.问人数、物价各多少?”设人数为人,物价为钱,根据题意,下面所列方程组正确的是( )
A.
B.
C.
D.
9.不透明布袋中装有除颜色外没有其他区别的个红球和个白球,搅匀后从中摸出一个球,放回搅匀,再摸出一个球,两次都摸出白球的概率是( )
A. B. C. D.
10.如图,汉代初期的淮南万毕术是中国古代有关物理、化学的重要文献,书中记载了我国古代学者在科学领域做过的一些探索及成就其中所记载的“取大镜高悬,置水盆于其下,则见四邻矣”,是古人利用光的反射定律改变光路的方法,即“反射光线与入射光线、法线在同一平面上;反射光线和入射光线位于法线的两侧;反射角等于入射角”为了探清一口深井的底部情况,运用此原理,如图在井口放置一面平面镜可改变光路,当太阳光线与地面所成夹角时,要使太阳光线经反射后刚好垂直于地面射入深井底部,则需要调整平面镜与地面的夹角( )
A. B. C. D.
11.如图,在中,,,,以点为圆心,长为半径画弧,与交于点,再分别以、为圆心,大于的长为半径画弧,两弧交于点、,作直线,分别交、于点、,则的长度为( )
A.
B.
C.
D.
12.如图,等边、等边的边长分别为和开始时点与点重合,在上,在上,沿向右平移,当点到达点时停止.在此过程中,设、重合部分的面积为,移动的距离为,则与的函数图象大致为( )
A. B.
C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.若二次根式有意义,则的取值范围是______.
14.若一元二次方程有两个相等的实数根,则的值为______.
15.如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度单位:与飞行时间单位:之间具有函数关系:,则当小球飞行高度达到最高时,飞行时间______
16.如图,点是矩形中边上一点,沿折叠得到对应的,且点的对应点落在上.若,,则______.
三、解答题:本题共11小题,共66分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:.
18.本小题分
解不等式组:.
19.本小题分
解分式方程:.
20.本小题分
古希腊数学家欧几里得约公元前公元前,被称为“几何学之父”,在其所著的几何原本中第卷给出其中一个命题:如果从圆外的一点向圆引两条直线,一条与圆相切,一条穿过圆,那么被圆截得的线段与该点到凸圆之间的线段为边构成的矩形的面积等于以该点向圆引的切线为边所构成的正方形的面积命题解读:直线为的切线,直线为圆的割线,以为边构造正方形,以,为边构造矩形,可得正方形的面积等于矩形的面积,由此可得.
根据以上问题,完成尺规作图并计算.
尺规作图步骤如下:以点为圆心,小于的长为半径作弧,交射线于,两点;分别以,为圆心,大于的长为半径作弧,两弧交于点;作射线,射线与射线交于点;可得直线为的切线请按描述完成作图;
依据所作图形,若以为边的正方形的面积为,::,则以,为边的矩形的周长为______.
21.本小题分
某学习小组在物理实验结束后,利用实验装置探究几何测量问题.
课题 探究物理实验装置中的几何测量问题
成员 组长:组员:,,
实验工具 测角仪,皮尺,摄像机等
方案一 方案二
测量方案示意图
已知
已知
说明 点为摄像机的位置,小车从同一斜面上相同高度处由静止开始沿斜面下滑,点为小车从斜面到达水平面的位置,点为木块的位置.
测量数据 米,, 米,,.
请选择其中一种方案计算出摄像机机位到小车行驶轴线的竖直距离结果精确到米,参考数据,,
22.本小题分
如图,是的直径,是的弦,平分交于点,过点作的切线,交的延长线于点,交的延长线于点.
求证;
若,,求的长.
23.本小题分
如图,一次函数的图象与反比例函数的图象交于点,.
求反比例函数与一次函数的解析式;
请结合图象直接写出不等式的解集;
若点为轴上一点,的面积为,求点的坐标.
24.本小题分
小红看到一处喷水景观,喷出的水柱呈抛物线形状,她对此展开研究:测得喷水头距地面,水柱在距喷水头水平距离处达到最高,最高点距地面;建立如图所示的平面直角坐标系,并设抛物线的表达式为,其中是水柱距喷水头的水平距离,是水柱距地面的高度.
求抛物线的表达式.
爸爸站在水柱正下方,且距喷水头水平距离身高的小红在水柱下方走动,当她的头顶恰好接触到水柱时,求她与爸爸的水平距离.
25.本小题分
如图,在 中,点,分别在,上,与相交于点,,.
求证:四边形是矩形;
若,,,求四边形的面积.
26.本小题分
问题情境:
在综合实践课上,同学们以“正方形的旋转”为主题开展活动如图,四边形和四边形都是正方形,边长分别是和,将顶点与顶点重合,正方形绕点逆时针方向旋转,连接,.
初步探究:
试猜想线段与的关系,并加以证明;
问题解决:
如图,在正方形的旋转过程中,当点恰好落在边上时,连接,求线段的长;
在图中,若与交于点,请直接写出线段的长.
27.本小题分
【概念学习】
对于平面直角坐标系中的图形和图形,给出如下定义:,分别为图形和图形上任意一点,将,两点间距离的最小值称为图形和图形之间的“关联距离”,记作例如,如图,点与轴之间的“关联距离”轴.
【理解概念】
如图,已知点在边长为的正方形内,则,正方形 ______.
【深入探索】
如图,在等边中,点的坐标是,点,在轴上,点是轴上一点,若,求点的坐标.
【拓展延伸】
已知,,当时,对于每一个,若线段和一次函数是常数,的图象之间的“关联距离”,直线,则的取值范围是______.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:
.
18.解:解不等式得:,
解不等式得:,
则不等式组的解集为.
19.解:去分母得:,
移项得:,
合并同类项得:,
解得:,
检验:把代入得:,
分式方程的解为.
【答案】如图所示;
令,则,
,
以为边的正方形的面积为,
,
,
,
舍去负值,
,,
以,为边的矩形的周长.
21.解:选择方案一:设米,则米,
在中,,
在中,,
,
解得:,
米,
答:摄像机机位到小车行驶轴线的竖直距离约为米.
22.解:证明:连接,
切于,
,
平分,
,
,
,
,
,
;
解:,
∽,
::,
,
,
,,
,
::,
.
23.解:一次函数的图象与反比例函数的图象交于点,.
,
,,
反比例函数解析式为,
点,在一次函数的图象上,
,解得,
一次函数解析式为.
根据函数图象及列函数图象的交点坐标可知,不等式的解集为:或.
在一次函数中,当时,,
,
设点坐标为,则丨丨,
,
解得:或,
或.
24.解:由题意知,抛物线顶点为,
设抛物线的表达式为,将代入得:
,
解得:,
,
答:抛物线的表达式为;
当时,,
解得:或,
她与爸爸的水平距离为或,
答:当她的头顶恰好接触到水柱时,与爸爸的水平距离是或.
25.证明:在 中,,,
,
,
即,
四边形是平行四边形,
,
四边形是矩形;
解:四边形是矩形,
,;
,
勾股定理得;
在中,,
,
由勾股定理得,
,
,
而,
.
26.解:,,
证明:如图,
四边形和四边形是正方形,
,,,
,
,
≌,
,,
延长,相交于点,的延长线交于,
,
,
,
,
,
即,;
在中,,,
根据勾股定理得,,
如图,过点作,交的延长线于,
四边形是正方形,
,,
,
四边形是正方形,
,,
,
,
≌,
,,
,,
,
;
如图,由知,,
四边形是正方形,
,
,
,
由知,,,
,
.
27. 且
【解析】解:与边长为的正方形的边上的点的最小距离为,
根据“关联距离”的定义得:,正方形,
故答案为:;
当在上方时,如图:
,
,
的坐标是,
的坐标是;
当在线段上时,过作于,如图:
,
,
是等边三角形,,
,
,
的坐标是,
,
;
当在下方时,如图:
,
,
;
综上所述,的坐标为或或;
如图:
当时,,
直线过定点,
当时,,,
当时,,,
把代入得:,
解得,
把代入得:,
解得,
线段和一次函数是常数,的图象之间的“关联距离”,直线,
直线与平行四边形无公共点,
由图可知,此时且.
第1页,共1页
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的相反数是( )
A. B. C. D.
2.把多项式分解因式得( )
A. B. C. D.
3.用配方法解方程时,配方后正确的是( )
A. B. C. D.
4.如图,直线 ,,,则的度数是 ( )
A. B. C. D.
5.如图,在平面直角坐标系中,矩形的顶点在坐标原点,边在轴上,在轴上,如果矩形与矩形关于点位似,且矩形的面积等于矩形面积的,那么点的坐标是( )
A. B.
C. 或 D. 或
6.大自然中有许多小动物都是“小数学家”,如图,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图,一个巢房的横截面为正六边形,若对角线的长约为,则正六边形的边长为( )
A. B. C. D.
7.如图,一条公路公路的宽度忽略不计的转弯处是一段圆弧,点是这段弧所在圆的圆心,半径,圆心角,则这段弯路的长度为( )
A.
B.
C.
D.
8.九章算术是中国传统数学重要的著作,奠定了中国传统数学的基本框架.其中盈不足卷记载了一道有趣的数学问题:“今有共买物,人出八,赢三;人出七,不足四.问人数、物价各几何?”译文:“今有人合伙购物,每人出钱,会多出钱;每人出钱,又差钱.问人数、物价各多少?”设人数为人,物价为钱,根据题意,下面所列方程组正确的是( )
A.
B.
C.
D.
9.不透明布袋中装有除颜色外没有其他区别的个红球和个白球,搅匀后从中摸出一个球,放回搅匀,再摸出一个球,两次都摸出白球的概率是( )
A. B. C. D.
10.如图,汉代初期的淮南万毕术是中国古代有关物理、化学的重要文献,书中记载了我国古代学者在科学领域做过的一些探索及成就其中所记载的“取大镜高悬,置水盆于其下,则见四邻矣”,是古人利用光的反射定律改变光路的方法,即“反射光线与入射光线、法线在同一平面上;反射光线和入射光线位于法线的两侧;反射角等于入射角”为了探清一口深井的底部情况,运用此原理,如图在井口放置一面平面镜可改变光路,当太阳光线与地面所成夹角时,要使太阳光线经反射后刚好垂直于地面射入深井底部,则需要调整平面镜与地面的夹角( )
A. B. C. D.
11.如图,在中,,,,以点为圆心,长为半径画弧,与交于点,再分别以、为圆心,大于的长为半径画弧,两弧交于点、,作直线,分别交、于点、,则的长度为( )
A.
B.
C.
D.
12.如图,等边、等边的边长分别为和开始时点与点重合,在上,在上,沿向右平移,当点到达点时停止.在此过程中,设、重合部分的面积为,移动的距离为,则与的函数图象大致为( )
A. B.
C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.若二次根式有意义,则的取值范围是______.
14.若一元二次方程有两个相等的实数根,则的值为______.
15.如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度单位:与飞行时间单位:之间具有函数关系:,则当小球飞行高度达到最高时,飞行时间______
16.如图,点是矩形中边上一点,沿折叠得到对应的,且点的对应点落在上.若,,则______.
三、解答题:本题共11小题,共66分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:.
18.本小题分
解不等式组:.
19.本小题分
解分式方程:.
20.本小题分
古希腊数学家欧几里得约公元前公元前,被称为“几何学之父”,在其所著的几何原本中第卷给出其中一个命题:如果从圆外的一点向圆引两条直线,一条与圆相切,一条穿过圆,那么被圆截得的线段与该点到凸圆之间的线段为边构成的矩形的面积等于以该点向圆引的切线为边所构成的正方形的面积命题解读:直线为的切线,直线为圆的割线,以为边构造正方形,以,为边构造矩形,可得正方形的面积等于矩形的面积,由此可得.
根据以上问题,完成尺规作图并计算.
尺规作图步骤如下:以点为圆心,小于的长为半径作弧,交射线于,两点;分别以,为圆心,大于的长为半径作弧,两弧交于点;作射线,射线与射线交于点;可得直线为的切线请按描述完成作图;
依据所作图形,若以为边的正方形的面积为,::,则以,为边的矩形的周长为______.
21.本小题分
某学习小组在物理实验结束后,利用实验装置探究几何测量问题.
课题 探究物理实验装置中的几何测量问题
成员 组长:组员:,,
实验工具 测角仪,皮尺,摄像机等
方案一 方案二
测量方案示意图
已知
已知
说明 点为摄像机的位置,小车从同一斜面上相同高度处由静止开始沿斜面下滑,点为小车从斜面到达水平面的位置,点为木块的位置.
测量数据 米,, 米,,.
请选择其中一种方案计算出摄像机机位到小车行驶轴线的竖直距离结果精确到米,参考数据,,
22.本小题分
如图,是的直径,是的弦,平分交于点,过点作的切线,交的延长线于点,交的延长线于点.
求证;
若,,求的长.
23.本小题分
如图,一次函数的图象与反比例函数的图象交于点,.
求反比例函数与一次函数的解析式;
请结合图象直接写出不等式的解集;
若点为轴上一点,的面积为,求点的坐标.
24.本小题分
小红看到一处喷水景观,喷出的水柱呈抛物线形状,她对此展开研究:测得喷水头距地面,水柱在距喷水头水平距离处达到最高,最高点距地面;建立如图所示的平面直角坐标系,并设抛物线的表达式为,其中是水柱距喷水头的水平距离,是水柱距地面的高度.
求抛物线的表达式.
爸爸站在水柱正下方,且距喷水头水平距离身高的小红在水柱下方走动,当她的头顶恰好接触到水柱时,求她与爸爸的水平距离.
25.本小题分
如图,在 中,点,分别在,上,与相交于点,,.
求证:四边形是矩形;
若,,,求四边形的面积.
26.本小题分
问题情境:
在综合实践课上,同学们以“正方形的旋转”为主题开展活动如图,四边形和四边形都是正方形,边长分别是和,将顶点与顶点重合,正方形绕点逆时针方向旋转,连接,.
初步探究:
试猜想线段与的关系,并加以证明;
问题解决:
如图,在正方形的旋转过程中,当点恰好落在边上时,连接,求线段的长;
在图中,若与交于点,请直接写出线段的长.
27.本小题分
【概念学习】
对于平面直角坐标系中的图形和图形,给出如下定义:,分别为图形和图形上任意一点,将,两点间距离的最小值称为图形和图形之间的“关联距离”,记作例如,如图,点与轴之间的“关联距离”轴.
【理解概念】
如图,已知点在边长为的正方形内,则,正方形 ______.
【深入探索】
如图,在等边中,点的坐标是,点,在轴上,点是轴上一点,若,求点的坐标.
【拓展延伸】
已知,,当时,对于每一个,若线段和一次函数是常数,的图象之间的“关联距离”,直线,则的取值范围是______.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:
.
18.解:解不等式得:,
解不等式得:,
则不等式组的解集为.
19.解:去分母得:,
移项得:,
合并同类项得:,
解得:,
检验:把代入得:,
分式方程的解为.
【答案】如图所示;
令,则,
,
以为边的正方形的面积为,
,
,
,
舍去负值,
,,
以,为边的矩形的周长.
21.解:选择方案一:设米,则米,
在中,,
在中,,
,
解得:,
米,
答:摄像机机位到小车行驶轴线的竖直距离约为米.
22.解:证明:连接,
切于,
,
平分,
,
,
,
,
,
;
解:,
∽,
::,
,
,
,,
,
::,
.
23.解:一次函数的图象与反比例函数的图象交于点,.
,
,,
反比例函数解析式为,
点,在一次函数的图象上,
,解得,
一次函数解析式为.
根据函数图象及列函数图象的交点坐标可知,不等式的解集为:或.
在一次函数中,当时,,
,
设点坐标为,则丨丨,
,
解得:或,
或.
24.解:由题意知,抛物线顶点为,
设抛物线的表达式为,将代入得:
,
解得:,
,
答:抛物线的表达式为;
当时,,
解得:或,
她与爸爸的水平距离为或,
答:当她的头顶恰好接触到水柱时,与爸爸的水平距离是或.
25.证明:在 中,,,
,
,
即,
四边形是平行四边形,
,
四边形是矩形;
解:四边形是矩形,
,;
,
勾股定理得;
在中,,
,
由勾股定理得,
,
,
而,
.
26.解:,,
证明:如图,
四边形和四边形是正方形,
,,,
,
,
≌,
,,
延长,相交于点,的延长线交于,
,
,
,
,
,
即,;
在中,,,
根据勾股定理得,,
如图,过点作,交的延长线于,
四边形是正方形,
,,
,
四边形是正方形,
,,
,
,
≌,
,,
,,
,
;
如图,由知,,
四边形是正方形,
,
,
,
由知,,,
,
.
27. 且
【解析】解:与边长为的正方形的边上的点的最小距离为,
根据“关联距离”的定义得:,正方形,
故答案为:;
当在上方时,如图:
,
,
的坐标是,
的坐标是;
当在线段上时,过作于,如图:
,
,
是等边三角形,,
,
,
的坐标是,
,
;
当在下方时,如图:
,
,
;
综上所述,的坐标为或或;
如图:
当时,,
直线过定点,
当时,,,
当时,,,
把代入得:,
解得,
把代入得:,
解得,
线段和一次函数是常数,的图象之间的“关联距离”,直线,
直线与平行四边形无公共点,
由图可知,此时且.
第1页,共1页
同课章节目录
