福建省闽清县天儒中学(人教版)数学九年级上册课件:22.1.4 二次函数y=ax2+bx+c的图象和性质(1)(共37张PPT)
文档属性
| 名称 | 福建省闽清县天儒中学(人教版)数学九年级上册课件:22.1.4 二次函数y=ax2+bx+c的图象和性质(1)(共37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 908.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-06 00:00:00 | ||
图片预览




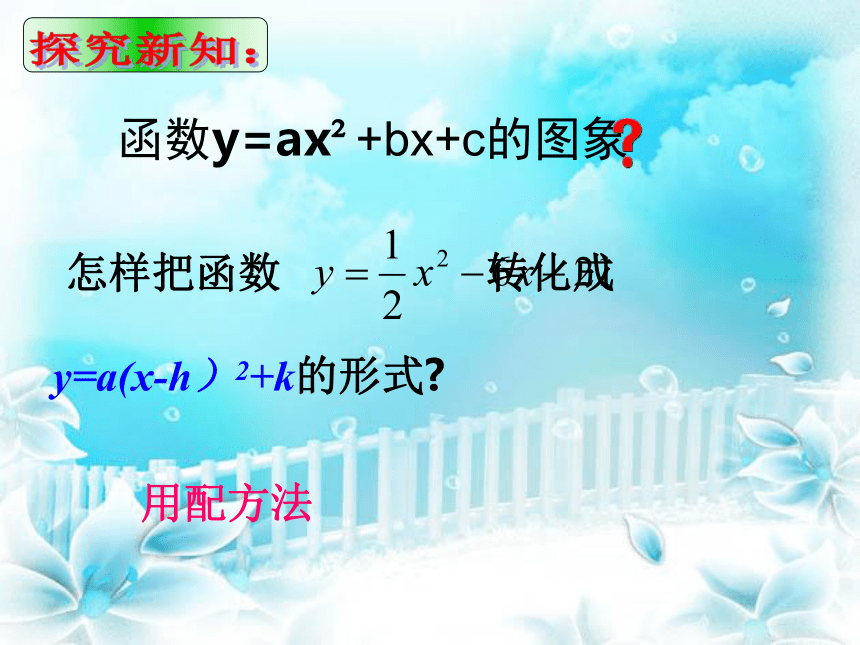




文档简介
课件37张PPT。22.1.4二次函数y=ax2+bx+c
图象和性质(一) 一般地,抛物线y=a(x-h) +k与y=ax 的 相同, 不同22形状位置 y=ax2y=a(x-h) +k2上加下减左加右减知识回顾:抛物线y=a(x-h)2+k有如下特点:
1.当a﹥0时,开口 ,
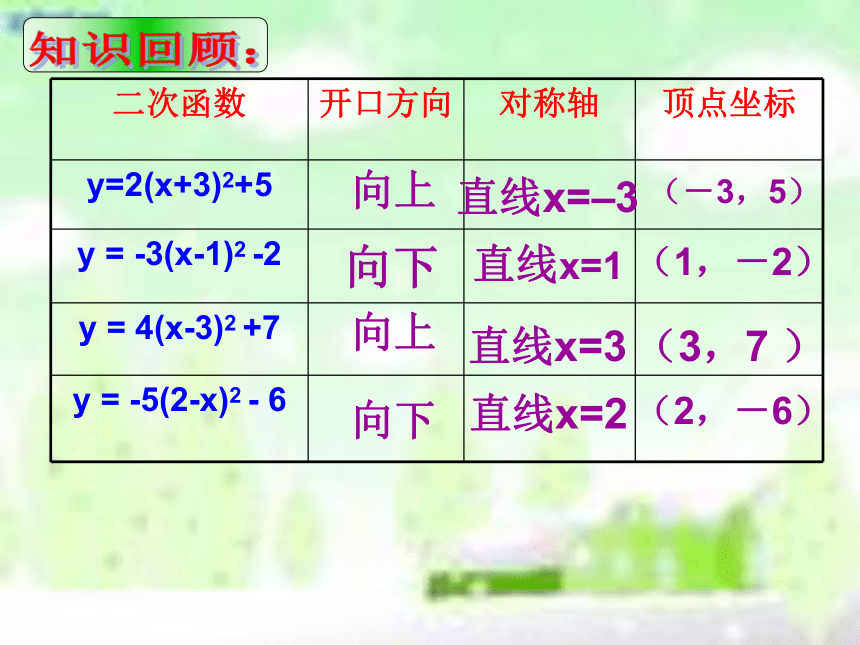
当a﹤0时,开口 ,向上向下 2.对称轴是 ;3.顶点坐标是 。直线X=h(h,k)知识回顾:直线x=–3直线x=1直线x=2直线x=3向上向上向下向下(-3,5)(1,-2)(3,7 )(2,-6)知识回顾:如何画出 的图象呢? 我们知道,像y=a(x-h)2+k这样的函数,容易确定相应抛物线的顶点为(h,k), 二次函数 也 能化成这样的形式吗?创设情境,导入新课:函数y=ax2+bx+c的图象 用配方法探究新知: 怎样把函数 转化成
y=a(x-h)2+k的形式?直接画函数 的图象 提取二次项系数配方整理化简:去掉中括号解:配方 y= — (x―6) +3212你知道是怎样配方的吗? (1)“提”:提出二次项系数;( 2 )“配”:括号内配成完全平方;(3)“化”:化成顶点式。老师提示:
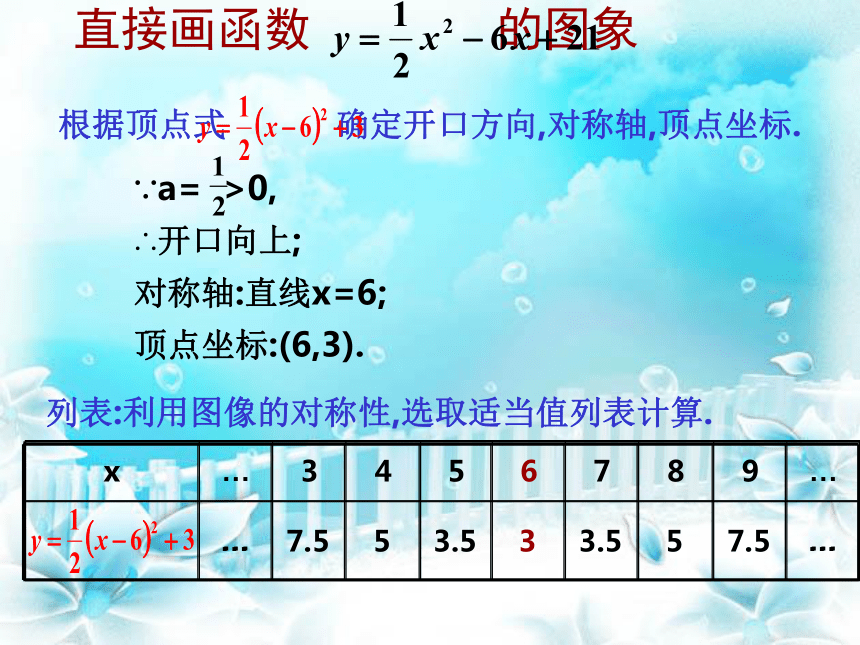
配方后的表达式通常称为配方式或顶点式探究新知:根据顶点式 确定开口方向,对称轴,顶点坐标.列表:利用图像的对称性,选取适当值列表计算.∵a= >0,
∴开口向上;
对称轴:直线x=6;
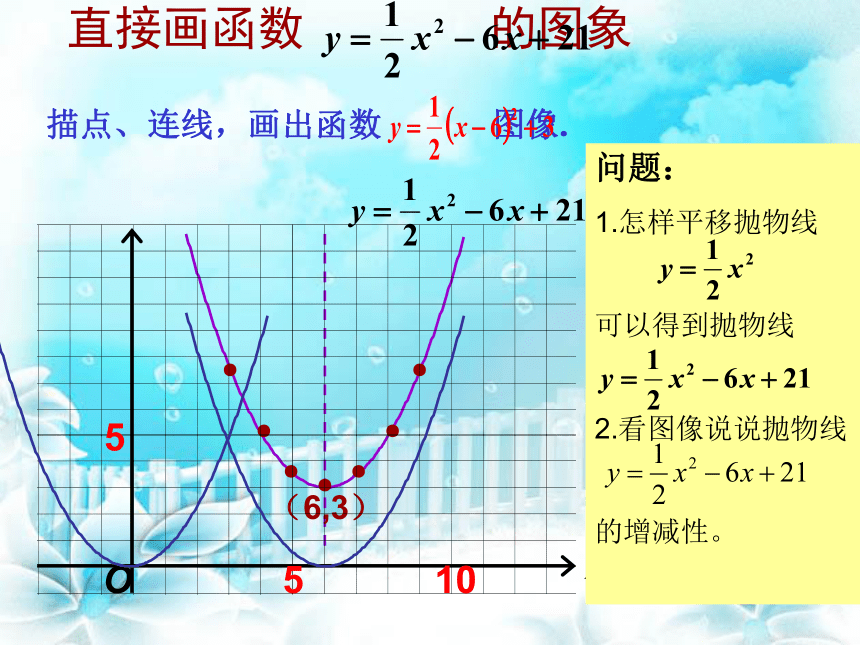
顶点坐标:(6,3).直接画函数 的图象 直接画函数 的图象 描点、连线,画出函数 图像.(6,3)问题:
1.怎样平移抛物线
可以得到抛物线
2.看图像说说抛物线
的增减性。
二次函数 y= —x -6x +21图象的
画法:(1)“化” :化成顶点式 ;(2)“定”:确定开口方向、对称轴、顶
点坐标;(3)“画”:列表、描点、连线。212归纳:探 究 你能用上面的方法讨论二次函数y=-2x2-4x+1的图像和性质吗?求次函数y=ax2+bx+c的对称轴和顶点坐标. 函数y=ax2+bx+c的顶点是配方:提取二次项系数配方:加上再减去一次项系数绝对值一半的平方整理:前三项化为平方形式,后两项合并同类项化简:去掉中括号
这个结果通常称为求顶点坐标公式.问题:因此,抛物线 的对称轴是 顶点
坐标是一般地,我们可以用配方求抛物线 y = ax2 + bx + c (a≠0)的顶点与对称轴方法归纳二次函数y=ax2+bx+c(a≠0)的图象和性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定向上向下在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 根据图形填表:1.写出下列抛物线的开口方向、对称轴及顶点坐标.当x为何值时y的值最小(大)?(4)(3)(2)(1)练习解: (1) a = 3 > 0抛物线开口向上解: a = -1 < 0抛物线开口向下(2)解: a = -2 < 0抛物线开口向下(3)解: a = 0.5 > 0抛物线开口向上(4)练习 已知二次函数y=ax2+bx+c(a≠0)的图像如图所示,在下列5个结论中:
(1)2a-b<0 (2)abc<0 (3)a+b+c>0
(4)a-b+c<0 (5)4a-2b+c>0,正确的有( )
A 1个 B 2个 C 3个 D 4个矩形场地的周长是60m,一边长为l,则另一边长为 ,场地的面积用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长 l 的变化而变化,当 l 是多少时,场地的面积S最大?即 可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是函数的图象的最高点,也就是说,当l取顶点的横坐标时,这个函数有最大值.由公式可求出顶点的横坐标.分析:先写出S与 l 的函数关系式,再求出使S最大的l值.S=l ( 30-l )S=-l 2 +30l( 0 < l < 30 )也就是说, 当l是15m时,场地的面积S最大(S=225m2) 因此,当 时, S有最大 值 ,S=-l 2 +30l( 0 < l < 30 )2.已知直角三角形两条直角边的和等于8,两条直角边各为多少时,这个直角三角形的面积最大,最大值是多少?二次函数y=ax2+bx+c(a≠0)的图象和性质1.位置与开口方向2. 对称轴与顶点坐标3. 最值与增减性抛物线顶点坐标对称轴开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)向上向下在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 根据图形填表:减小 增大 增大 减小 抛物线 位置 平移 平移 知识点1 函数y=ax2+bx+c的图象和性质1.(4分)(2014·成都)将二次函数y=x2-2x+3化为y=(x-h)2+k的形式,结果为( )
A.y=(x+1)2+4 B.y=(x+1)2+2
C.y=(x-1)2+4 D.y=(x-1)2+22.(4分)如图,已知抛物线y=x2+bx+c的对称轴为x=2,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
A.(2,3) B.(4,3)
C.(3,3) D.(3,2)DBx=1 (1,1) 1 (1,-4) 知识点2 二次函数y=ax2+bx+c的平移 左 3 下 2 11 知识点3 抛物线y=ax2+bx+c与系数的关系 8.(4分)如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )B C 一、选择题(每小题5分,共20分)
10.二次函数y=x2-4x+5的最小值是( )
A.-1 B.1 C.3 D.5
11.若一次函数y=ax+b(a≠0)的图象与x轴的交点坐标为(-2,0),则抛物线y=ax2+bx的对称轴为( )
A.直线x=1 B.直线x=-2
C.直线x=-1 D.直线x=4B C 13.已知二次函数y=ax2+bx+c的图象如图,有下列结论:①b2-4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0,其中正确的有( )
A.1个 B.2个 C.3个 D.4个B D 3 >1 -2 三、解答题(共30分)
16.(15分)如图,二次函数y=x2+bx+c的图象与x轴交于A,B两点,且A点坐标为(-3,0),经过B点的直线交抛物线于点D(-2,-3).
(1)求抛物线的解析式和直线BD的解析式;
(2)过x轴上点E(a,0)(E点在B点的右侧)作直线EF∥BD,交抛物线于点F,是否存在实数a使四边形BDFE是平行四边形?如果存在,求出满足条件的a的值;如果不存在,请说明理由.(1)y=x2+2x-3,y=x-1
(2)∵直线BD的解析式为y=x-1,且EF∥BD,∴设直线EF的解析式为y=x+m,若四边形BDFE是平行四边形,则DF∥x轴.∴D,F两点的纵坐标相等,把y=-3代入y=x2+2x-3得x1=-2,x2=0,∴F(0,-3),代入y=x+m,得m=-3,∴y=x-3,令y=0,得x=3,∴E(3,0),即a=3【综合运用】
17.(15分)如图,已知抛物线y=-2x2-4x的图象E,将其向右平移两个单位后得到图象F.
(1)求图象F所表示的抛物线的解析式;
(2)设抛物线F和x轴相交于点O、点B(点B位于点O的右侧),顶点为点C,点A位于y轴负半轴上,且到x轴的距离等于点C到x轴的距离的2倍,求AB所在直线的解析式.
图象和性质(一) 一般地,抛物线y=a(x-h) +k与y=ax 的 相同, 不同22形状位置 y=ax2y=a(x-h) +k2上加下减左加右减知识回顾:抛物线y=a(x-h)2+k有如下特点:
1.当a﹥0时,开口 ,
当a﹤0时,开口 ,向上向下 2.对称轴是 ;3.顶点坐标是 。直线X=h(h,k)知识回顾:直线x=–3直线x=1直线x=2直线x=3向上向上向下向下(-3,5)(1,-2)(3,7 )(2,-6)知识回顾:如何画出 的图象呢? 我们知道,像y=a(x-h)2+k这样的函数,容易确定相应抛物线的顶点为(h,k), 二次函数 也 能化成这样的形式吗?创设情境,导入新课:函数y=ax2+bx+c的图象 用配方法探究新知: 怎样把函数 转化成
y=a(x-h)2+k的形式?直接画函数 的图象 提取二次项系数配方整理化简:去掉中括号解:配方 y= — (x―6) +3212你知道是怎样配方的吗? (1)“提”:提出二次项系数;( 2 )“配”:括号内配成完全平方;(3)“化”:化成顶点式。老师提示:
配方后的表达式通常称为配方式或顶点式探究新知:根据顶点式 确定开口方向,对称轴,顶点坐标.列表:利用图像的对称性,选取适当值列表计算.∵a= >0,
∴开口向上;
对称轴:直线x=6;
顶点坐标:(6,3).直接画函数 的图象 直接画函数 的图象 描点、连线,画出函数 图像.(6,3)问题:
1.怎样平移抛物线
可以得到抛物线
2.看图像说说抛物线
的增减性。
二次函数 y= —x -6x +21图象的
画法:(1)“化” :化成顶点式 ;(2)“定”:确定开口方向、对称轴、顶
点坐标;(3)“画”:列表、描点、连线。212归纳:探 究 你能用上面的方法讨论二次函数y=-2x2-4x+1的图像和性质吗?求次函数y=ax2+bx+c的对称轴和顶点坐标. 函数y=ax2+bx+c的顶点是配方:提取二次项系数配方:加上再减去一次项系数绝对值一半的平方整理:前三项化为平方形式,后两项合并同类项化简:去掉中括号
这个结果通常称为求顶点坐标公式.问题:因此,抛物线 的对称轴是 顶点
坐标是一般地,我们可以用配方求抛物线 y = ax2 + bx + c (a≠0)的顶点与对称轴方法归纳二次函数y=ax2+bx+c(a≠0)的图象和性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定向上向下在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 根据图形填表:1.写出下列抛物线的开口方向、对称轴及顶点坐标.当x为何值时y的值最小(大)?(4)(3)(2)(1)练习解: (1) a = 3 > 0抛物线开口向上解: a = -1 < 0抛物线开口向下(2)解: a = -2 < 0抛物线开口向下(3)解: a = 0.5 > 0抛物线开口向上(4)练习 已知二次函数y=ax2+bx+c(a≠0)的图像如图所示,在下列5个结论中:
(1)2a-b<0 (2)abc<0 (3)a+b+c>0
(4)a-b+c<0 (5)4a-2b+c>0,正确的有( )
A 1个 B 2个 C 3个 D 4个矩形场地的周长是60m,一边长为l,则另一边长为 ,场地的面积用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长 l 的变化而变化,当 l 是多少时,场地的面积S最大?即 可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是函数的图象的最高点,也就是说,当l取顶点的横坐标时,这个函数有最大值.由公式可求出顶点的横坐标.分析:先写出S与 l 的函数关系式,再求出使S最大的l值.S=l ( 30-l )S=-l 2 +30l( 0 < l < 30 )也就是说, 当l是15m时,场地的面积S最大(S=225m2) 因此,当 时, S有最大 值 ,S=-l 2 +30l( 0 < l < 30 )2.已知直角三角形两条直角边的和等于8,两条直角边各为多少时,这个直角三角形的面积最大,最大值是多少?二次函数y=ax2+bx+c(a≠0)的图象和性质1.位置与开口方向2. 对称轴与顶点坐标3. 最值与增减性抛物线顶点坐标对称轴开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)向上向下在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 根据图形填表:减小 增大 增大 减小 抛物线 位置 平移 平移 知识点1 函数y=ax2+bx+c的图象和性质1.(4分)(2014·成都)将二次函数y=x2-2x+3化为y=(x-h)2+k的形式,结果为( )
A.y=(x+1)2+4 B.y=(x+1)2+2
C.y=(x-1)2+4 D.y=(x-1)2+22.(4分)如图,已知抛物线y=x2+bx+c的对称轴为x=2,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
A.(2,3) B.(4,3)
C.(3,3) D.(3,2)DBx=1 (1,1) 1 (1,-4) 知识点2 二次函数y=ax2+bx+c的平移 左 3 下 2 11 知识点3 抛物线y=ax2+bx+c与系数的关系 8.(4分)如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )B C 一、选择题(每小题5分,共20分)
10.二次函数y=x2-4x+5的最小值是( )
A.-1 B.1 C.3 D.5
11.若一次函数y=ax+b(a≠0)的图象与x轴的交点坐标为(-2,0),则抛物线y=ax2+bx的对称轴为( )
A.直线x=1 B.直线x=-2
C.直线x=-1 D.直线x=4B C 13.已知二次函数y=ax2+bx+c的图象如图,有下列结论:①b2-4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0,其中正确的有( )
A.1个 B.2个 C.3个 D.4个B D 3 >1 -2 三、解答题(共30分)
16.(15分)如图,二次函数y=x2+bx+c的图象与x轴交于A,B两点,且A点坐标为(-3,0),经过B点的直线交抛物线于点D(-2,-3).
(1)求抛物线的解析式和直线BD的解析式;
(2)过x轴上点E(a,0)(E点在B点的右侧)作直线EF∥BD,交抛物线于点F,是否存在实数a使四边形BDFE是平行四边形?如果存在,求出满足条件的a的值;如果不存在,请说明理由.(1)y=x2+2x-3,y=x-1
(2)∵直线BD的解析式为y=x-1,且EF∥BD,∴设直线EF的解析式为y=x+m,若四边形BDFE是平行四边形,则DF∥x轴.∴D,F两点的纵坐标相等,把y=-3代入y=x2+2x-3得x1=-2,x2=0,∴F(0,-3),代入y=x+m,得m=-3,∴y=x-3,令y=0,得x=3,∴E(3,0),即a=3【综合运用】
17.(15分)如图,已知抛物线y=-2x2-4x的图象E,将其向右平移两个单位后得到图象F.
(1)求图象F所表示的抛物线的解析式;
(2)设抛物线F和x轴相交于点O、点B(点B位于点O的右侧),顶点为点C,点A位于y轴负半轴上,且到x轴的距离等于点C到x轴的距离的2倍,求AB所在直线的解析式.
同课章节目录
