福建省闽清县天儒中学(人教版)数学九年级上册课件:22.2用函数观点看一元二次方程(共28张PPT)
文档属性
| 名称 | 福建省闽清县天儒中学(人教版)数学九年级上册课件:22.2用函数观点看一元二次方程(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 664.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-06 00:00:00 | ||
图片预览







文档简介
课件28张PPT。二次函数与一元二次方程二次函数与x轴的交点一、探究探究1、求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标.解:∵A、B在x轴上,
∴它们的纵坐标为0,
∴令y=0,则x2-3x+2=0
解得:x1=1,x2=2;
∴A(1,0) , B(2,0)你发现方程 的解x1、x2与A、B的坐标有什么联系?
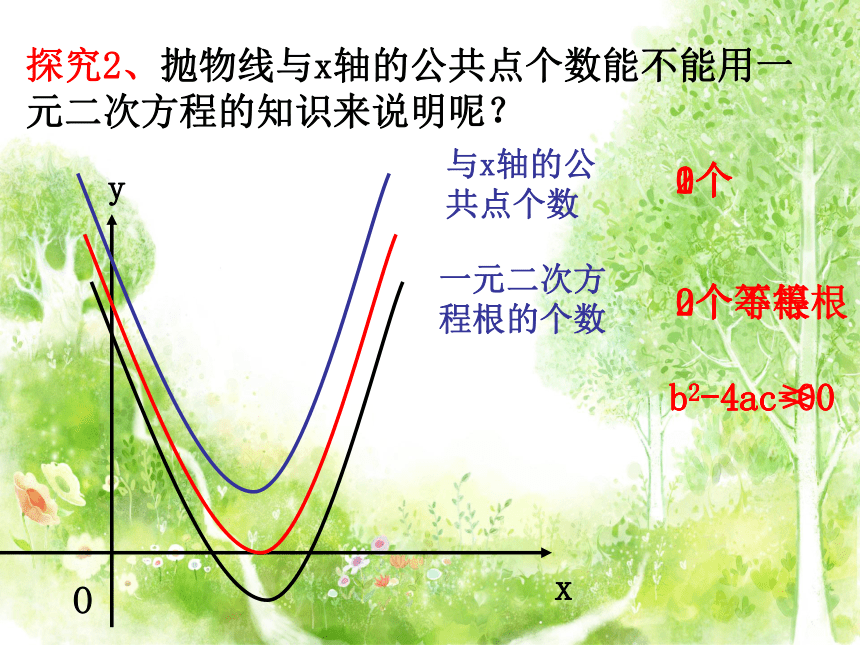
x2-3x+2=0结论1:方程x2-3x+2=0的解就是抛物线y=x2-3x+2与x轴的两个交点的横坐标.因此,抛物线与一元二次方程是有密切联系的.即:若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A( ), B( )x1,0x2,0x探究2、抛物线与x轴的公共点个数能不能用一元二次方程的知识来说明呢?Oxy与x轴的公共点个数一元二次方程根的个数2个2个不等根b2-4ac>01个2个等根0个0个b2-4ac<0b2-4ac=0一元二次方程ax2+bx+c=0有两个不等的实数根结论2:抛物线y=ax2+bx+c与x轴有两个公共点抛物线y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况说明:抛物线y=ax2+bx+c与x轴有唯一公共点一元二次方程ax2+bx+c=0有两个相等的实数根抛物线y=ax2+bx+c与x轴没有公共点一元二次方程ax2+bx+c=0没有实数根 1、b2-4ac>0 2、 b2-4ac =0 3、 b2-4ac <0 1、下列各抛物线与x轴是否有公共点,如果有,求出公共点的坐标.
(1)y=6x2-2x+1
(2)y=-15x2+14x+8
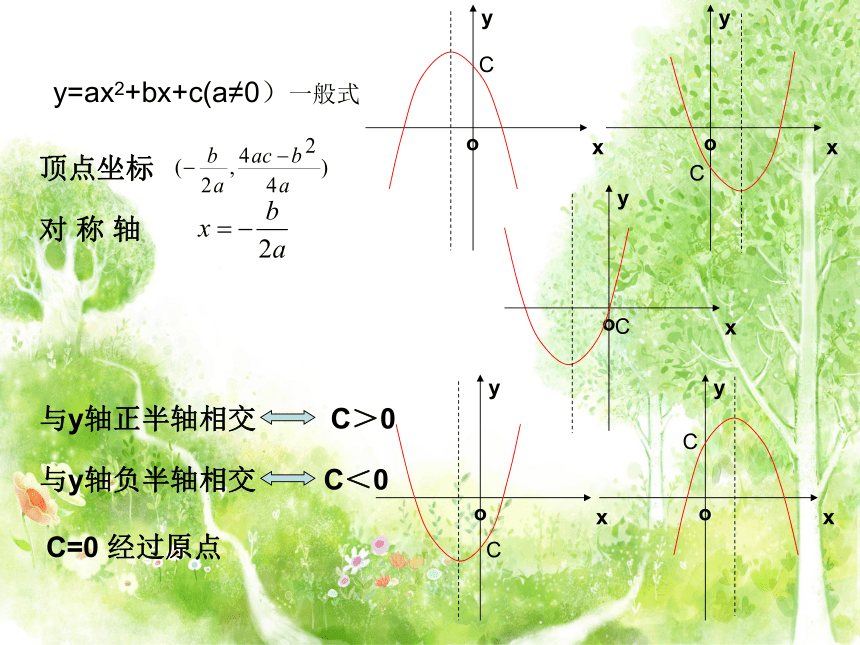
(3)y=x2-4x+4关键:令y=0时,看b2-4ac.二、基础训练二次函数与y轴的交点y=ax2+bx+c(a≠0)一般式C>0C<0C=0 经过原点顶点坐标对 称 轴与y轴正半轴相交
与y轴负半轴相交
与y轴交点的求法:令x=0,得到y=c 即(0,c)与y轴始终有一个交点(0,c)如果y=ax2+bx+c的图象与x轴的交点为A(x1,0),B(x2,0);
那么AB=|x1-x2|=二次函数顶点位置顶点在y轴上 顶点在x轴上 顶点在原点b=c=02、判断下列各抛物线与坐标轴的交点个数.
(1)y=6x2-2x+1 (2)y=2x2-6x基础训练3、已知抛物线y=x2-6x+a的顶点在x轴上,则a= ;若抛物线与x轴有两个交点,则a的范围是 ;若抛物线与坐标轴有两个公共点,则a= ;顶点在x轴上b2-4ac=0与x轴有两个交点方程有两个不等实根9a<99或0 基础训练4、已知抛物线y=x2-3x+a+1与x轴最多只有
一个公共点,则a的范围是 .5、关于x的方程x2-x-n=0没有实数根,则抛物
线y=x2-x-n的顶点在 象限.第一基础训练1、已知抛物线y=x2+2x+m+1与x轴只有一个公共点,求m的值.
三、例题分析:2、求证:不论k取何值时,抛物线y=x2-kx-2+k与x轴总有两个不同的交点.
例题分析:3、抛物线y=-x2-x+12如图所示oyxA(-4,0)B(3,0)y=-x2-x+12x 时,y>0.x 时,
y<0.-4 论x取何值时,函数y的值都是非负数.
求:m的取值范围.例题分析: 函数值为正值图像在x轴上方联想:二次函数与x轴的交点个数可以借助判别式解决,那么二次函数与一次函数的交点个数又该怎么解决呢?
例如,二次函数y=x2-2x-3和一次函数y=x+2有交点吗?有几个?
分析:两个函数的交点是这两个函数的公共解,先列出方程组,消去y后,再利用判别式判断即可.例题分析
5.二次函数y=x2-x-3和一次函数y=x+b有一个公共点(即相切),求出b的值.
解:由题意,得
消元,得 x2-x-3 =x+b
整理,得x2-2x -(3 + b) =0
∵有唯一交点
∴(-2)2 +4( 3 + b) =0
解之得,b =-4y=x2-x-3y=x+b 6、 已知:抛物线y=ax2+bx+c的图象如图所示:
(1)求此抛物线的解析式;
(2)当x取何值时,y>0?
(3)将抛物线作怎样的一次
平移,才能使它与坐标轴仅有
两个交点,并写出此时抛物线
的解析式.xyoABDC-15-2.5y= (x+1)(x-5)= (x-2)2 -例题分析:xyoABDC-15-2.5 6、 已知:抛物线y=ax2+bx+c的图象如图所示:
(1)求此抛物线的解析式;
(2)当x取何值时,y>0?
(3)将抛物线作怎样的一次
平移,才能使它与坐标轴仅有
两个交点,并写出此时抛物线
的解析式.例题分析:y= (x+1)(x-5)= (x-2)2-xyoABDC-15-2.5 6、 已知:抛物线y=ax2+bx+c的图象如图所示:
(1)求此抛物线的解析式;
(2)当x取何值时,y>0?
(3)将抛物线作怎样的一次
平移,才能使它与坐标轴仅有
两个交点,并写出此时抛物线
的解析式.例题分析:y= (x+1)(x-5)= (x-2)2-xyoABDC-15-2.5 6、 已知:抛物线y=ax2+bx+c的图象如图所示:
(1)求此抛物线的解析式;
(2)当x取何值时,y>0?
(3)将抛物线作怎样的一次
平移,才能使它与坐标轴仅有
两个交点,并写出此时抛物线
的解析式.例题分析:y= (x+1)(x-5)= (x-2)2-四、小结1、若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A(x1,0 ), B( x2,0 )
2、若一元二次方程ax2+bx+c=0与二次三项式ax2+bx+c及二次函数y=ax2+bx+c这三个“二次”之间互相转化的关系.体现了数形结合的思想.二次函数与一元二次方程3.二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?有两个交点有两个相异的实数根b2-4ac > 0有一个交点有两个相等的实数根b2-4ac = 0没有交点没有实数根b2-4ac < 0四、小结
∴它们的纵坐标为0,
∴令y=0,则x2-3x+2=0
解得:x1=1,x2=2;
∴A(1,0) , B(2,0)你发现方程 的解x1、x2与A、B的坐标有什么联系?
x2-3x+2=0结论1:方程x2-3x+2=0的解就是抛物线y=x2-3x+2与x轴的两个交点的横坐标.因此,抛物线与一元二次方程是有密切联系的.即:若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A( ), B( )x1,0x2,0x探究2、抛物线与x轴的公共点个数能不能用一元二次方程的知识来说明呢?Oxy与x轴的公共点个数一元二次方程根的个数2个2个不等根b2-4ac>01个2个等根0个0个b2-4ac<0b2-4ac=0一元二次方程ax2+bx+c=0有两个不等的实数根结论2:抛物线y=ax2+bx+c与x轴有两个公共点抛物线y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况说明:抛物线y=ax2+bx+c与x轴有唯一公共点一元二次方程ax2+bx+c=0有两个相等的实数根抛物线y=ax2+bx+c与x轴没有公共点一元二次方程ax2+bx+c=0没有实数根 1、b2-4ac>0 2、 b2-4ac =0 3、 b2-4ac <0 1、下列各抛物线与x轴是否有公共点,如果有,求出公共点的坐标.
(1)y=6x2-2x+1
(2)y=-15x2+14x+8
(3)y=x2-4x+4关键:令y=0时,看b2-4ac.二、基础训练二次函数与y轴的交点y=ax2+bx+c(a≠0)一般式C>0C<0C=0 经过原点顶点坐标对 称 轴与y轴正半轴相交
与y轴负半轴相交
与y轴交点的求法:令x=0,得到y=c 即(0,c)与y轴始终有一个交点(0,c)如果y=ax2+bx+c的图象与x轴的交点为A(x1,0),B(x2,0);
那么AB=|x1-x2|=二次函数顶点位置顶点在y轴上 顶点在x轴上 顶点在原点b=c=02、判断下列各抛物线与坐标轴的交点个数.
(1)y=6x2-2x+1 (2)y=2x2-6x基础训练3、已知抛物线y=x2-6x+a的顶点在x轴上,则a= ;若抛物线与x轴有两个交点,则a的范围是 ;若抛物线与坐标轴有两个公共点,则a= ;顶点在x轴上b2-4ac=0与x轴有两个交点方程有两个不等实根9a<99或0 基础训练4、已知抛物线y=x2-3x+a+1与x轴最多只有
一个公共点,则a的范围是 .5、关于x的方程x2-x-n=0没有实数根,则抛物
线y=x2-x-n的顶点在 象限.第一基础训练1、已知抛物线y=x2+2x+m+1与x轴只有一个公共点,求m的值.
三、例题分析:2、求证:不论k取何值时,抛物线y=x2-kx-2+k与x轴总有两个不同的交点.
例题分析:3、抛物线y=-x2-x+12如图所示oyxA(-4,0)B(3,0)y=-x2-x+12x 时,y>0.x 时,
y<0.-4
求:m的取值范围.例题分析: 函数值为正值图像在x轴上方联想:二次函数与x轴的交点个数可以借助判别式解决,那么二次函数与一次函数的交点个数又该怎么解决呢?
例如,二次函数y=x2-2x-3和一次函数y=x+2有交点吗?有几个?
分析:两个函数的交点是这两个函数的公共解,先列出方程组,消去y后,再利用判别式判断即可.例题分析
5.二次函数y=x2-x-3和一次函数y=x+b有一个公共点(即相切),求出b的值.
解:由题意,得
消元,得 x2-x-3 =x+b
整理,得x2-2x -(3 + b) =0
∵有唯一交点
∴(-2)2 +4( 3 + b) =0
解之得,b =-4y=x2-x-3y=x+b 6、 已知:抛物线y=ax2+bx+c的图象如图所示:
(1)求此抛物线的解析式;
(2)当x取何值时,y>0?
(3)将抛物线作怎样的一次
平移,才能使它与坐标轴仅有
两个交点,并写出此时抛物线
的解析式.xyoABDC-15-2.5y= (x+1)(x-5)= (x-2)2 -例题分析:xyoABDC-15-2.5 6、 已知:抛物线y=ax2+bx+c的图象如图所示:
(1)求此抛物线的解析式;
(2)当x取何值时,y>0?
(3)将抛物线作怎样的一次
平移,才能使它与坐标轴仅有
两个交点,并写出此时抛物线
的解析式.例题分析:y= (x+1)(x-5)= (x-2)2-xyoABDC-15-2.5 6、 已知:抛物线y=ax2+bx+c的图象如图所示:
(1)求此抛物线的解析式;
(2)当x取何值时,y>0?
(3)将抛物线作怎样的一次
平移,才能使它与坐标轴仅有
两个交点,并写出此时抛物线
的解析式.例题分析:y= (x+1)(x-5)= (x-2)2-xyoABDC-15-2.5 6、 已知:抛物线y=ax2+bx+c的图象如图所示:
(1)求此抛物线的解析式;
(2)当x取何值时,y>0?
(3)将抛物线作怎样的一次
平移,才能使它与坐标轴仅有
两个交点,并写出此时抛物线
的解析式.例题分析:y= (x+1)(x-5)= (x-2)2-四、小结1、若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A(x1,0 ), B( x2,0 )
2、若一元二次方程ax2+bx+c=0与二次三项式ax2+bx+c及二次函数y=ax2+bx+c这三个“二次”之间互相转化的关系.体现了数形结合的思想.二次函数与一元二次方程3.二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?有两个交点有两个相异的实数根b2-4ac > 0有一个交点有两个相等的实数根b2-4ac = 0没有交点没有实数根b2-4ac < 0四、小结
同课章节目录
