福建省闽清县天儒中学(人教版)数学九年级上册课件:22-3二次函数与面积问题(共25张PPT)
文档属性
| 名称 | 福建省闽清县天儒中学(人教版)数学九年级上册课件:22-3二次函数与面积问题(共25张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 440.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-06 00:00:00 | ||
图片预览





文档简介
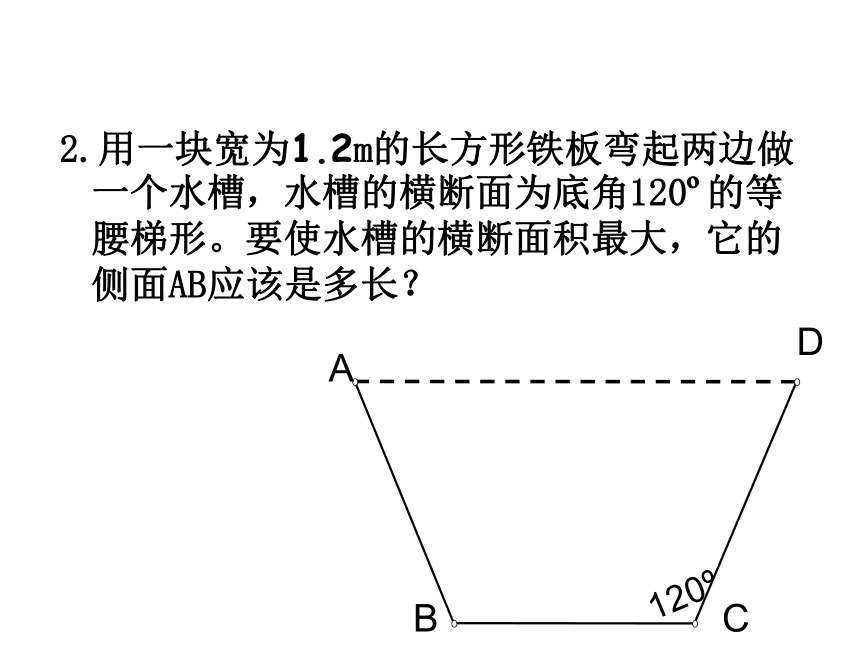
课件25张PPT。 (1) 请用长20米的篱笆设计一个矩形的菜园。(2)怎样设计才能使矩形菜园的面积最大?
(0自变量的取值范围; (2)怎样围才能使菜园的面积最大?
最大面积是多少?
如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。 解: (1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为(24-4x)米
(3) ∵墙的可用长度为8米
(2)当x= 时,S最大值= =36(平方米)∴ S=x(24-4x)
=-4x2+24 x (0∴ 0<24-4x ≤6 4≤x<6∴当x=4cm时,S最大值=32 平方米1.某工厂为了存放材料,需要围一个周长160米的矩形场地,问矩形的长和宽各取多少米,才能使存放场地的面积最大。练一练:2.用一块宽为1.2m的长方形铁板弯起两边做一个水槽,水槽的横断面为底角120o的等腰梯形。要使水槽的横断面积最大,它的侧面AB应该是多长?
巩固2、如图,正方形ABCD的边长是4,
E是AB上一点,F是AD延长线上一点,
BE=DF。四边形AEGF是矩形,则矩
形AEGF的面积y随BE的长x的变化而
变化,y与x之间可
以用怎样的函数来
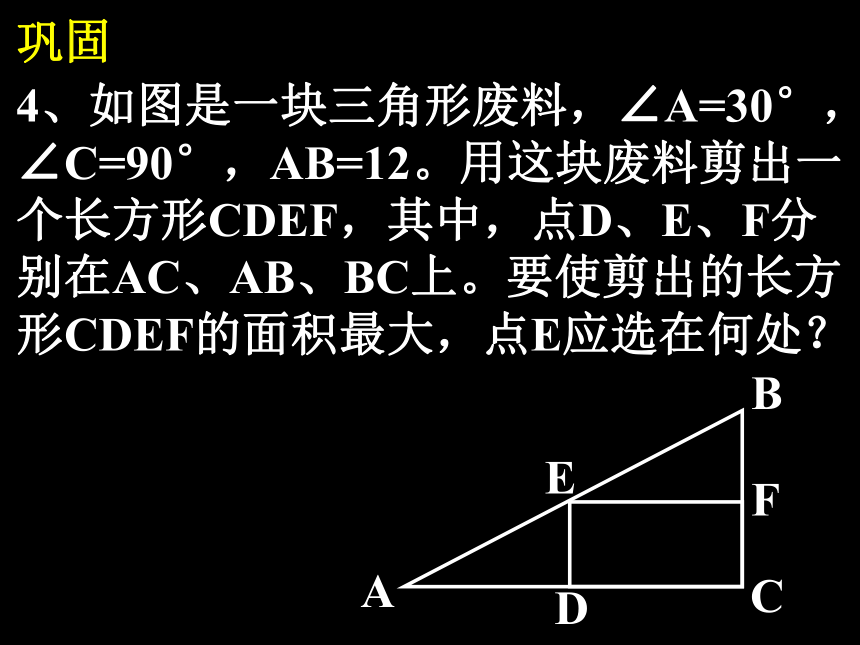
表示?巩固4、如图是一块三角形废料,∠A=30°,
∠C=90°,AB=12。用这块废料剪出一
个长方形CDEF,其中,点D、E、F分
别在AC、AB、BC上。要使剪出的长方
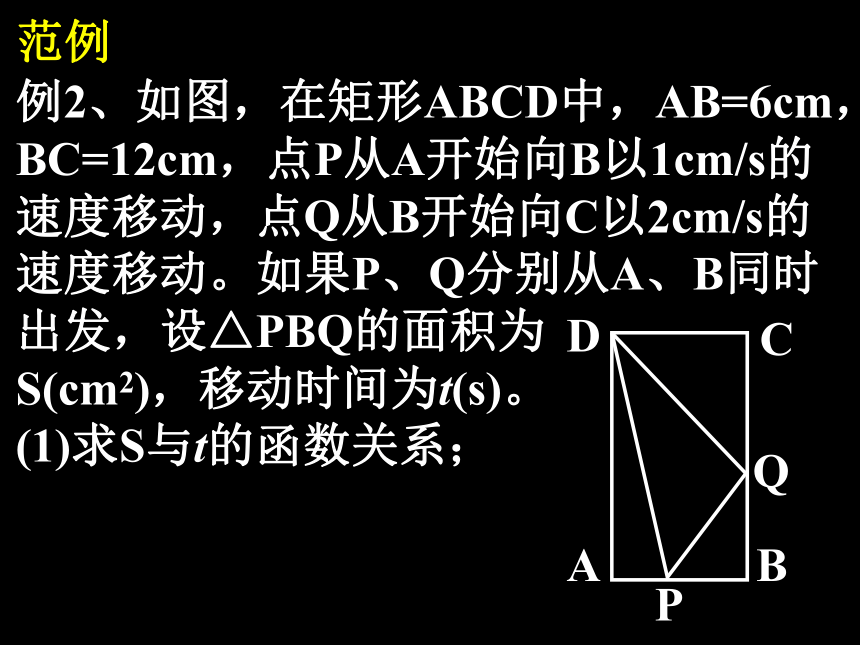
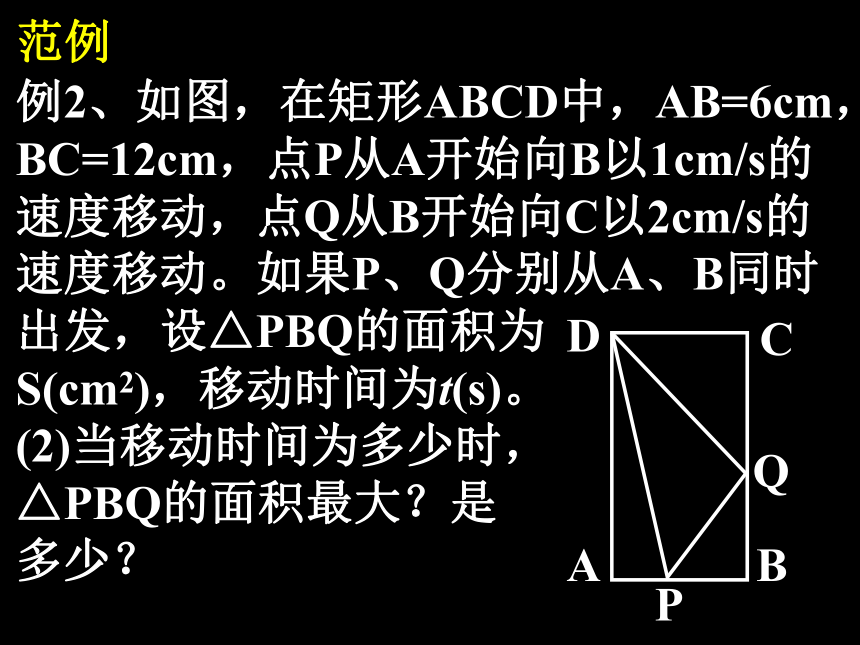
形CDEF的面积最大,点E应选在何处?范例例2、如图,在矩形ABCD中,AB=6cm,
BC=12cm,点P从A开始向B以1cm/s的
速度移动,点Q从B开始向C以2cm/s的
速度移动。如果P、Q分别从A、B同时
出发,设△PBQ的面积为
S(cm2),移动时间为t(s)。
(1)求S与t的函数关系;范例例2、如图,在矩形ABCD中,AB=6cm,
BC=12cm,点P从A开始向B以1cm/s的
速度移动,点Q从B开始向C以2cm/s的
速度移动。如果P、Q分别从A、B同时
出发,设△PBQ的面积为
S(cm2),移动时间为t(s)。
(2)当移动时间为多少时,
△PBQ的面积最大?是
多少?巩固3、如图,△ABC中,∠B=90°,AB=
6cm,BC=12cm,点P从A开始沿AB边
向B以1cm/s的速度移动;点Q从B开始
沿BC边向C以2cm/s的速度移动。如果
P、Q同时出发,问经过几秒钟,
△PQB的面积最大?最大面积
是多少?(1).设矩形的一边BC=xm,那么AB边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少?何时面积最大 如图,在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上.xmbm4.如图3,规格为60 cm×60 cm的正方形地砖在运输过程中受损,断去一角,量得AF=30cm,CE=45 cm。现准备从五边形地砖ABCEF上截出一个面积为S的矩形地砖PMBN。
(1)设BN=x,BM=y,请用含x的代数式表示y,并写出x的取值范围;
(2)请用含x的代数式表示S,并在给定的直角坐标系内画出该函数的示意图;
(3)利用函数图象回2答:当x取何值时,S有最大值?最大值是多少? 图35.在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/秒的速度移动,同时,点Q从点B出发沿BC边向点C以2cm/秒的速度移动。如果P、Q两点在分别到达B、C两点后就停止移动,回答下列问题:
(1)运动开始后第几秒时, △PBQ的面积等于8cm2
(2)设运动开始后第t秒时, 五边形APQCD的面积为Scm2, 写出S与t的函数关系式, 并指出自变量t的取值范围;
t为何值时S最小?求出S的最小值。 6.如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方). (1)求A、B两点的坐标;(2)设△OMN的面积为S,直线l运动时间为t秒(0≤t≤6),试求S 与t的函数表达式;(3)在题(2)的条件下,t为何值时,S的面积最大?最大面积是多少? 7.二次函数y=ax +bx+c的图象的一部分如图所示,已知它的顶点M在第二象限,且经过点A(1,0)和点B(0,1)。
(1)请判断实数a的取值范围,并说明理由;2xy1B1AO-1<a<0例2:有一根直尺的短边长2cm,长边长10cm,还有一块锐角为45°的直角三角形纸板,其中直角三角形纸板的斜边长为12cm.按图14—1的方式将直尺的短边DE放置在与直角三角形纸板的斜边AB上,且点D与点A重合.若直尺沿射线AB方向平行移动,如图14—2,设平移的长度为x(cm),直尺和三角形纸板的重叠部分(图中阴影部分)的面积为S cm 2).
(1)当x=0时,S=_____________;
当x = 10时,S =______________;
(2)当0<x≤4时,如图14—2,求S与x的函数关系式;
(3)当6<x<10时,求S与x的函数关系式;
(4)请你作出推测:当x为何值时,阴影部分的面积最大?并写出最大值.zxxkwA知识点1:用配方法或公式法求二次函数的最大(小)值
1.当-2≤x≤3时,二次函数y=x2-2x+3的最大值为_______,最小值为________.
知识点2:二次函数与图形面积问题
2.在一幅长60 cm,宽40 cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图(如图),如果要使整个挂图的面积是y cm2,设金色纸边的宽度为x cm,那么y与x之间的函数关系是( )
A.y=(60+2x)(40+2x)
B.y=(60+x)(40+x)
C.y=(60+2x)(40+x)
D.y=(60+x)(40+2x)112B 20m 第4题图 第5题图 C 800m2 6.如图,在△ABC中,∠B=90°,AB=8 cm,BC=6 cm,点P从点A开始沿AB向B点以2 cm/s的速度移动,点Q从点B开始沿BC向C点以1 cm/s的速度移动,如果P,Q分别同时出发,当△PBQ的面积为最大时,运动时间t为_______s.
7.小磊要制作一个三角形的钢架模型,在这个三角形中,长度为x(单位:cm)的边与这条边上的高之和为40 cm,这个三角形的面积S(单位:cm2)随x的变化而变化.
(1)S与x之间的函数关系式为____________________;
(2)当x=_______时,这个三角形面积S最大,最大面积是__________.220cm200cm28.如图,一个正方形纸板的边长为10 cm,将它割去一个正方形,留下四个全等的直角三角形(图中阴影部分).设AE=BF=CG=DH=x(cm),阴影部分的面积为y(cm2).
(1)求y关于x的函数解析式和自变量的取值范围;
(2)当x取何值时,阴影部分的面积达到最大,最大值为多少?解:(1)y=-2x2+20x(0<x<10) (2)配方得y=-2(x-5)2+50,
∴当x=5时,阴影面积最大,y最大=5012.5cm2 6cm (1)请直接写出S与x之间的函数关系式;(不要求写出自变量x的取值范围)
(2)当x是多少时,菱形风筝面积S最大?最大面积是多少?12.(2014·成都)在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x m.
(1)若花园的面积为192 m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15 m和6 m,
要将这棵树围在花园内(含边界,不考虑树的粗细),
求花园面积S的最大值.解:(1)由AB=x,得BC=28-x,根据题意, 得x(28-x)=192,解得x1=12,x2=16
(2)S=x(28-x)=-x2+28x=-(x-14)2+196,∵x≥6,
28-x≥15,∴6≤x≤13.∵a=-1<0,∴当6≤x≤13时,S随x的增大而增大,∴当x=13时,S有最大值195 m213.如图,等腰直角三角形ABC以2 cm/s的速度沿直线m匀速向正方形CDEF移动,直到AB与EF重合.设移动x s时,三角形与正方形重合部分的面积为y cm2.(1)当x=2,7时,y的值分别为多少?
(2)求从开始移动时到AB与EF重合时,
y与x的函数关系式,并求出x的取值范围.解:(1)当x=2时,y=8;当x=7时,y=421.理解问题;“二次函数应用” 的思路 回顾上一节“最大利润”和本节“最大面积”解决问题的过程,你能总结一下解决此类问题的基本思路吗?与同伴交流.2.分析问题中的变量和常量,以及它们之间的关系;3.用数学的方式表示出它们之间的关系;4.做数学求解;5.检验结果的合理性,拓展等.
(0
最大面积是多少?
如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。 解: (1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为(24-4x)米
(3) ∵墙的可用长度为8米
(2)当x= 时,S最大值= =36(平方米)∴ S=x(24-4x)
=-4x2+24 x (0
巩固2、如图,正方形ABCD的边长是4,
E是AB上一点,F是AD延长线上一点,
BE=DF。四边形AEGF是矩形,则矩
形AEGF的面积y随BE的长x的变化而
变化,y与x之间可
以用怎样的函数来
表示?巩固4、如图是一块三角形废料,∠A=30°,
∠C=90°,AB=12。用这块废料剪出一
个长方形CDEF,其中,点D、E、F分
别在AC、AB、BC上。要使剪出的长方
形CDEF的面积最大,点E应选在何处?范例例2、如图,在矩形ABCD中,AB=6cm,
BC=12cm,点P从A开始向B以1cm/s的
速度移动,点Q从B开始向C以2cm/s的
速度移动。如果P、Q分别从A、B同时
出发,设△PBQ的面积为
S(cm2),移动时间为t(s)。
(1)求S与t的函数关系;范例例2、如图,在矩形ABCD中,AB=6cm,
BC=12cm,点P从A开始向B以1cm/s的
速度移动,点Q从B开始向C以2cm/s的
速度移动。如果P、Q分别从A、B同时
出发,设△PBQ的面积为
S(cm2),移动时间为t(s)。
(2)当移动时间为多少时,
△PBQ的面积最大?是
多少?巩固3、如图,△ABC中,∠B=90°,AB=
6cm,BC=12cm,点P从A开始沿AB边
向B以1cm/s的速度移动;点Q从B开始
沿BC边向C以2cm/s的速度移动。如果
P、Q同时出发,问经过几秒钟,
△PQB的面积最大?最大面积
是多少?(1).设矩形的一边BC=xm,那么AB边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少?何时面积最大 如图,在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上.xmbm4.如图3,规格为60 cm×60 cm的正方形地砖在运输过程中受损,断去一角,量得AF=30cm,CE=45 cm。现准备从五边形地砖ABCEF上截出一个面积为S的矩形地砖PMBN。
(1)设BN=x,BM=y,请用含x的代数式表示y,并写出x的取值范围;
(2)请用含x的代数式表示S,并在给定的直角坐标系内画出该函数的示意图;
(3)利用函数图象回2答:当x取何值时,S有最大值?最大值是多少? 图35.在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/秒的速度移动,同时,点Q从点B出发沿BC边向点C以2cm/秒的速度移动。如果P、Q两点在分别到达B、C两点后就停止移动,回答下列问题:
(1)运动开始后第几秒时, △PBQ的面积等于8cm2
(2)设运动开始后第t秒时, 五边形APQCD的面积为Scm2, 写出S与t的函数关系式, 并指出自变量t的取值范围;
t为何值时S最小?求出S的最小值。 6.如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方). (1)求A、B两点的坐标;(2)设△OMN的面积为S,直线l运动时间为t秒(0≤t≤6),试求S 与t的函数表达式;(3)在题(2)的条件下,t为何值时,S的面积最大?最大面积是多少? 7.二次函数y=ax +bx+c的图象的一部分如图所示,已知它的顶点M在第二象限,且经过点A(1,0)和点B(0,1)。
(1)请判断实数a的取值范围,并说明理由;2xy1B1AO-1<a<0例2:有一根直尺的短边长2cm,长边长10cm,还有一块锐角为45°的直角三角形纸板,其中直角三角形纸板的斜边长为12cm.按图14—1的方式将直尺的短边DE放置在与直角三角形纸板的斜边AB上,且点D与点A重合.若直尺沿射线AB方向平行移动,如图14—2,设平移的长度为x(cm),直尺和三角形纸板的重叠部分(图中阴影部分)的面积为S cm 2).
(1)当x=0时,S=_____________;
当x = 10时,S =______________;
(2)当0<x≤4时,如图14—2,求S与x的函数关系式;
(3)当6<x<10时,求S与x的函数关系式;
(4)请你作出推测:当x为何值时,阴影部分的面积最大?并写出最大值.zxxkwA知识点1:用配方法或公式法求二次函数的最大(小)值
1.当-2≤x≤3时,二次函数y=x2-2x+3的最大值为_______,最小值为________.
知识点2:二次函数与图形面积问题
2.在一幅长60 cm,宽40 cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图(如图),如果要使整个挂图的面积是y cm2,设金色纸边的宽度为x cm,那么y与x之间的函数关系是( )
A.y=(60+2x)(40+2x)
B.y=(60+x)(40+x)
C.y=(60+2x)(40+x)
D.y=(60+x)(40+2x)112B 20m 第4题图 第5题图 C 800m2 6.如图,在△ABC中,∠B=90°,AB=8 cm,BC=6 cm,点P从点A开始沿AB向B点以2 cm/s的速度移动,点Q从点B开始沿BC向C点以1 cm/s的速度移动,如果P,Q分别同时出发,当△PBQ的面积为最大时,运动时间t为_______s.
7.小磊要制作一个三角形的钢架模型,在这个三角形中,长度为x(单位:cm)的边与这条边上的高之和为40 cm,这个三角形的面积S(单位:cm2)随x的变化而变化.
(1)S与x之间的函数关系式为____________________;
(2)当x=_______时,这个三角形面积S最大,最大面积是__________.220cm200cm28.如图,一个正方形纸板的边长为10 cm,将它割去一个正方形,留下四个全等的直角三角形(图中阴影部分).设AE=BF=CG=DH=x(cm),阴影部分的面积为y(cm2).
(1)求y关于x的函数解析式和自变量的取值范围;
(2)当x取何值时,阴影部分的面积达到最大,最大值为多少?解:(1)y=-2x2+20x(0<x<10) (2)配方得y=-2(x-5)2+50,
∴当x=5时,阴影面积最大,y最大=5012.5cm2 6cm (1)请直接写出S与x之间的函数关系式;(不要求写出自变量x的取值范围)
(2)当x是多少时,菱形风筝面积S最大?最大面积是多少?12.(2014·成都)在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x m.
(1)若花园的面积为192 m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15 m和6 m,
要将这棵树围在花园内(含边界,不考虑树的粗细),
求花园面积S的最大值.解:(1)由AB=x,得BC=28-x,根据题意, 得x(28-x)=192,解得x1=12,x2=16
(2)S=x(28-x)=-x2+28x=-(x-14)2+196,∵x≥6,
28-x≥15,∴6≤x≤13.∵a=-1<0,∴当6≤x≤13时,S随x的增大而增大,∴当x=13时,S有最大值195 m213.如图,等腰直角三角形ABC以2 cm/s的速度沿直线m匀速向正方形CDEF移动,直到AB与EF重合.设移动x s时,三角形与正方形重合部分的面积为y cm2.(1)当x=2,7时,y的值分别为多少?
(2)求从开始移动时到AB与EF重合时,
y与x的函数关系式,并求出x的取值范围.解:(1)当x=2时,y=8;当x=7时,y=421.理解问题;“二次函数应用” 的思路 回顾上一节“最大利润”和本节“最大面积”解决问题的过程,你能总结一下解决此类问题的基本思路吗?与同伴交流.2.分析问题中的变量和常量,以及它们之间的关系;3.用数学的方式表示出它们之间的关系;4.做数学求解;5.检验结果的合理性,拓展等.
同课章节目录
