福建省闽清县天儒中学(人教版)数学九年级上册课件:22-3实际问题与二次函数(共23张PPT)
文档属性
| 名称 | 福建省闽清县天儒中学(人教版)数学九年级上册课件:22-3实际问题与二次函数(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-06 15:10:11 | ||
图片预览



文档简介
课件23张PPT。实际问题与二次函数回忆抛物线的解析式有那几种形式?
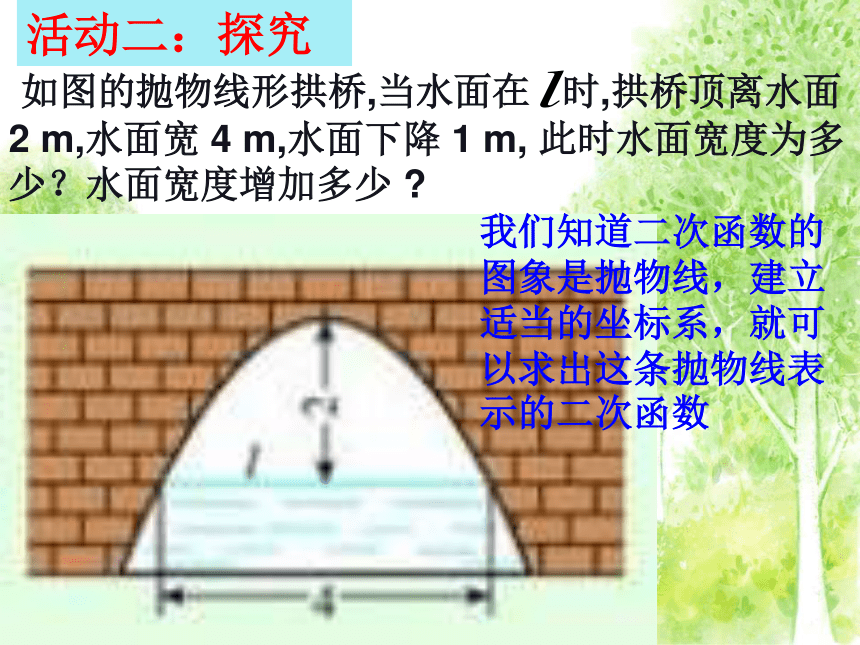
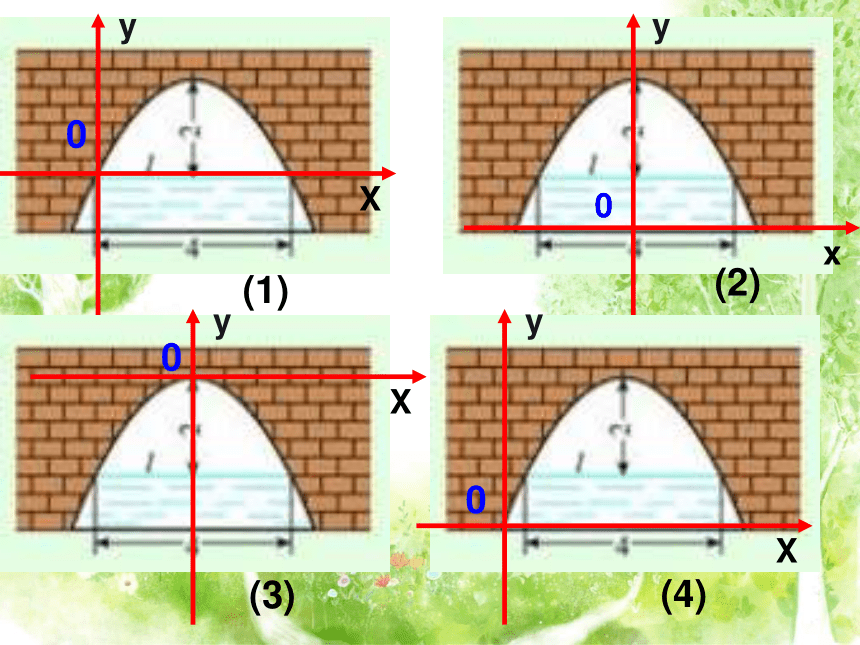
它们的图象大致是什么样的?(a≠0) 学科网 如图的抛物线形拱桥,当水面在 时,拱桥顶离水面 2 m,水面宽 4 m,水面下降 1 m, 此时水面宽度为多少?水面宽度增加多少 ?活动二:探究我们知道二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次函数 抛物线形拱桥,当水面在 时,拱顶离水面2m,水面宽度4m,水面下降1m,水面宽度为多少?水面宽度增加多少?0(2,-2)
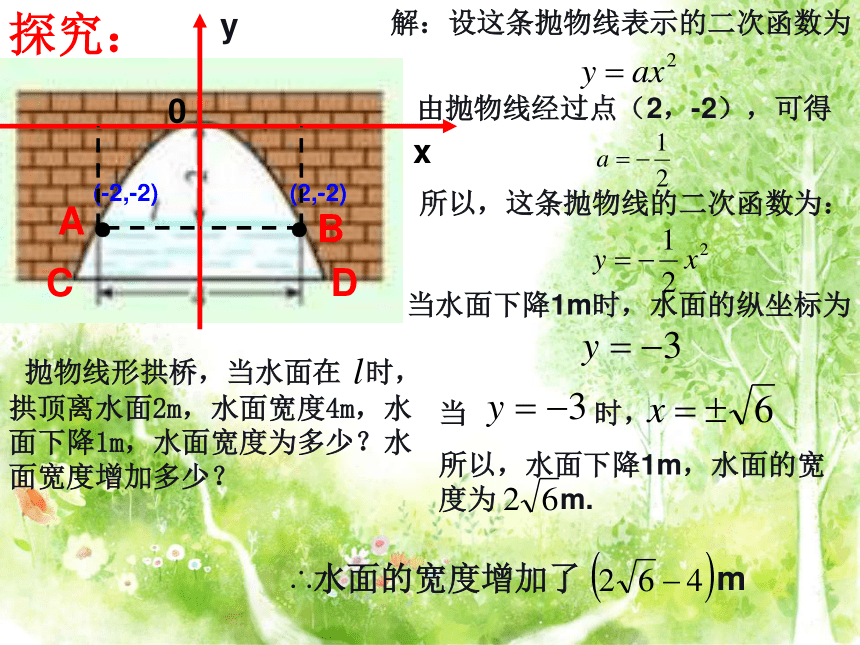
●(-2,-2)
●当 时,
所以,水面下降1m,水面的宽度为 m.∴水面的宽度增加了 m探究:解:设这条抛物线表示的二次函数为由抛物线经过点(2,-2),可得所以,这条抛物线的二次函数为:当水面下降1m时,水面的纵坐标为ABCD 抛物线形拱桥,当水面在 时,拱顶离水面2m,水面宽度4m,水面下降1m,水面宽度为多少?水面宽度增加多少?0(4, 0)
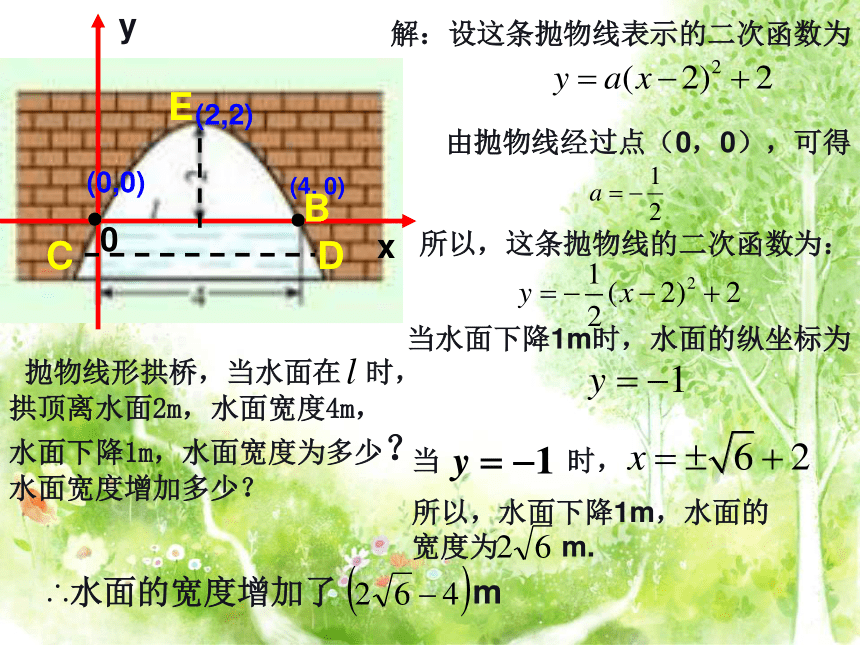
●(0,0)
●∴水面的宽度增加了 m(2,2)解:设这条抛物线表示的二次函数为由抛物线经过点(0,0),可得所以,这条抛物线的二次函数为:当 时,
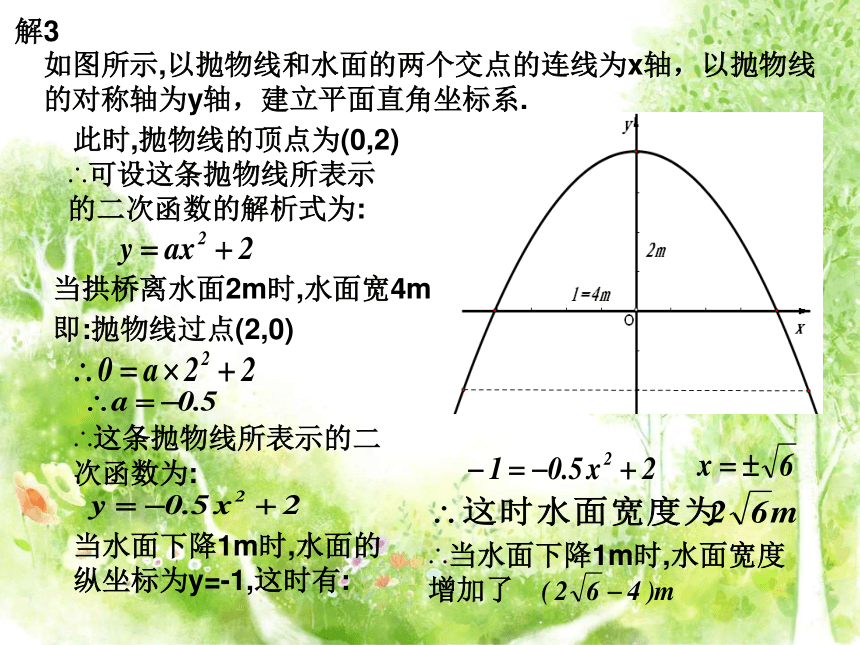
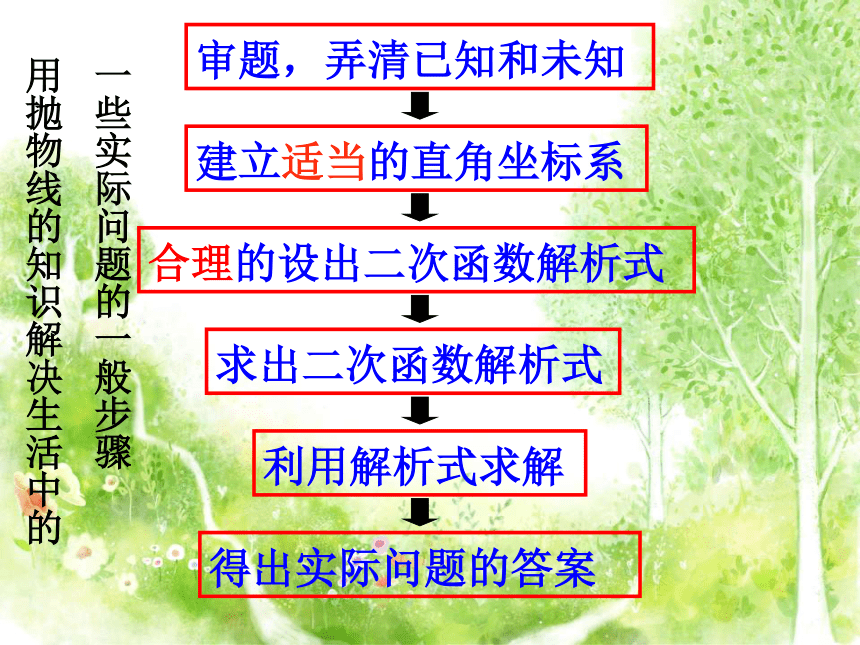
所以,水面下降1m,水面的宽度为 m.当水面下降1m时,水面的纵坐标为CDBE解3如图所示,以抛物线和水面的两个交点的连线为x轴,以抛物线的对称轴为y轴,建立平面直角坐标系.∴这条抛物线所表示的二次函数为:当水面下降1m时,水面的纵坐标为y=-1,这时有:∴当水面下降1m时,水面宽度增加了∴可设这条抛物线所表示的二次函数的解析式为:此时,抛物线的顶点为(0,2)0 000(1)(2)(3)(4)活动三:想一想 通过刚才的学习,你知道了用二次函数知识解决抛物线形建筑问题的一些经验吗?加 油建立适当的直角坐标系审题,弄清已知和未知合理的设出二次函数解析式 求出二次函数解析式 利用解析式求解得出实际问题的答案 :一些实际问题的一般步骤
用抛物线的知识解决生活中的练习:有一抛物线拱桥,已知水位在AB位置时,水面的宽度是 m,水位上升4 m就达到警戒线CD,这时水面宽是 米.若洪水到来时,水位以每小时0.5 m速度上升,求水过警戒线后几小时淹到拱桥顶端M处. 如图是某公园一圆形喷水池,水流在各方向沿形状相同的抛物线落下,如果喷头所在处A距地面1.25米,水流路线最高处B距地面2.25米,且距水池中心的水平距离为1米.试建立适当的坐标系,表示该抛物线的解析式为 ,如果不考虑其他因素,那么水池的半径至少要 米,才能使喷出的水流不致落到池外。 . y= -(x-1)2 +2.252.5当堂检测:1.25 例:某工厂大门是一抛物线形的水泥建筑物,大门底部宽AB=4m,顶部C离地面的高度为4.4m,现有载满货物的汽车欲通过大门,货物顶部距地面2.7m,装货宽度为2.4m.这辆汽车能否顺利通过大门?若能,请你通过计算加以说明;若不能,请简要说明理由.解:如图,以AB所在的直线为x轴,以AB的垂直平分线为y轴,建立平面直角坐标系.∵AB=4∴A(-2,0) B(2,0)∵OC=4.4∴C(0,4.4)设抛物线所表示的二次函数为∵抛物线过A(-2,0)∴抛物线所表示的二次函数为∴汽车能顺利经过大门.
一场篮球赛中,吴军跳起投篮,已知球出手时离地面高 米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米(如下图所示).
(1)已知篮球运行的路径为抛物线,求出此抛物线的函数解析式.0解:由题意可知,这段抛物线的顶点坐标是(4,4),设这条抛物线对应的函数解析式为:(0≤x≤10)03xy(0,3)吴军的出手高度为3m时
能将篮球投入篮圈03x(8,3)(7,3)(2) 在出手角度、力度及高度都不变的情况下,则吴军朝着篮球架再向前平移多少米后跳起投篮也能将篮球投入篮圈?y吴军朝着篮球架再向前平移1m
后跳起投篮也能将篮球投入篮圈如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线可以用
表示.(1)一辆货运卡车高4m,宽2m,它能通过该隧道吗?(2)如果该隧道内设双行道,那么这辆货运卡车是否可以通过?(1)卡车可以通过.提示:当x=±1时,y =3.75, 3.75+2>4.(2)卡车可以通过.提示:当x=±2时,y =3, 3+2>4. 练习某工厂大门是一抛物线型水泥建筑物,如图所示,大门地面宽AB=4m,顶部C离地面高度为4.4m。现有一辆满载货物的汽车欲通过大门,货物顶部距地面2.8m,装货宽度为2.4m。请判断这辆汽车能否顺利通过大门.
1.有一辆载有长方体体状集装箱的货车要想通过洞拱横截面为抛物线的隧道,如图1,已知沿底部宽AB为4m,高OC为3.2m;集装箱的宽与车的宽相同都是2.4m;集装箱顶部离地面2.1m。该车能通过隧道吗?请说明理由.练习如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.(1)设矩形的一边AB=x m那么AD边的程度如何表示?(2)设矩形的面积为y m2,当x取何值时,y的值最大?最大值是多少?当x=20时,y最大=3001.有一个抛物线型拱桥,拱顶O离水面高4米,
水面宽度AB=10米,现有一竹排运送一只货箱
欲从桥下经过,已知货箱的长10米,宽6米,
高2.55米(竹排与水面持平)问:货箱能否
顺利通过该桥?BACEFD2.周朗学过了抛物线的图象后,想测学校大
门的高度,如图所示,大门的地面宽度AB=18
米.他站在门内,在离门脚B点1米远的D处,
垂直地面立起一根1.7米长的木杆,其顶部恰好在抛物线门上C处,由此,他求出了大门的高度.你知道他求得的结果是什么?
●(-2,-2)
●当 时,
所以,水面下降1m,水面的宽度为 m.∴水面的宽度增加了 m探究:解:设这条抛物线表示的二次函数为由抛物线经过点(2,-2),可得所以,这条抛物线的二次函数为:当水面下降1m时,水面的纵坐标为ABCD 抛物线形拱桥,当水面在 时,拱顶离水面2m,水面宽度4m,水面下降1m,水面宽度为多少?水面宽度增加多少?0(4, 0)
●(0,0)
●∴水面的宽度增加了 m(2,2)解:设这条抛物线表示的二次函数为由抛物线经过点(0,0),可得所以,这条抛物线的二次函数为:当 时,
所以,水面下降1m,水面的宽度为 m.当水面下降1m时,水面的纵坐标为CDBE解3如图所示,以抛物线和水面的两个交点的连线为x轴,以抛物线的对称轴为y轴,建立平面直角坐标系.∴这条抛物线所表示的二次函数为:当水面下降1m时,水面的纵坐标为y=-1,这时有:∴当水面下降1m时,水面宽度增加了∴可设这条抛物线所表示的二次函数的解析式为:此时,抛物线的顶点为(0,2)0 000(1)(2)(3)(4)活动三:想一想 通过刚才的学习,你知道了用二次函数知识解决抛物线形建筑问题的一些经验吗?加 油建立适当的直角坐标系审题,弄清已知和未知合理的设出二次函数解析式 求出二次函数解析式 利用解析式求解得出实际问题的答案 :一些实际问题的一般步骤
用抛物线的知识解决生活中的练习:有一抛物线拱桥,已知水位在AB位置时,水面的宽度是 m,水位上升4 m就达到警戒线CD,这时水面宽是 米.若洪水到来时,水位以每小时0.5 m速度上升,求水过警戒线后几小时淹到拱桥顶端M处. 如图是某公园一圆形喷水池,水流在各方向沿形状相同的抛物线落下,如果喷头所在处A距地面1.25米,水流路线最高处B距地面2.25米,且距水池中心的水平距离为1米.试建立适当的坐标系,表示该抛物线的解析式为 ,如果不考虑其他因素,那么水池的半径至少要 米,才能使喷出的水流不致落到池外。 . y= -(x-1)2 +2.252.5当堂检测:1.25 例:某工厂大门是一抛物线形的水泥建筑物,大门底部宽AB=4m,顶部C离地面的高度为4.4m,现有载满货物的汽车欲通过大门,货物顶部距地面2.7m,装货宽度为2.4m.这辆汽车能否顺利通过大门?若能,请你通过计算加以说明;若不能,请简要说明理由.解:如图,以AB所在的直线为x轴,以AB的垂直平分线为y轴,建立平面直角坐标系.∵AB=4∴A(-2,0) B(2,0)∵OC=4.4∴C(0,4.4)设抛物线所表示的二次函数为∵抛物线过A(-2,0)∴抛物线所表示的二次函数为∴汽车能顺利经过大门.
一场篮球赛中,吴军跳起投篮,已知球出手时离地面高 米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米(如下图所示).
(1)已知篮球运行的路径为抛物线,求出此抛物线的函数解析式.0解:由题意可知,这段抛物线的顶点坐标是(4,4),设这条抛物线对应的函数解析式为:(0≤x≤10)03xy(0,3)吴军的出手高度为3m时
能将篮球投入篮圈03x(8,3)(7,3)(2) 在出手角度、力度及高度都不变的情况下,则吴军朝着篮球架再向前平移多少米后跳起投篮也能将篮球投入篮圈?y吴军朝着篮球架再向前平移1m
后跳起投篮也能将篮球投入篮圈如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线可以用
表示.(1)一辆货运卡车高4m,宽2m,它能通过该隧道吗?(2)如果该隧道内设双行道,那么这辆货运卡车是否可以通过?(1)卡车可以通过.提示:当x=±1时,y =3.75, 3.75+2>4.(2)卡车可以通过.提示:当x=±2时,y =3, 3+2>4. 练习某工厂大门是一抛物线型水泥建筑物,如图所示,大门地面宽AB=4m,顶部C离地面高度为4.4m。现有一辆满载货物的汽车欲通过大门,货物顶部距地面2.8m,装货宽度为2.4m。请判断这辆汽车能否顺利通过大门.
1.有一辆载有长方体体状集装箱的货车要想通过洞拱横截面为抛物线的隧道,如图1,已知沿底部宽AB为4m,高OC为3.2m;集装箱的宽与车的宽相同都是2.4m;集装箱顶部离地面2.1m。该车能通过隧道吗?请说明理由.练习如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.(1)设矩形的一边AB=x m那么AD边的程度如何表示?(2)设矩形的面积为y m2,当x取何值时,y的值最大?最大值是多少?当x=20时,y最大=3001.有一个抛物线型拱桥,拱顶O离水面高4米,
水面宽度AB=10米,现有一竹排运送一只货箱
欲从桥下经过,已知货箱的长10米,宽6米,
高2.55米(竹排与水面持平)问:货箱能否
顺利通过该桥?BACEFD2.周朗学过了抛物线的图象后,想测学校大
门的高度,如图所示,大门的地面宽度AB=18
米.他站在门内,在离门脚B点1米远的D处,
垂直地面立起一根1.7米长的木杆,其顶部恰好在抛物线门上C处,由此,他求出了大门的高度.你知道他求得的结果是什么?
同课章节目录
