福建省闽清县天儒中学(人教版)数学九年级上册课件:24.3 正多边形和圆(共44张PPT)
文档属性
| 名称 | 福建省闽清县天儒中学(人教版)数学九年级上册课件:24.3 正多边形和圆(共44张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-06 15:21:08 | ||
图片预览





文档简介
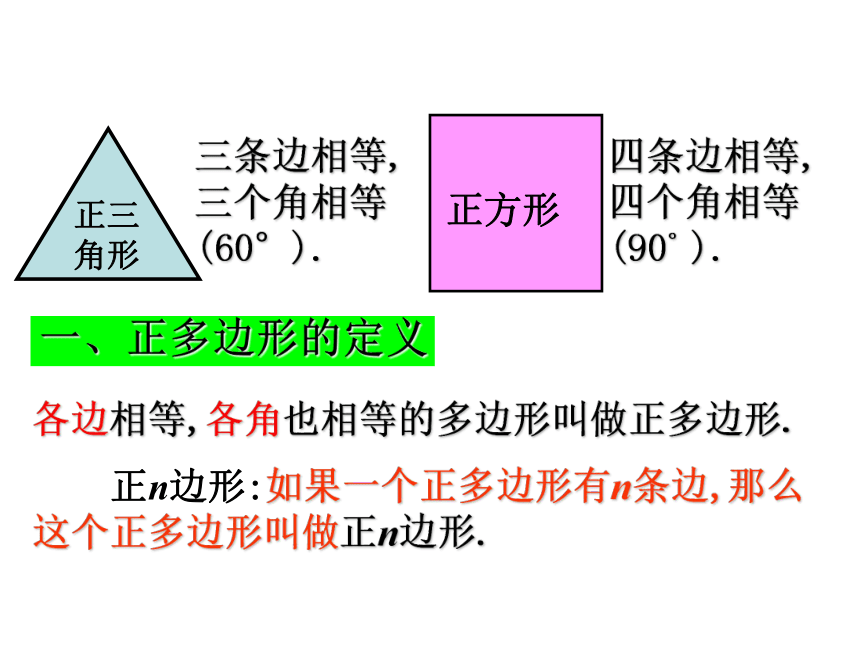
课件44张PPT。24.3 正多边形和圆观察下列图形它们有什么特点?正多边形的定义及性质各边相等,各角也相等的多边形叫做正多边形.
正n边形:如果一个正多边形有n条边,那么这个正多边形叫做正n边形.三条边相等,三个角相等(60°).四条边相等,四个角相等(90°).一、正多边形的定义想一想:
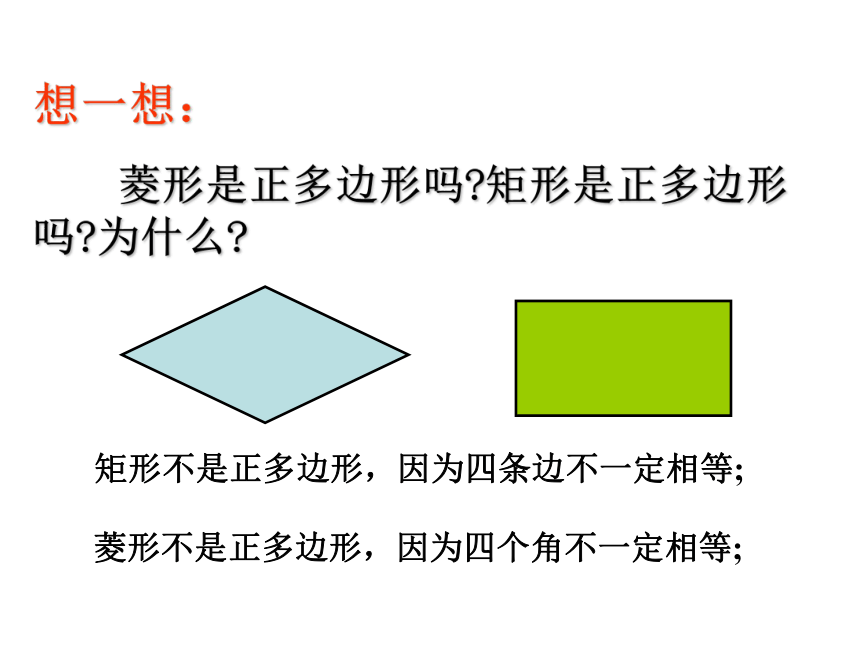
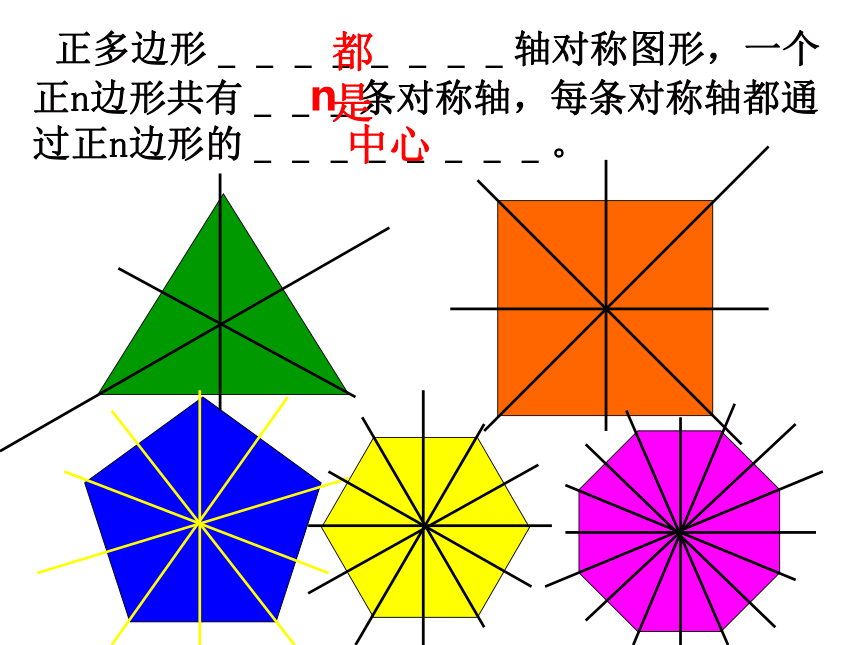
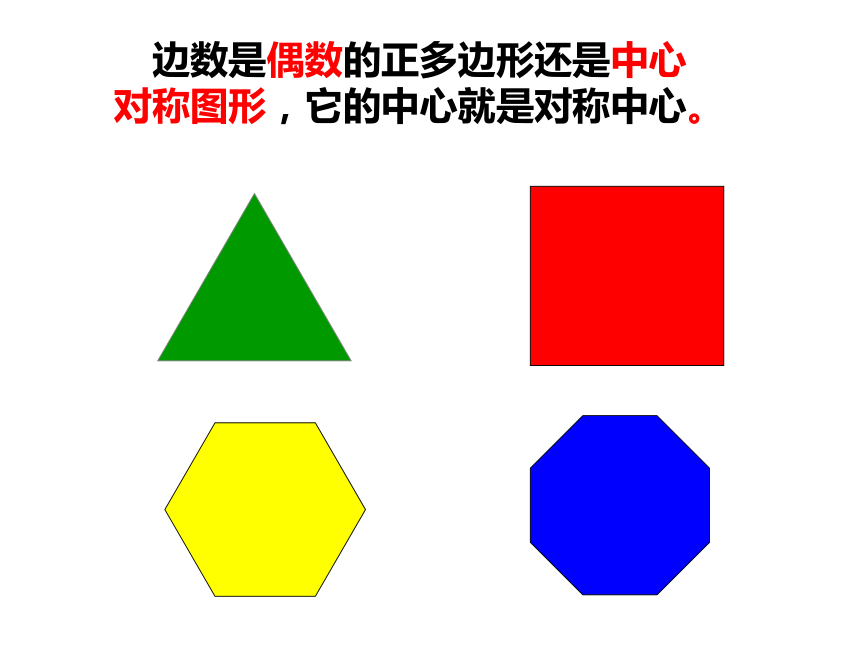
菱形是正多边形吗?矩形是正多边形吗?为什么?矩形不是正多边形,因为四条边不一定相等;菱形不是正多边形,因为四个角不一定相等; 正多边形________轴对称图形,一个正n边形共有___条对称轴,每条对称轴都通过正n边形的________。都是n中心 边数是偶数的正多边形还是中心
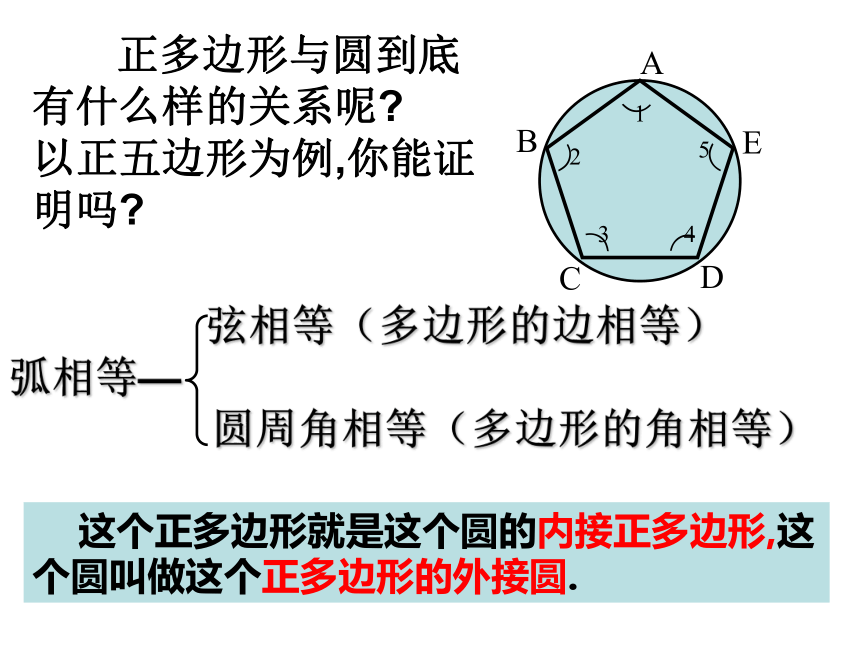
对称图形,它的中心就是对称中心。正多边形与圆的关系 正多边形与圆到底有什么样的关系呢?
以正五边形为例,你能证明吗? 弦相等(多边形的边相等)
弧相等—
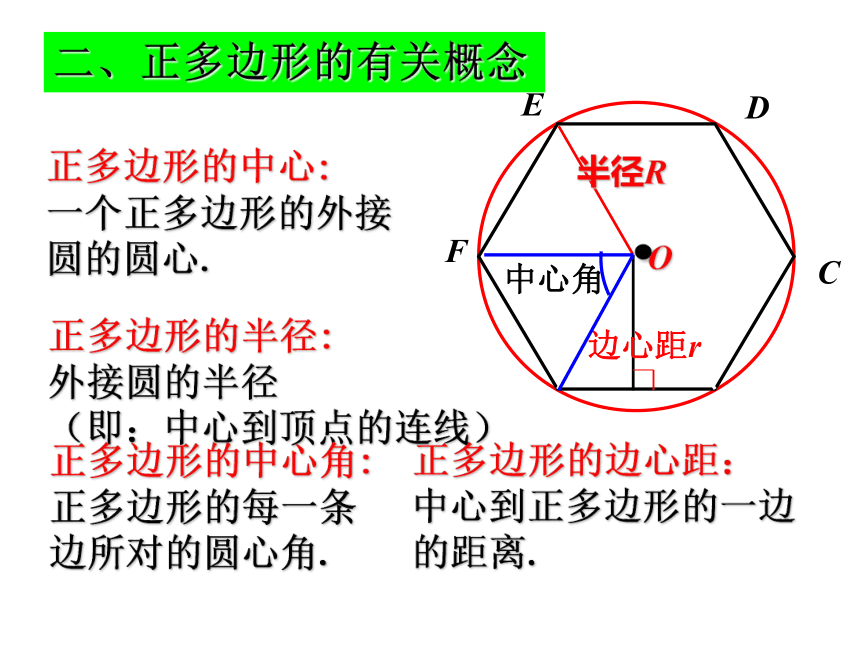
圆周角相等(多边形的角相等) 这个正多边形就是这个圆的内接正多边形,这个圆叫做这个正多边形的外接圆..O中心角半径R边心距r正多边形的中心:
一个正多边形的外接圆的圆心.正多边形的半径:
外接圆的半径
(即:中心到顶点的连线)正多边形的中心角:
正多边形的每一条
边所对的圆心角.正多边形的边心距:
中心到正多边形的一边
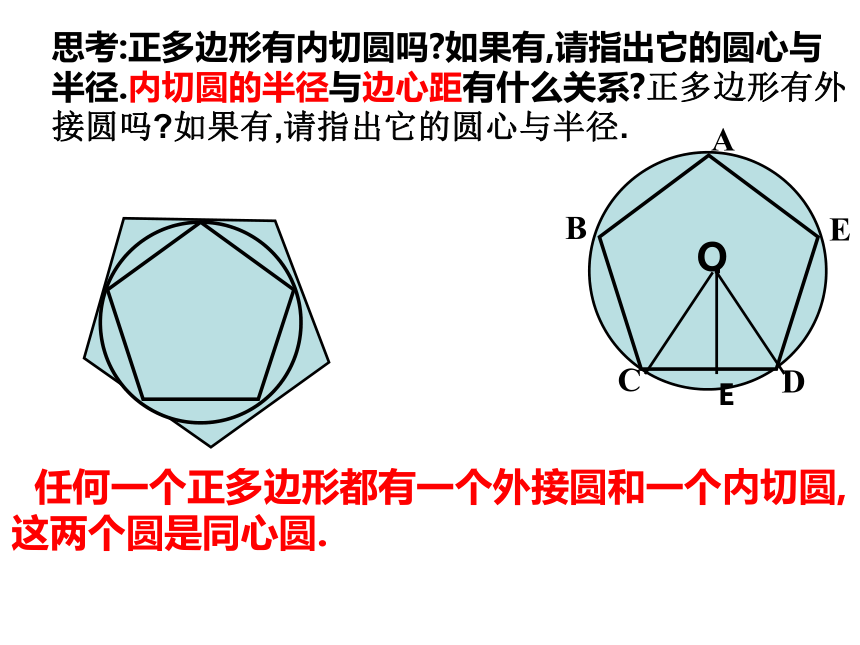
的距离.二、正多边形的有关概念·OE思考:正多边形有内切圆吗?如果有,请指出它的圆心与半径.内切圆的半径与边心距有什么关系?正多边形有外接圆吗?如果有,请指出它的圆心与半径. 任何一个正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆.2.OB叫等边△ABC的 ,它是正
△ABC的 圆的半径. 3.OD叫作等边△ABC的
它是等边△ABC的 圆的
半径.ABC .OD外接内切半径外接边心距内切4.正方形ABCD的外接圆圆心O叫做正方形
ABCD的 .5.正方形ABCD的内切圆的半径OE叫做正方形
ABCD的 .ABCD.OE中心边心距6.⊙O是正五边形ABCDE的外接圆,弦AB的弦心
距OF叫正五边形ABCDE的 ,它是正五
边形ABCDE的 圆的半径.7.∠AOB叫做正五边形
ABCDE的 角,
它的度数是 .DEABC.OF边心距内切中心72°8.图中正六边形ABCDEF的中心角是
它的度数是9.你发现正六边形
ABCDEF的半径
与边长具有什么
数量关系?
BA∠AOB60°相等判断题
①各边都相等的多边形是正多边形.( )
②一个圆有且只有一个内接正多边形.( )
2.证明题
求证:顺次连接正六边形各边
中点所得的多边形是正
六边形.ABCDEF××正多边形的有关计算.O中心角ABG边心距OG把△AOB分成2个全等的直角三角形 设正多边形的边长为a,半径为R,它的周长为 L=na.Ra 例 有一个亭子它的地基是半径为4m的正六边形,求地基的周长和面积(结果保留小数点后一位).例 有一个亭子,它的地基半径为4m的正六边形,求地基的周长和面积(精确到0.1m2).解: 如图由于ABCDEF是正六边形,所以它的中心角等于 ,△OBC是等边三角形,从而正六边形的边长等于它的半径.因此,亭子地基的周长l =4×6=24(m).在Rt△OPC中,OC=4, PC=利用勾股定理,可得边心距亭子地基的面积OABCDEFRPr活动33.分别求出半径为R的圆内接正三角形,正方形的边长,边心距和面积.解:作等边△ABC的BC边上的高AD,垂足为D连接OB,则OB=R在Rt△OBD中 ∠OBD=30°,边心距=OD=在Rt△ABD中 ∠BAD=30°,·ABCDO解:连接OB,OC 作OE⊥BC垂足为E,
∠OEB=90° ∠OBE= ∠ BOE=45°在Rt△OBE中为等腰直角三角形·ABCDOE利用圆画正多边形问题一:怎样画一个半径为2cm的正六边形呢? 例如,我们可以这样来画一个边长为2cm的正六边形.
第一种方法,如图,以2cm为半径作一个⊙O,用量角器画一个等于 的圆心角,它对着一段弧,然后在圆上依次截取与这
条弧相等的弧,就得到圆的6个等分点,顺次连接各分点,即可得出正六边形.·O利用这种方法可以画出任意的正n边形.第二种方法,如图,以2cm为半径作一个⊙O,由于正六边形的半径等于边长,所以在圆上依次截取等于2cm的弦,就可以将圆六等分,顺次连接各分点即可.·O 你能用以上方法画出正四边形、正五边吗?
你还有什么方法画正四边形、正六边形?D 你能尺规作出正八边形吗?
据此你还能作出哪些正多边形?·ABCDO只要作出已知⊙O的互相垂直的直径即得圆内接正方形,再过圆心作各边的垂线与⊙O相交,或作各中心角的角平分线与⊙O相交,即得圆接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形…… 你能尺规作出正六边形、正三角形、正十二边形吗?OABCEF·D 以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形……… ABCDEO如图:
已知点A、B、C、D、E是⊙O 的5等分点,画出⊙O的内接和外切正五边形
把圆分成n(n≥3)等份:
⑴依次连接各分点所得的多边形是这个圆的
内接正多边形;
⑵经过各分点作圆的切线,以相邻切线的交点
为顶点的多边形是这个圆的外切正多边形. 说说作正多边形的方法有哪些?归纳
(1)用量角器等分圆周作正n边形;
(2)用尺规作正方形及由此扩展作正八边形, 用尺规作正六边形及由此扩展作正12边形、正三角形. 小结:
怎样的多边形是正多边形?
各边相等,各角也相等的多边形叫做正多边形.正n边形与圆有密切的关系:1.把正n边形的边数无限增多,就接近于圆.
2.怎样由圆得到多边形呢? 1.各边_____,各角也_____的多边形是正多边形.
2.正多边形外接圆的圆心叫这个正多边形的_____,外接圆
的_____叫做这个正多边形的半径,正多边形的每一边所对的圆心角叫做正多边形的 ,中心到正多边形的一边的_____叫做正多边形 .
3.正多边形都是轴对称图形,但不一定是_____对称图形 相等相等中心半径中心角距离边心距中心知识点1:认识正多边形
1.一个正多边形的每个外角都等于36°,那么它是( )
A.正六边形 B.正八边形
C.正十边形 D.正十二边形
2.下列图形中,既是轴对称图形,又是中心对称图形的
有( )
①正三角形;②正方形;③正五边形;④正六边形;⑤线段;⑥圆;⑦菱形;⑧平行四边形.
A.3个 B.4个
C.5个 D.6个CC30° B C D D D (-4,0) 6 90° 72°
正n边形:如果一个正多边形有n条边,那么这个正多边形叫做正n边形.三条边相等,三个角相等(60°).四条边相等,四个角相等(90°).一、正多边形的定义想一想:
菱形是正多边形吗?矩形是正多边形吗?为什么?矩形不是正多边形,因为四条边不一定相等;菱形不是正多边形,因为四个角不一定相等; 正多边形________轴对称图形,一个正n边形共有___条对称轴,每条对称轴都通过正n边形的________。都是n中心 边数是偶数的正多边形还是中心
对称图形,它的中心就是对称中心。正多边形与圆的关系 正多边形与圆到底有什么样的关系呢?
以正五边形为例,你能证明吗? 弦相等(多边形的边相等)
弧相等—
圆周角相等(多边形的角相等) 这个正多边形就是这个圆的内接正多边形,这个圆叫做这个正多边形的外接圆..O中心角半径R边心距r正多边形的中心:
一个正多边形的外接圆的圆心.正多边形的半径:
外接圆的半径
(即:中心到顶点的连线)正多边形的中心角:
正多边形的每一条
边所对的圆心角.正多边形的边心距:
中心到正多边形的一边
的距离.二、正多边形的有关概念·OE思考:正多边形有内切圆吗?如果有,请指出它的圆心与半径.内切圆的半径与边心距有什么关系?正多边形有外接圆吗?如果有,请指出它的圆心与半径. 任何一个正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆.2.OB叫等边△ABC的 ,它是正
△ABC的 圆的半径. 3.OD叫作等边△ABC的
它是等边△ABC的 圆的
半径.ABC .OD外接内切半径外接边心距内切4.正方形ABCD的外接圆圆心O叫做正方形
ABCD的 .5.正方形ABCD的内切圆的半径OE叫做正方形
ABCD的 .ABCD.OE中心边心距6.⊙O是正五边形ABCDE的外接圆,弦AB的弦心
距OF叫正五边形ABCDE的 ,它是正五
边形ABCDE的 圆的半径.7.∠AOB叫做正五边形
ABCDE的 角,
它的度数是 .DEABC.OF边心距内切中心72°8.图中正六边形ABCDEF的中心角是
它的度数是9.你发现正六边形
ABCDEF的半径
与边长具有什么
数量关系?
BA∠AOB60°相等判断题
①各边都相等的多边形是正多边形.( )
②一个圆有且只有一个内接正多边形.( )
2.证明题
求证:顺次连接正六边形各边
中点所得的多边形是正
六边形.ABCDEF××正多边形的有关计算.O中心角ABG边心距OG把△AOB分成2个全等的直角三角形 设正多边形的边长为a,半径为R,它的周长为 L=na.Ra 例 有一个亭子它的地基是半径为4m的正六边形,求地基的周长和面积(结果保留小数点后一位).例 有一个亭子,它的地基半径为4m的正六边形,求地基的周长和面积(精确到0.1m2).解: 如图由于ABCDEF是正六边形,所以它的中心角等于 ,△OBC是等边三角形,从而正六边形的边长等于它的半径.因此,亭子地基的周长l =4×6=24(m).在Rt△OPC中,OC=4, PC=利用勾股定理,可得边心距亭子地基的面积OABCDEFRPr活动33.分别求出半径为R的圆内接正三角形,正方形的边长,边心距和面积.解:作等边△ABC的BC边上的高AD,垂足为D连接OB,则OB=R在Rt△OBD中 ∠OBD=30°,边心距=OD=在Rt△ABD中 ∠BAD=30°,·ABCDO解:连接OB,OC 作OE⊥BC垂足为E,
∠OEB=90° ∠OBE= ∠ BOE=45°在Rt△OBE中为等腰直角三角形·ABCDOE利用圆画正多边形问题一:怎样画一个半径为2cm的正六边形呢? 例如,我们可以这样来画一个边长为2cm的正六边形.
第一种方法,如图,以2cm为半径作一个⊙O,用量角器画一个等于 的圆心角,它对着一段弧,然后在圆上依次截取与这
条弧相等的弧,就得到圆的6个等分点,顺次连接各分点,即可得出正六边形.·O利用这种方法可以画出任意的正n边形.第二种方法,如图,以2cm为半径作一个⊙O,由于正六边形的半径等于边长,所以在圆上依次截取等于2cm的弦,就可以将圆六等分,顺次连接各分点即可.·O 你能用以上方法画出正四边形、正五边吗?
你还有什么方法画正四边形、正六边形?D 你能尺规作出正八边形吗?
据此你还能作出哪些正多边形?·ABCDO只要作出已知⊙O的互相垂直的直径即得圆内接正方形,再过圆心作各边的垂线与⊙O相交,或作各中心角的角平分线与⊙O相交,即得圆接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形…… 你能尺规作出正六边形、正三角形、正十二边形吗?OABCEF·D 以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形……… ABCDEO如图:
已知点A、B、C、D、E是⊙O 的5等分点,画出⊙O的内接和外切正五边形
把圆分成n(n≥3)等份:
⑴依次连接各分点所得的多边形是这个圆的
内接正多边形;
⑵经过各分点作圆的切线,以相邻切线的交点
为顶点的多边形是这个圆的外切正多边形. 说说作正多边形的方法有哪些?归纳
(1)用量角器等分圆周作正n边形;
(2)用尺规作正方形及由此扩展作正八边形, 用尺规作正六边形及由此扩展作正12边形、正三角形. 小结:
怎样的多边形是正多边形?
各边相等,各角也相等的多边形叫做正多边形.正n边形与圆有密切的关系:1.把正n边形的边数无限增多,就接近于圆.
2.怎样由圆得到多边形呢? 1.各边_____,各角也_____的多边形是正多边形.
2.正多边形外接圆的圆心叫这个正多边形的_____,外接圆
的_____叫做这个正多边形的半径,正多边形的每一边所对的圆心角叫做正多边形的 ,中心到正多边形的一边的_____叫做正多边形 .
3.正多边形都是轴对称图形,但不一定是_____对称图形 相等相等中心半径中心角距离边心距中心知识点1:认识正多边形
1.一个正多边形的每个外角都等于36°,那么它是( )
A.正六边形 B.正八边形
C.正十边形 D.正十二边形
2.下列图形中,既是轴对称图形,又是中心对称图形的
有( )
①正三角形;②正方形;③正五边形;④正六边形;⑤线段;⑥圆;⑦菱形;⑧平行四边形.
A.3个 B.4个
C.5个 D.6个CC30° B C D D D (-4,0) 6 90° 72°
同课章节目录
