福建省闽清县天儒中学(人教版)数学九年级上册课件:24-1-2垂直于弦的直径(共32张PPT)
文档属性
| 名称 | 福建省闽清县天儒中学(人教版)数学九年级上册课件:24-1-2垂直于弦的直径(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 232.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-06 15:14:22 | ||
图片预览






文档简介
课件32张PPT。垂直于弦的直径(1)24.1.2圆的垂径定理 这座桥建于隋开皇大业年间,由一名普通的石匠李春所建,距今已有1400多年的历史。在漫长的岁月中,虽然经历过无数次洪水冲击、风吹雨打、冰雪风霜的侵蚀和八次地震的考验,却仍然安然无恙、巍然挺立在洨河上。 这种设计,在建桥史上是一个创举,既减轻了流水对桥身的冲击力,使桥不容易被大水冲毁,又减轻了桥身的重量,节省了石料。直到19世纪中叶,才在欧洲国家出现,比赵州桥晚1200多年。赵州桥表现了劳动人民的智慧和才干,是我国宝贵的历史遗产。
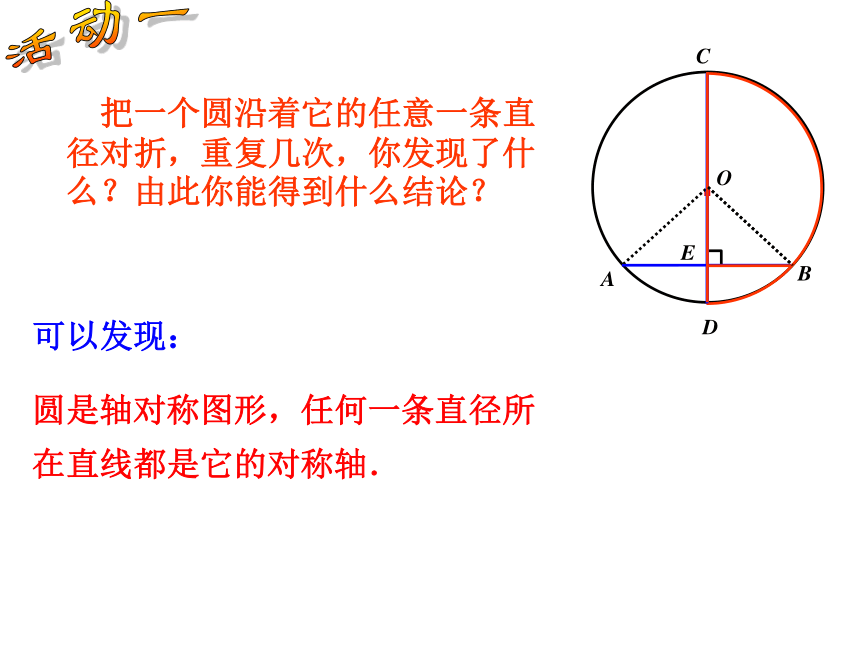
赵州桥的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵州桥主桥拱的半径吗? 赵州桥主桥拱的半径是多少? 问题情境圆的对称性圆是轴对称图形.圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.·OABCDE 把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?活动一可以发现:
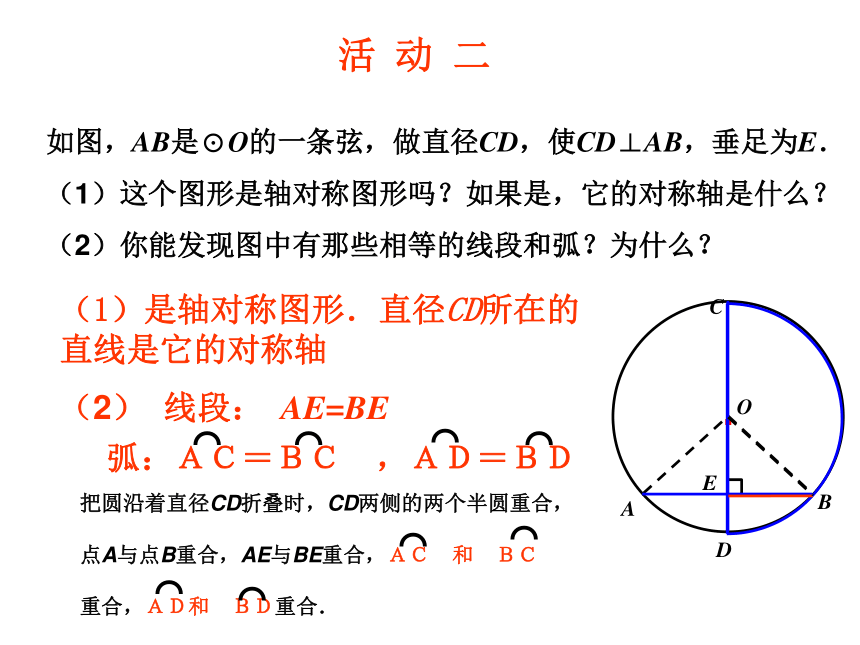
圆是轴对称图形,任何一条直径所在直线都是它的对称轴. 如图,AB是⊙O的一条弦,做直径CD,使CD⊥AB,垂足为E.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
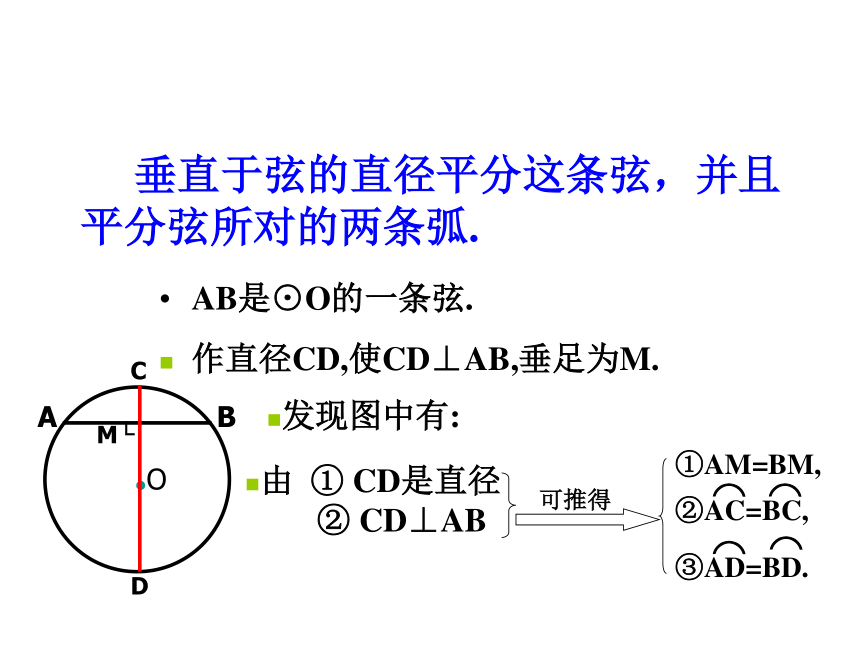
(2)你能发现图中有那些相等的线段和弧?为什么?·OABCDE活 动 二(1)是轴对称图形.直径CD所在的直线是它的对称轴(2) 线段: AE=BE①AM=BM,AB是⊙O的一条弦.作直径CD,使CD⊥AB,垂足为M.发现图中有:由 ① CD是直径② CD⊥AB 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.探究垂径定理结论的得出方法(1)利用折叠重合
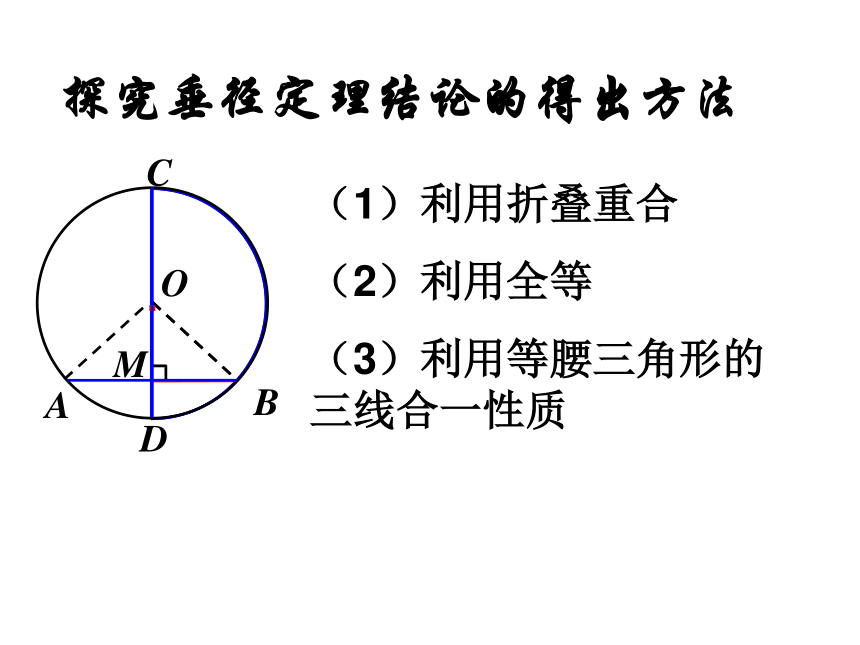
(2)利用全等
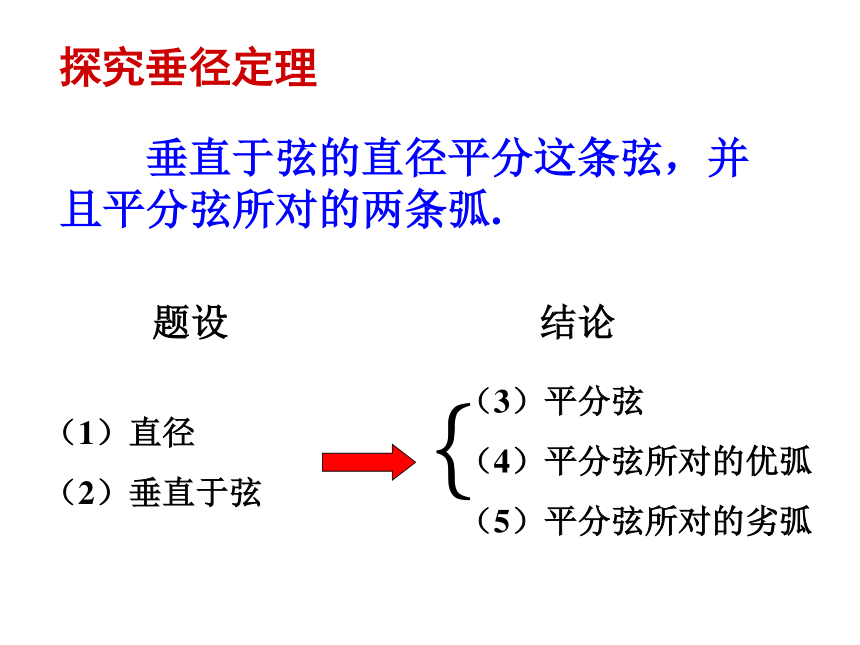
(3)利用等腰三角形的 三线合一性质·OAMBCD探究垂径定理 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.题设结论(1)直径
(2)垂直于弦{(3)平分弦
(4)平分弦所对的优弧
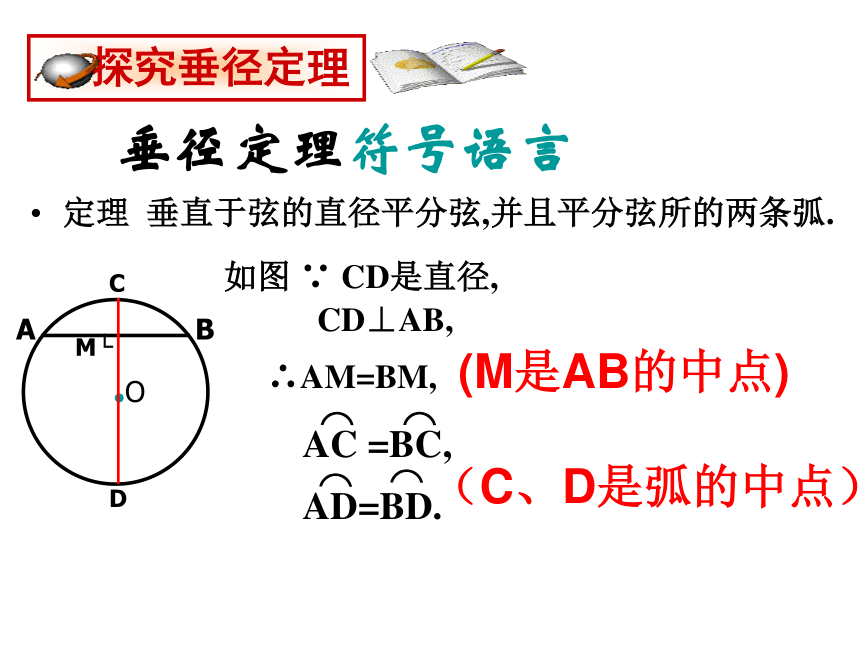
(5)平分弦所对的劣弧垂径定理符号语言定理 垂直于弦的直径平分弦,并且平分弦所的两条弧.CD⊥AB,如图 ∵ CD是直径,∴AM=BM, (M是AB的中点)
(C、D是弧的中点)·OABCDEzxxkw几何语言表达垂径定理:推论:判断下列说法的正误 ①平分弧的直径必平分弧所对的( ) ②平分弦的直线必垂直弦 ( )③垂直于弦的直径平分这条弦( ) ④平分弦的直径垂直于这条弦( ) ⑤弦的垂直平分线是圆的直径 ( )⑥平分弦所对的一条弧的直径必垂直这条弦( ) ⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧 ( )辨别是非解决求赵州桥拱半径的问题情境解决例2、赵州桥的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵州桥主桥拱的半径吗?解得:R≈27.9(m)解决求赵州桥拱半径的问题在Rt△OAD中,由勾股定理,得即 R2=18.72+(R-7.2)2∴赵州桥的主桥拱半径约为27.9m.OA2=AD2+OD2解:1.如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.·OABE练习解:答:⊙O的半径为5cm.在Rt △ AOE 中 zxxkw2.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形ADOE是正方形.证明:∴四边形ADOE为矩形,又 ∵AC=AB∴ AE=AD∴ 四边形ADOE为正方形. 某地有一座圆弧形拱桥圆心为O,桥下水面宽度为7.2 m ,过O 作OC ⊥ AB 于D, 交圆弧于C,CD=2.4m, 现有一艘宽3m,船舱顶部为方形并高出水面(AB)2m的货船要经过拱桥,此货船能否顺利通过这座拱桥?CNMAEHFBDO垂 径 定 理的基本图形的变身 垂直 直径 半径过圆心的直线如图,⊙O直径CD与弦AB(非直径)交于点M,添加一个条件:____________,就可得到点M是AB的中点.小试牛刀慧眼识金EEE在下列图形中,你能否利用垂径定理找到相等的线段或相等的圆弧⑸例1:一条排水管的截面如图所示。已知排水管的半径OB=10,水面宽AB=16。求截面圆心O到水面的距离。DC1088想一想:排水管中水最深多少?解:连结OA.
∵OM⊥AB,
∴
∵,OM=4,
∴AB=2AM=6(cm).变式1:如图所示,直径为10cm的 圆中,圆心到弦AB的距离4cm.
求弦AB的长.变式2、 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径。题后小结:1.作圆心到弦的距离和连半径是圆中常见的辅助线;2 .半径(r)、半弦、圆心到弦的距离(d)组成的直角三角形是研究与圆有关问题的主要思路,它们之间的关系:DC1088垂径定理的应用变式:如图,一条公路的转变处是一段圆弧(即图中弧CD,点O 是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD垂足为F,EF=90m.求这段弯路的半径。解:连接OC 例3、 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。EAC与BD相等证明:过点O作OE⊥AB于点E,则AE=BE,CE=DE,所以AE-CE=BE-DE,即AC=BD.
变式 :如图,已知AB为 ⊙O 的直径,AC为弦,OD⊥AC,交AC于点D,BC=6cm,求OD的长。
ACBDO新建 (6).doc 如图,过已知P为⊙O内的一点,你能用三角尺画⊙O 的一条弦AB,使点P恰为AB的中点吗?说明你的理由。BC就是所要求的弦
适度拓展1.本节课主要内容:
(1)圆的轴对称性;(2)垂径定理.2.垂径定理的应用:
计算和证明.颗粒归仓3、小结解题的主要方法: (1) 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。 (2)半径(r)、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路,它们之间的关系:
赵州桥的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵州桥主桥拱的半径吗? 赵州桥主桥拱的半径是多少? 问题情境圆的对称性圆是轴对称图形.圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.·OABCDE 把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?活动一可以发现:
圆是轴对称图形,任何一条直径所在直线都是它的对称轴. 如图,AB是⊙O的一条弦,做直径CD,使CD⊥AB,垂足为E.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
(2)你能发现图中有那些相等的线段和弧?为什么?·OABCDE活 动 二(1)是轴对称图形.直径CD所在的直线是它的对称轴(2) 线段: AE=BE①AM=BM,AB是⊙O的一条弦.作直径CD,使CD⊥AB,垂足为M.发现图中有:由 ① CD是直径② CD⊥AB 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.探究垂径定理结论的得出方法(1)利用折叠重合
(2)利用全等
(3)利用等腰三角形的 三线合一性质·OAMBCD探究垂径定理 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.题设结论(1)直径
(2)垂直于弦{(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧垂径定理符号语言定理 垂直于弦的直径平分弦,并且平分弦所的两条弧.CD⊥AB,如图 ∵ CD是直径,∴AM=BM, (M是AB的中点)
(C、D是弧的中点)·OABCDEzxxkw几何语言表达垂径定理:推论:判断下列说法的正误 ①平分弧的直径必平分弧所对的( ) ②平分弦的直线必垂直弦 ( )③垂直于弦的直径平分这条弦( ) ④平分弦的直径垂直于这条弦( ) ⑤弦的垂直平分线是圆的直径 ( )⑥平分弦所对的一条弧的直径必垂直这条弦( ) ⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧 ( )辨别是非解决求赵州桥拱半径的问题情境解决例2、赵州桥的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵州桥主桥拱的半径吗?解得:R≈27.9(m)解决求赵州桥拱半径的问题在Rt△OAD中,由勾股定理,得即 R2=18.72+(R-7.2)2∴赵州桥的主桥拱半径约为27.9m.OA2=AD2+OD2解:1.如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.·OABE练习解:答:⊙O的半径为5cm.在Rt △ AOE 中 zxxkw2.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形ADOE是正方形.证明:∴四边形ADOE为矩形,又 ∵AC=AB∴ AE=AD∴ 四边形ADOE为正方形. 某地有一座圆弧形拱桥圆心为O,桥下水面宽度为7.2 m ,过O 作OC ⊥ AB 于D, 交圆弧于C,CD=2.4m, 现有一艘宽3m,船舱顶部为方形并高出水面(AB)2m的货船要经过拱桥,此货船能否顺利通过这座拱桥?CNMAEHFBDO垂 径 定 理的基本图形的变身 垂直 直径 半径过圆心的直线如图,⊙O直径CD与弦AB(非直径)交于点M,添加一个条件:____________,就可得到点M是AB的中点.小试牛刀慧眼识金EEE在下列图形中,你能否利用垂径定理找到相等的线段或相等的圆弧⑸例1:一条排水管的截面如图所示。已知排水管的半径OB=10,水面宽AB=16。求截面圆心O到水面的距离。DC1088想一想:排水管中水最深多少?解:连结OA.
∵OM⊥AB,
∴
∵,OM=4,
∴AB=2AM=6(cm).变式1:如图所示,直径为10cm的 圆中,圆心到弦AB的距离4cm.
求弦AB的长.变式2、 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径。题后小结:1.作圆心到弦的距离和连半径是圆中常见的辅助线;2 .半径(r)、半弦、圆心到弦的距离(d)组成的直角三角形是研究与圆有关问题的主要思路,它们之间的关系:DC1088垂径定理的应用变式:如图,一条公路的转变处是一段圆弧(即图中弧CD,点O 是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD垂足为F,EF=90m.求这段弯路的半径。解:连接OC 例3、 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。EAC与BD相等证明:过点O作OE⊥AB于点E,则AE=BE,CE=DE,所以AE-CE=BE-DE,即AC=BD.
变式 :如图,已知AB为 ⊙O 的直径,AC为弦,OD⊥AC,交AC于点D,BC=6cm,求OD的长。
ACBDO新建 (6).doc 如图,过已知P为⊙O内的一点,你能用三角尺画⊙O 的一条弦AB,使点P恰为AB的中点吗?说明你的理由。BC就是所要求的弦
适度拓展1.本节课主要内容:
(1)圆的轴对称性;(2)垂径定理.2.垂径定理的应用:
计算和证明.颗粒归仓3、小结解题的主要方法: (1) 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。 (2)半径(r)、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路,它们之间的关系:
同课章节目录
