福建省闽清县天儒中学(人教版)数学九年级上册课件:24.1.4圆周角(共20张PPT)
文档属性
| 名称 | 福建省闽清县天儒中学(人教版)数学九年级上册课件:24.1.4圆周角(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 153.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-06 14:00:00 | ||
图片预览





文档简介
课件20张PPT。24.1.4 圆周角(2)一条弧所对的圆周角等它所对的圆心角的一半.顶点在圆上,两边与圆相交的角,叫圆周角.圆周角的概念圆周角定理 推论:
1.同弧或等弧所对的圆周角相等;
2.半圆(或直径)所对的圆周角是直角;
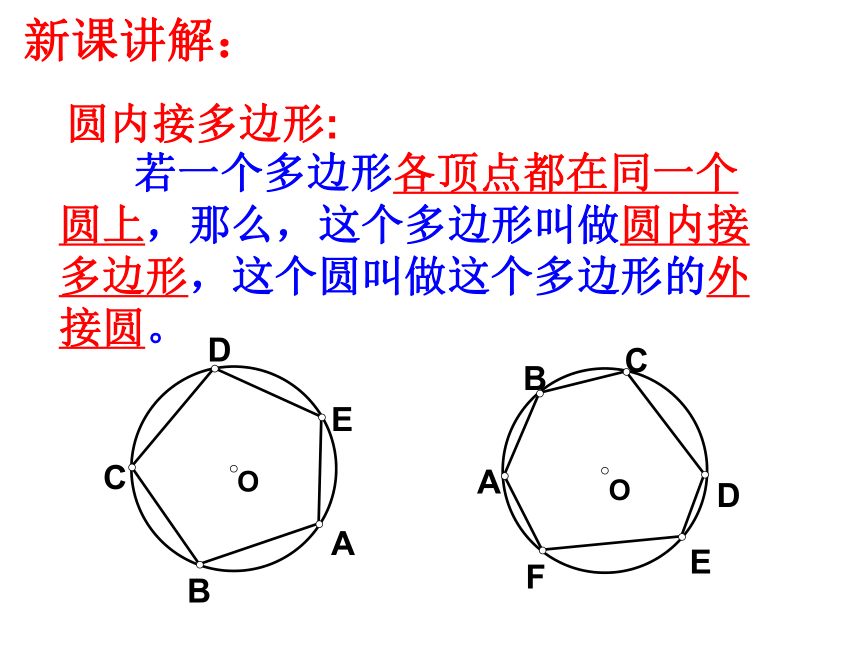
90°的圆周角所对的弦是圆的直径.复习巩固 新课讲解: 若一个多边形各顶点都在同一个圆上,那么,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆。OACDEB圆内接多边形:如图:
四边形ABCD为⊙O的内接四边形;
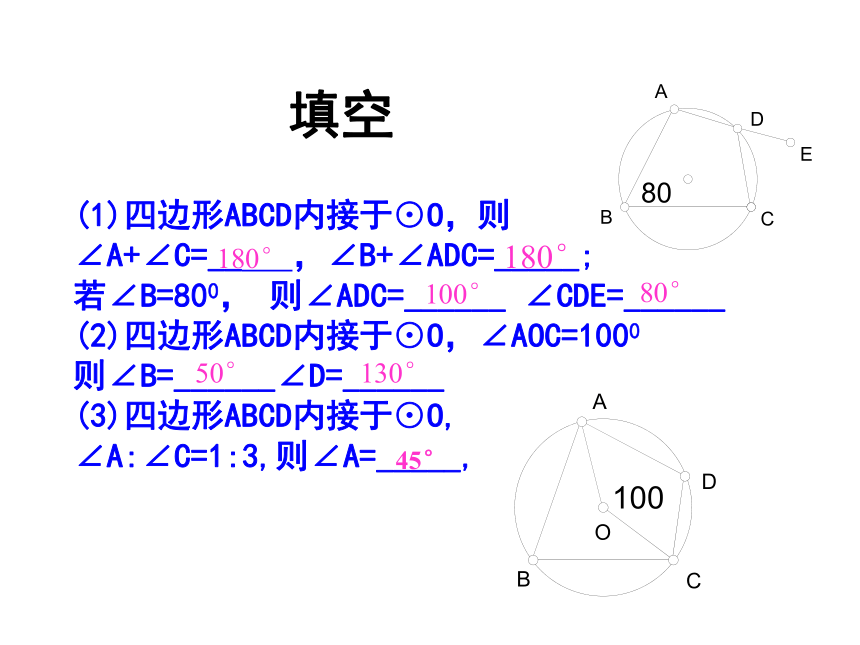
⊙O为四边形ABCD的外接圆。 CODBA如图:圆内接四边形ABCD中,∵ 弧BCD和弧BAD所对的圆心角的和是周角∴∠A+∠C=180° 同理∠B+∠D=180°定理:圆的内接四边形的对角互补。归纳: (1)四边形ABCD内接于⊙O,则 ∠A+∠C=__ ,∠B+∠ADC=_____; 若∠B=800, 则∠ADC=______ ∠CDE=______ (2)四边形ABCD内接于⊙O,∠AOC=1000 则∠B=______∠D=______ (3)四边形ABCD内接于⊙O, ∠A:∠C=1:3,则∠A=_____, 180° 180° 100° 80°
?
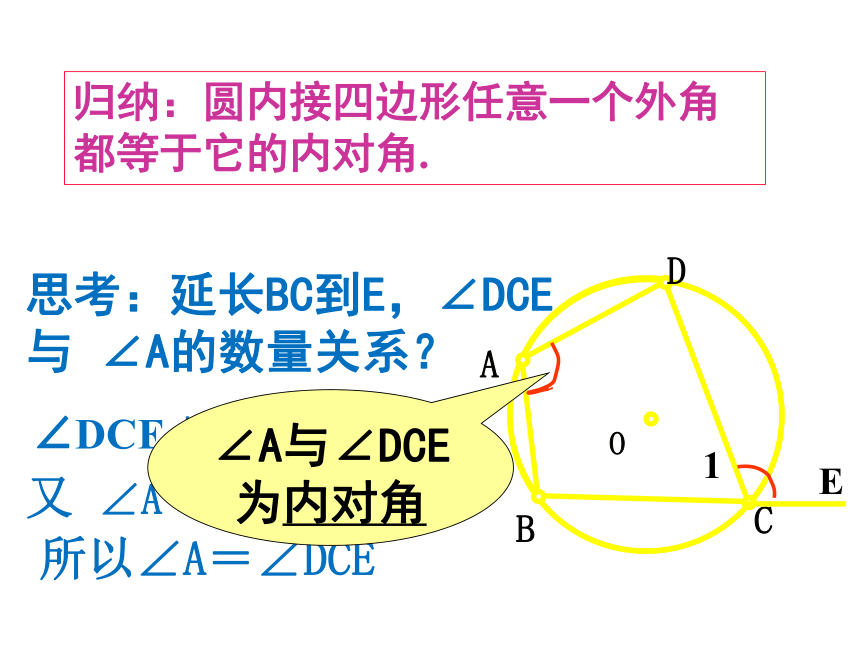
50° 130° 45° 填空思考:延长BC到E,∠DCE与 ∠A的数量关系?180°所以∠A=∠DCE又 ∠A +∠1= 180°∠DCE+∠1 =归纳:圆内接四边形任意一个外角都等于它的内对角.∠A与∠DCE为内对角4.若ABCD为圆内接四边形,则下列哪个选项可能成立( )(A)∠A∶∠B∶∠C∶∠D = 1∶2∶3∶4 (B)∠A∶∠B∶∠C∶∠D = 2∶1∶3∶4 (C)∠A∶∠B∶∠C∶∠D = 3∶2∶1∶4 (D)∠A∶∠B∶∠C∶∠D = 4∶3∶2∶1B2018年11月23日星期五
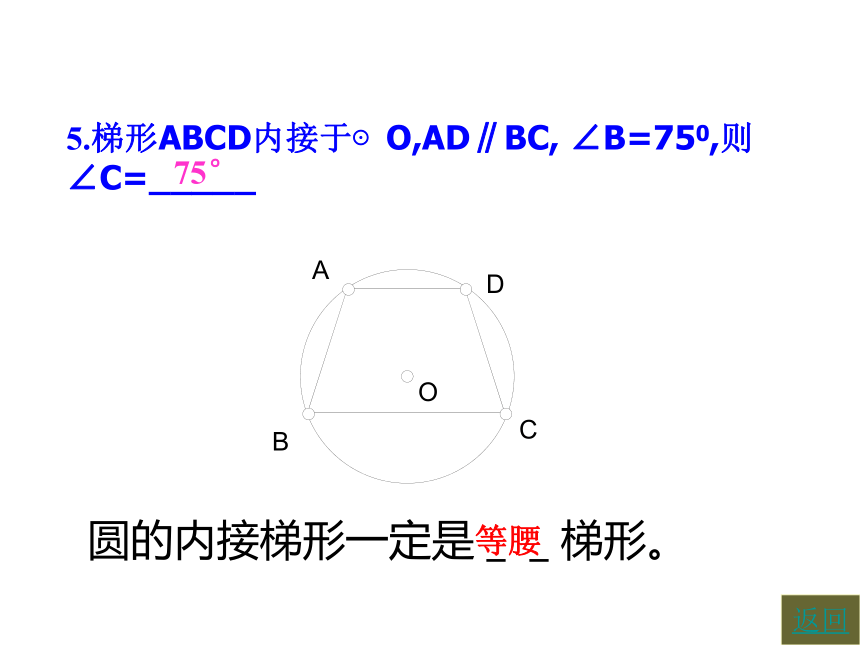
5.梯形ABCD内接于⊙O,AD∥BC, ∠B=750,则∠C=_____
75°返回圆的内接梯形一定是__梯形。等腰例1已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
(1)BD与CD的大小有什么关系?为什么?
(2)求证:⌒ ⌒BD=DE 连结AD.∵AB是圆的直径,点D在圆上,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴BD=CD,
AD平分顶角∠BAC,即∠BAD=∠CAD,∴ ⌒ ⌒BD= DE(同圆或等圆中相等的圆周角所对弧相等)解:BD=CD.理由是:1、在⊙O中,∠CBD=30°,∠BDC=20°,求∠A。解:∵∠CBD=300,∠BDC=200
∴∠C=1800-∠CBD-∠BDC=1300
∴∠A=1800-∠C=500(圆内接四边形对角互补)巩固:变式:已知∠OAB等于40度,求∠C的度数. D2、如图,在⊙O中,AB为直径,CB=CF,
弦CG⊥AB,交AB于D,交BF于E。
求证:BE=EC))BE=EC∠EBC=∠ECBAB为直径CG⊥AB4、判断
(1)等弧所对的圆周角相等;( )
(2)相等的弦所对的圆周角也相等;( )
(3)900的角所对的弦是直径;( )
(4)同弦所对的圆周角相等。( )√×××证明:连结AB 例1: 如图4,⊙O1和⊙O2都经过A、B两点, 经过点A的直线CD
与⊙O1相交于点C,与⊙O2相交于点D,经过点B的直线EF与⊙O1
相交于点E,与⊙O2相交于点F。
求证:CE∥DF ∵ABEC是⊙O1的内接四边形 ∴∠1+∠E =1800 又∵ADFB是⊙O2的内接四边形 ∴∠1=∠F. ∴∠E+∠F=1800 ∴CE∥DF 1反思与拓展 证明两条直线平行的方法很多,但常用的还是通过证明同位角相等、内错角相等、同旁内角互补等方法。刚才我们通过同旁内角互补证明了CE ∥ DF,想一想还能否通过同位角相等或者内错角相等证明结果? 1)延长EF,是否有∠E=∠BAD= ∠1 ?
2) 延长DF, 能否证明∠E=∠2=∠3? 变式1:如图,⊙O1和⊙O2都经过A、B两点,过A点的直线CD与⊙O1交于点C,与⊙O2交于点D,过B点的直线EF与⊙O1交于点E,与⊙O2交于点F。
EDCFAB猜想:CE∥DF仍然成立吗?
O1O2变式2:如图,⊙O1和⊙O2有两个公共点A﹑B,过A﹑B两点的直线分别交⊙O1于C 、E,交⊙O2于D 、F,且
CD∥EF。
CEABDFO1O2 求证:CE=DF
思维拓展:1、圆内接平行四边形一定是 形。
2、圆内接梯形一定是 形。3、圆内接菱形一定是 形。矩等腰梯正方弧、弦与圆心角的
关系定理:1、在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.2、在同圆或等圆中,相等的弧所对的圆心角相等, 所对的弦也相等。3、在同圆或等圆中,相等的弦所对的圆心角相等,所对的弧也相等.弧、弦与圆周角的关系定理:1、在同圆或等圆中,相等的圆周角所对的弧相等,所对的弦也相等.2、在同圆或等圆中,相等的弧所对的圆周角相等, 所对的弦也相等。3、在同圆或等圆中,相等的弦所对的圆周角相等或互补!圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
1.同弧或等弧所对的圆周角相等;
2.半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是圆的直径.复习巩固 新课讲解: 若一个多边形各顶点都在同一个圆上,那么,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆。OACDEB圆内接多边形:如图:
四边形ABCD为⊙O的内接四边形;
⊙O为四边形ABCD的外接圆。 CODBA如图:圆内接四边形ABCD中,∵ 弧BCD和弧BAD所对的圆心角的和是周角∴∠A+∠C=180° 同理∠B+∠D=180°定理:圆的内接四边形的对角互补。归纳: (1)四边形ABCD内接于⊙O,则 ∠A+∠C=__ ,∠B+∠ADC=_____; 若∠B=800, 则∠ADC=______ ∠CDE=______ (2)四边形ABCD内接于⊙O,∠AOC=1000 则∠B=______∠D=______ (3)四边形ABCD内接于⊙O, ∠A:∠C=1:3,则∠A=_____, 180° 180° 100° 80°
?
50° 130° 45° 填空思考:延长BC到E,∠DCE与 ∠A的数量关系?180°所以∠A=∠DCE又 ∠A +∠1= 180°∠DCE+∠1 =归纳:圆内接四边形任意一个外角都等于它的内对角.∠A与∠DCE为内对角4.若ABCD为圆内接四边形,则下列哪个选项可能成立( )(A)∠A∶∠B∶∠C∶∠D = 1∶2∶3∶4 (B)∠A∶∠B∶∠C∶∠D = 2∶1∶3∶4 (C)∠A∶∠B∶∠C∶∠D = 3∶2∶1∶4 (D)∠A∶∠B∶∠C∶∠D = 4∶3∶2∶1B2018年11月23日星期五
5.梯形ABCD内接于⊙O,AD∥BC, ∠B=750,则∠C=_____
75°返回圆的内接梯形一定是__梯形。等腰例1已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
(1)BD与CD的大小有什么关系?为什么?
(2)求证:⌒ ⌒BD=DE 连结AD.∵AB是圆的直径,点D在圆上,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴BD=CD,
AD平分顶角∠BAC,即∠BAD=∠CAD,∴ ⌒ ⌒BD= DE(同圆或等圆中相等的圆周角所对弧相等)解:BD=CD.理由是:1、在⊙O中,∠CBD=30°,∠BDC=20°,求∠A。解:∵∠CBD=300,∠BDC=200
∴∠C=1800-∠CBD-∠BDC=1300
∴∠A=1800-∠C=500(圆内接四边形对角互补)巩固:变式:已知∠OAB等于40度,求∠C的度数. D2、如图,在⊙O中,AB为直径,CB=CF,
弦CG⊥AB,交AB于D,交BF于E。
求证:BE=EC))BE=EC∠EBC=∠ECBAB为直径CG⊥AB4、判断
(1)等弧所对的圆周角相等;( )
(2)相等的弦所对的圆周角也相等;( )
(3)900的角所对的弦是直径;( )
(4)同弦所对的圆周角相等。( )√×××证明:连结AB 例1: 如图4,⊙O1和⊙O2都经过A、B两点, 经过点A的直线CD
与⊙O1相交于点C,与⊙O2相交于点D,经过点B的直线EF与⊙O1
相交于点E,与⊙O2相交于点F。
求证:CE∥DF ∵ABEC是⊙O1的内接四边形 ∴∠1+∠E =1800 又∵ADFB是⊙O2的内接四边形 ∴∠1=∠F. ∴∠E+∠F=1800 ∴CE∥DF 1反思与拓展 证明两条直线平行的方法很多,但常用的还是通过证明同位角相等、内错角相等、同旁内角互补等方法。刚才我们通过同旁内角互补证明了CE ∥ DF,想一想还能否通过同位角相等或者内错角相等证明结果? 1)延长EF,是否有∠E=∠BAD= ∠1 ?
2) 延长DF, 能否证明∠E=∠2=∠3? 变式1:如图,⊙O1和⊙O2都经过A、B两点,过A点的直线CD与⊙O1交于点C,与⊙O2交于点D,过B点的直线EF与⊙O1交于点E,与⊙O2交于点F。
EDCFAB猜想:CE∥DF仍然成立吗?
O1O2变式2:如图,⊙O1和⊙O2有两个公共点A﹑B,过A﹑B两点的直线分别交⊙O1于C 、E,交⊙O2于D 、F,且
CD∥EF。
CEABDFO1O2 求证:CE=DF
思维拓展:1、圆内接平行四边形一定是 形。
2、圆内接梯形一定是 形。3、圆内接菱形一定是 形。矩等腰梯正方弧、弦与圆心角的
关系定理:1、在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.2、在同圆或等圆中,相等的弧所对的圆心角相等, 所对的弦也相等。3、在同圆或等圆中,相等的弦所对的圆心角相等,所对的弧也相等.弧、弦与圆周角的关系定理:1、在同圆或等圆中,相等的圆周角所对的弧相等,所对的弦也相等.2、在同圆或等圆中,相等的弧所对的圆周角相等, 所对的弦也相等。3、在同圆或等圆中,相等的弦所对的圆周角相等或互补!圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
同课章节目录
