福建省闽清县天儒中学(人教版)数学九年级上册课件:24.1.4圆周角(共41张PPT)
文档属性
| 名称 | 福建省闽清县天儒中学(人教版)数学九年级上册课件:24.1.4圆周角(共41张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 330.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-06 13:50:13 | ||
图片预览


文档简介
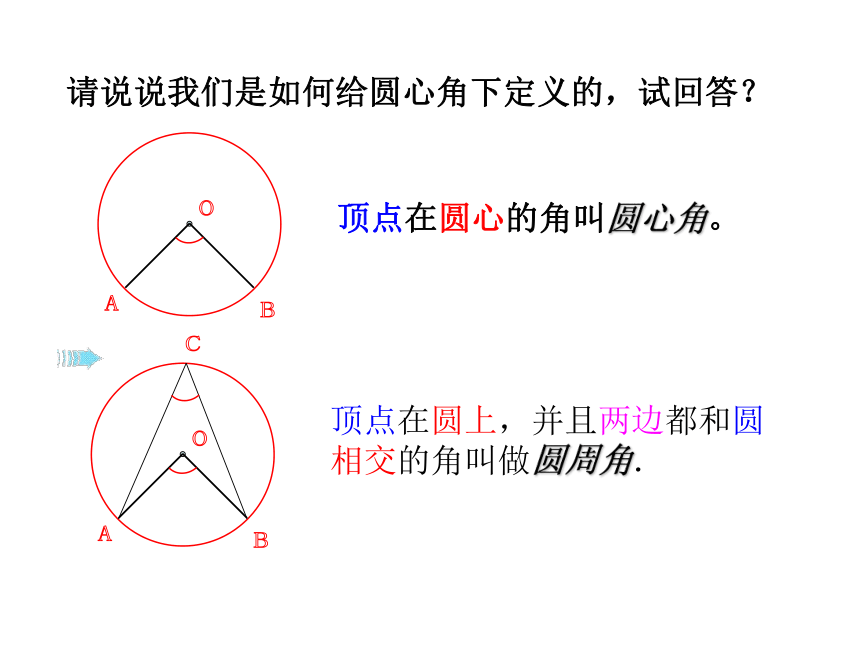
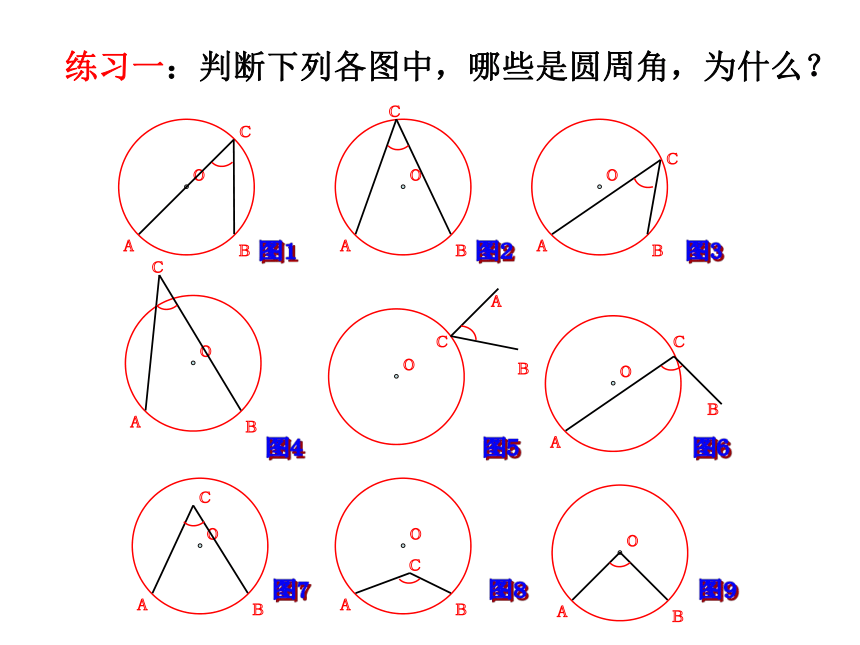
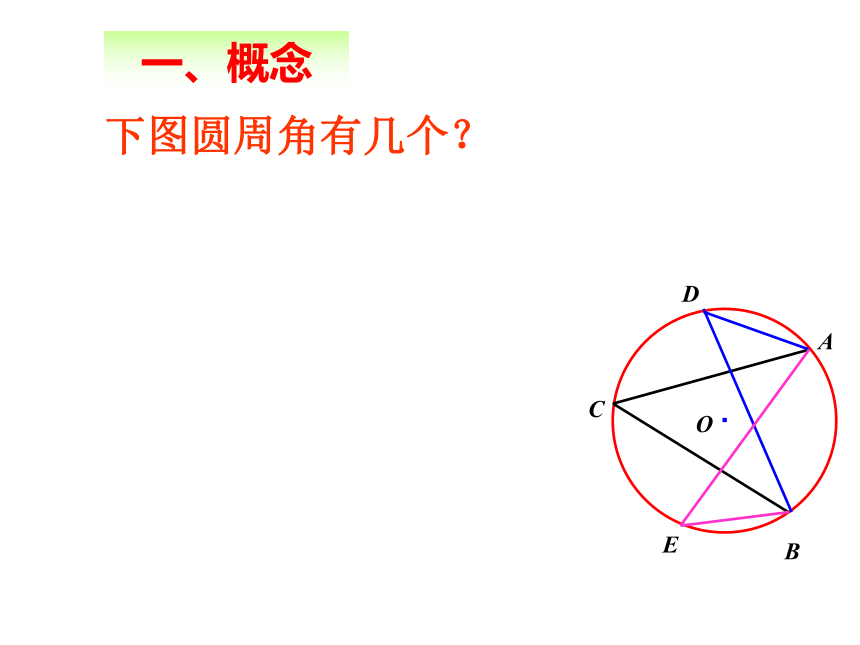
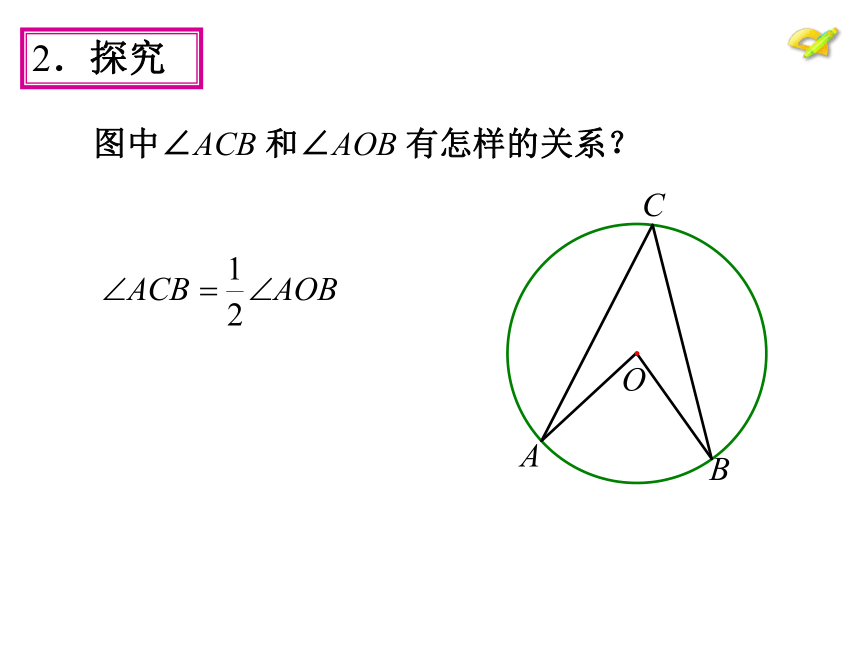
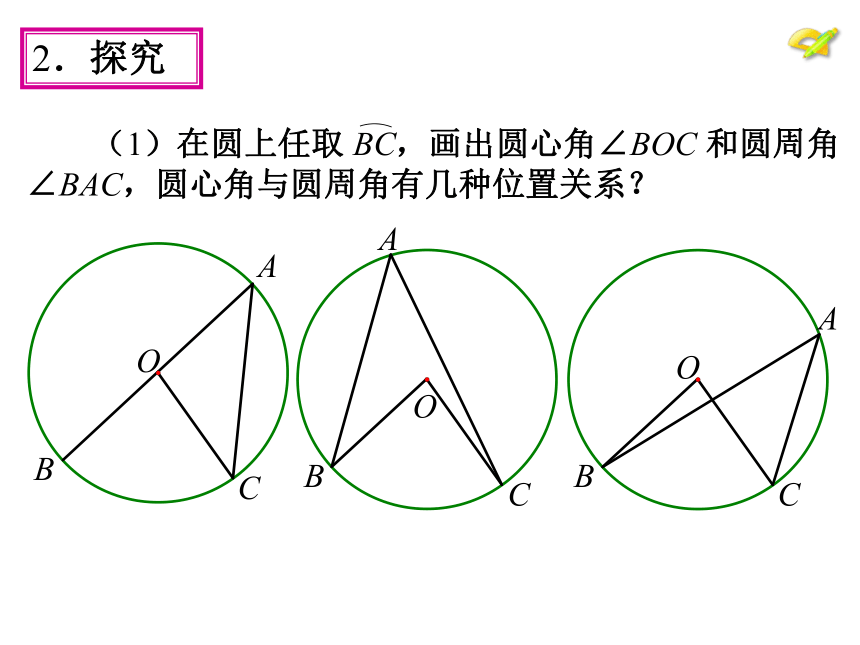
课件41张PPT。24.1.4 圆周角学科网学.科.网请说说我们是如何给圆心角下定义的,试回答?顶点在圆心的角叫圆心角。顶点在圆上,并且两边都和圆相交的角叫做圆周角. 练习一:判断下列各图中,哪些是圆周角,为什么? oABoABoABoABoABoABoABoABCCCCCCCC图1图2图3图4图5图6图7图8图9下图圆周角有几个?·ABCO一、概念 图中∠ACB 和∠AOB 有怎样的关系?2.探究2.探究为了进一步探究上面的发现,如图,在⊙O上任取一个圆周角∠BAC,将圆对折,使折痕经过圆心O和∠BAC的顶点A.由于点A的位置的取法可能不同,所以折痕可能会:
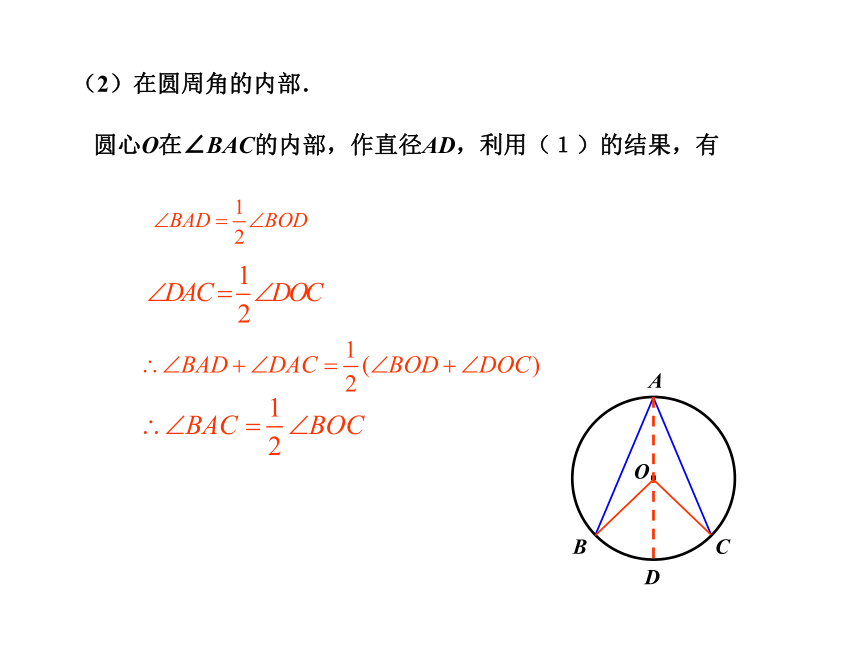
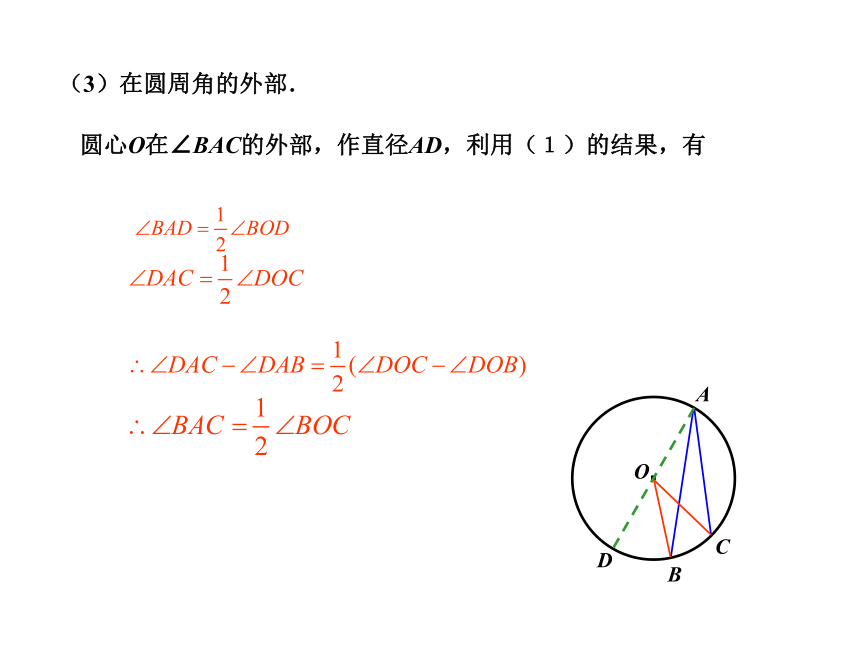
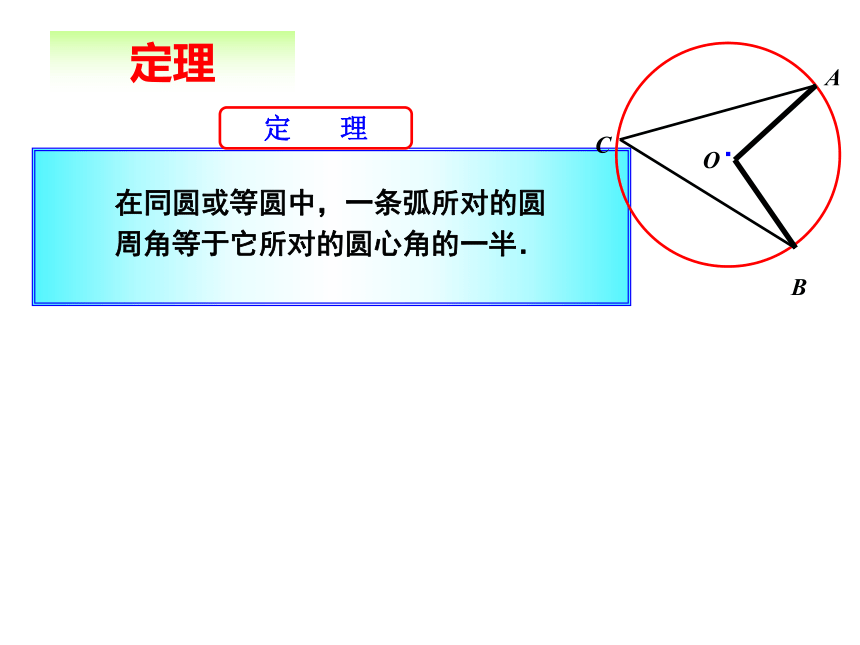
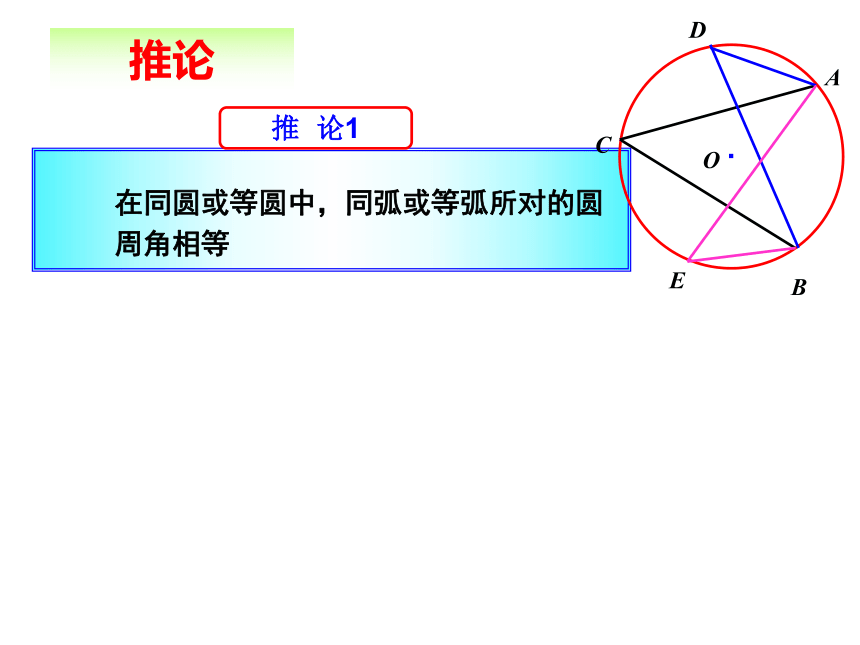
(1)在圆周角的一条边上.·COAB同弧所对的圆周角与圆心角的关系即 ∵OA=OC ,∴∠A=∠C .又 ∠BOC=∠A+∠C,∴∠BOC=2∠A.(2)在圆周角的内部.圆心O在∠BAC的内部,作直径AD,利用(1)的结果,有·COABD(3)在圆周角的外部.圆心O在∠BAC的外部,作直径AD,利用(1)的结果,有·COABD定理·ABCO推论·ABCO·ABC1OC2C3推论1.如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?ABCD12345678∠1 = ∠4∠5 = ∠8∠2 = ∠7∠3 = ∠6方法点拔:由同弧来找相等的圆周角练习:600BP例题 1、在⊙O中,∠CBD=30° ,∠BDC=20°,求∠A解法一: 1、在⊙O中,∠CBD=30° ,∠BDC=20°,求∠A解法二: 2、如图,在⊙O中,AB为直径,CB = CF,
弦CG⊥AB,交AB于D,交BF于E
求证:BE=EC
例题⌒⌒在同圆或等圆中,如果两个圆周角相等,它们所对的弧一定相等吗?为什么?结论:在同圆或等圆中,如果两个圆周角相等,它们所对弧一定相等.因为,在同圆或等圆中,如果圆周角相等,那么它所对的圆心角也相等,因此它所对的弧也相等. 如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm, ?ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长.5.应用解:连接 OD,AD,BD, ∵ AB 是⊙O 的直径,
∴ ?ACB=?ADB=90°.
在 Rt△ABC 中,
BC= = =8(cm) 如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm, ?ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长.5.应用 1.如图,以⊙O的半径OA为直径作⊙O1,⊙O的弦AD交⊙O1于C,则OC与AD的位置关系是_____, OC与BD的位置关系是_____,若AC=2cm,则AD=__cm。垂直平行4随堂练习学科网 3.如图,∠A=50°,∠ABC=60 °,BD是
⊙O的直径,则∠AEB等于( )
A.70° B.110°
C.90° D.120° 2.如图AB,AC为⊙O的两条弦,
延长CA到D,使AD=AB,若∠ADB=300.
则∠BOC=________。EB1200随堂练习zxxkw3. 求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆.)·ABCO已知:△ABC ,CO为AB边上的中线,求证: △ABC 为直角三角形.证明:CO= AB,以AB为直径作⊙O.∵AO=BO, ∴AO=BO=CO.∴点C在⊙O上.又∵AB为⊙O的直径,∴∠ACB= ×180°= 90°.且CO= AB.∴ △ABC 为直角三角形.5、已知⊙O中弦AB的长等于半径,
求弦AB所对的圆心角和圆周角的度数。 圆心角为60度圆周角为 30 度或 150 度。例2 在足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻,当甲带球冲到A点时,乙已跟随冲到B点(如图2).此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好?分析 在真正的足球比赛中情况会很复杂,这里仅用数学方法从两点的静止状态加以考虑,如果两个点到球门的距离相差不大,要确定较好的射门位置,关键看这两个点分别对球门MN的张角大小,当张角较小时,则球容易被对方守门员拦截.怎样比较A、B两点对MN张角的大小呢?解 考虑过M、N以及A、B中的任一点作一圆,这里不妨作出⊙BMN,显然,A点在⊙BMN外,设MA交圆于C,则
∠MAN<∠MCN,而∠MCN=∠MBN,
所以∠MAN<∠MBN.
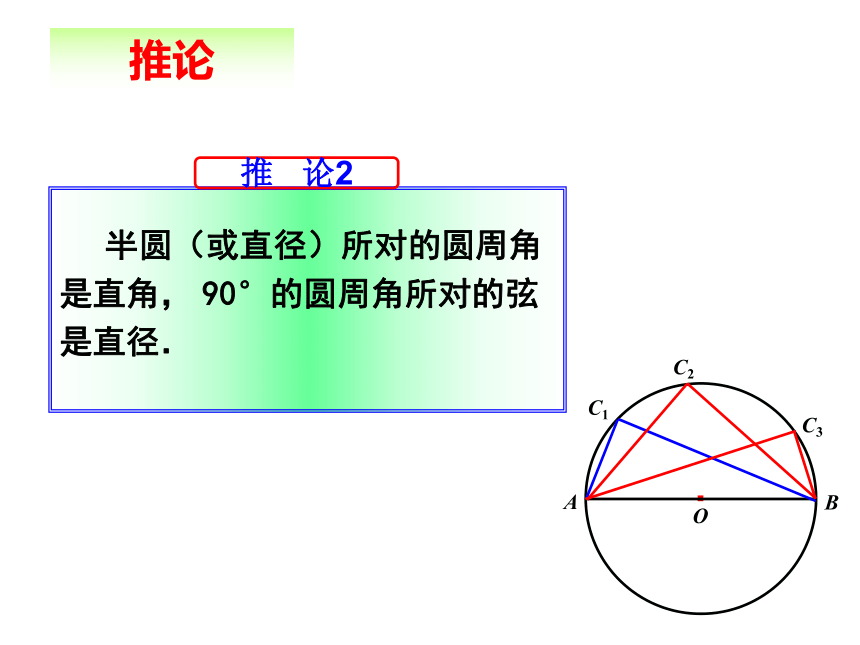
因此,甲应将球回传给乙,让乙射门.1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.3.在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等。2.半圆或直径所对的圆周角都相等,都等于90°
90°的圆周角所对的弦是圆的直径小结:zxxkwzxxkw 1.如图,以⊙O的半径OA为直径作⊙O1,⊙O的弦AD交⊙O1于C,则OC与AD的位置关系是_____, OC与BD的位置关系是_____,若AC=2cm,则AD=__cm。垂直平行4随堂练习学科网 3.如图,∠A=50°,∠ABC=60 °,BD是
⊙O的直径,则∠AEB等于( )
A.70° B.110°
C.90° D.120° 2.如图AB,AC为⊙O的两条弦,
延长CA到D,使AD=AB,若∠ADB=300.
则∠BOC=________。EB1200随堂练习zxxkw分析:同一条弧所对的圆周角有很多,圆周角的位置灵活多变,可以把注意力放在圆周角所对的弧上.4. 如图,AB是⊙O的直径, C 和D是圆上的两点,若∠ABD=40°,求∠BCD的度数.40°随堂练习例2. 如图,AB为⊙O的一条固定直径,自上半圆上一点C,作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在半圆(不含A,B两点)上移动时,问:点P的位置是否变化?例题讲解分析 连结AO,CO,由勾股定理不难得到△ABD为等腰直角三角形,则∠AOC==90°,又OA=OC,AC长度已知,则可以求出半径和直径. 更一般的情况要用正弦定理来求.OCBAD5. 如图,A,B,C三点在⊙O上,AD⊥BC于D,且AC=5,DC=3,AB= ,求⊙O的直径.随堂练习 1如图,⊙O中,弦DC、AB的延长线相交于点P,如果∠AOD=1200,∠BDC=250,那么
∠P= .350走进中考 2如图,在⊙O中,∠AOB的度数为m.C是∠ACB上
一点,D、E是AB弧上不同的两点
(不与A,B两点重合),则∠D+∠E的度数为( )
A.m B. C. D.走进中考 B 如果一个多边形的所有顶点都在同一个圆上,
这个多边形就叫做圆内接多边形,这个圆叫做这个
多边形的外接圆. 如图,四边形ABCD是⊙O
的内接四边形, ⊙O是四边形
ABCD的外接圆。思考:∠A+∠C=? 能用圆周角定理证明你的结论吗? 圆内接四边形的对角互补。 6.如图,⊙O中,∠A0B = 80o,则∠ACB=____.140oD随堂练习 7.求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆.)·ABCO求证: △ABC 为直角三角形.证明:以AB为直径作⊙O,∵AO=BO, ∴AO=BO=CO.∴点C在⊙O上.又∵AB为直径,∴∠ACB= 90°.∴ △ABC 为直角三角形.CO= AB,随堂练习 1.船在航行过程中,船长常常通过测定角度来测定是否会遇到暗礁,如图表示灯塔,暗礁分布在经过A、B两点的一个圆形区域内,C表示一个危险临界点,∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁。
1)当船与两个灯塔的夹角α大于“危险角”时,船位于哪个区域?为什么?
2)当船与两个灯塔的夹角α
小于“危险角”时,船位于哪个
区域?为什么?
拓展提高 2.如图,在足球比赛中,甲、乙两名队员互相配合向对方球门MN进攻,当甲带球冲到A点时,乙已跟随冲到B点,从数学角度看,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好?
BANMC拓展提高 提示:从数学角度看,甲、乙谁射门好,关键是比较∠MAN与∠MBN的大小,角度越大,射门的机会越好。
zxxkwzxxkw 2.如图,在足球比赛中,甲、乙两名队员互相配合向对方球门MN进攻,当甲带球冲到A点时,乙已跟随冲到B点,从数学角度看,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好?
拓展提高 提示:从数学角度看,甲、乙谁射门好,关键是比较∠MAN与∠MBN的大小,角度越大,射门的机会越好。
3.如图,点P是圆上的一个动点,弦AB= ,PC是∠APB的平分线,∠BAC=300.
(1)当∠PAC等于多少度时四边形PACB有最大面积?最大面积是多少?
(2)当∠PAC等于多少度时四边形PACB是梯形?拓展提高 P1P2P3如图,你能设法确定一个圆形纸片的圆心吗?你有多少种方法?与同学交流一下.DOOO·方法一方法二方法三方法四AB合作交流
(1)在圆周角的一条边上.·COAB同弧所对的圆周角与圆心角的关系即 ∵OA=OC ,∴∠A=∠C .又 ∠BOC=∠A+∠C,∴∠BOC=2∠A.(2)在圆周角的内部.圆心O在∠BAC的内部,作直径AD,利用(1)的结果,有·COABD(3)在圆周角的外部.圆心O在∠BAC的外部,作直径AD,利用(1)的结果,有·COABD定理·ABCO推论·ABCO·ABC1OC2C3推论1.如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?ABCD12345678∠1 = ∠4∠5 = ∠8∠2 = ∠7∠3 = ∠6方法点拔:由同弧来找相等的圆周角练习:600BP例题 1、在⊙O中,∠CBD=30° ,∠BDC=20°,求∠A解法一: 1、在⊙O中,∠CBD=30° ,∠BDC=20°,求∠A解法二: 2、如图,在⊙O中,AB为直径,CB = CF,
弦CG⊥AB,交AB于D,交BF于E
求证:BE=EC
例题⌒⌒在同圆或等圆中,如果两个圆周角相等,它们所对的弧一定相等吗?为什么?结论:在同圆或等圆中,如果两个圆周角相等,它们所对弧一定相等.因为,在同圆或等圆中,如果圆周角相等,那么它所对的圆心角也相等,因此它所对的弧也相等. 如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm, ?ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长.5.应用解:连接 OD,AD,BD, ∵ AB 是⊙O 的直径,
∴ ?ACB=?ADB=90°.
在 Rt△ABC 中,
BC= = =8(cm) 如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm, ?ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长.5.应用 1.如图,以⊙O的半径OA为直径作⊙O1,⊙O的弦AD交⊙O1于C,则OC与AD的位置关系是_____, OC与BD的位置关系是_____,若AC=2cm,则AD=__cm。垂直平行4随堂练习学科网 3.如图,∠A=50°,∠ABC=60 °,BD是
⊙O的直径,则∠AEB等于( )
A.70° B.110°
C.90° D.120° 2.如图AB,AC为⊙O的两条弦,
延长CA到D,使AD=AB,若∠ADB=300.
则∠BOC=________。EB1200随堂练习zxxkw3. 求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆.)·ABCO已知:△ABC ,CO为AB边上的中线,求证: △ABC 为直角三角形.证明:CO= AB,以AB为直径作⊙O.∵AO=BO, ∴AO=BO=CO.∴点C在⊙O上.又∵AB为⊙O的直径,∴∠ACB= ×180°= 90°.且CO= AB.∴ △ABC 为直角三角形.5、已知⊙O中弦AB的长等于半径,
求弦AB所对的圆心角和圆周角的度数。 圆心角为60度圆周角为 30 度或 150 度。例2 在足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻,当甲带球冲到A点时,乙已跟随冲到B点(如图2).此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好?分析 在真正的足球比赛中情况会很复杂,这里仅用数学方法从两点的静止状态加以考虑,如果两个点到球门的距离相差不大,要确定较好的射门位置,关键看这两个点分别对球门MN的张角大小,当张角较小时,则球容易被对方守门员拦截.怎样比较A、B两点对MN张角的大小呢?解 考虑过M、N以及A、B中的任一点作一圆,这里不妨作出⊙BMN,显然,A点在⊙BMN外,设MA交圆于C,则
∠MAN<∠MCN,而∠MCN=∠MBN,
所以∠MAN<∠MBN.
因此,甲应将球回传给乙,让乙射门.1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.3.在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等。2.半圆或直径所对的圆周角都相等,都等于90°
90°的圆周角所对的弦是圆的直径小结:zxxkwzxxkw 1.如图,以⊙O的半径OA为直径作⊙O1,⊙O的弦AD交⊙O1于C,则OC与AD的位置关系是_____, OC与BD的位置关系是_____,若AC=2cm,则AD=__cm。垂直平行4随堂练习学科网 3.如图,∠A=50°,∠ABC=60 °,BD是
⊙O的直径,则∠AEB等于( )
A.70° B.110°
C.90° D.120° 2.如图AB,AC为⊙O的两条弦,
延长CA到D,使AD=AB,若∠ADB=300.
则∠BOC=________。EB1200随堂练习zxxkw分析:同一条弧所对的圆周角有很多,圆周角的位置灵活多变,可以把注意力放在圆周角所对的弧上.4. 如图,AB是⊙O的直径, C 和D是圆上的两点,若∠ABD=40°,求∠BCD的度数.40°随堂练习例2. 如图,AB为⊙O的一条固定直径,自上半圆上一点C,作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在半圆(不含A,B两点)上移动时,问:点P的位置是否变化?例题讲解分析 连结AO,CO,由勾股定理不难得到△ABD为等腰直角三角形,则∠AOC==90°,又OA=OC,AC长度已知,则可以求出半径和直径. 更一般的情况要用正弦定理来求.OCBAD5. 如图,A,B,C三点在⊙O上,AD⊥BC于D,且AC=5,DC=3,AB= ,求⊙O的直径.随堂练习 1如图,⊙O中,弦DC、AB的延长线相交于点P,如果∠AOD=1200,∠BDC=250,那么
∠P= .350走进中考 2如图,在⊙O中,∠AOB的度数为m.C是∠ACB上
一点,D、E是AB弧上不同的两点
(不与A,B两点重合),则∠D+∠E的度数为( )
A.m B. C. D.走进中考 B 如果一个多边形的所有顶点都在同一个圆上,
这个多边形就叫做圆内接多边形,这个圆叫做这个
多边形的外接圆. 如图,四边形ABCD是⊙O
的内接四边形, ⊙O是四边形
ABCD的外接圆。思考:∠A+∠C=? 能用圆周角定理证明你的结论吗? 圆内接四边形的对角互补。 6.如图,⊙O中,∠A0B = 80o,则∠ACB=____.140oD随堂练习 7.求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆.)·ABCO求证: △ABC 为直角三角形.证明:以AB为直径作⊙O,∵AO=BO, ∴AO=BO=CO.∴点C在⊙O上.又∵AB为直径,∴∠ACB= 90°.∴ △ABC 为直角三角形.CO= AB,随堂练习 1.船在航行过程中,船长常常通过测定角度来测定是否会遇到暗礁,如图表示灯塔,暗礁分布在经过A、B两点的一个圆形区域内,C表示一个危险临界点,∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁。
1)当船与两个灯塔的夹角α大于“危险角”时,船位于哪个区域?为什么?
2)当船与两个灯塔的夹角α
小于“危险角”时,船位于哪个
区域?为什么?
拓展提高 2.如图,在足球比赛中,甲、乙两名队员互相配合向对方球门MN进攻,当甲带球冲到A点时,乙已跟随冲到B点,从数学角度看,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好?
BANMC拓展提高 提示:从数学角度看,甲、乙谁射门好,关键是比较∠MAN与∠MBN的大小,角度越大,射门的机会越好。
zxxkwzxxkw 2.如图,在足球比赛中,甲、乙两名队员互相配合向对方球门MN进攻,当甲带球冲到A点时,乙已跟随冲到B点,从数学角度看,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好?
拓展提高 提示:从数学角度看,甲、乙谁射门好,关键是比较∠MAN与∠MBN的大小,角度越大,射门的机会越好。
3.如图,点P是圆上的一个动点,弦AB= ,PC是∠APB的平分线,∠BAC=300.
(1)当∠PAC等于多少度时四边形PACB有最大面积?最大面积是多少?
(2)当∠PAC等于多少度时四边形PACB是梯形?拓展提高 P1P2P3如图,你能设法确定一个圆形纸片的圆心吗?你有多少种方法?与同学交流一下.DOOO·方法一方法二方法三方法四AB合作交流
同课章节目录
