(苏科版2024)2.5.2有理数的乘法与除法:除法 课件(共17张PPT)
文档属性
| 名称 | (苏科版2024)2.5.2有理数的乘法与除法:除法 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-06 18:43:34 | ||
图片预览






文档简介
(共17张PPT)
第2章 有理数
2.5.2 有理数的乘法与除法:
除法
01
课堂引入
某地某星期每天上午8:00的气温记录如下:
星期一 星期二 星期三 星期四 星期五 星期六 星期日
-4℃ -4℃ 0℃ 1℃ 1℃ -3℃ -5℃
该地该星期每天上午8:00的平均气温(单位:℃)为:
[(-4)+(-4)+0+1+1+(-3)+(-5)]÷7,即(-14)÷7
01
课堂引入
问题——如何计算(-14)÷7?
∵(-2)×7=-14,
∴(-14)÷7=-2。
除以一个数,
乘这个数的倒数。
(-14)÷7=(-14)×=-2
02
知识精讲
一个同学想法的依据是除法的意义,即乘法是除法的逆运算;另一个同学用了小学里学过的除法法则。
他们的想法都是合理的,由此可以得到下面的运算过程:
(-14)÷7=-2
(-14)×=-2
乘以7的倒数
∴(-14)÷7
=(-14)×
=-2
02
知识精讲
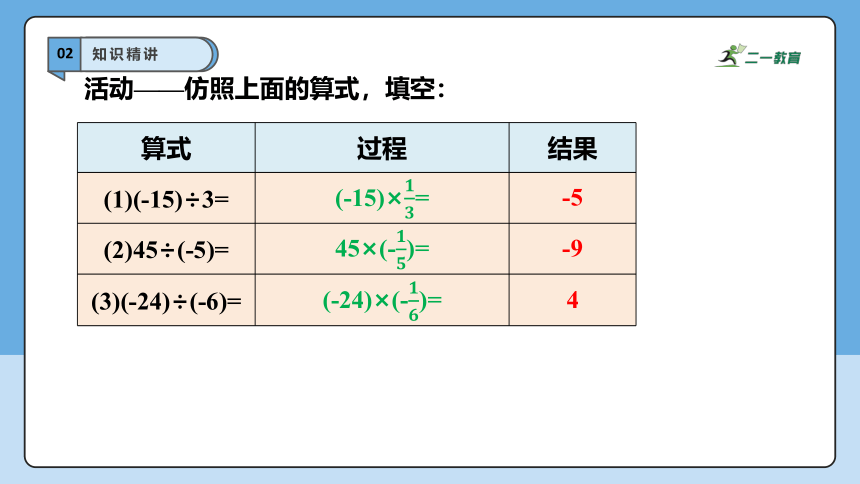
活动——仿照上面的算式,填空:
算式 过程 结果
(1)(-15)÷3=
(2)45÷(-5)=
(3)(-24)÷(-6)=
(-15)×= -5
45×(-)= -9
(-24)×(-)= 4
02
知识精讲
除以一个不等于0的数,等于乘这个数的倒数。
符号语言:a÷b=a×(b≠0)。
02
知识精讲
∵有理数的除法可以转化为乘法,
∴有理数的除法也有下列法则。
1.两个不等于0 的数相除,同号得正,异号得负(定号),并把绝对值相除(定值)。
2.0除以任何一个不等于0的数,都得0。
按照小学里的习惯,两个数相除可以写成分数的形式,即a÷b=。
03
典例分析
例1、计算:(1)0÷(-)
(2)-27÷6
(3)36÷(-3)
(4)(-)÷(-)
0除以任何一个不等于0的数,都得0。
=-=-
36÷(-3)和-有什么关系?
相等,
36÷(-3)=-=-12。
解:(4)原式
=(-)×(-)=+(×)=
=-12
02
知识精讲
例2、计算:(1)(-24)÷12÷(-2) (2)11÷(-2)÷5
(3)(-64)÷×÷(-25) (4)1÷(-)÷(-)÷(-)
不相等,
(-24)÷[12÷(-2)]
=(-24)÷(-6)=4。
(-24)÷12÷(-2)与
(-24)÷[12÷(-2)]相等吗?
解:(1)原式
=(-24)××(-)
=+(24××)
=1
03
典例分析
例2、计算:(1)(-24)÷12÷(-2) (2)11÷(-2)÷5
(3)1÷(-)÷(-)÷(-)
(2)原式
=11÷(-)÷5
=11×(-)×
=-(11××)
=-1
(3)原式
=÷(-)÷(-)÷(-)
=×(-)×(-)×(-)
=-(×××)
=-1
03
典例分析
例3、计算:(1-+-+-)÷(-)
解:原式
=(1-+-+-)×(-60)
=1×(-60)+(-)×(-60)+×(-60)+(-)×(-60)+×(-60)+(-)×(-60)
=(-60)+30+(-20)+15+(-12)+10
=-37
03
典例分析
例4、计算:(1)÷(-+) (2)(-)÷(-+-)
解:(1)【法一】原式=÷=÷=×6=
【法二】原式的倒数=(-+)÷
=(-+)×24=×24+(-)×24+×24=8+(-6)+2=4
∴原式=
03
典例分析
例5、混合计算:(1)÷(-5)÷(-)×5 (2)(-64)÷×÷(-25)
(3)2÷(-)×÷(-5) (4) (+5)÷(-4)×(-)÷(-3)
解:(1)原式
=×(-)×(-5)×5
=+(××5×5)
=1
(2)原式
=(-64)×××(-)
=+(64×××)
=1
03
典例分析
例6、混合计算:(-)×(-3)÷|-1|×(-2)
有绝对值先算绝对值
解:原式=(-)×(-3)÷×(-2)
=(-)×(-3)××(-2)
=-(×3××2)
=-
04
课后总结
有理数除法法则升级版:
1.两个不等于0 的数相除,同号得正,异号得负(定号),并把绝对值相除(定值)。
2.0除以任何一个不等于0的数,都得0。
有理数除法法则:
除以一个不等于0的数,等于乘这个数的倒数。
符号语言:a÷b=a×(b≠0)。
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第2章 有理数
2.5.2 有理数的乘法与除法:
除法
01
课堂引入
某地某星期每天上午8:00的气温记录如下:
星期一 星期二 星期三 星期四 星期五 星期六 星期日
-4℃ -4℃ 0℃ 1℃ 1℃ -3℃ -5℃
该地该星期每天上午8:00的平均气温(单位:℃)为:
[(-4)+(-4)+0+1+1+(-3)+(-5)]÷7,即(-14)÷7
01
课堂引入
问题——如何计算(-14)÷7?
∵(-2)×7=-14,
∴(-14)÷7=-2。
除以一个数,
乘这个数的倒数。
(-14)÷7=(-14)×=-2
02
知识精讲
一个同学想法的依据是除法的意义,即乘法是除法的逆运算;另一个同学用了小学里学过的除法法则。
他们的想法都是合理的,由此可以得到下面的运算过程:
(-14)÷7=-2
(-14)×=-2
乘以7的倒数
∴(-14)÷7
=(-14)×
=-2
02
知识精讲
活动——仿照上面的算式,填空:
算式 过程 结果
(1)(-15)÷3=
(2)45÷(-5)=
(3)(-24)÷(-6)=
(-15)×= -5
45×(-)= -9
(-24)×(-)= 4
02
知识精讲
除以一个不等于0的数,等于乘这个数的倒数。
符号语言:a÷b=a×(b≠0)。
02
知识精讲
∵有理数的除法可以转化为乘法,
∴有理数的除法也有下列法则。
1.两个不等于0 的数相除,同号得正,异号得负(定号),并把绝对值相除(定值)。
2.0除以任何一个不等于0的数,都得0。
按照小学里的习惯,两个数相除可以写成分数的形式,即a÷b=。
03
典例分析
例1、计算:(1)0÷(-)
(2)-27÷6
(3)36÷(-3)
(4)(-)÷(-)
0除以任何一个不等于0的数,都得0。
=-=-
36÷(-3)和-有什么关系?
相等,
36÷(-3)=-=-12。
解:(4)原式
=(-)×(-)=+(×)=
=-12
02
知识精讲
例2、计算:(1)(-24)÷12÷(-2) (2)11÷(-2)÷5
(3)(-64)÷×÷(-25) (4)1÷(-)÷(-)÷(-)
不相等,
(-24)÷[12÷(-2)]
=(-24)÷(-6)=4。
(-24)÷12÷(-2)与
(-24)÷[12÷(-2)]相等吗?
解:(1)原式
=(-24)××(-)
=+(24××)
=1
03
典例分析
例2、计算:(1)(-24)÷12÷(-2) (2)11÷(-2)÷5
(3)1÷(-)÷(-)÷(-)
(2)原式
=11÷(-)÷5
=11×(-)×
=-(11××)
=-1
(3)原式
=÷(-)÷(-)÷(-)
=×(-)×(-)×(-)
=-(×××)
=-1
03
典例分析
例3、计算:(1-+-+-)÷(-)
解:原式
=(1-+-+-)×(-60)
=1×(-60)+(-)×(-60)+×(-60)+(-)×(-60)+×(-60)+(-)×(-60)
=(-60)+30+(-20)+15+(-12)+10
=-37
03
典例分析
例4、计算:(1)÷(-+) (2)(-)÷(-+-)
解:(1)【法一】原式=÷=÷=×6=
【法二】原式的倒数=(-+)÷
=(-+)×24=×24+(-)×24+×24=8+(-6)+2=4
∴原式=
03
典例分析
例5、混合计算:(1)÷(-5)÷(-)×5 (2)(-64)÷×÷(-25)
(3)2÷(-)×÷(-5) (4) (+5)÷(-4)×(-)÷(-3)
解:(1)原式
=×(-)×(-5)×5
=+(××5×5)
=1
(2)原式
=(-64)×××(-)
=+(64×××)
=1
03
典例分析
例6、混合计算:(-)×(-3)÷|-1|×(-2)
有绝对值先算绝对值
解:原式=(-)×(-3)÷×(-2)
=(-)×(-3)××(-2)
=-(×3××2)
=-
04
课后总结
有理数除法法则升级版:
1.两个不等于0 的数相除,同号得正,异号得负(定号),并把绝对值相除(定值)。
2.0除以任何一个不等于0的数,都得0。
有理数除法法则:
除以一个不等于0的数,等于乘这个数的倒数。
符号语言:a÷b=a×(b≠0)。
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
