(苏科版2024)2.6有理数的乘方 课件(共40张PPT)
文档属性
| 名称 | (苏科版2024)2.6有理数的乘方 课件(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-06 18:44:19 | ||
图片预览









文档简介
(共40张PPT)
第2章 有理数
2.6 有理数的乘方
01
教学目标
01
从实际问题情境认识并理解乘方的概念
03
能正确使用科学记数法表示数
02
探索乘方的性质,并能灵活运用性质进行运算
02
课堂引入
小故事——无法实施的奖赏
国际象棋起源于印度,棋盘上共有8行8列,构成64个格子。
传说国王要奖赏国际象棋的发明者,他的大宰相西萨·班·达伊尔,问他有什么要求~
这位聪明的大宰相的胃口并不是太大,他跪在国王面前说,“皇帝陛下,请在棋盘的第1个格子里放上1颗麦粒,在棋盘的第2个格子里放上2颗麦粒,在棋盘的3个格子里放上4颗麦粒,在棋盘的4个格子里放上8颗麦粒,以此类推。每个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到第64个格子。”
02
课堂引入
国王听了很不以为然,说,“爱卿,你的要求并不多,我一定满足你的要求!”
没过一会儿,他的粮管就来报告了,“国王,不对,我们整个国家的粮库的粮食都才能摆到30格。如果满足他这个要求,我们国家要全国不吃不喝种2000多年!”
你知道为什么吗?
02
课堂引入
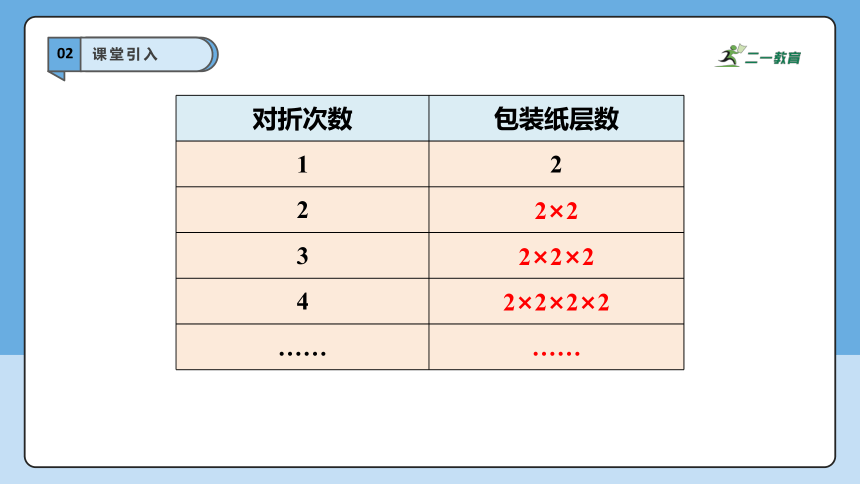
问题——将一张包装纸对折,再对折……直到无法对折为止,你对折了多少次?请用算式表示对折后得到的包装纸层数。
大多人是能对折6次或7次。
∵每次对折后包装纸的层数都变成原来的2倍,
∴包装纸层数与对折次数之间具有下面的关系:
02
课堂引入
对折次数 包装纸层数
1 2
2 2×2
3 2×2×2
4 2×2×2×2
…… ……
03
知识精讲
我们知道,同一个加数连续相加可以用乘法表示,如2+2=2×2,2+2+2=2×3,2+2+2+2=2×4,…
类似地,同一个因数的积也可以用一种简便形式表示,如2×2=22,读作“2的平方”,2×2×2=23,读作“2的3次方”,2×2×2×2=24,读作“2的4次方”……
03
知识精讲
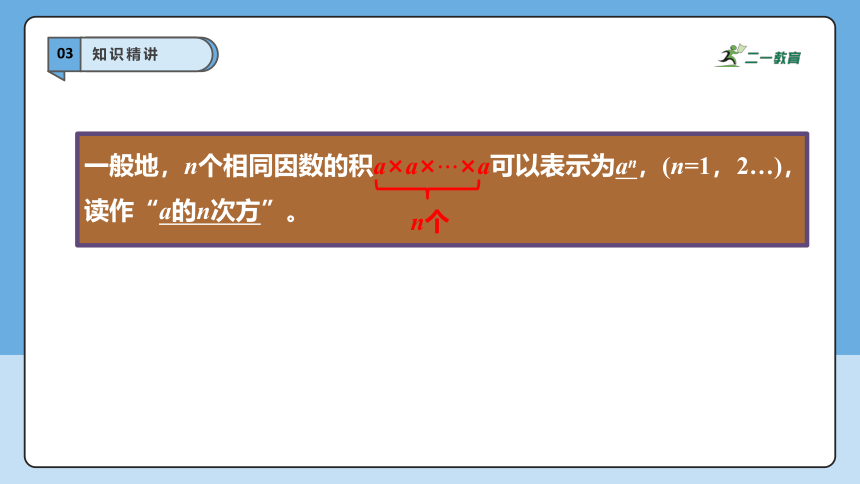
一般地,n个相同因数的积a×a××a可以表示为an,(n=1,2…),读作“a的n次方”。
n个
03
知识精讲
求相同因数的积的运算叫作乘方,相同因数叫作底数,相同因数的个数叫作指数,乘方运算的结果叫作幂。
乘方运算本质上是乘法运算,它是同一个因数连乘的简便形式。
幂
底数:相同因数a
指数:相同因数的个数n
an
03
知识精讲
eg:26表示乘方运算(即6个2相乘)时,读作“2的6次方”,2是底数,6是指数;
注意区分乘方与幂 乘方 一种运算
幂 这种运算的结果
如果把26看作乘方运算的结果(即64),这时它表示一个数,读作读作“2的6次幂”。
03
知识精讲
问题解决——无法实施的奖赏
格子序号 麦粒数(颗)
1 1
2 2
3 22
4 23
… …
64 263
263=9223372036854775808
04
典例精析
例1、(1)4个9相乘记为____,9是____,4是____,读作________;
(2)7个相乘记为____,底数是____,指数是____,读作________;
(3)5个-3相乘记为____,底数是____,指数是____,读作________.
94
底数
指数
9的4次方
7
的7次方
(-3)5
-3
5
-3的5次方
04
典例精析
过程 结果
34
(-3)4
-34
例2-1、计算:
3×3×3×3= 81
(-3)×(-3)×(-3)×(-3)= 81
-(3×3×3×3)= -81
注意区分(-3)4和-34:
(-3)4是4个(-3)相乘,读作“3的4次方”;
-34是34的相反数,读作“3的4次方的相反数”。
04
典例精析
过程 结果
(-)3
-
例2-2、计算:
(-)×(-)×(-)= -
=×(-2)3
×[(-2)×(-2)×(-2)] -
-=-×23
-×(2×2×2) -
04
典例精析
例3、下列运算结果是负数的是________________.
(1)-22
(2)(-2)2
(3)-(-2)2
(4)-23
(5)(-2)3
(6)-(-2)3
=-(2×2)=-4
=(-2)×(-2)=4
=-[(-2)×(-2)]=-4
=-2×2×2=-8
=(-2)×(-2)×(-2)=-8
=-[(-2)×(-2)×(-2)]=8
(1)(3)(4)(5)
乘方的性质
01
课堂引入
探究——1.(-1)10,(-7)13,(-)6,(-)7是正数还是负数?
结果的正负情况和什么有关?
(-1)10=(-1)×(-1)×(-1)×(-1)×(-1)×(-1)×(-1)×(-1)×(-1)×(-1)=1>0
(-7)13=13个(-7)相乘<0
(-)6=(-)×(-)×(-)×(-)×(-)×(-)=>0
(-)7=(-)×(-)×(-)×(-)×(-)×(-)×(-)=-<0
结果的正负与指数的奇偶有关
01
课堂引入
当n是偶数时,(-1)n=1;当n是奇数时,(-1)n=-1.
2.当n是偶数时,(-1)n等于多少?当n是奇数时,(-1)n等于多少?
3.01等于多少?0520等于多少?01314等于多少?
都等于0
02
知识精讲
讨论——1.算一算,找规律
结果 结果
199 1 (-1)99 -1
29 (-2)9
35 (-3)5
43 (-4)3
0521 0 0521 0
互为相反数的两个数的奇数次幂互为相反数
243 -243
512 -512
64 -64
02
知识精讲
2.算一算,找规律~
结果 结果
1100 1 (-1)100 1
210 (-2)100
36 (-3)6
44 (-4)4
0520 0 0520 0
1024 1024
729 729
互为相反数的两个数的偶数次幂相等
256 256
一个数的偶数次幂具有非负性
02
知识精讲
互为相反数的两个数的奇数次幂互为相反数;
互为相反数的两个数的偶数次幂相等,一个数的偶数次幂具有非负性。
03
典例精析
例1、填空:
平方等于它本身的数是_____,立方等于它本身的数是_____。
0或1
0或±1
03
典例精析
注意:(-2)4≠-24
(-2)4=(-2)×(-2)×(-2)×(-2)=16;
-24是24的相反数,
-24=-(2×2×2×2)=-16。
解:(1)原式=16×(-27)=-432
(2)原式=-16+8+(-1)=-9
例2、计算:
(1)(-2)4×(-3)3
(2)-24+23+(-1)123456789
03
典例精析
解:(1)原式=32156-32156=0
例3、(1)计算:(-321)56-32156
(2)计算:299-(-2)99
(3)已知(a+19)4+(b-2)100=0,求ab
(2)原式=299-(-299)=299+299=299×2=2100
(3)由“偶数幂的非负性”可知:(a+19)4=0,(b-2)100=0,
∴a+19=0,b-2=0,解得:a=-19,b=2,
∴ab=(-19)2=361
科学计数法
01
课堂引入
光的传播速度大约是300 000 000米/秒;
而声音在常温下的传播速度大约是340米/秒。
为什么打雷时,“先见闪电,后闻雷声”
01
课堂引入
地球半径约为6 400 000米;
赤道长约为40 000 000米;
地球表面积为510 000 000 000 000平方米。
01
课堂引入
第七次人口普查的结果如下:
全国总人口为1443497378人,其中:
普查登记的大陆31个省、自治区、直辖市和现役军人的人口共1411778724人;
香港特别行政区人口为7474200人;
澳门特别行政区人口为683218人;
台湾地区人口为23561236人。
01
课堂引入
数大
不方便记数
01
课堂引入
活动——1.新生儿的大脑约有100 000 000 000个神经元。将100 000 000 000输入计算器,再按“=”键,计算器如何显示?
2.北极星距离地球大约4 100 000 000 000 000km。将4 100 000 000 000 000输入计算器,再按“=”键,计算器如何显示?
3.用计算器计算-8 000 000×600 000 000,计算器如何显示?
02
知识精讲
像这些较大的数通常用如下的方法简明地表示:
100 000 000 000=1×1011;
4 100 000 000 000 000=4.1×1 000 000 000 000 000=4.1×1015;
-8 000 000×600 000 000= -4 800 000 000 000 000
=-4.8×1 000 000 000 000 000=-4.8×1015。
02
知识精讲
一般地,一个绝对值大于10的数可以写成a×10n的形式,其中1≤|a|<10,n为正整数,这种记数方法称为科学记数法。
当a=1时,可简写成10n。
02
知识精讲
问题解决——用科学记数法表示下列各数:
(1)光的传播速度大约是300 000 000米/秒;
(2)地球半径约为6 400 000米,赤道长约为40 000 000米,地球表面积为510 000 000 000 000平方米;
(3)(第七次人口普查)全国总人口为1443497378人。
【分析】(1)300 000 000=3×108;
(2)6 400 000=6.4×106,
40 000 000=4×107,
510 000 000 000 000=5.1×1014;
(3)1443497378=1.443497378×109。
03
典例精析
例1、经专家估算,我国南海的油气资源约合15000亿美元,开采前景甚至要超过英国的北海油田,用科学记数法表示15000亿美元是________美元。
1.5×1012
03
典例精析
例2、写出下列用科学记数法记数的原数:
(1)1.381×103;
(2)-9.23×105;
(3)2.009×106;
1381
-923000
2009000
03
典例精析
例3、一天有8.64×104秒,一年如果按365天计算,一年有多少秒?(用科学记数法表示)
解:8.64×104×365
=8.64×365×104
=3153.6×104
=3.1536×107
答:一年有3.1536×107秒。
04
课后总结
乘方的概念:
一般地,n个相同因数的积a×a××a可以表示为an,(n=1,2…),读作“a的n次方”。
求相同因数的积的运算叫作乘方,相同因数叫作底数,相同因数的个数叫作指数,乘方运算的结果叫作幂。
n个
04
课后总结
乘方的性质:
正数的任何次幂都是正数;
负数的奇次幂是负数,负数的偶次幂是正数;
0的任何正数次幂都是0。
互为相反数的两个数的奇数次幂互为相反数;
互为相反数的两个数的偶数次幂相等,一个数的偶数次幂具有非负性。
一般地,一个绝对值大于10的数可以写成a×10n的形式,其中1≤|a|<10,n为正整数,这种记数方法称为科学记数法。
当a=1时,可简写成10n。
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第2章 有理数
2.6 有理数的乘方
01
教学目标
01
从实际问题情境认识并理解乘方的概念
03
能正确使用科学记数法表示数
02
探索乘方的性质,并能灵活运用性质进行运算
02
课堂引入
小故事——无法实施的奖赏
国际象棋起源于印度,棋盘上共有8行8列,构成64个格子。
传说国王要奖赏国际象棋的发明者,他的大宰相西萨·班·达伊尔,问他有什么要求~
这位聪明的大宰相的胃口并不是太大,他跪在国王面前说,“皇帝陛下,请在棋盘的第1个格子里放上1颗麦粒,在棋盘的第2个格子里放上2颗麦粒,在棋盘的3个格子里放上4颗麦粒,在棋盘的4个格子里放上8颗麦粒,以此类推。每个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到第64个格子。”
02
课堂引入
国王听了很不以为然,说,“爱卿,你的要求并不多,我一定满足你的要求!”
没过一会儿,他的粮管就来报告了,“国王,不对,我们整个国家的粮库的粮食都才能摆到30格。如果满足他这个要求,我们国家要全国不吃不喝种2000多年!”
你知道为什么吗?
02
课堂引入
问题——将一张包装纸对折,再对折……直到无法对折为止,你对折了多少次?请用算式表示对折后得到的包装纸层数。
大多人是能对折6次或7次。
∵每次对折后包装纸的层数都变成原来的2倍,
∴包装纸层数与对折次数之间具有下面的关系:
02
课堂引入
对折次数 包装纸层数
1 2
2 2×2
3 2×2×2
4 2×2×2×2
…… ……
03
知识精讲
我们知道,同一个加数连续相加可以用乘法表示,如2+2=2×2,2+2+2=2×3,2+2+2+2=2×4,…
类似地,同一个因数的积也可以用一种简便形式表示,如2×2=22,读作“2的平方”,2×2×2=23,读作“2的3次方”,2×2×2×2=24,读作“2的4次方”……
03
知识精讲
一般地,n个相同因数的积a×a××a可以表示为an,(n=1,2…),读作“a的n次方”。
n个
03
知识精讲
求相同因数的积的运算叫作乘方,相同因数叫作底数,相同因数的个数叫作指数,乘方运算的结果叫作幂。
乘方运算本质上是乘法运算,它是同一个因数连乘的简便形式。
幂
底数:相同因数a
指数:相同因数的个数n
an
03
知识精讲
eg:26表示乘方运算(即6个2相乘)时,读作“2的6次方”,2是底数,6是指数;
注意区分乘方与幂 乘方 一种运算
幂 这种运算的结果
如果把26看作乘方运算的结果(即64),这时它表示一个数,读作读作“2的6次幂”。
03
知识精讲
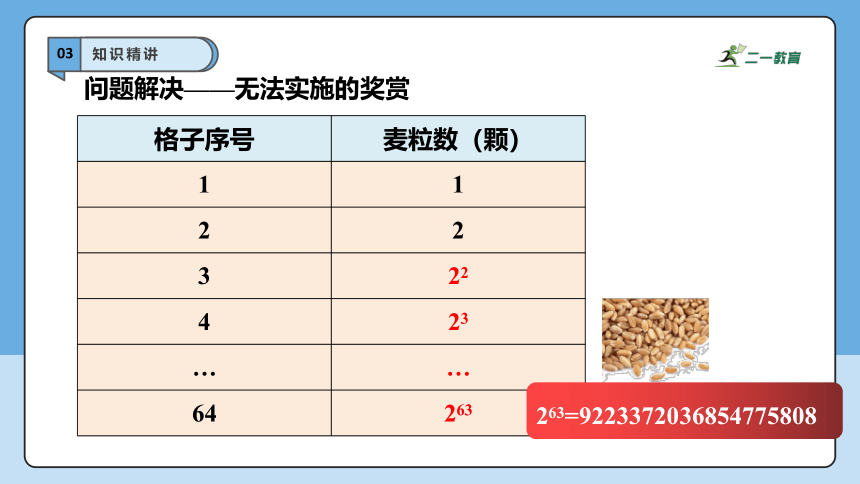
问题解决——无法实施的奖赏
格子序号 麦粒数(颗)
1 1
2 2
3 22
4 23
… …
64 263
263=9223372036854775808
04
典例精析
例1、(1)4个9相乘记为____,9是____,4是____,读作________;
(2)7个相乘记为____,底数是____,指数是____,读作________;
(3)5个-3相乘记为____,底数是____,指数是____,读作________.
94
底数
指数
9的4次方
7
的7次方
(-3)5
-3
5
-3的5次方
04
典例精析
过程 结果
34
(-3)4
-34
例2-1、计算:
3×3×3×3= 81
(-3)×(-3)×(-3)×(-3)= 81
-(3×3×3×3)= -81
注意区分(-3)4和-34:
(-3)4是4个(-3)相乘,读作“3的4次方”;
-34是34的相反数,读作“3的4次方的相反数”。
04
典例精析
过程 结果
(-)3
-
例2-2、计算:
(-)×(-)×(-)= -
=×(-2)3
×[(-2)×(-2)×(-2)] -
-=-×23
-×(2×2×2) -
04
典例精析
例3、下列运算结果是负数的是________________.
(1)-22
(2)(-2)2
(3)-(-2)2
(4)-23
(5)(-2)3
(6)-(-2)3
=-(2×2)=-4
=(-2)×(-2)=4
=-[(-2)×(-2)]=-4
=-2×2×2=-8
=(-2)×(-2)×(-2)=-8
=-[(-2)×(-2)×(-2)]=8
(1)(3)(4)(5)
乘方的性质
01
课堂引入
探究——1.(-1)10,(-7)13,(-)6,(-)7是正数还是负数?
结果的正负情况和什么有关?
(-1)10=(-1)×(-1)×(-1)×(-1)×(-1)×(-1)×(-1)×(-1)×(-1)×(-1)=1>0
(-7)13=13个(-7)相乘<0
(-)6=(-)×(-)×(-)×(-)×(-)×(-)=>0
(-)7=(-)×(-)×(-)×(-)×(-)×(-)×(-)=-<0
结果的正负与指数的奇偶有关
01
课堂引入
当n是偶数时,(-1)n=1;当n是奇数时,(-1)n=-1.
2.当n是偶数时,(-1)n等于多少?当n是奇数时,(-1)n等于多少?
3.01等于多少?0520等于多少?01314等于多少?
都等于0
02
知识精讲
讨论——1.算一算,找规律
结果 结果
199 1 (-1)99 -1
29 (-2)9
35 (-3)5
43 (-4)3
0521 0 0521 0
互为相反数的两个数的奇数次幂互为相反数
243 -243
512 -512
64 -64
02
知识精讲
2.算一算,找规律~
结果 结果
1100 1 (-1)100 1
210 (-2)100
36 (-3)6
44 (-4)4
0520 0 0520 0
1024 1024
729 729
互为相反数的两个数的偶数次幂相等
256 256
一个数的偶数次幂具有非负性
02
知识精讲
互为相反数的两个数的奇数次幂互为相反数;
互为相反数的两个数的偶数次幂相等,一个数的偶数次幂具有非负性。
03
典例精析
例1、填空:
平方等于它本身的数是_____,立方等于它本身的数是_____。
0或1
0或±1
03
典例精析
注意:(-2)4≠-24
(-2)4=(-2)×(-2)×(-2)×(-2)=16;
-24是24的相反数,
-24=-(2×2×2×2)=-16。
解:(1)原式=16×(-27)=-432
(2)原式=-16+8+(-1)=-9
例2、计算:
(1)(-2)4×(-3)3
(2)-24+23+(-1)123456789
03
典例精析
解:(1)原式=32156-32156=0
例3、(1)计算:(-321)56-32156
(2)计算:299-(-2)99
(3)已知(a+19)4+(b-2)100=0,求ab
(2)原式=299-(-299)=299+299=299×2=2100
(3)由“偶数幂的非负性”可知:(a+19)4=0,(b-2)100=0,
∴a+19=0,b-2=0,解得:a=-19,b=2,
∴ab=(-19)2=361
科学计数法
01
课堂引入
光的传播速度大约是300 000 000米/秒;
而声音在常温下的传播速度大约是340米/秒。
为什么打雷时,“先见闪电,后闻雷声”
01
课堂引入
地球半径约为6 400 000米;
赤道长约为40 000 000米;
地球表面积为510 000 000 000 000平方米。
01
课堂引入
第七次人口普查的结果如下:
全国总人口为1443497378人,其中:
普查登记的大陆31个省、自治区、直辖市和现役军人的人口共1411778724人;
香港特别行政区人口为7474200人;
澳门特别行政区人口为683218人;
台湾地区人口为23561236人。
01
课堂引入
数大
不方便记数
01
课堂引入
活动——1.新生儿的大脑约有100 000 000 000个神经元。将100 000 000 000输入计算器,再按“=”键,计算器如何显示?
2.北极星距离地球大约4 100 000 000 000 000km。将4 100 000 000 000 000输入计算器,再按“=”键,计算器如何显示?
3.用计算器计算-8 000 000×600 000 000,计算器如何显示?
02
知识精讲
像这些较大的数通常用如下的方法简明地表示:
100 000 000 000=1×1011;
4 100 000 000 000 000=4.1×1 000 000 000 000 000=4.1×1015;
-8 000 000×600 000 000= -4 800 000 000 000 000
=-4.8×1 000 000 000 000 000=-4.8×1015。
02
知识精讲
一般地,一个绝对值大于10的数可以写成a×10n的形式,其中1≤|a|<10,n为正整数,这种记数方法称为科学记数法。
当a=1时,可简写成10n。
02
知识精讲
问题解决——用科学记数法表示下列各数:
(1)光的传播速度大约是300 000 000米/秒;
(2)地球半径约为6 400 000米,赤道长约为40 000 000米,地球表面积为510 000 000 000 000平方米;
(3)(第七次人口普查)全国总人口为1443497378人。
【分析】(1)300 000 000=3×108;
(2)6 400 000=6.4×106,
40 000 000=4×107,
510 000 000 000 000=5.1×1014;
(3)1443497378=1.443497378×109。
03
典例精析
例1、经专家估算,我国南海的油气资源约合15000亿美元,开采前景甚至要超过英国的北海油田,用科学记数法表示15000亿美元是________美元。
1.5×1012
03
典例精析
例2、写出下列用科学记数法记数的原数:
(1)1.381×103;
(2)-9.23×105;
(3)2.009×106;
1381
-923000
2009000
03
典例精析
例3、一天有8.64×104秒,一年如果按365天计算,一年有多少秒?(用科学记数法表示)
解:8.64×104×365
=8.64×365×104
=3153.6×104
=3.1536×107
答:一年有3.1536×107秒。
04
课后总结
乘方的概念:
一般地,n个相同因数的积a×a××a可以表示为an,(n=1,2…),读作“a的n次方”。
求相同因数的积的运算叫作乘方,相同因数叫作底数,相同因数的个数叫作指数,乘方运算的结果叫作幂。
n个
04
课后总结
乘方的性质:
正数的任何次幂都是正数;
负数的奇次幂是负数,负数的偶次幂是正数;
0的任何正数次幂都是0。
互为相反数的两个数的奇数次幂互为相反数;
互为相反数的两个数的偶数次幂相等,一个数的偶数次幂具有非负性。
一般地,一个绝对值大于10的数可以写成a×10n的形式,其中1≤|a|<10,n为正整数,这种记数方法称为科学记数法。
当a=1时,可简写成10n。
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
