福建省闽清县天儒中学(人教版)数学九年级上册课件:25-3 用频率估计概率(共35张PPT)
文档属性
| 名称 | 福建省闽清县天儒中学(人教版)数学九年级上册课件:25-3 用频率估计概率(共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 463.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-06 00:00:00 | ||
图片预览








文档简介
课件35张PPT。25.3 利用频率估计概率 用列举法求概率等可能性事件1。所有的结果是有限多个
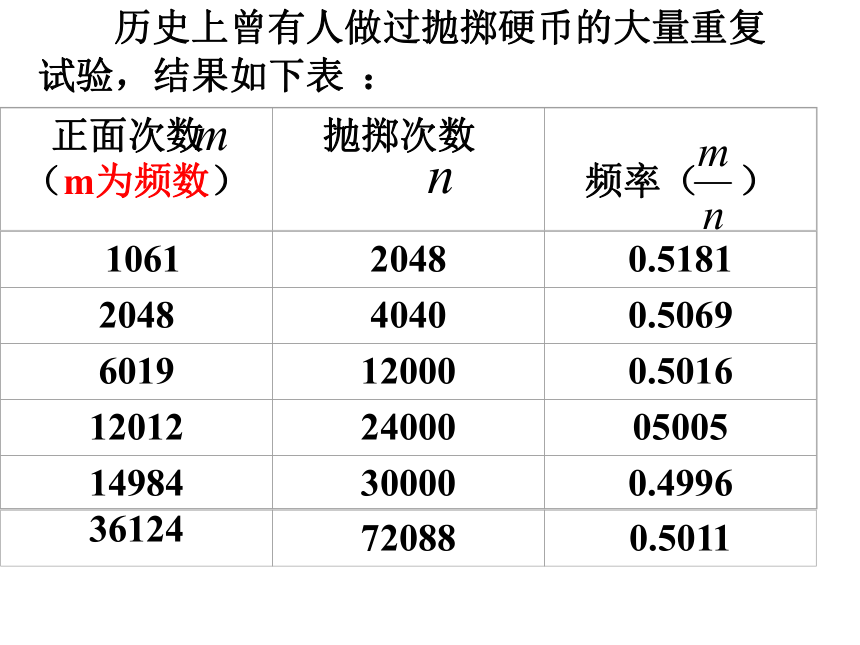
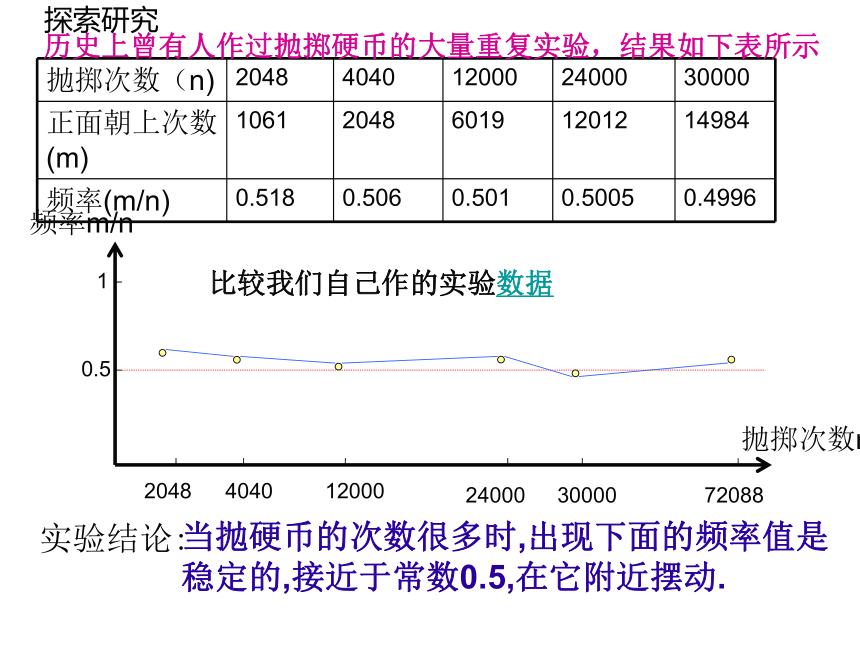
2。各种结果发生的可能性相等。 复习巩固 但在我们的身边,有很多试验的所有可能性是不相等且结果不是有限多个,这些事件的概率怎样确定呢? 提出问题 在同样条件下,通过大量反复的试验,根据一个随机事件发生的频率所逐渐稳定到的常数,可以估计这个事件发生的概率。 历史上曾有人做过抛掷硬币的大量重复试验,结果如下表 :历史上曾有人作过抛掷硬币的大量重复实验,结果如下表所示比较我们自己作的实验数据探索研究实验结论:当抛硬币的次数很多时,出现下面的频率值是
稳定的,接近于常数0.5,在它附近摆动. 当抛掷硬币的次数很多时,出现正面的频率值是稳定的,接近于常数0.5,在它附近摆动. 随机事件及其概率很多 稳定常数 随机事件在一次试验中是否
发生虽然不能事先确定,但是在
大量重复试验的情况下,它的发
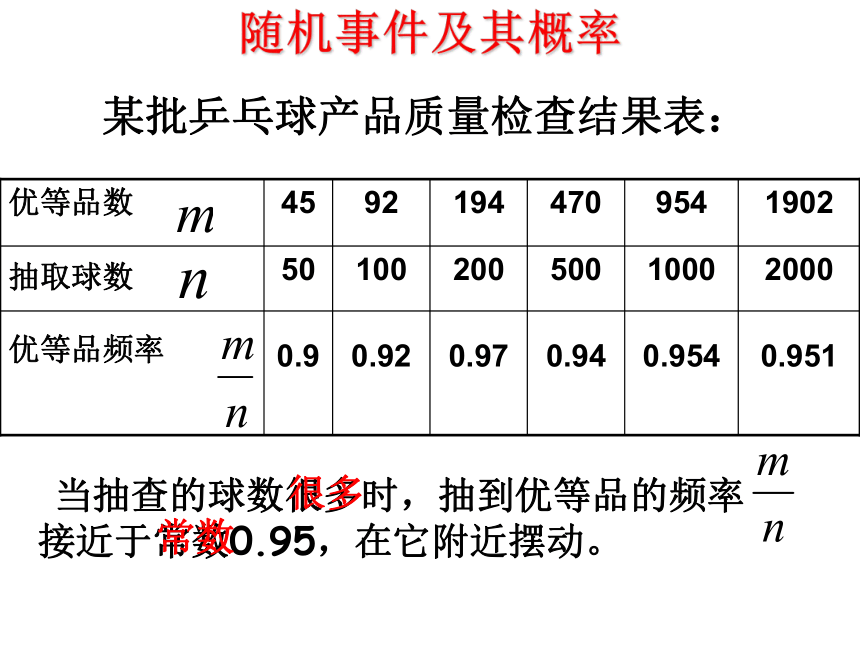
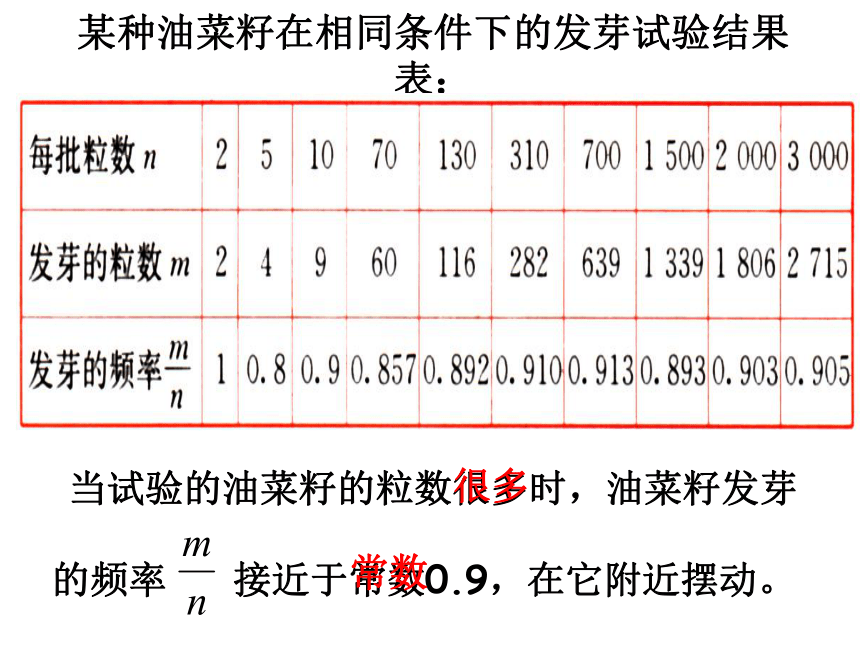
生呈现出一定的规律性.出现的频率值接近于常数.随机事件及其概率某批乒乓球产品质量检查结果表: 当抽查的球数很多时,抽到优等品的频率 接近于常数0.95,在它附近摆动。 很多常数某种油菜籽在相同条件下的发芽试验结果表: 当试验的油菜籽的粒数很多时,油菜籽发芽
的频率 接近于常数0.9,在它附近摆动。很多 常数随机事件及其概率事件 的概率的定义: 一般地,在大量重复进行同一试验时,事件 发生的频率 (n为实验的次数,m是事件发生的频数)总是接近于某个常数,在它附近摆动,这时就把这个常数叫做事件 的概率,记做 . 由定义可知: (1)求一个事件的概率的基本方法是通过大量的重复试验; (3)概率是频率的稳定值,而频率是概率的近似值; (4)概率反映了随机事件发生的可能性的大小; (5)必然事件的概率为1,不可能事件的概率为0.因此 . (2)只有当频率在某个常数附近摆动时,这个常数才叫做事件A 的概率; 某林业部门要考查某种幼树在一定条件的移植成活率,应采用什么具体的做法? 答:在同样条件下,大量地对这种幼树进行移植,并统计成活情况,计算成活的频率。如果随着移植棵数n的越来越大,频率 越来越稳定于某个常数,那么这个常数就可以被当作成活率的近似值。0.9230.8830.9050.897下图是一张模拟的统计表,请补出表中的空缺所以估计幼树移植成活的概率是 。0.90556 某水果公司以2元/千克的成本新进了10000千克的柑橘,如果公司希望这些柑橘能够获利5000元,那么在出售柑橘(已去掉损坏的柑橘)时,每千克大约定价为多少元比较合适? 问题20.1030.1010.098柑橘在运输途中会有些损坏,公司必须估算出可能损坏的柑橘总数,以便将损坏的柑橘成本折算到没有损坏的柑橘的售价中。销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行了“柑橘损坏率”的统计,把获得的数据记录在下:0.100.0990.1030.0970.0970.90某种小麦播种的发芽概率约是95%,1株麦芽长成麦苗的概率约是90%,一块试验田的麦苗数是8550株,该麦种的千粒质量为35千克,则播种这块试验田需麦种约 千克。概率是个准确值
频率是个估计值
通过大量的实验可以使频率趋于一个稳定的常数,用该常数估计概率
实验的次数越多越趋近于概率,因此用实验次数多的频率趋近的常数来估计概率较为精确
归纳4.表中是一个机器人做9999次“抛硬币”游戏时记录下的出现正面的频数和频率. (1)由这张频数和频率表可知,机器人抛掷完5次时,得到1次正面,正面出现的频率是20%,那么,也就是说机器人抛掷完5次时,得到______次反面,反面出现的频率是______.
480% (2)由这张频数和频率表可知,机器人抛掷完9999次时,得到______次正面,正面出现的频率是______.那么,也就是说机器人抛掷完9999次时,得到_______次反面,反面出现的频率是________.
500650.1% 499449.9% 5.给出以下结论,错误的有( )
①如果一件事发生的机会只有十万分之一,那么它就不可能发生. ②如果一件事发生的机会达到99.5%,那么它就必然发生. ③如果一件事不是不可能发生的,那么它就必然发生. ④如果一件事不是必然发生的,那么它就不可能发生.
A.1个 B.2个 C.3个 D.4个
D6.一位保险推销员对人们说:“人有可能得病,也有可能不得病,因此,得病与不得病的概率各占50%”他的说法( )
A.正确 B.不正确
C.有时正确,有时不正确
D.应由气候等条件确定
B7.某位同学一次掷出三个骰子三个全是“6”的事件是( )
A.不可能事件 B.必然事件
C.不确定事件可能性较大
D.不确定事件可能性较小
?
D9.现有3张牌,利用这3张牌:(1).从中抽一张牌,在未抽牌之前分别说出一件有关抽牌的必然事件,不可能事件,不确定事件.(2).任意抽一张牌,抽到的牌数字有几种可能?10.笼子里关着一只兔子(如图),兔子的主人决定把兔子放归大自然,将笼子所有的门都打开。兔子要先经过第一道(A,B,C),再经过第二道门(D或E)才能出去。问兔子走出笼子的路线(经过的两道门)有多少种不同的可能? 用1(或100%)来表示
必然事件发生的可能性,即概率为1;用0来表示不可能事件发生的可能性。即概率为0;必然事件发生的可能性是100%即概率为1;不可能事件发生的可能性是0;不确定事件发生的可能性是大于0而小于1的.即概率为0;即此时概率为小结1.随机事件的概念2.随机事件的概率的定义 在一定条件下可能发生也可能不发生的事件,叫做随机事件. 在大量重复进行同一试验时, 事件 发生的频率 总是接近于某个常数,在它附近摆动,这时就把这个常数叫做事件 的概率.1. 概率的获取有 和 两种。2. 本节课的事件概率无法用理论计算来解决,只能通过概率实验,用 来估算。理论计算实验估算频率2.某射手在同一条件下进行射击,结果如下表所示:(1)计算表中击中靶心的各个频率;
(2)这个射击一次,击中靶心的概率约是多少? 问题情景: 小明参加夏令营,一天夜里熄灯了,伸手不见五指,想到明天去八达岭长城天不亮就出发,想把袜子准备好,而现在又不能开灯。袋子里有尺码相同的3双黑袜子和1双白袜子,混放在一起,只能摸黑去拿出2只。同学们能否求出摸出的2只恰好是一双的可能性?同学们能否通过实验估计它们恰好是一双的可能性?如果手边没有袜子应该怎么办?
问题3一个学习小组有6名男生3名女生。老师要从小组的学生中先后随机地抽取3人参加几项测试,并且每名学生都可被重复抽取。你能设计一种实验来估计“被抽取的3人中有2名男生1名女生”的概率的吗?模拟实验下面的表中给出了一些模拟实验的方法,你觉得这些方法合理吗?若不合理请说明理由请分析下面的表中给出了一些模拟实验的方法,你觉得这些方法合理吗?若不合理请说明理由请分析思考在摸袜子的实验中,如果用6个红色玻璃珠,另外还找了两张扑克牌,可以混在一起做实验吗?不可以,用不同的替代物混在一起,大大地改变了实验条件,所以结果是不准确的。注意:实验必须在相同的条件下进行,才能得到预期的结果;替代物的选择必须是合理、简单的。思考假设用小球模拟问题的实验过程中,用6个黑球代替3双黑袜子,用2个白球代替1双白袜子:
(1)有一次摸出了2个白球,但之后一直忘了把它们放回去,这会影响实验结果吗?有影响,如果不放回,就不是3双黑袜子和1双白袜
子的实验,而是中途变成了3双黑袜子实验,这两
种实验结果是不一样的。(2)如果不小心把颜色弄错了,用了2个黑球和
6个白球进行实验,结果会怎样?小球的颜色不影响恰好是一双的可能性大小(1)在抛一枚均匀硬币的实验中,如果没有硬币,则下列
可作为替代物的是 ( )
A.一颗均匀的骰子 B.瓶盖
C.图钉 D.两张扑克牌(1张黑桃,1张红桃)(2)不透明的袋中装有3个大小相同的小球,其中2个为白
色球,另一个为红色球,每次从袋中摸出一个球,然后放回
搅匀再摸,研究恰好摸出红色小球的机会,以下替代实验方
法不可行的是 ( )
A.用3张卡片,分别写上“白”、“红”, “红”然后反复抽取
B.用3张卡片,分别写上“白”、“白”、“红”,然后反复抽取
C.用一枚硬币,正面表示“白”,反面表示“红”,然后反复抽取
D.用一个转盘,盘面分:白、红两种颜色,其中白色盘面的面
积为红色的2倍,然后反复转动转盘
2。各种结果发生的可能性相等。 复习巩固 但在我们的身边,有很多试验的所有可能性是不相等且结果不是有限多个,这些事件的概率怎样确定呢? 提出问题 在同样条件下,通过大量反复的试验,根据一个随机事件发生的频率所逐渐稳定到的常数,可以估计这个事件发生的概率。 历史上曾有人做过抛掷硬币的大量重复试验,结果如下表 :历史上曾有人作过抛掷硬币的大量重复实验,结果如下表所示比较我们自己作的实验数据探索研究实验结论:当抛硬币的次数很多时,出现下面的频率值是
稳定的,接近于常数0.5,在它附近摆动. 当抛掷硬币的次数很多时,出现正面的频率值是稳定的,接近于常数0.5,在它附近摆动. 随机事件及其概率很多 稳定常数 随机事件在一次试验中是否
发生虽然不能事先确定,但是在
大量重复试验的情况下,它的发
生呈现出一定的规律性.出现的频率值接近于常数.随机事件及其概率某批乒乓球产品质量检查结果表: 当抽查的球数很多时,抽到优等品的频率 接近于常数0.95,在它附近摆动。 很多常数某种油菜籽在相同条件下的发芽试验结果表: 当试验的油菜籽的粒数很多时,油菜籽发芽
的频率 接近于常数0.9,在它附近摆动。很多 常数随机事件及其概率事件 的概率的定义: 一般地,在大量重复进行同一试验时,事件 发生的频率 (n为实验的次数,m是事件发生的频数)总是接近于某个常数,在它附近摆动,这时就把这个常数叫做事件 的概率,记做 . 由定义可知: (1)求一个事件的概率的基本方法是通过大量的重复试验; (3)概率是频率的稳定值,而频率是概率的近似值; (4)概率反映了随机事件发生的可能性的大小; (5)必然事件的概率为1,不可能事件的概率为0.因此 . (2)只有当频率在某个常数附近摆动时,这个常数才叫做事件A 的概率; 某林业部门要考查某种幼树在一定条件的移植成活率,应采用什么具体的做法? 答:在同样条件下,大量地对这种幼树进行移植,并统计成活情况,计算成活的频率。如果随着移植棵数n的越来越大,频率 越来越稳定于某个常数,那么这个常数就可以被当作成活率的近似值。0.9230.8830.9050.897下图是一张模拟的统计表,请补出表中的空缺所以估计幼树移植成活的概率是 。0.90556 某水果公司以2元/千克的成本新进了10000千克的柑橘,如果公司希望这些柑橘能够获利5000元,那么在出售柑橘(已去掉损坏的柑橘)时,每千克大约定价为多少元比较合适? 问题20.1030.1010.098柑橘在运输途中会有些损坏,公司必须估算出可能损坏的柑橘总数,以便将损坏的柑橘成本折算到没有损坏的柑橘的售价中。销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行了“柑橘损坏率”的统计,把获得的数据记录在下:0.100.0990.1030.0970.0970.90某种小麦播种的发芽概率约是95%,1株麦芽长成麦苗的概率约是90%,一块试验田的麦苗数是8550株,该麦种的千粒质量为35千克,则播种这块试验田需麦种约 千克。概率是个准确值
频率是个估计值
通过大量的实验可以使频率趋于一个稳定的常数,用该常数估计概率
实验的次数越多越趋近于概率,因此用实验次数多的频率趋近的常数来估计概率较为精确
归纳4.表中是一个机器人做9999次“抛硬币”游戏时记录下的出现正面的频数和频率. (1)由这张频数和频率表可知,机器人抛掷完5次时,得到1次正面,正面出现的频率是20%,那么,也就是说机器人抛掷完5次时,得到______次反面,反面出现的频率是______.
480% (2)由这张频数和频率表可知,机器人抛掷完9999次时,得到______次正面,正面出现的频率是______.那么,也就是说机器人抛掷完9999次时,得到_______次反面,反面出现的频率是________.
500650.1% 499449.9% 5.给出以下结论,错误的有( )
①如果一件事发生的机会只有十万分之一,那么它就不可能发生. ②如果一件事发生的机会达到99.5%,那么它就必然发生. ③如果一件事不是不可能发生的,那么它就必然发生. ④如果一件事不是必然发生的,那么它就不可能发生.
A.1个 B.2个 C.3个 D.4个
D6.一位保险推销员对人们说:“人有可能得病,也有可能不得病,因此,得病与不得病的概率各占50%”他的说法( )
A.正确 B.不正确
C.有时正确,有时不正确
D.应由气候等条件确定
B7.某位同学一次掷出三个骰子三个全是“6”的事件是( )
A.不可能事件 B.必然事件
C.不确定事件可能性较大
D.不确定事件可能性较小
?
D9.现有3张牌,利用这3张牌:(1).从中抽一张牌,在未抽牌之前分别说出一件有关抽牌的必然事件,不可能事件,不确定事件.(2).任意抽一张牌,抽到的牌数字有几种可能?10.笼子里关着一只兔子(如图),兔子的主人决定把兔子放归大自然,将笼子所有的门都打开。兔子要先经过第一道(A,B,C),再经过第二道门(D或E)才能出去。问兔子走出笼子的路线(经过的两道门)有多少种不同的可能? 用1(或100%)来表示
必然事件发生的可能性,即概率为1;用0来表示不可能事件发生的可能性。即概率为0;必然事件发生的可能性是100%即概率为1;不可能事件发生的可能性是0;不确定事件发生的可能性是大于0而小于1的.即概率为0;即此时概率为小结1.随机事件的概念2.随机事件的概率的定义 在一定条件下可能发生也可能不发生的事件,叫做随机事件. 在大量重复进行同一试验时, 事件 发生的频率 总是接近于某个常数,在它附近摆动,这时就把这个常数叫做事件 的概率.1. 概率的获取有 和 两种。2. 本节课的事件概率无法用理论计算来解决,只能通过概率实验,用 来估算。理论计算实验估算频率2.某射手在同一条件下进行射击,结果如下表所示:(1)计算表中击中靶心的各个频率;
(2)这个射击一次,击中靶心的概率约是多少? 问题情景: 小明参加夏令营,一天夜里熄灯了,伸手不见五指,想到明天去八达岭长城天不亮就出发,想把袜子准备好,而现在又不能开灯。袋子里有尺码相同的3双黑袜子和1双白袜子,混放在一起,只能摸黑去拿出2只。同学们能否求出摸出的2只恰好是一双的可能性?同学们能否通过实验估计它们恰好是一双的可能性?如果手边没有袜子应该怎么办?
问题3一个学习小组有6名男生3名女生。老师要从小组的学生中先后随机地抽取3人参加几项测试,并且每名学生都可被重复抽取。你能设计一种实验来估计“被抽取的3人中有2名男生1名女生”的概率的吗?模拟实验下面的表中给出了一些模拟实验的方法,你觉得这些方法合理吗?若不合理请说明理由请分析下面的表中给出了一些模拟实验的方法,你觉得这些方法合理吗?若不合理请说明理由请分析思考在摸袜子的实验中,如果用6个红色玻璃珠,另外还找了两张扑克牌,可以混在一起做实验吗?不可以,用不同的替代物混在一起,大大地改变了实验条件,所以结果是不准确的。注意:实验必须在相同的条件下进行,才能得到预期的结果;替代物的选择必须是合理、简单的。思考假设用小球模拟问题的实验过程中,用6个黑球代替3双黑袜子,用2个白球代替1双白袜子:
(1)有一次摸出了2个白球,但之后一直忘了把它们放回去,这会影响实验结果吗?有影响,如果不放回,就不是3双黑袜子和1双白袜
子的实验,而是中途变成了3双黑袜子实验,这两
种实验结果是不一样的。(2)如果不小心把颜色弄错了,用了2个黑球和
6个白球进行实验,结果会怎样?小球的颜色不影响恰好是一双的可能性大小(1)在抛一枚均匀硬币的实验中,如果没有硬币,则下列
可作为替代物的是 ( )
A.一颗均匀的骰子 B.瓶盖
C.图钉 D.两张扑克牌(1张黑桃,1张红桃)(2)不透明的袋中装有3个大小相同的小球,其中2个为白
色球,另一个为红色球,每次从袋中摸出一个球,然后放回
搅匀再摸,研究恰好摸出红色小球的机会,以下替代实验方
法不可行的是 ( )
A.用3张卡片,分别写上“白”、“红”, “红”然后反复抽取
B.用3张卡片,分别写上“白”、“白”、“红”,然后反复抽取
C.用一枚硬币,正面表示“白”,反面表示“红”,然后反复抽取
D.用一个转盘,盘面分:白、红两种颜色,其中白色盘面的面
积为红色的2倍,然后反复转动转盘
同课章节目录
