福建省闽清县天儒中学(人教版)数学九年级上册课件:第22章二次函数阶段复习(31张ppt)
文档属性
| 名称 | 福建省闽清县天儒中学(人教版)数学九年级上册课件:第22章二次函数阶段复习(31张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-06 15:33:11 | ||
图片预览







文档简介
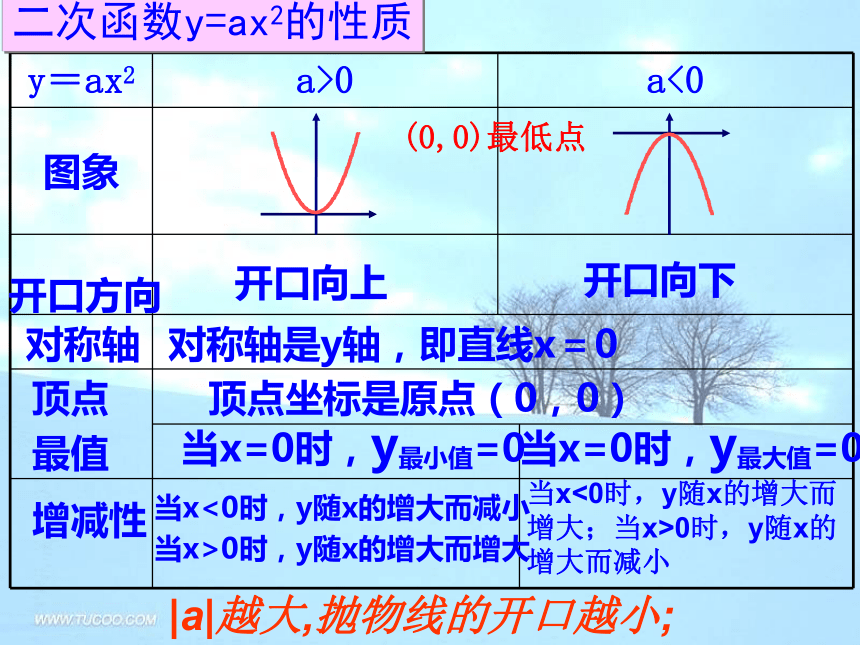
课件31张PPT。二次函数图像及性质回顾二次函数y=ax2的性质
开口方向对称轴顶点
最值增减性开口向上开口向下对称轴是y轴,即直线x=0顶点坐标是原点(0,0)当x=0时,y最小值=0当x=0时,y最大值=0当x<0时,y随x的增大而减小
当x>0时,y随x的增大而增大当x<0时,y随x的增大而
增大;当x>0时,y随x的
增大而减小(0,0)最低点|a|越大,抛物线的开口越小;1.若抛物线 的开口
向下,求n的值。2.若抛物线 上点P的坐标为
(2,-24),则抛物线上与P点对称的点
P’的坐标为 。> 0 2π 4.已知抛物线y=ax2经过点A(-2,-8)。
(1)求此抛物线的函数解析式;
(2)判断点B(-1,- 4)是否在此抛物线上。
(3)求出此抛物线上纵坐标为-6的点的坐标。解(1)把(-2,-8)代入y=ax2,得
-8=a(-2)2,解出a= -2,
所求函数解析式为 y= -2x2.(2)因为 ,所以点B(-1 ,-4)
不在此抛物线上。(3)由-6=-2x2 ,得x2=3,
所以纵坐标为-6的点有两个,
它们分别是
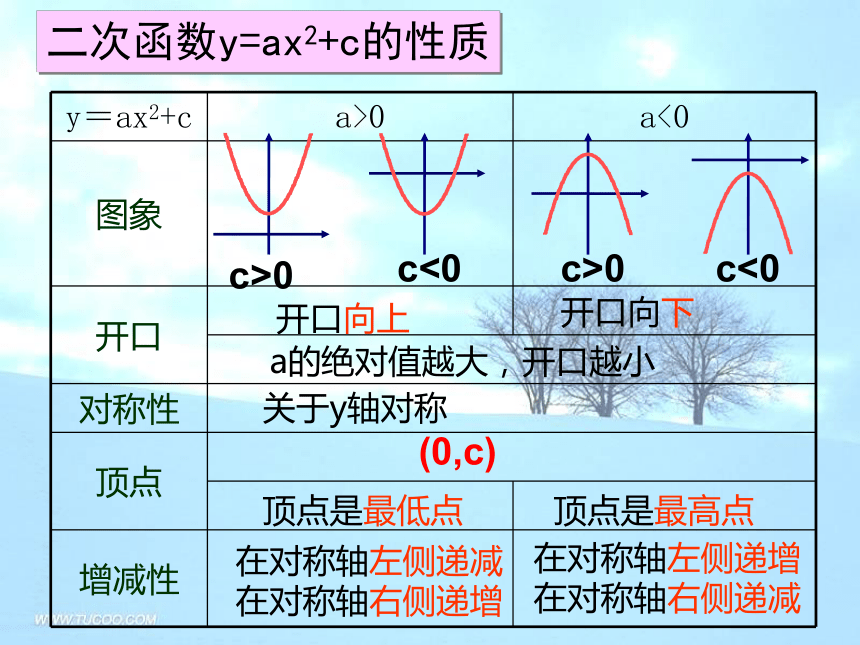
二次函数y=ax2+c的性质开口向上
开口向下
a的绝对值越大,开口越小
关于y轴对称顶点是最低点顶点是最高点在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
c>0c<0c<0c>0(0,c)
.已知抛物线的顶点是(0,-1),对称轴为y轴,且经过点
(-1,-2),则抛物线的解析式为 .
.二次函数y=mx2+m-2的图象的顶点在y轴的负半轴上,且开口向上,则m的取值范围为 .
.已知函数y=ax2+c的图象与函数y=-3x2-2的图象关于
x 轴对称,则a=____,c=____.
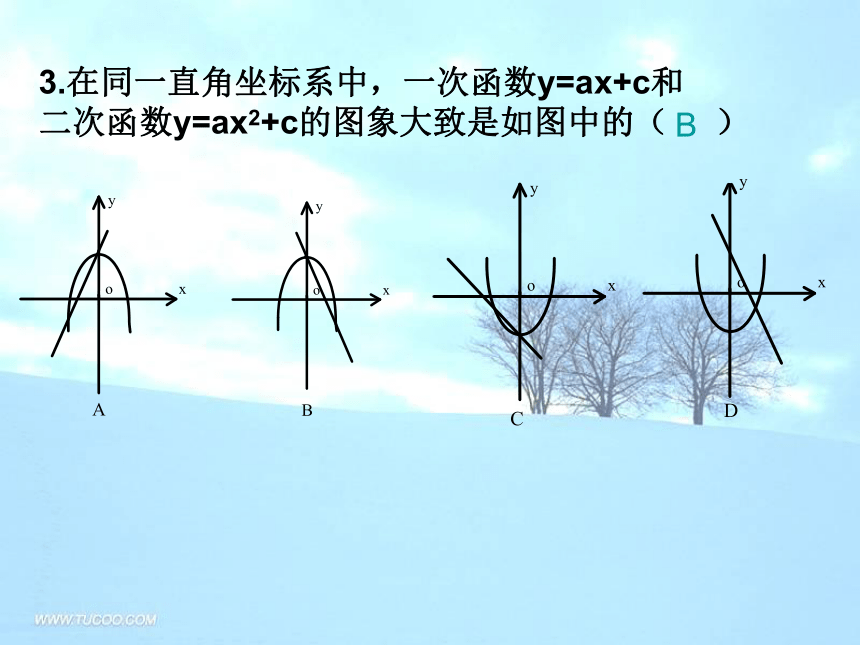
y=-x2-10<m<232知识点2 抛物线y=ax2+k的应用 BBB3.在同一直角坐标系中,一次函数y=ax+c和
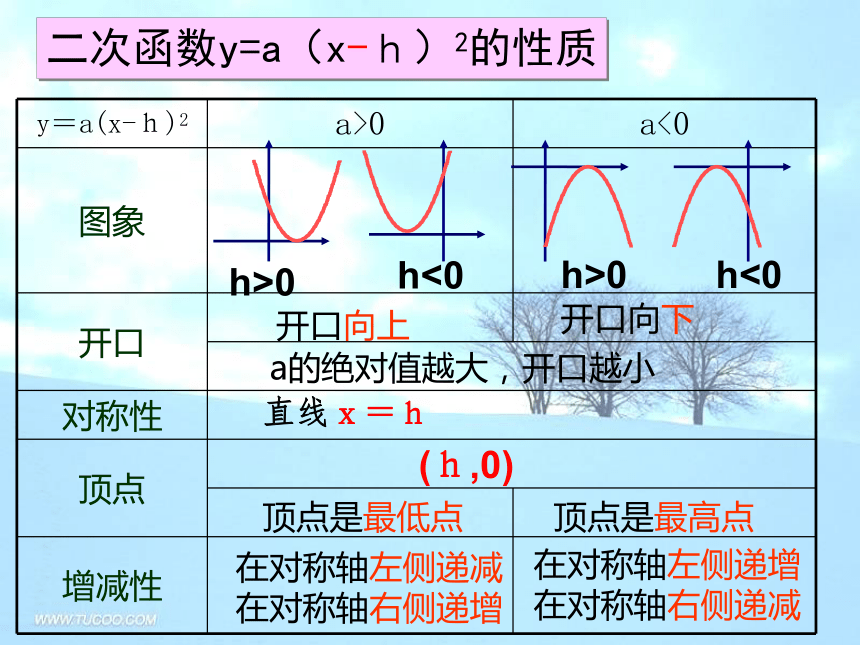
二次函数y=ax2+c的图象大致是如图中的( )B二次函数y=a(x-h)2的性质开口向上
开口向下
a的绝对值越大,开口越小
直线x=h顶点是最低点顶点是最高点在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
h>0h<0h<0h>0(h,0)知识点3.二次函数y=a(x-h)2的图象与性质B D 二次函数图像的平移 函数y=ax2 (a≠0)和函数y=ax2+c (a≠0)的图象形状 ,只是位置不同;
当c>0时,函数y=ax2+c的图象可由 y=ax2的图象向 平移 个单位得到,当c<0时,函数y=ax2+c的图象可由y=ax2的图象向 平移 个单位得到。上加下减相同上c下|c|一般地,抛物线y=a(x-h)2有如下特点:(1)对称轴是x=h;(2)顶点是(h,0).(3)抛物线y=a(x-h)2可以由抛物线y=ax2向左或向右平移|h|得到.h>0,向右平移;h<0,向左平移如何平移:1.将二次函数y=x2的图象向下平移一个单位,则平移后的二次函数的解析式为( )
A.y=x2-1 B.y=x2+1
C.y=(x-1)2 D.y=(x+1)2
2.抛物线y=ax2+c向下平移2个单位得到抛物线y=-3x2+2,则a=____,c=____.A-34A 若将抛物线y=-2(x-2)2的图象的顶点移到原点,则下列平移方法正确的是( )
A、向上平移2个单位
B、向下平移2个单位
C、向左平移2个单位
D、向右平移2个单位C4.已知y=2x2的图象是抛物线,若抛物线不动,把y轴向右平移3个单位,那么在新坐标下抛物线的解析式为( )
A.y=2(x-3)2 B.y=2x2-3
C.y=2(x+3)2 D.y=2x2+3C 例2.某涵洞是抛物线形,它的截面如图所示,现测得水面宽1.6m,涵洞顶点O到水面的距离为2.4m,在图中直角坐标系内,涵洞所在的抛物线的函数关系式是什么?
分析:
如图,以AB的垂直平分线为y轴,以过点O的y轴的垂线为x轴,建立了直角坐标系.这时,涵洞所在的抛物线的顶点在原点,对称轴是y轴,开口向下,所以可设它的函数关系式是 .此时只需抛物线上的一个点就能求出抛物线的函数关系式.AB解:如图,以AB的垂直平分线为y轴,以过点O的y轴的垂线为x轴,建立了直角坐标系。
由题意,得点B的坐标为(0.8,-2.4),
又因为点B在抛物线上,将它的坐标代入
,
得
所以
因此,函数关系式是
BA问题2
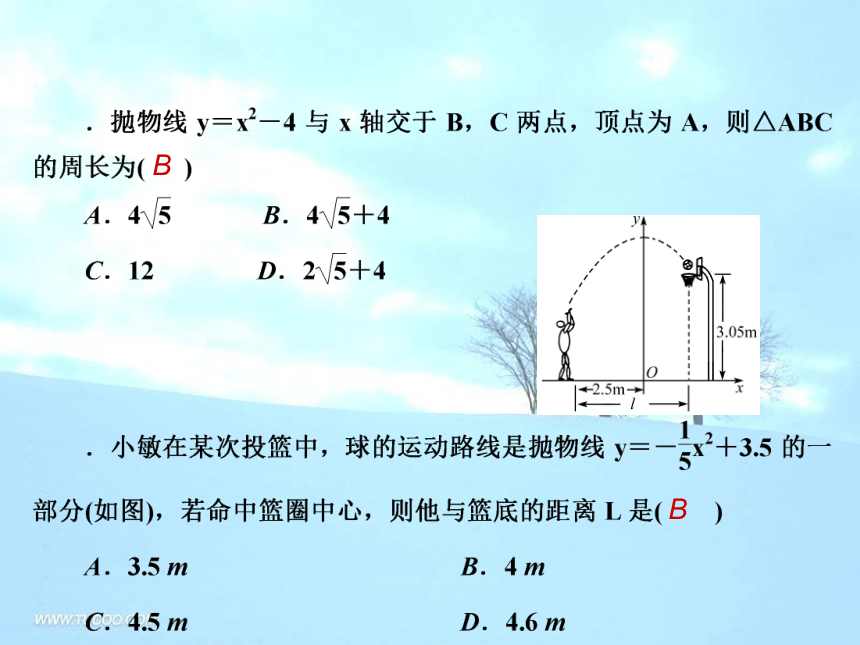
一个涵洞成抛物线形,它的截面如图,现测得,当水面宽AB=1.6 m时,涵洞顶点与水面的距离为2.4 m.这时,离开水面1.5 m处,涵洞宽ED是多少?是否会超过1 m?D (1)河北省赵县的赵州桥的桥拱是抛物线型,建立如图所示的坐标系,其函数的解析式为 y= - x2 , 当水位线在AB位置时,水面宽 AB = 30米,这时水面离桥顶的高度h是( )
A、5米 B、6米; C、8米; D、9米练习解:建立如图所示的坐标系 (2)一座抛物线型拱桥如图所示,桥下水面宽度是4m,拱高是2m.当水面下降1m后,水面的宽度是多少?(结果精确到0.1m).●A(2,-2)●B(X,-3)zxxkw (3)某工厂大门是一抛物线型水泥建筑物,如图所示,大门地面宽AB=4m,顶部C离地面高度为4.4m.现有一辆满载货物的汽车欲通过大门,货物顶部距地面2.8m,装货宽度为2.4m.请判断这辆汽车能否顺利通过大门.
某跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件)。在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面32/3米, 入水处距池边的距离为4米,同 时,运动员在距水面高度为5米 以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误。 (1)求这条抛物线的解 析式; (2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调 整好入水姿势时,距池边的水平 距离为18/5米,问此次跳水会不会失误?并通过计算说明理由。zxxkw
开口方向对称轴顶点
最值增减性开口向上开口向下对称轴是y轴,即直线x=0顶点坐标是原点(0,0)当x=0时,y最小值=0当x=0时,y最大值=0当x<0时,y随x的增大而减小
当x>0时,y随x的增大而增大当x<0时,y随x的增大而
增大;当x>0时,y随x的
增大而减小(0,0)最低点|a|越大,抛物线的开口越小;1.若抛物线 的开口
向下,求n的值。2.若抛物线 上点P的坐标为
(2,-24),则抛物线上与P点对称的点
P’的坐标为 。> 0 2π 4.已知抛物线y=ax2经过点A(-2,-8)。
(1)求此抛物线的函数解析式;
(2)判断点B(-1,- 4)是否在此抛物线上。
(3)求出此抛物线上纵坐标为-6的点的坐标。解(1)把(-2,-8)代入y=ax2,得
-8=a(-2)2,解出a= -2,
所求函数解析式为 y= -2x2.(2)因为 ,所以点B(-1 ,-4)
不在此抛物线上。(3)由-6=-2x2 ,得x2=3,
所以纵坐标为-6的点有两个,
它们分别是
二次函数y=ax2+c的性质开口向上
开口向下
a的绝对值越大,开口越小
关于y轴对称顶点是最低点顶点是最高点在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
c>0c<0c<0c>0(0,c)
.已知抛物线的顶点是(0,-1),对称轴为y轴,且经过点
(-1,-2),则抛物线的解析式为 .
.二次函数y=mx2+m-2的图象的顶点在y轴的负半轴上,且开口向上,则m的取值范围为 .
.已知函数y=ax2+c的图象与函数y=-3x2-2的图象关于
x 轴对称,则a=____,c=____.
y=-x2-10<m<232知识点2 抛物线y=ax2+k的应用 BBB3.在同一直角坐标系中,一次函数y=ax+c和
二次函数y=ax2+c的图象大致是如图中的( )B二次函数y=a(x-h)2的性质开口向上
开口向下
a的绝对值越大,开口越小
直线x=h顶点是最低点顶点是最高点在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
h>0h<0h<0h>0(h,0)知识点3.二次函数y=a(x-h)2的图象与性质B D 二次函数图像的平移 函数y=ax2 (a≠0)和函数y=ax2+c (a≠0)的图象形状 ,只是位置不同;
当c>0时,函数y=ax2+c的图象可由 y=ax2的图象向 平移 个单位得到,当c<0时,函数y=ax2+c的图象可由y=ax2的图象向 平移 个单位得到。上加下减相同上c下|c|一般地,抛物线y=a(x-h)2有如下特点:(1)对称轴是x=h;(2)顶点是(h,0).(3)抛物线y=a(x-h)2可以由抛物线y=ax2向左或向右平移|h|得到.h>0,向右平移;h<0,向左平移如何平移:1.将二次函数y=x2的图象向下平移一个单位,则平移后的二次函数的解析式为( )
A.y=x2-1 B.y=x2+1
C.y=(x-1)2 D.y=(x+1)2
2.抛物线y=ax2+c向下平移2个单位得到抛物线y=-3x2+2,则a=____,c=____.A-34A 若将抛物线y=-2(x-2)2的图象的顶点移到原点,则下列平移方法正确的是( )
A、向上平移2个单位
B、向下平移2个单位
C、向左平移2个单位
D、向右平移2个单位C4.已知y=2x2的图象是抛物线,若抛物线不动,把y轴向右平移3个单位,那么在新坐标下抛物线的解析式为( )
A.y=2(x-3)2 B.y=2x2-3
C.y=2(x+3)2 D.y=2x2+3C 例2.某涵洞是抛物线形,它的截面如图所示,现测得水面宽1.6m,涵洞顶点O到水面的距离为2.4m,在图中直角坐标系内,涵洞所在的抛物线的函数关系式是什么?
分析:
如图,以AB的垂直平分线为y轴,以过点O的y轴的垂线为x轴,建立了直角坐标系.这时,涵洞所在的抛物线的顶点在原点,对称轴是y轴,开口向下,所以可设它的函数关系式是 .此时只需抛物线上的一个点就能求出抛物线的函数关系式.AB解:如图,以AB的垂直平分线为y轴,以过点O的y轴的垂线为x轴,建立了直角坐标系。
由题意,得点B的坐标为(0.8,-2.4),
又因为点B在抛物线上,将它的坐标代入
,
得
所以
因此,函数关系式是
BA问题2
一个涵洞成抛物线形,它的截面如图,现测得,当水面宽AB=1.6 m时,涵洞顶点与水面的距离为2.4 m.这时,离开水面1.5 m处,涵洞宽ED是多少?是否会超过1 m?D (1)河北省赵县的赵州桥的桥拱是抛物线型,建立如图所示的坐标系,其函数的解析式为 y= - x2 , 当水位线在AB位置时,水面宽 AB = 30米,这时水面离桥顶的高度h是( )
A、5米 B、6米; C、8米; D、9米练习解:建立如图所示的坐标系 (2)一座抛物线型拱桥如图所示,桥下水面宽度是4m,拱高是2m.当水面下降1m后,水面的宽度是多少?(结果精确到0.1m).●A(2,-2)●B(X,-3)zxxkw (3)某工厂大门是一抛物线型水泥建筑物,如图所示,大门地面宽AB=4m,顶部C离地面高度为4.4m.现有一辆满载货物的汽车欲通过大门,货物顶部距地面2.8m,装货宽度为2.4m.请判断这辆汽车能否顺利通过大门.
某跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件)。在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面32/3米, 入水处距池边的距离为4米,同 时,运动员在距水面高度为5米 以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误。 (1)求这条抛物线的解 析式; (2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调 整好入水姿势时,距池边的水平 距离为18/5米,问此次跳水会不会失误?并通过计算说明理由。zxxkw
同课章节目录
