福建省闽清县天儒中学(人教版)数学九年级下册课件:27.1相似的图形
文档属性
| 名称 | 福建省闽清县天儒中学(人教版)数学九年级下册课件:27.1相似的图形 |  | |
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-06 15:35:20 | ||
图片预览









文档简介
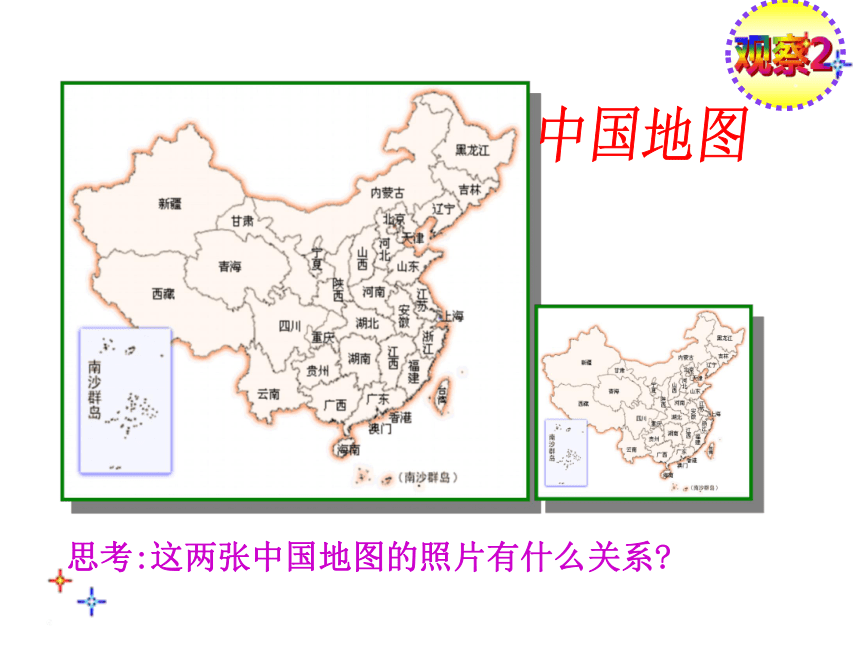
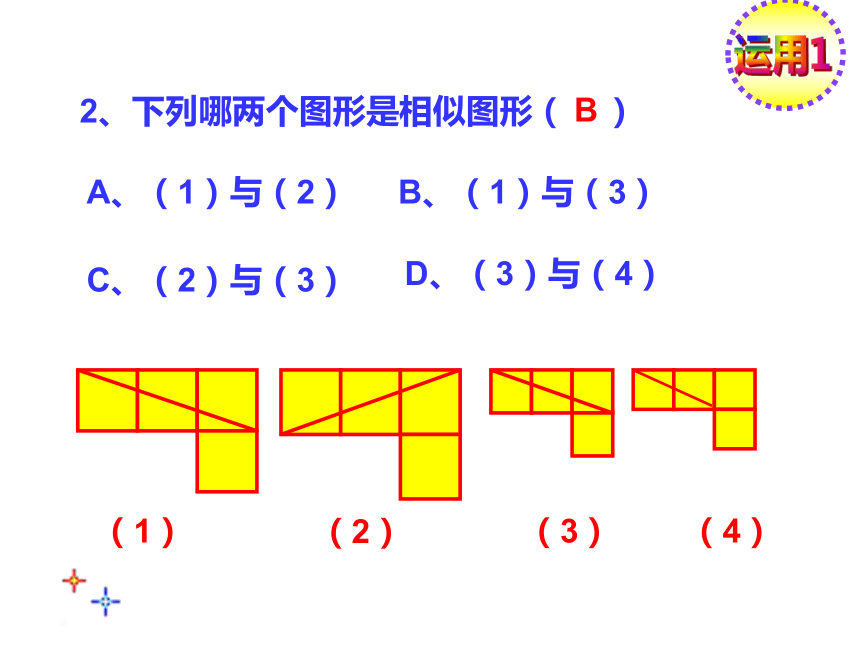
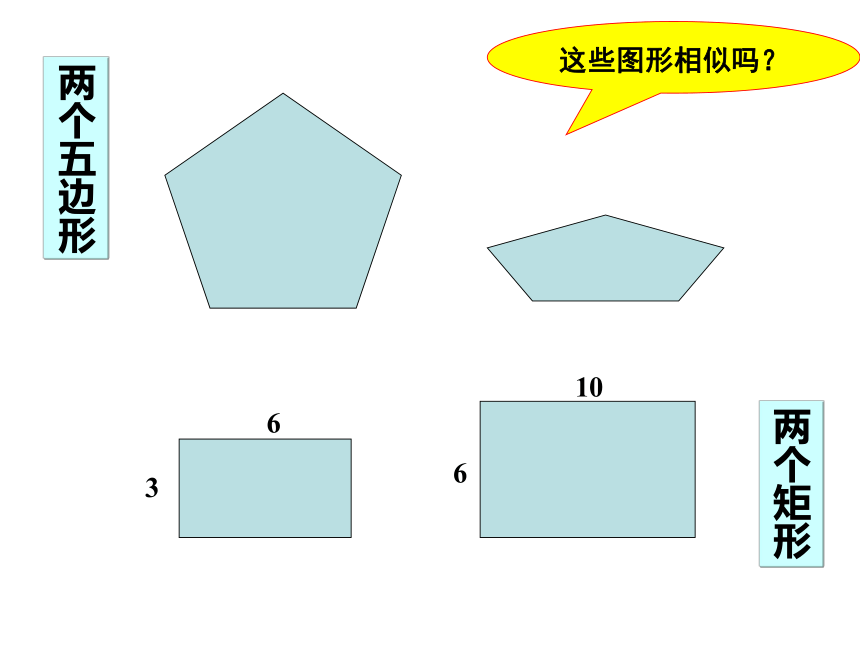
课件34张PPT。相似的图形中国地图思考:这两张中国地图的照片有什么关系?观察2想一想:我们刚才所见到的图形有什么相同和不同的地方?相同点: 不同点:形状相同.大小不同.探索1生活中我们会碰到许多这样形状相同的.大小不一定相同的图形,在数学上,我们把具有相同形状的图形称为相似图形.相似的数学符号为:∽如果两个图形形状相同,大小也相同,它们是相似形吗?相似图形:形状相同的图形相似图形定义:探索11.相似图形只针对形状,不谈大小。概念的理解:2.两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到。理解概念2、下列哪两个图形是相似图形( )BA、(1)与(2)B、(1)与(3)C、(2)与(3)D、(3)与(4)(1)(2)(3)(4)运用1这些图形相似吗?两个五边形两个矩形观察下列的图形变换后与原来的图形相似吗?你从上面的变换得到相似图形的特征吗?理解概念1.对应边的长度成比例,
2.对应角相等。相似图形的特征:如图,在下面三个矩形中,相似的是( )甲乙丙68844.56A. 甲、乙和丙 B. 甲和乙
C. 甲和丙 D. 乙和丙C 放大镜下的图形和原来的图形相似吗?理解概念思考:下图是两个三角形,它们相似吗?它们的对应角、对应边分别有什么关系?∠A= ∠A′∠B= ∠B′∠C= ∠C′两个三角形相似,它们的对应角相等,对应边成比例.相似图形:形状相同的图形图中两个四边形是相似形,仔细观察这两个图形,它们的对应边之间是否有以上的关系呢?对应角之间又有什么关系?结论:任意两个相似多边形,它们的对应角相等!对应边成比例!相似多边形的性质:相似多边形,它们的对应角相等,对应边成比例.相似多边形的判定:如果两个多边形的对应角相等,对应边成比例,那么这两个多边形相似.相似多边形对应边的比叫相似比.结论4.根据下图所示,这两个多边形相似吗?说说你的理由. 请画出左边图形的相似图形,使它们的相似比为2:1A`B`C` 把三角形ABC放大到原来的两倍(要求:放大后的顶点在格点上)。A B D F下列图形中,能确定相似的有( )A.两个半径不等的圆B.所有等边三角形C.所有等腰三角形D.所有正方形E.所有等腰梯形F.所有正六边形四边形ABCD与CDEF相似,求角 、 的大小,
和EH的长度x.解:因为四边形ABCD与EFGH相似,对应角相等;对应边成比例即解得(cm)在下面的两组图形中,各有两个相似三角形,试确定x ,y,m ,n 的值. 比例的基本性质特殊的:练习1填空题:
(1)若m是2、3、8的第四比例项,则m=_____;
(2)若x是3和7的比例中项,则x=_____。
12(3)若线段b是线段a、c的比例中项,a=3,c=7,
则b=_____。
练习2:如果那么 PA·PD=如果那么 AD·CD=PB·PC;EB·DF;练习5:如果 AC 2=AB·AD,那么 ABADACACACADAB(1)A、B两地的实际距离AB=250m,画在图上的距离A/B/=5cm,
求:图上的距离与实际距离的比;(2)一张地图的比例尺是1:30 000,甲、乙两地在这张地图上
的距离为8cm,则甲、乙两地的实际距离是______ km。1:50002.4在比例尺为1:1000000的中国地图上,量得甲、乙两地的距离为50cm,求两地的实际距离.解:设两地的实际距离为xcm两地的实际距离为60千米, 在图上量得两地的距离为20cm,这个地图的比例尺是多少?比例尺=4、在比例尺是1:8000000的“中国政区”
地图上,量得福州与上海之间的距离
是7.5cm,那么福州与上海之间的实
际距离是多少?解:设福州与上海之间的的实际距离是Xcm,
依题意得:答:福州与上海之间的的实际距离
是60千米例 题合比性质等比性质例4、已知 a:b:c=2:5:6,
求 的值.2a+5b–c
3a–2b+c解:则 a=2k,b=5k,c=6k, 市场上供应的纸张常有以下特征:每次对折后,所得的矩形和原矩形相似,问纸张的长和宽应满足什么条件?解:由矩形ABCD和矩形DEFC相似,得答:纸张的长与宽之比就为BCDAEF如图:把图中的三角形分割成4个小三角形,使它们的形状、大小完全相同,并与原三角形相似。1、如图:已知在矩形ABCD中,AB=4,AD=10,你能将它分割成两个小矩形,使它们成为相似图形吗?
2.对应角相等。相似图形的特征:如图,在下面三个矩形中,相似的是( )甲乙丙68844.56A. 甲、乙和丙 B. 甲和乙
C. 甲和丙 D. 乙和丙C 放大镜下的图形和原来的图形相似吗?理解概念思考:下图是两个三角形,它们相似吗?它们的对应角、对应边分别有什么关系?∠A= ∠A′∠B= ∠B′∠C= ∠C′两个三角形相似,它们的对应角相等,对应边成比例.相似图形:形状相同的图形图中两个四边形是相似形,仔细观察这两个图形,它们的对应边之间是否有以上的关系呢?对应角之间又有什么关系?结论:任意两个相似多边形,它们的对应角相等!对应边成比例!相似多边形的性质:相似多边形,它们的对应角相等,对应边成比例.相似多边形的判定:如果两个多边形的对应角相等,对应边成比例,那么这两个多边形相似.相似多边形对应边的比叫相似比.结论4.根据下图所示,这两个多边形相似吗?说说你的理由. 请画出左边图形的相似图形,使它们的相似比为2:1A`B`C` 把三角形ABC放大到原来的两倍(要求:放大后的顶点在格点上)。A B D F下列图形中,能确定相似的有( )A.两个半径不等的圆B.所有等边三角形C.所有等腰三角形D.所有正方形E.所有等腰梯形F.所有正六边形四边形ABCD与CDEF相似,求角 、 的大小,
和EH的长度x.解:因为四边形ABCD与EFGH相似,对应角相等;对应边成比例即解得(cm)在下面的两组图形中,各有两个相似三角形,试确定x ,y,m ,n 的值. 比例的基本性质特殊的:练习1填空题:
(1)若m是2、3、8的第四比例项,则m=_____;
(2)若x是3和7的比例中项,则x=_____。
12(3)若线段b是线段a、c的比例中项,a=3,c=7,
则b=_____。
练习2:如果那么 PA·PD=如果那么 AD·CD=PB·PC;EB·DF;练习5:如果 AC 2=AB·AD,那么 ABADACACACADAB(1)A、B两地的实际距离AB=250m,画在图上的距离A/B/=5cm,
求:图上的距离与实际距离的比;(2)一张地图的比例尺是1:30 000,甲、乙两地在这张地图上
的距离为8cm,则甲、乙两地的实际距离是______ km。1:50002.4在比例尺为1:1000000的中国地图上,量得甲、乙两地的距离为50cm,求两地的实际距离.解:设两地的实际距离为xcm两地的实际距离为60千米, 在图上量得两地的距离为20cm,这个地图的比例尺是多少?比例尺=4、在比例尺是1:8000000的“中国政区”
地图上,量得福州与上海之间的距离
是7.5cm,那么福州与上海之间的实
际距离是多少?解:设福州与上海之间的的实际距离是Xcm,
依题意得:答:福州与上海之间的的实际距离
是60千米例 题合比性质等比性质例4、已知 a:b:c=2:5:6,
求 的值.2a+5b–c
3a–2b+c解:则 a=2k,b=5k,c=6k, 市场上供应的纸张常有以下特征:每次对折后,所得的矩形和原矩形相似,问纸张的长和宽应满足什么条件?解:由矩形ABCD和矩形DEFC相似,得答:纸张的长与宽之比就为BCDAEF如图:把图中的三角形分割成4个小三角形,使它们的形状、大小完全相同,并与原三角形相似。1、如图:已知在矩形ABCD中,AB=4,AD=10,你能将它分割成两个小矩形,使它们成为相似图形吗?
