福建省闽清县天儒中学(人教版)数学九年级下册课件:27-2相似三角形的性质(共39张PPT)
文档属性
| 名称 | 福建省闽清县天儒中学(人教版)数学九年级下册课件:27-2相似三角形的性质(共39张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-06 15:35:17 | ||
图片预览







文档简介
课件39张PPT。相似三角形的性质(2)相似三角形有什么性质?相似三角形对应角 ,
相似三角形对应边 ;(1)相似三角形有哪些判定方法?温故知新想一想:它们还有哪些性质?一个三角形有三条重要线段:情景引入高、中线、角平分线如果两个三角形相似,那么这些对应线段有什么关系?ΔABC∽ΔA/B/C/,
相似比为
对应高的比 观察ΔABC∽ΔA/B/C/,
相似比为
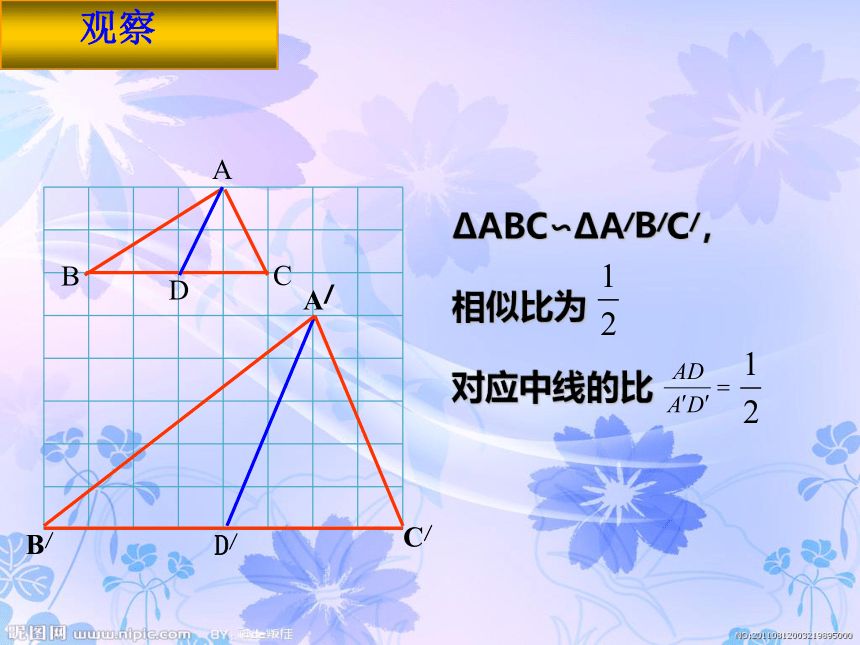
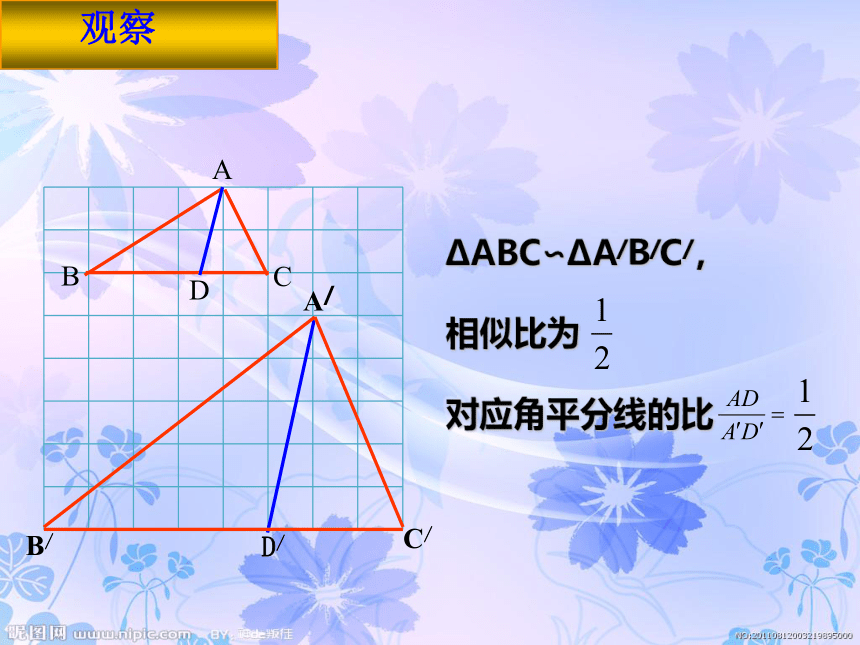
对应中线的比 观察ΔABC∽ΔA/B/C/,
相似比为
对应角平分线的比 观察可得:对应高的比
对应中线的比
对应角平分线的比小结
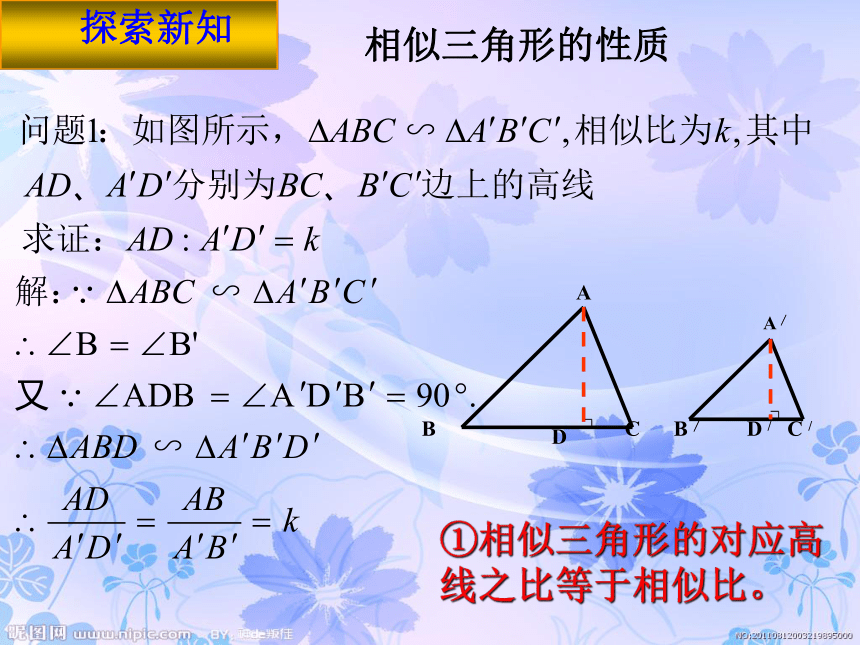
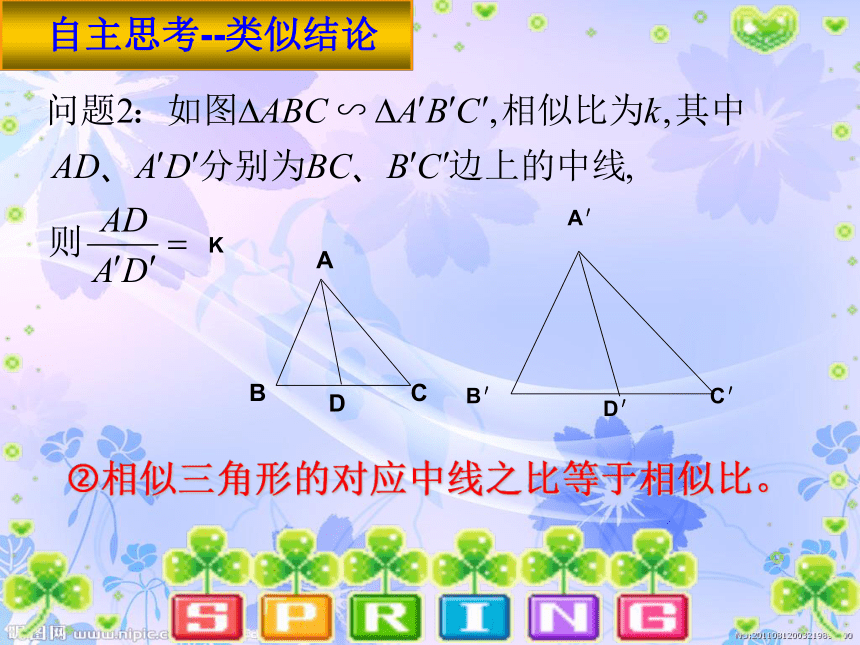
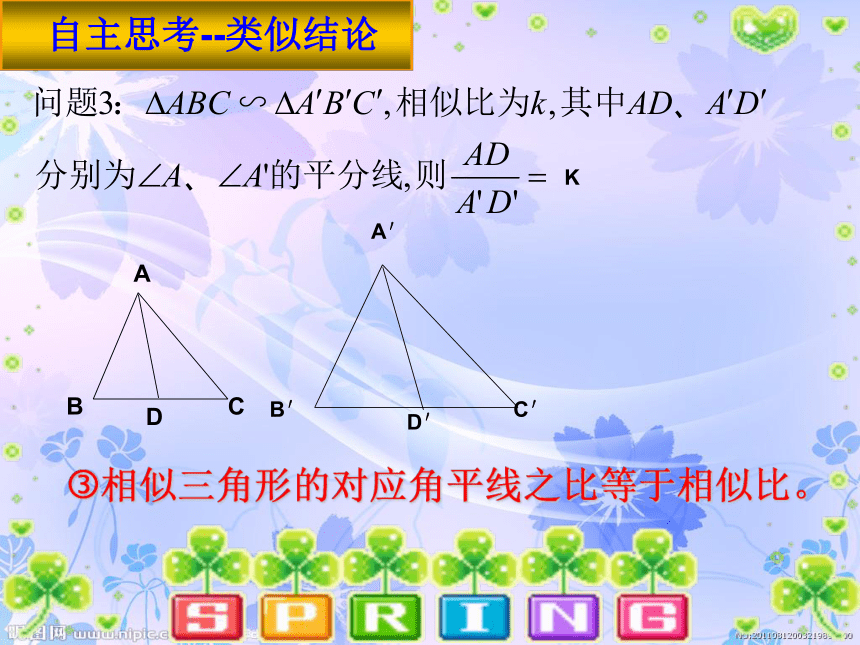
当ΔABC∽ΔA/B/C/,且相似比为 时 观察这些数据,你会有怎样的猜想呢? ①相似三角形的对应高线之比等于相似比。探索新知相似三角形的性质自主思考--类似结论?相似三角形的对应中线之比等于相似比。K自主思考--类似结论?相似三角形的对应角平线之比等于相似比。K对应高的比
对应中线的比
对应角平分线的比 相
似
三
角
形相似三角形的性质相似比=相似三角形对应线段的比等于在相似三角形中还有哪些线段的比等于相似比?相似比1、相似三角形对应边的比为2:3,那么相似比为 ,对应角的角平分线的比为 。 2、两个相似三角形相似比为1:4则对应高的比为 ,对应角的角平分线的比为 。3、两个相似三角形对应中线的比为1:4,则相似比为 ,对应高的比为 。填一填相似三角形的性质问题:两个相似三角形的周长比会等于相似比吗?如图,分别为边长为1、2、3的等边三角形,它们相似吗?(1)与(2)的相似比为 ;
(1)与(2)的周长比为 ;
(2)与(3)的相似比为 ;
(2)与(3)的周长比为 。结论:相似三角形的周长比等于 。对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形相似比.相似三角形的性质=相似三角形的性质问题:两个相似三角形的面积之间有什么关系?用心观察结论:相似三角形的面积比等于 。(1)与(2)的相似比为 ;
(1)与(2)的面积比为 ;
(2)与(3)的相似比为 ;
(2)与(3)的面积比为 。对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形相似比.相似三角形面积的=相似三角形的性质相似比的平方=如图,四边ABCD相似于四边形A/B/C/ D /,相似比为k,它们的面积比是多少?相似多边形面积的比等于相似比的平方.(1)相似三角形对应的 比等于相似比.相似三角形(多边形)的性质:(3)相似 面积的比等于相似比的平方.多边形多边形(2)相似 周长的比等于相似比.三角形三角形高线角平分线中线知 识 归 纳
(1)已知ΔABC与ΔA/B/C/ 的相似比为2:3,
则周长比为 ,对应边上中线之比 ,
面积之比为 。
(2)已知ΔABC∽ΔA/B/C/,且面积之比为9:4,
则周长之比为 ,相似比 ,对应边上的
高线之比 。 2:34:93:23: 23:22:3练 一 练例1、如图在ΔABC 和ΔDEF中,AB=2DE,AC=2DF,∠A=∠D,ΔABC的周长是24,面积是 ,求ΔDEF的周长和面积。解:在△ABC和△DEF中,∵AB=2DE,AC=2DF,
∴又∠D=∠A,
∴△DEF∽△ABC,相似比为∴△DEF的周长为×24=12面积为例 题 讲 解例2、如图,在△ABC中,D是AB的中点, DE∥BC则:(1)S △ADE : S △ABC =(2)S △ADE: S 梯形DBCE =1:41:3(1)相似三角形对应的 比等于相似比.(3)相似 面积的比等于相似比的平方.多边形多边形(2)相似 周长的比等于相似比.三角形三角形高线角平分线中线议一议:本节课你学到了什么?1、如图,FG∥BC,AE⊥FG,AD⊥BC,E、D是垂足,FG=6,BC=15,求:(1)AE:ED。提高拓展变式训练(3)若FGHI是正方形,它的边长是多少?你会把这个正方形剪出来吗?(2)若AD=10,求ED的长。1、如图,FG∥BC,AE⊥FG,AD⊥BC,E、D是垂足,FG=6,BC=15,求:(1)AE:ED。
2、如图,△ABC是一块锐角三角形余料,
边BC=120毫米,高AD=80毫米,要把它加
工成正方形零件,使正方形的一边在BC上,
其余两个顶点分别在AB、AC上,这个正方
形零件的边长是多少?解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
∵PN∥BC ∴△APN∽ △ABC
∴练一练1.如图,点E是平行四边形ABCD的边AB的延长线上一点,且AB = 4 BE ,连接DE交BC于点F.
(1)求 的值
(2)若S△BEF =2,求S?ABCD 3. 这是圆桌正上方的灯泡(当成一个点)发出的光线照射桌面形成阴影的示意图,已知桌面的直径为1.2米,桌面距离地面为1米,若灯泡距离地面3米,则地面上阴影部分的面积为多少? 4. △ABC中,DE∥BC,EF∥AB,已知△ADE和△EFC的面积分别为4和9,求△ABC的面积。相似三角形对应线段的比等于相似比相似三角形周长的比等于相似比相似三角形面积的比等于相似比的平方
相似三角形对应边 ;(1)相似三角形有哪些判定方法?温故知新想一想:它们还有哪些性质?一个三角形有三条重要线段:情景引入高、中线、角平分线如果两个三角形相似,那么这些对应线段有什么关系?ΔABC∽ΔA/B/C/,
相似比为
对应高的比 观察ΔABC∽ΔA/B/C/,
相似比为
对应中线的比 观察ΔABC∽ΔA/B/C/,
相似比为
对应角平分线的比 观察可得:对应高的比
对应中线的比
对应角平分线的比小结
当ΔABC∽ΔA/B/C/,且相似比为 时 观察这些数据,你会有怎样的猜想呢? ①相似三角形的对应高线之比等于相似比。探索新知相似三角形的性质自主思考--类似结论?相似三角形的对应中线之比等于相似比。K自主思考--类似结论?相似三角形的对应角平线之比等于相似比。K对应高的比
对应中线的比
对应角平分线的比 相
似
三
角
形相似三角形的性质相似比=相似三角形对应线段的比等于在相似三角形中还有哪些线段的比等于相似比?相似比1、相似三角形对应边的比为2:3,那么相似比为 ,对应角的角平分线的比为 。 2、两个相似三角形相似比为1:4则对应高的比为 ,对应角的角平分线的比为 。3、两个相似三角形对应中线的比为1:4,则相似比为 ,对应高的比为 。填一填相似三角形的性质问题:两个相似三角形的周长比会等于相似比吗?如图,分别为边长为1、2、3的等边三角形,它们相似吗?(1)与(2)的相似比为 ;
(1)与(2)的周长比为 ;
(2)与(3)的相似比为 ;
(2)与(3)的周长比为 。结论:相似三角形的周长比等于 。对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形相似比.相似三角形的性质=相似三角形的性质问题:两个相似三角形的面积之间有什么关系?用心观察结论:相似三角形的面积比等于 。(1)与(2)的相似比为 ;
(1)与(2)的面积比为 ;
(2)与(3)的相似比为 ;
(2)与(3)的面积比为 。对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形相似比.相似三角形面积的=相似三角形的性质相似比的平方=如图,四边ABCD相似于四边形A/B/C/ D /,相似比为k,它们的面积比是多少?相似多边形面积的比等于相似比的平方.(1)相似三角形对应的 比等于相似比.相似三角形(多边形)的性质:(3)相似 面积的比等于相似比的平方.多边形多边形(2)相似 周长的比等于相似比.三角形三角形高线角平分线中线知 识 归 纳
(1)已知ΔABC与ΔA/B/C/ 的相似比为2:3,
则周长比为 ,对应边上中线之比 ,
面积之比为 。
(2)已知ΔABC∽ΔA/B/C/,且面积之比为9:4,
则周长之比为 ,相似比 ,对应边上的
高线之比 。 2:34:93:23: 23:22:3练 一 练例1、如图在ΔABC 和ΔDEF中,AB=2DE,AC=2DF,∠A=∠D,ΔABC的周长是24,面积是 ,求ΔDEF的周长和面积。解:在△ABC和△DEF中,∵AB=2DE,AC=2DF,
∴又∠D=∠A,
∴△DEF∽△ABC,相似比为∴△DEF的周长为×24=12面积为例 题 讲 解例2、如图,在△ABC中,D是AB的中点, DE∥BC则:(1)S △ADE : S △ABC =(2)S △ADE: S 梯形DBCE =1:41:3(1)相似三角形对应的 比等于相似比.(3)相似 面积的比等于相似比的平方.多边形多边形(2)相似 周长的比等于相似比.三角形三角形高线角平分线中线议一议:本节课你学到了什么?1、如图,FG∥BC,AE⊥FG,AD⊥BC,E、D是垂足,FG=6,BC=15,求:(1)AE:ED。提高拓展变式训练(3)若FGHI是正方形,它的边长是多少?你会把这个正方形剪出来吗?(2)若AD=10,求ED的长。1、如图,FG∥BC,AE⊥FG,AD⊥BC,E、D是垂足,FG=6,BC=15,求:(1)AE:ED。
2、如图,△ABC是一块锐角三角形余料,
边BC=120毫米,高AD=80毫米,要把它加
工成正方形零件,使正方形的一边在BC上,
其余两个顶点分别在AB、AC上,这个正方
形零件的边长是多少?解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
∵PN∥BC ∴△APN∽ △ABC
∴练一练1.如图,点E是平行四边形ABCD的边AB的延长线上一点,且AB = 4 BE ,连接DE交BC于点F.
(1)求 的值
(2)若S△BEF =2,求S?ABCD 3. 这是圆桌正上方的灯泡(当成一个点)发出的光线照射桌面形成阴影的示意图,已知桌面的直径为1.2米,桌面距离地面为1米,若灯泡距离地面3米,则地面上阴影部分的面积为多少? 4. △ABC中,DE∥BC,EF∥AB,已知△ADE和△EFC的面积分别为4和9,求△ABC的面积。相似三角形对应线段的比等于相似比相似三角形周长的比等于相似比相似三角形面积的比等于相似比的平方
