福建省闽清县天儒中学(人教版)数学九年级下册课件:27-3位似(共33张PPT)
文档属性
| 名称 | 福建省闽清县天儒中学(人教版)数学九年级下册课件:27-3位似(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-06 00:00:00 | ||
图片预览





文档简介
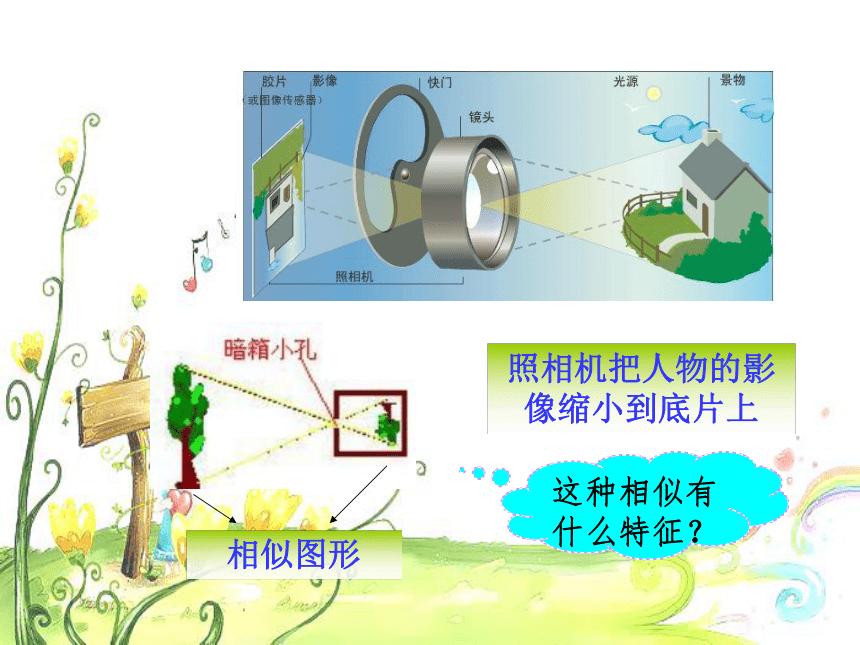
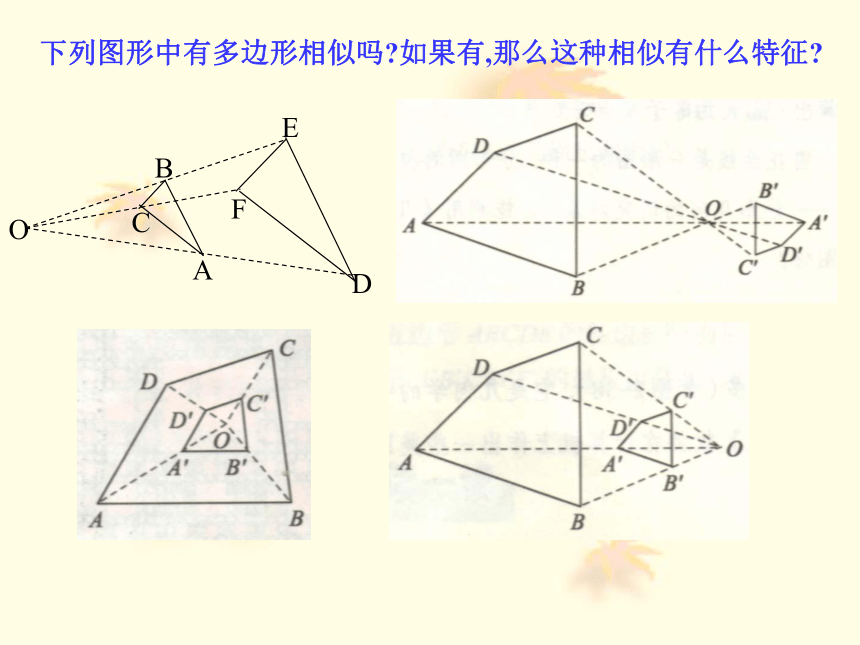
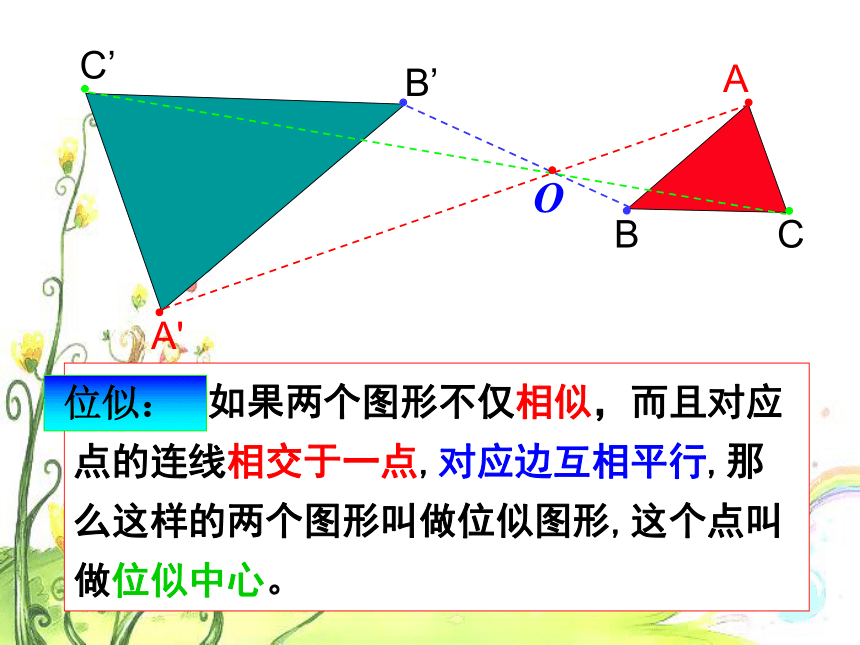
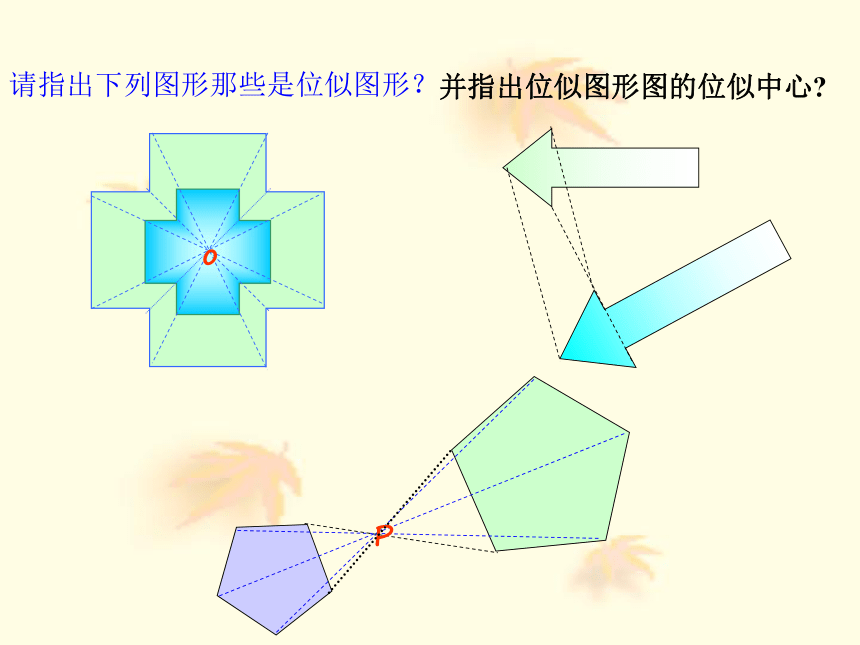
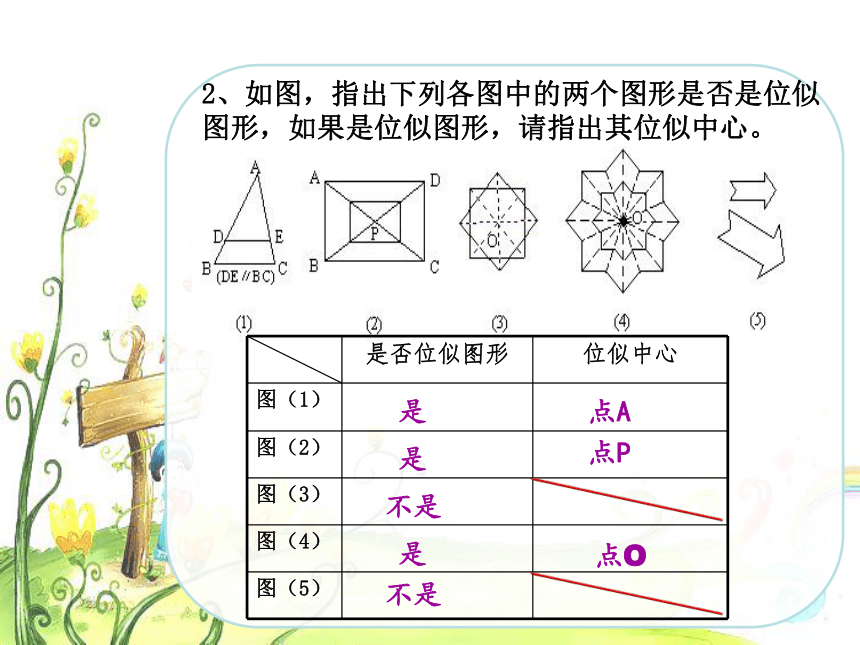
课件33张PPT。位似相似图形这种相似有什么特征?照相机把人物的影像缩小到底片上相似图形这种相似有什么特征?在幻灯机上放映幻灯片时,把幻灯片上的图象放大到屏幕上在照相馆里,摄影师通过照相机把实物的图象缩小在底片上这样放大或缩小的图形,形状_____,大小______,所以它们_____.相同不同相似放映机下列图形中有多边形相似吗?如果有,那么这种相似有什么特征? 如果两个图形不仅相似,而且对应点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心。OABA'C’B’C 位似: 请指出下列图形那些是位似图形?oP并指出位似图形图的位似中心?2、如图,指出下列各图中的两个图形是否是位似图形,如果是位似图形,请指出其位似中心。 是点A是点P不是是点O不是我们学习了在平面直角坐标系中,如何用坐标表示某些平移、轴对称、旋转(中心对称)等变换,相似也是一种图形的变换,一些特殊的相似(如位似)也可以用图形坐标的变化来表示。 位似是一种具有位置关系的相似。
位似图形是相似图形的特殊情形。
位似图形必定是相似图形,而相似图形不一定是位似图形。
两个位似图形的位似中心只有一个。
两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧。
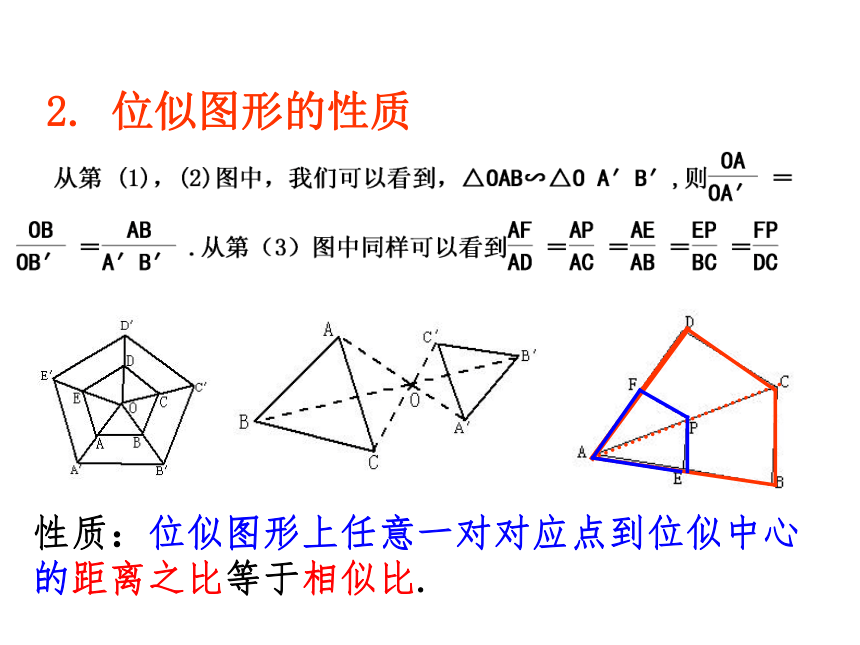
注意思考:位似图形有何性质?2. 位似图形的性质 性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比. 对应点与位似中 心共线。
不经过位似中心的对应边平行。
位似图形上任意一对应点到位似中心的距离之比等于位似比。
位似图形的性质若△ABC与△A’B’C’的相似比为:1:2,则OA:OA’=( )。OAA’BCB’C’1:2
.四边形ABCD和四边形A’B’C’D’位似,
O为位似中心,若OA:OA’=1:4,那么
S四边形ABCD:S四边形A’B’C’D’=_____。
1:16如同,△OAB和△OCD是位似图形,AB与CD平行吗?
为什么?AB∥CD∵△OAB与△ODC是位似图形∴△OAB∽△OCD∴∠OAB=∠CAB∥CDO.ABCA'C’B’. 1.如图,已知△ABC和点O.以O为位似中心,求作△ABC的位似图形,并把△ABC的边长扩大到原来的两倍. OA:OA’ =OB:OB’ =OC:OC’= 1:2思考:还有没其他作法?O.ABA'C’B’C如果位似中心跑到三角形内部呢?ACBOABA’C’B’CO以0为中心把△ABC
缩小为原来的一半。2. 分别在线段OA、OB、OC、OD上取点A'、B'、C'、D',使得 3. 顺次连接点A'、B'、C'、D',所得四边形A'B'C'D'就是所要求的图形.ODABCA'B'C'D'如何才能把四边形ABCD缩小到原来的1/2?1. 在四边形外任选一点O(如图),练一练对于上面的问题,还有其他方法吗?ODABCA'B'C'D'DABC探究B'A'C'D' ①确定位似中心,位似中心的位置可随意选择;
②确定原图形的关键点,如四边形有四个关键点,即它的四个顶点;
③确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小;
④符合要求的图形不唯一,因为所作的图形与所确定的位似中心的位置有关,并且同一个位似中心的两侧各有一个符合要求的图形。 位似变换的步骤 坐标中的位似A A′ B′ B在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.A′(2,1), B′(2,0)A〞(-2,-1),
B〞(-2,0)探
究观察对应点之间的坐标的变化,你有什么发现?A′ B′ C′ 在平面直角坐标系中, △ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2画它的位似图形.放大后对应点的坐标分别是多少?A′(4 ,6 ),
B′(4 ,2 ),
C′(12,4 )还有其他办法吗?CBA探
究观察对应点之间的坐标的变化,你有什么发现?归纳: 在平面直角坐标系中,如果位似变换是以原点为位似中心,得到的图形与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或
(-kx,-ky). 1、△ABO的定点坐标分别为A(-1,4),B(3,2),O(0,0),试将△ABO放大为△EFO,使△EFO与△ABO的相似比为2.5∶1,求点E和点F的坐标. 解:利用位似中对应点的坐标的变化规律,知E(-2.5,10),F(7.5,5).
或E(2.5,-10),F(-7.5,-5).
A′ D′ C′ B′ DC B A 例. 在平面直角坐标系中, 四边形ABCD的四个顶点的坐标分别为A(-6,6), B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2的位似图形.利用位似变换中对应点的坐标的变化规律,分别取点A′(-3,3), B′(-4,1), C′(-2,0), D′(-1,2)依次连接A′B′C′ D′,你还有其他办法吗?试试看.四边形A′B′C′ D′就是要求的四边形ABCD的位似图形ACBD1.如图表示△AOB和把它缩小后得到的△COD,求它们的相似比。A2.如图,△ABC三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以原点O为位似中心,将这个三角形放大为原来的2倍.BC我们已经学习了四种变换:平移、轴对称、旋转和相似(位似)你能说出他们之间的异同吗?学与思再见
位似图形是相似图形的特殊情形。
位似图形必定是相似图形,而相似图形不一定是位似图形。
两个位似图形的位似中心只有一个。
两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧。
注意思考:位似图形有何性质?2. 位似图形的性质 性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比. 对应点与位似中 心共线。
不经过位似中心的对应边平行。
位似图形上任意一对应点到位似中心的距离之比等于位似比。
位似图形的性质若△ABC与△A’B’C’的相似比为:1:2,则OA:OA’=( )。OAA’BCB’C’1:2
.四边形ABCD和四边形A’B’C’D’位似,
O为位似中心,若OA:OA’=1:4,那么
S四边形ABCD:S四边形A’B’C’D’=_____。
1:16如同,△OAB和△OCD是位似图形,AB与CD平行吗?
为什么?AB∥CD∵△OAB与△ODC是位似图形∴△OAB∽△OCD∴∠OAB=∠CAB∥CDO.ABCA'C’B’. 1.如图,已知△ABC和点O.以O为位似中心,求作△ABC的位似图形,并把△ABC的边长扩大到原来的两倍. OA:OA’ =OB:OB’ =OC:OC’= 1:2思考:还有没其他作法?O.ABA'C’B’C如果位似中心跑到三角形内部呢?ACBOABA’C’B’CO以0为中心把△ABC
缩小为原来的一半。2. 分别在线段OA、OB、OC、OD上取点A'、B'、C'、D',使得 3. 顺次连接点A'、B'、C'、D',所得四边形A'B'C'D'就是所要求的图形.ODABCA'B'C'D'如何才能把四边形ABCD缩小到原来的1/2?1. 在四边形外任选一点O(如图),练一练对于上面的问题,还有其他方法吗?ODABCA'B'C'D'DABC探究B'A'C'D' ①确定位似中心,位似中心的位置可随意选择;
②确定原图形的关键点,如四边形有四个关键点,即它的四个顶点;
③确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小;
④符合要求的图形不唯一,因为所作的图形与所确定的位似中心的位置有关,并且同一个位似中心的两侧各有一个符合要求的图形。 位似变换的步骤 坐标中的位似A A′ B′ B在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.A′(2,1), B′(2,0)A〞(-2,-1),
B〞(-2,0)探
究观察对应点之间的坐标的变化,你有什么发现?A′ B′ C′ 在平面直角坐标系中, △ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2画它的位似图形.放大后对应点的坐标分别是多少?A′(4 ,6 ),
B′(4 ,2 ),
C′(12,4 )还有其他办法吗?CBA探
究观察对应点之间的坐标的变化,你有什么发现?归纳: 在平面直角坐标系中,如果位似变换是以原点为位似中心,得到的图形与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或
(-kx,-ky). 1、△ABO的定点坐标分别为A(-1,4),B(3,2),O(0,0),试将△ABO放大为△EFO,使△EFO与△ABO的相似比为2.5∶1,求点E和点F的坐标. 解:利用位似中对应点的坐标的变化规律,知E(-2.5,10),F(7.5,5).
或E(2.5,-10),F(-7.5,-5).
A′ D′ C′ B′ DC B A 例. 在平面直角坐标系中, 四边形ABCD的四个顶点的坐标分别为A(-6,6), B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2的位似图形.利用位似变换中对应点的坐标的变化规律,分别取点A′(-3,3), B′(-4,1), C′(-2,0), D′(-1,2)依次连接A′B′C′ D′,你还有其他办法吗?试试看.四边形A′B′C′ D′就是要求的四边形ABCD的位似图形ACBD1.如图表示△AOB和把它缩小后得到的△COD,求它们的相似比。A2.如图,△ABC三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以原点O为位似中心,将这个三角形放大为原来的2倍.BC我们已经学习了四种变换:平移、轴对称、旋转和相似(位似)你能说出他们之间的异同吗?学与思再见
