河北省平泉县第四中学人教版九年级数学上册课件:22.3.1二次函数的实际应用
文档属性
| 名称 | 河北省平泉县第四中学人教版九年级数学上册课件:22.3.1二次函数的实际应用 |

|
|
| 格式 | zip | ||
| 文件大小 | 83.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-06 00:00:00 | ||
图片预览



文档简介
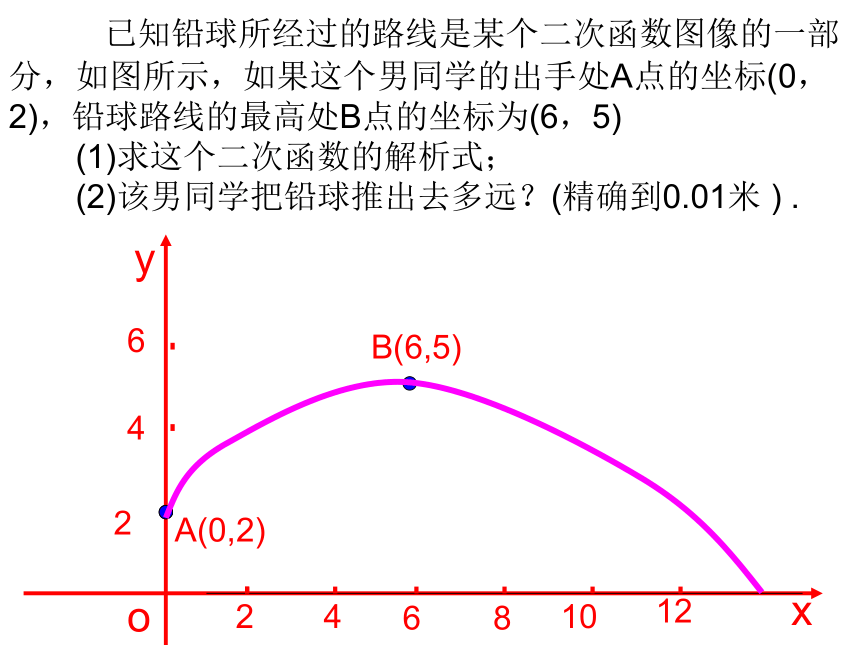
课件11张PPT。二次函数的实际应用平泉四海中学 杨秀芬例1、在体育测试时,初三的一名高个子男
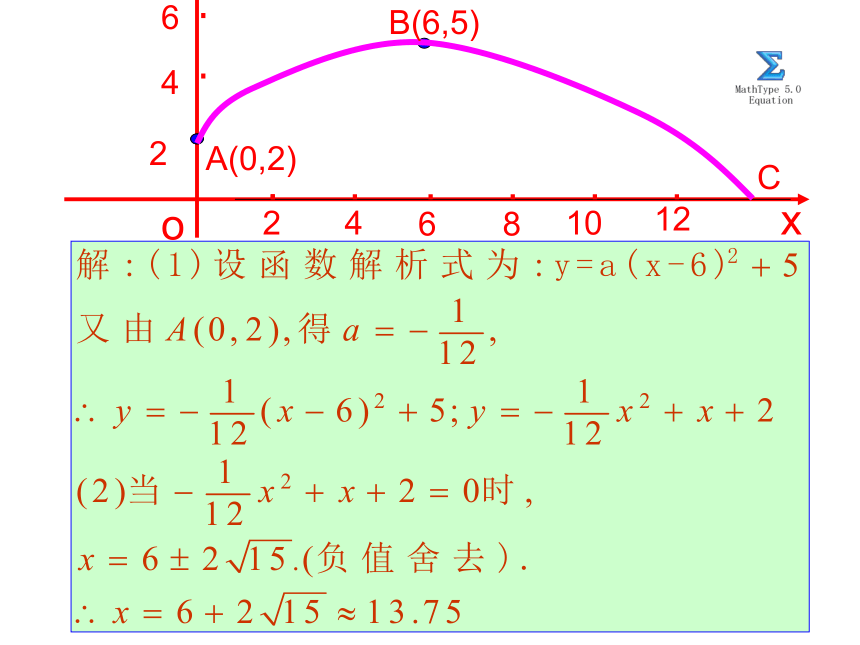
同学推铅球. 已知铅球所经过的路线是某个二次函数图像的一部分,如图所示,如果这个男同学的出手处A点的坐标(0,2),铅球路线的最高处B点的坐标为(6,5) (1)求这个二次函数的解析式; (2)该男同学把铅球推出去多远?(精确到0.01米 ) .yox24862461012B(6,5)A(0,2)C例2:
跳水运动员进行10米跳台跳水训练时,身体看成一点)在空中的运动路线是一条抛物线。 在跳某个规定动作时,正常情况下,该运动 员在空中的最高处距水面32/3米, 入水处距池边的距离为4米,同 时,运动员在距水面高度为5米 以前,必须完成规定的翻腾动作, 并调整好入水姿势,否则就会出 现失误。
(1)求这条抛物线的解析式;
(?,2/3)(2,-10)分析:(1)在给出的直角坐标系中,要确定抛物线的解析式,就要确定抛物线上三个点的坐标. 起跳点O(0,0),入水点(2,-10),最高点的纵点标为 2/3??. (0,0) ?????????????或 ??????????? 又∵抛物线对称轴在y轴右侧
所以a,b异号
故:2(2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为18/5米,问此次跳水会不会失误?并通过计算说明理由。(2)当运动员在空中距池边的水平距离为18?/5?米,即?x= ?18/5 -?2=8/5时, ????????????????????????????????????????????????
∴此时运动员距水面的高为 ?????????????????????????
因此,此次跳水会失误. 解函数应用题的步骤:设未知数(确定自变量和函数);
找等量关系,列出函数关系式;
化简,整理成标准形式等;
求自变量取值范围;
利用函数知识,求解;
写出结论。
如图,公园要建造圆形喷水池,在水池中央垂直于水面处安装一柱子OA,O恰在水面中心,A=1.25m。由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1米处达到距水面最大高度2.25米。(1)如果不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流不致落到池外?(2)若水流喷出的抛物线形状与(1)相同,水池的半径为3.5米,要使水流不落到池外,此时水流的最大高度应达到多少米?(精确到0.1米)
思考一下:
同学推铅球. 已知铅球所经过的路线是某个二次函数图像的一部分,如图所示,如果这个男同学的出手处A点的坐标(0,2),铅球路线的最高处B点的坐标为(6,5) (1)求这个二次函数的解析式; (2)该男同学把铅球推出去多远?(精确到0.01米 ) .yox24862461012B(6,5)A(0,2)C例2:
跳水运动员进行10米跳台跳水训练时,身体看成一点)在空中的运动路线是一条抛物线。 在跳某个规定动作时,正常情况下,该运动 员在空中的最高处距水面32/3米, 入水处距池边的距离为4米,同 时,运动员在距水面高度为5米 以前,必须完成规定的翻腾动作, 并调整好入水姿势,否则就会出 现失误。
(1)求这条抛物线的解析式;
(?,2/3)(2,-10)分析:(1)在给出的直角坐标系中,要确定抛物线的解析式,就要确定抛物线上三个点的坐标. 起跳点O(0,0),入水点(2,-10),最高点的纵点标为 2/3??. (0,0) ?????????????或 ??????????? 又∵抛物线对称轴在y轴右侧
所以a,b异号
故:2(2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为18/5米,问此次跳水会不会失误?并通过计算说明理由。(2)当运动员在空中距池边的水平距离为18?/5?米,即?x= ?18/5 -?2=8/5时, ????????????????????????????????????????????????
∴此时运动员距水面的高为 ?????????????????????????
因此,此次跳水会失误. 解函数应用题的步骤:设未知数(确定自变量和函数);
找等量关系,列出函数关系式;
化简,整理成标准形式等;
求自变量取值范围;
利用函数知识,求解;
写出结论。
如图,公园要建造圆形喷水池,在水池中央垂直于水面处安装一柱子OA,O恰在水面中心,A=1.25m。由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1米处达到距水面最大高度2.25米。(1)如果不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流不致落到池外?(2)若水流喷出的抛物线形状与(1)相同,水池的半径为3.5米,要使水流不落到池外,此时水流的最大高度应达到多少米?(精确到0.1米)
思考一下:
同课章节目录
