八年级数学上册试题 第2章 轴对称图形综合测试卷 --苏科版(含详解)
文档属性
| 名称 | 八年级数学上册试题 第2章 轴对称图形综合测试卷 --苏科版(含详解) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-06 18:53:42 | ||
图片预览


文档简介
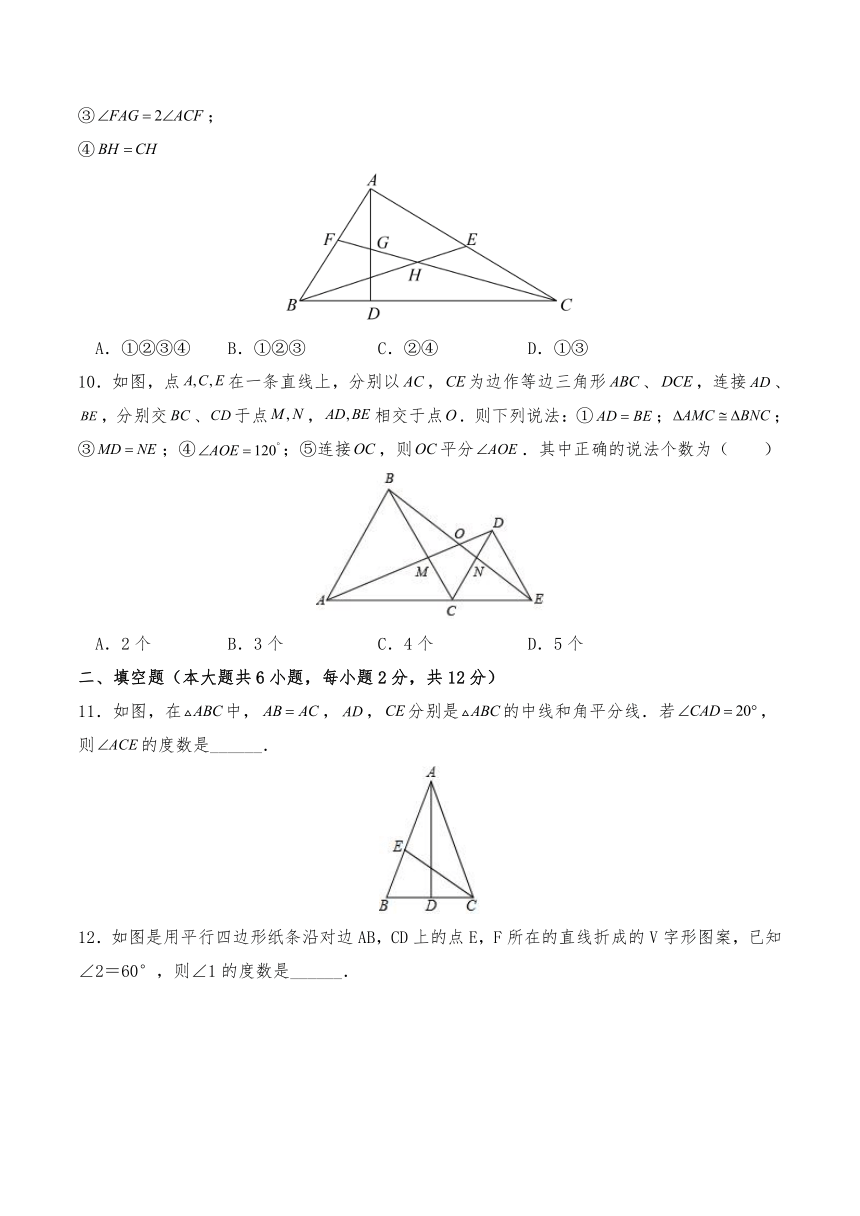
第2章《轴对称图形》综合测试卷
一、选择题(本大题共10小题,每小题2分,共20分)
1.下列图形中,不是轴对称图形的是( )
A. B. C. D.
2.如图是2×5的正方形网格,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形.则在网格中,能画出且与△ABC成轴对称的格点三角形一共有( )个.
A.1 B.2 C.3 D.4
3.如果三角形的一个外角的平分线平行于三角形的边,则这个三角形是( ).
A.锐角三角形 B.等腰三角形 C.直角三角形 D.不能确定
4.如图,在中,分别以点和点为圆心,大于的长为半径画弧,两弧相交于点,,作直线分别交,于点,下列判断错误的是( )
A. B. C. D.
5.如图,在中,,,平分交BC于点D,点E为AC的中点,连接DE,则的周长为( )
A.10 B.9 C.8 D.7
6.在中,斜边上的中线的长为,则斜边的长为( )
A. B. C. D.
7.如图,的三边AB,BC,CA长分别是20,30,40,其三条角平分线将分为三个三角形,则等于( ).
A.1∶1∶1 B.1∶2∶3 C.2∶3∶4 D.3∶4∶5
8.如图,中,,,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分;②;③的周长等于;④D是AC中点.其中正确的是( )
A.①② B.①②③ C.②③④ D.①②③④
9.如图,在中,,是高,是中线,是角平分线,交于点,交于点,下面四个说法中,其中正确的是( )
①的面积等于的面积;
②;
③;
④
A.①②③④ B.①②③ C.②④ D.①③
10.如图,点在一条直线上,分别以,为边作等边三角形、,连接、,分别交、于点,相交于点.则下列说法:①;;③;④;⑤连接,则平分.其中正确的说法个数为( )
A.2个 B.3个 C.4个 D.5个
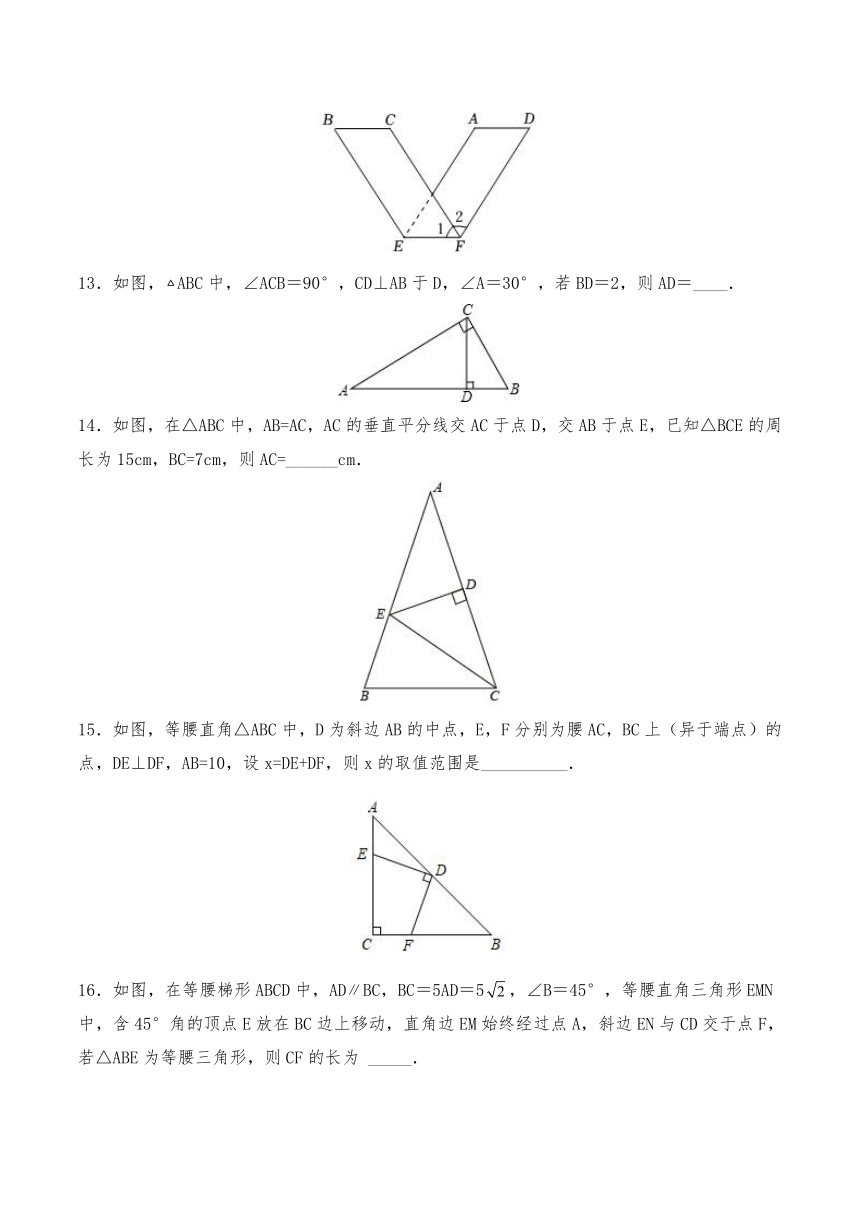
二、填空题(本大题共6小题,每小题2分,共12分)
11.如图,在中,,,分别是的中线和角平分线.若,则的度数是______.
12.如图是用平行四边形纸条沿对边AB,CD上的点E,F所在的直线折成的V字形图案,已知∠2=60°,则∠1的度数是______.
13.如图,ABC中,∠ACB=90°,CD⊥AB于D,∠A=30°,若BD=2,则AD=____.
14.如图,在△ABC中,AB=AC,AC的垂直平分线交AC于点D,交AB于点E,已知△BCE的周长为15cm,BC=7cm,则AC=______cm.
15.如图,等腰直角△ABC中,D为斜边AB的中点,E,F分别为腰AC,BC上(异于端点)的点,DE⊥DF,AB=10,设x=DE+DF,则x的取值范围是__________.
16.如图,在等腰梯形ABCD中,ADBC,BC=5AD=5,∠B=45°,等腰直角三角形EMN中,含45°角的顶点E放在BC边上移动,直角边EM始终经过点A,斜边EN与CD交于点F,若△ABE为等腰三角形,则CF的长为 _____.
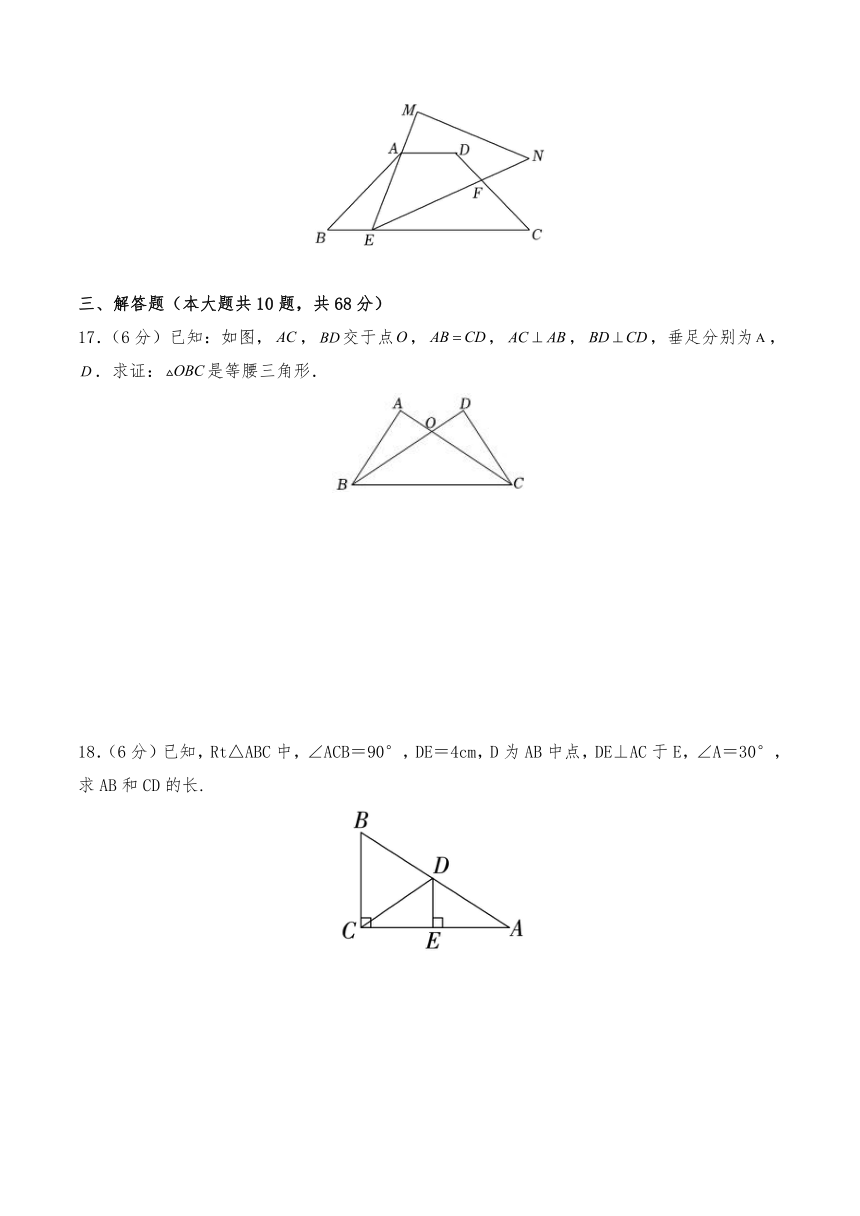
三、解答题(本大题共10题,共68分)
17.(6分)已知:如图,,交于点,,,,垂足分别为,.求证:是等腰三角形.
18.(6分)已知,Rt△ABC中,∠ACB=90°,DE=4cm,D为AB中点,DE⊥AC于E,∠A=30°,求AB和CD的长.
19.(6分)如图,公路OA与OB相交于点O,在两条公路相交内部有两个村庄E,F,现要修建一个电站,使得该电站到两条公路OA和OB的距离相等,且到两个村庄的距离相等.请你用尺规作出该电站的位置.(不写作法,保留作图痕迹,写出结论)
20.(6分)如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.求证:
(1)CF=EB;
(2)AF+EB=AE.
21.(6分)如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,DF⊥AC于点F,BD=CD.
(1)求证:DE=DF;
(2)判断△ABC的形状并证明.
22.(6分)如图,在中,,AD平分∠BAC,交BC于点D,DE⊥AB于E,点F在AC上,且.
(1)求证:;
(2)若,,求BE的长.
23.(6分)已知△ABC和△DEF为等腰三角形,AB=AC,DE=DF,∠BAC=∠EDF,点E在AB上,点F在射线AC上.
(1)如图1,若∠BAC=60°,点F与点C重合,求证:AF=AE+AD;
(2)如图2,若AD=AB,求证:AF=AE+BC.
24.(6分)在△ABC中,AB=AC,在△ABC的外部作等边△ACD,E为AC的中点,连接DE并延长交BC于点F.
(1)如图1,连接BD,若∠BAC=100°,求∠BDF的度数;
(2)如图2,∠ACB的平分线交AB于点M,交EF于点N,连接BN.若BN=DN,求证:MB=MN.
25.(10分)数学课上,老师出示了如下框中的题目:
在等边三角形中,点在上,点在的延长线上,且, 如图,试确定线段与的大小关系,并说明理由.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点为的中点时,如图1,确定线段与的大小关系.请你直接写出结论:________(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,与的大小关系是:________(填“>”,“<”或“=”)理由如下:
如图2,过点作,交于点,(请你继续完成解答过程)(3)拓展结论,设计新题
在等边三角形中,点在直线上上,点在直线上,且.若的边长为3,,求的长(请你直接写出结果).
26.(10分)如图,△ABC是等边三角形,点D、E分别是直线BC、AC上的点.
(1)如图①,当点D、E分别在线段BC、AC上时,BE与AD相交于点F,且∠AFE=60°,求证:AD=BE;
(2)如图②,当点D在CB的延长线上,点E在AC的延长线上时,CF为△ABC的高线,且BD=CE,求证:CD=2AF+CE;
(3)如图③,当点D、E分别在线段BC、AC上时,BE与AD相交于点F,且∠AFE=60°,恰好CF为△ADC的高线,BF=35,DF=5.求EF的长.
答案
一、选择题
1.C
【解析】解:A、是轴对称图形,故此选项不符合题意;
B、是轴对称图形,故此选项不符合题意;
C、不是轴对称图形,故此选项符合题意;
D、是轴对称图形,故此选项不符合题意;
故选:C.
2.D
【解析】解:如图所示:与△ABC成轴对称的格点三角形一共4个,
故选D.
3.B
【解析】解:如图,
CD平分∠ACE,且,
∴∠ACD=∠DCE,∠A=∠ACD,∠B=∠DCE,
∴∠B=∠A,
∴△ABC为等腰三角形,
故选B.
4.A
【解析】解:由作图知,直线是线段的垂直平分线,
所以、、,故C、D正确,不符合题意,
∵,
,故B正确,不符合题意,
故选:.
5.D
【解析】解:∵AB=AC,AD平分∠BAC,BC=4,
∴AD⊥BC,CD=BD=BC=2,
∵点E为AC的中点,
∴DE=CE=AC=2.5,
∴△CDE的周长=CD+DE+CE=2+2.5+2.5=7.
故选:D.
6.C
【解析】解:∵在中,斜边上的中线的长为,
∴cm.
故选:C.
7.C
【解析】解:如图,过点分别作的垂线,垂足分别为点,
由角平分线的性质定理得:,
的三边长分别是20,30,40,
,
故选:C.
8.B
【解析】解:∵AB的垂直平分线DE交AC于D,交AB于E,
∴AD=BD,
∴∠ABD=∠A=36°,
∵AB=AC,
∴∠ABC=∠C=72°,
∴∠CBD=∠ABD=36°,
即BD平分∠ABC;故①正确;
∵∠BDC=∠A+∠ABD=72°
∴∠BDC=∠C=72°,
∴BC=BD,
∴BC=BD=AD,故②正确;
∴△BDC的周长为:BC+CD+BD=BC+CD+AD=AC+BC=AB+BC;故③正确;
∵CD<BD,
∴CD<AD,
∴D不是AC中点.故④错误.
故选:A.
9.B
【解析】解:是的AC边上的中线,
,
与等底同高,
,则说法①正确;
CF是的角平分线,
,
,是高,
,
,
由对顶角相等得:,
,则说法②正确;
,是高,
,
,
又,即,
,则结论③正确;
根据已知条件不能推出,
不能推出,则说法④错误;
综上,说法正确的是①②③,
故选:B.
10.D
【解析】解:∵△ABC与△DCE是等边三角形,
∴AC=BC,∠ACB=∠DCE=60°,DC=EC,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
∴(SAS)
∴AD=BE,
故①正确;
∵,
∴∠DAC=∠EBC,
又∵∠ACB=∠BCD=60°,AC=BC,
∴,
故②正确;
∵,
∴AM=BN,
∴AD-AM=BE-BN
即DM=EN
故③正确;
∵∠DAC=∠EBC,∠AMC=∠BMD
∴∠BOM=∠ACB=60°
∴∠AOE=120°
故④正确;
如图,连接OC,过点C作CH⊥AB于点H,作CF⊥BE于点F,
∵,
∴CH=CF,
∴平分,
故⑤正确;
故选:D.
二、填空题
11.35°
【解析】解:,是的中线,
,,
∴∠BAC=40°,
,
是的角平分线,
,
故答案为:.
12.60°
【解析】解:如图,由折叠知,∠1=∠3,
∵∠2=60°,
∴∠1=∠3=(180°-60°)÷2=60°,
故答案为:60°.
13.6
【解析】解:∵∠ACB=90°,∠A=30°,
∴∠B=60°,AB=2BC,
∵CD⊥AB, ∴∠BDC=90°,
∴∠BCD=90°-60°=30°,
∴BC=2BD,
∴AB=4BD,
∵BD=2,
∴AB=2×4=8,
∴AD=AB-BD=8-2=6,
故答案为6.
14.8
【解析】解:∵AC的垂直平分线交AC于点D,交AB于点E,
∴AE=CE,
∴AB=AE+BE=CE+BE,
∵△BCE的周长=BC+BE+CE=AB+BC=15cm,BC=7cm,
∴AB=8cm,
∴AC=AB=8cm,
故答案为:8.
15.
【解析】如图所示,
过点D作DM⊥AC,DN⊥BC,分别交AC、BC于M、N,
∵△ABC是等腰三角形,点D是AB的中点,
∴DM= DN,又DE⊥DF,
∴∠EDM=∠FDN,
在△EDM和△FDN中
∴≌(ASA),
∴DE=DF,
在中, ∵AB=10,
∴AC=BC=,
当DE、DF与边垂直时和最小,即
,
当E或F有一个与C重合时,其和最大,即
,
∴.
故答案为:.
16.3或2或
【解析】解:如图,过点A作AM⊥BC于M,过点D作DN⊥BC于N,
∵等腰梯形ABCD中,AD∥BC,BC=5AD=5,
∴BM=(BC﹣AD)=,∠C=∠B=45°,
∵∠B=45°,
∴AB=BM×=4,
①如图1,AE=BE时,
∵∠B=45°,
∴∠BAE=∠B=45°,
∴△ABE是等腰直角三角形,
∴BE=AB=2,
∴CE=BC﹣BE=5﹣2=3,
又∵∠CEF=180°﹣∠AEB﹣∠AEF=180°﹣90°﹣45°=45°,
∴△CEF是等腰直角三角形,
∴CF=CE=3;
②如图2,AB=BE时,
∵∠B=45°,
∴∠AEB=(180°﹣∠B)=(180°﹣45°)=67.5°,
∴∠CEF=180°﹣∠AEB﹣∠AEF=180°﹣67.5°﹣45°=67.5°,
∴∠CFE=180°﹣∠C﹣∠CEF=180°﹣45°﹣67.5°=67.5°,
∴∠CEF=∠CFE,
∴CF=CE,
∵BC=5,AB=4,
∴CF=CE=BC﹣BE=5﹣4;
③如图3,AB=AE时,∠AEB=∠B=45°,
∴∠CEF=180°﹣∠AEB﹣∠AEF=180°﹣45°﹣45°=90°,
∴△ABE、△CEF都是等腰直角三角形,
∴BE=AB=4,
∴CE=BC﹣BE=5﹣4=,
∴CF=CE=×=2;
综上所述,CF的长为3或5﹣4或2.
故答案为:3或5﹣4或2.
三、解答题
17.证明:,,
,
在和中,
,
≌,
,
是等腰三角形.
18.解:∵DE⊥AC,∠A=30°,DE=4cm,
∴AD=2DE=8cm;
∵D为AB中点,
∴AB=2AD=16cm,
∵∠ACB=90°,
∴CD=AB=8cm.
∴AB和CD的长分别为:16cm,8cm.
19.解:电站应修建在∠AOB的角平分线和线段CD的垂直平分线的交点P处,如图所示:点P即为所求.
20.(1)证明:∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴DC=DE,
在Rt△DCF和Rt△DEB中,
,
∴Rt△DCF≌Rt△DEB(HL),
∴CF=EB;
(2)∵Rt△DCF≌Rt△DEB,
∴DC=DE,
∴Rt△DCA≌Rt△DEA(HL),
∴AC=AE,
∴AF+FC=AE,
即AF+BE=AE.
21.(1)证明:∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF;
(2)解:△ABC是等腰三角形,理由如下:
∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°,
在Rt△DEB和Rt△DFC中,
∴,
∴∠B=∠C,
∴AB=AC,
∴△ABC是等腰三角形.
22.(1)证明:∵AD平分∠BAC,DC⊥AC于C,DE⊥AB于E,
∴DC=DE,又DF=BD,
∴(HL),∴BE=CF.
(2)在和中,
∵DE=DF,AD=AD,∴,
∴AC=AE,AB=AE+BE=AC+BE,AC=AF+CF,
由(1)知CF=BE,∴AB=AF+BE+BE
即,∴.
23.(1)∵∠BAC=∠EDF=60°,
∴△ABC、△DEF为等边三角形,
∴∠BCE+∠ACE=∠DCA+∠ECA=60°,AB=AF
∴
∵BC=AC、CE=CD
∴△BCE≌△ACD(SAS),
∴AD=BE,
∵AB=AE+BE
∴AF=AE+AD;
(2)在FA上截取FM=AE,连接DM;AF,DE相交于点G
∵∠BAC=∠EDF,
∴∠AED=∠MFD,
∵AE=MF,ED=DF
∴△AED≌△MFD(SAS),
∴DA=DM=AB=AC,∠ADE=∠MDF,
∴∠ADE+∠EDM=∠MDF+∠EDM,
即∠ADM=∠EDF=∠BAC,
∵AC=DM
∴△ABC≌△DAM(SAS),
∴AM=BC,
∴AE+BC=FM+AM=AF.
即AF=AE+BC.
24.(1)解:∵△ACD是等边三角形,点E为AC的中点,
∴∠ADE=∠ADC=30°,AD=AC,
∵AB=AC,
∴AB=AD,∠BAD=∠BAC+∠CAD=160°,
∴∠ADB=10°,
∴∠BDF=∠ADE-∠ADB=30°-10°=20°;
(2)证明:连接AN,
∵CM平分∠ACB,
∴∠ACM=∠BCM=a,
∴∠ABC=∠ACB=2a,
∵DN是AC的垂直平分线,∴AN=CN,
∴∠NAC=∠NCA=a,
∴∠DAN=60°+a,
∵AB=AD,AN=AN,BN=DN,
∴△ABN≌△ADN(SSS),
∴∠ABN=∠ADN=30°,∠BAN=∠DAN=60°+a,
∴∠BAC=60°+2a,∴60°+2a+2a+2a=180°,
∴a=20°,∴∠NBC=∠ABC-∠ABN=40°-30°=10°,
∴∠MNB=∠MCB+∠NBC=30°,∴∠MNB=∠BMN,∴BM=MN.
25.(1)∵△ABC为等边三角形,点为的中点,
∴∠ABC=∠ACB=60°,CE平分∠ACB,
∴∠ECB=30°,
∵
∴∠D=∠ECB=30°,
∴∠DEB=60°-30°=30°,
∴DB=BE,
∵AE=BE,
∴AE=DB;故答案为:=
(2)理由如下:如图2,过作交于,∵是等边三角形,,,
,,即,
是等边三角形,,∴AB-AE=AC-AF,即BE=CF
,
,,
,
,,
在和中,,,BE=CF
,
,即,
(3)①如图:
当点E在直线BC下方时,以点E为圆心,EC长为半径画弧,交直线BC于点D,
过点E,作,延长AC于EF交于点F,∵,
∴∠AFE=∠ACB=60°,∠BCE=∠CEF,
∵∠A=60°,∠∠AFE=60°,
∴△AEF为等边三角形,
∵DE=CE∴∠BDE=∠BCE
∴∠BDE=∠CEF∵∠ABC=60°,∴∠DBE=60°,
在△BDE和△EFC中
∠BDE=∠CEF, ∠DBE=∠AFE,DE=CE
∴△BDE≌△EFC,∴BD=EF,
∵EF=AE=5,∴BD=5,
∴CD=5+3=8;②如图:
当点E在直线BC上方时,以点E为圆心,EC长为半径画弧,交直线BC于点D,
过点E作,延长CA,交EF于点F,∵,
∴∠EFC=∠ACB,∠FEC=∠ECD
∵∠ACB=∠B,
∴∠EFC=∠B=60°,
∵∠FAE=∠BAC=60°,
∴△AEF为等边三角形,∴EF=AE=5,
∵DE=CE,∴∠ECD=∠EDC,∴∠FEC=∠EDC,
在△BDE和△EFC中
∠BDE=∠CEF, ∠DBE=∠AFE,DE=CE
∴△BDE≌△EFC,∴BD=EF=5,
∴CD=BD-BC=5-3=2,综上:CD=8或2.
26.(1)证明:∵△ABC是等边三角形
∴AB=BC∴∠ABC=∠BAC=∠C=∠AFE=60°
∵∠AFE=∠BAF+∠ABF∠ABC=∠CBE+∠ABF
∴∠BAF+∠ABF=∠CBE+∠ABF
∵∠ABF是公共角
∴∠BAD=∠CBE在△ABD和△BCE中
∵∠BAD=∠CBE,AB=BC,∠ABD=∠BCE
∴△ABD≌BCE(ASA)∴AD=BE.
(2)证明:∵△ABC是等边三角形,
∴AC=BC,∠BAC=60°
∵CF为△ABC的高线
∴CF⊥AB
∴∠AFC=90°
∴∠ACF=90°-∠BAC=30°
∴AC=BC=2AF
∵BD=CE
∴CD=BC+BD=2AF+CE.
(3)解:如图,延长BE至H,使AF=FH,连接AH和CH.
∵∠AFE=60°
∴△AFH是等边三角形
∴AF=AH,∠BAC=∠FAH=60°
∴∠BAC-∠CAD=∠FAH-∠CAD
又∵∠CAD为公共边
∴∠BAF=∠CAH
在△BAF和△CAH中
∵AB=AC,∠BAF=∠CAH,AF=AH
∴△BAF≌△CAH(SAS)
∴∠ABF=∠ACH,BF=CH.
由(1)知∠ABC=∠BAC=60°,∠BAD=∠CBE
∴∠BAC-∠BAF=∠ABC-∠CBE,即∠ABF=∠CAD=∠ACH
∴AF∥CH.∠AFC+∠FCH=180°
∵CF为△ABC的高线
∴CF⊥AB
∴∠AFC=90°
∴∠FCH=90°
又∵∠AFE=60°
∴∠CFH=30°
∴AF=FH=2CH=2BF=6
∴AD=AF+DF=7由(1)知AD=BE=7
∴EF=BE-BF=7-3=4.
一、选择题(本大题共10小题,每小题2分,共20分)
1.下列图形中,不是轴对称图形的是( )
A. B. C. D.
2.如图是2×5的正方形网格,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形.则在网格中,能画出且与△ABC成轴对称的格点三角形一共有( )个.
A.1 B.2 C.3 D.4
3.如果三角形的一个外角的平分线平行于三角形的边,则这个三角形是( ).
A.锐角三角形 B.等腰三角形 C.直角三角形 D.不能确定
4.如图,在中,分别以点和点为圆心,大于的长为半径画弧,两弧相交于点,,作直线分别交,于点,下列判断错误的是( )
A. B. C. D.
5.如图,在中,,,平分交BC于点D,点E为AC的中点,连接DE,则的周长为( )
A.10 B.9 C.8 D.7
6.在中,斜边上的中线的长为,则斜边的长为( )
A. B. C. D.
7.如图,的三边AB,BC,CA长分别是20,30,40,其三条角平分线将分为三个三角形,则等于( ).
A.1∶1∶1 B.1∶2∶3 C.2∶3∶4 D.3∶4∶5
8.如图,中,,,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分;②;③的周长等于;④D是AC中点.其中正确的是( )
A.①② B.①②③ C.②③④ D.①②③④
9.如图,在中,,是高,是中线,是角平分线,交于点,交于点,下面四个说法中,其中正确的是( )
①的面积等于的面积;
②;
③;
④
A.①②③④ B.①②③ C.②④ D.①③
10.如图,点在一条直线上,分别以,为边作等边三角形、,连接、,分别交、于点,相交于点.则下列说法:①;;③;④;⑤连接,则平分.其中正确的说法个数为( )
A.2个 B.3个 C.4个 D.5个
二、填空题(本大题共6小题,每小题2分,共12分)
11.如图,在中,,,分别是的中线和角平分线.若,则的度数是______.
12.如图是用平行四边形纸条沿对边AB,CD上的点E,F所在的直线折成的V字形图案,已知∠2=60°,则∠1的度数是______.
13.如图,ABC中,∠ACB=90°,CD⊥AB于D,∠A=30°,若BD=2,则AD=____.
14.如图,在△ABC中,AB=AC,AC的垂直平分线交AC于点D,交AB于点E,已知△BCE的周长为15cm,BC=7cm,则AC=______cm.
15.如图,等腰直角△ABC中,D为斜边AB的中点,E,F分别为腰AC,BC上(异于端点)的点,DE⊥DF,AB=10,设x=DE+DF,则x的取值范围是__________.
16.如图,在等腰梯形ABCD中,ADBC,BC=5AD=5,∠B=45°,等腰直角三角形EMN中,含45°角的顶点E放在BC边上移动,直角边EM始终经过点A,斜边EN与CD交于点F,若△ABE为等腰三角形,则CF的长为 _____.
三、解答题(本大题共10题,共68分)
17.(6分)已知:如图,,交于点,,,,垂足分别为,.求证:是等腰三角形.
18.(6分)已知,Rt△ABC中,∠ACB=90°,DE=4cm,D为AB中点,DE⊥AC于E,∠A=30°,求AB和CD的长.
19.(6分)如图,公路OA与OB相交于点O,在两条公路相交内部有两个村庄E,F,现要修建一个电站,使得该电站到两条公路OA和OB的距离相等,且到两个村庄的距离相等.请你用尺规作出该电站的位置.(不写作法,保留作图痕迹,写出结论)
20.(6分)如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.求证:
(1)CF=EB;
(2)AF+EB=AE.
21.(6分)如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,DF⊥AC于点F,BD=CD.
(1)求证:DE=DF;
(2)判断△ABC的形状并证明.
22.(6分)如图,在中,,AD平分∠BAC,交BC于点D,DE⊥AB于E,点F在AC上,且.
(1)求证:;
(2)若,,求BE的长.
23.(6分)已知△ABC和△DEF为等腰三角形,AB=AC,DE=DF,∠BAC=∠EDF,点E在AB上,点F在射线AC上.
(1)如图1,若∠BAC=60°,点F与点C重合,求证:AF=AE+AD;
(2)如图2,若AD=AB,求证:AF=AE+BC.
24.(6分)在△ABC中,AB=AC,在△ABC的外部作等边△ACD,E为AC的中点,连接DE并延长交BC于点F.
(1)如图1,连接BD,若∠BAC=100°,求∠BDF的度数;
(2)如图2,∠ACB的平分线交AB于点M,交EF于点N,连接BN.若BN=DN,求证:MB=MN.
25.(10分)数学课上,老师出示了如下框中的题目:
在等边三角形中,点在上,点在的延长线上,且, 如图,试确定线段与的大小关系,并说明理由.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点为的中点时,如图1,确定线段与的大小关系.请你直接写出结论:________(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,与的大小关系是:________(填“>”,“<”或“=”)理由如下:
如图2,过点作,交于点,(请你继续完成解答过程)(3)拓展结论,设计新题
在等边三角形中,点在直线上上,点在直线上,且.若的边长为3,,求的长(请你直接写出结果).
26.(10分)如图,△ABC是等边三角形,点D、E分别是直线BC、AC上的点.
(1)如图①,当点D、E分别在线段BC、AC上时,BE与AD相交于点F,且∠AFE=60°,求证:AD=BE;
(2)如图②,当点D在CB的延长线上,点E在AC的延长线上时,CF为△ABC的高线,且BD=CE,求证:CD=2AF+CE;
(3)如图③,当点D、E分别在线段BC、AC上时,BE与AD相交于点F,且∠AFE=60°,恰好CF为△ADC的高线,BF=35,DF=5.求EF的长.
答案
一、选择题
1.C
【解析】解:A、是轴对称图形,故此选项不符合题意;
B、是轴对称图形,故此选项不符合题意;
C、不是轴对称图形,故此选项符合题意;
D、是轴对称图形,故此选项不符合题意;
故选:C.
2.D
【解析】解:如图所示:与△ABC成轴对称的格点三角形一共4个,
故选D.
3.B
【解析】解:如图,
CD平分∠ACE,且,
∴∠ACD=∠DCE,∠A=∠ACD,∠B=∠DCE,
∴∠B=∠A,
∴△ABC为等腰三角形,
故选B.
4.A
【解析】解:由作图知,直线是线段的垂直平分线,
所以、、,故C、D正确,不符合题意,
∵,
,故B正确,不符合题意,
故选:.
5.D
【解析】解:∵AB=AC,AD平分∠BAC,BC=4,
∴AD⊥BC,CD=BD=BC=2,
∵点E为AC的中点,
∴DE=CE=AC=2.5,
∴△CDE的周长=CD+DE+CE=2+2.5+2.5=7.
故选:D.
6.C
【解析】解:∵在中,斜边上的中线的长为,
∴cm.
故选:C.
7.C
【解析】解:如图,过点分别作的垂线,垂足分别为点,
由角平分线的性质定理得:,
的三边长分别是20,30,40,
,
故选:C.
8.B
【解析】解:∵AB的垂直平分线DE交AC于D,交AB于E,
∴AD=BD,
∴∠ABD=∠A=36°,
∵AB=AC,
∴∠ABC=∠C=72°,
∴∠CBD=∠ABD=36°,
即BD平分∠ABC;故①正确;
∵∠BDC=∠A+∠ABD=72°
∴∠BDC=∠C=72°,
∴BC=BD,
∴BC=BD=AD,故②正确;
∴△BDC的周长为:BC+CD+BD=BC+CD+AD=AC+BC=AB+BC;故③正确;
∵CD<BD,
∴CD<AD,
∴D不是AC中点.故④错误.
故选:A.
9.B
【解析】解:是的AC边上的中线,
,
与等底同高,
,则说法①正确;
CF是的角平分线,
,
,是高,
,
,
由对顶角相等得:,
,则说法②正确;
,是高,
,
,
又,即,
,则结论③正确;
根据已知条件不能推出,
不能推出,则说法④错误;
综上,说法正确的是①②③,
故选:B.
10.D
【解析】解:∵△ABC与△DCE是等边三角形,
∴AC=BC,∠ACB=∠DCE=60°,DC=EC,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
∴(SAS)
∴AD=BE,
故①正确;
∵,
∴∠DAC=∠EBC,
又∵∠ACB=∠BCD=60°,AC=BC,
∴,
故②正确;
∵,
∴AM=BN,
∴AD-AM=BE-BN
即DM=EN
故③正确;
∵∠DAC=∠EBC,∠AMC=∠BMD
∴∠BOM=∠ACB=60°
∴∠AOE=120°
故④正确;
如图,连接OC,过点C作CH⊥AB于点H,作CF⊥BE于点F,
∵,
∴CH=CF,
∴平分,
故⑤正确;
故选:D.
二、填空题
11.35°
【解析】解:,是的中线,
,,
∴∠BAC=40°,
,
是的角平分线,
,
故答案为:.
12.60°
【解析】解:如图,由折叠知,∠1=∠3,
∵∠2=60°,
∴∠1=∠3=(180°-60°)÷2=60°,
故答案为:60°.
13.6
【解析】解:∵∠ACB=90°,∠A=30°,
∴∠B=60°,AB=2BC,
∵CD⊥AB, ∴∠BDC=90°,
∴∠BCD=90°-60°=30°,
∴BC=2BD,
∴AB=4BD,
∵BD=2,
∴AB=2×4=8,
∴AD=AB-BD=8-2=6,
故答案为6.
14.8
【解析】解:∵AC的垂直平分线交AC于点D,交AB于点E,
∴AE=CE,
∴AB=AE+BE=CE+BE,
∵△BCE的周长=BC+BE+CE=AB+BC=15cm,BC=7cm,
∴AB=8cm,
∴AC=AB=8cm,
故答案为:8.
15.
【解析】如图所示,
过点D作DM⊥AC,DN⊥BC,分别交AC、BC于M、N,
∵△ABC是等腰三角形,点D是AB的中点,
∴DM= DN,又DE⊥DF,
∴∠EDM=∠FDN,
在△EDM和△FDN中
∴≌(ASA),
∴DE=DF,
在中, ∵AB=10,
∴AC=BC=,
当DE、DF与边垂直时和最小,即
,
当E或F有一个与C重合时,其和最大,即
,
∴.
故答案为:.
16.3或2或
【解析】解:如图,过点A作AM⊥BC于M,过点D作DN⊥BC于N,
∵等腰梯形ABCD中,AD∥BC,BC=5AD=5,
∴BM=(BC﹣AD)=,∠C=∠B=45°,
∵∠B=45°,
∴AB=BM×=4,
①如图1,AE=BE时,
∵∠B=45°,
∴∠BAE=∠B=45°,
∴△ABE是等腰直角三角形,
∴BE=AB=2,
∴CE=BC﹣BE=5﹣2=3,
又∵∠CEF=180°﹣∠AEB﹣∠AEF=180°﹣90°﹣45°=45°,
∴△CEF是等腰直角三角形,
∴CF=CE=3;
②如图2,AB=BE时,
∵∠B=45°,
∴∠AEB=(180°﹣∠B)=(180°﹣45°)=67.5°,
∴∠CEF=180°﹣∠AEB﹣∠AEF=180°﹣67.5°﹣45°=67.5°,
∴∠CFE=180°﹣∠C﹣∠CEF=180°﹣45°﹣67.5°=67.5°,
∴∠CEF=∠CFE,
∴CF=CE,
∵BC=5,AB=4,
∴CF=CE=BC﹣BE=5﹣4;
③如图3,AB=AE时,∠AEB=∠B=45°,
∴∠CEF=180°﹣∠AEB﹣∠AEF=180°﹣45°﹣45°=90°,
∴△ABE、△CEF都是等腰直角三角形,
∴BE=AB=4,
∴CE=BC﹣BE=5﹣4=,
∴CF=CE=×=2;
综上所述,CF的长为3或5﹣4或2.
故答案为:3或5﹣4或2.
三、解答题
17.证明:,,
,
在和中,
,
≌,
,
是等腰三角形.
18.解:∵DE⊥AC,∠A=30°,DE=4cm,
∴AD=2DE=8cm;
∵D为AB中点,
∴AB=2AD=16cm,
∵∠ACB=90°,
∴CD=AB=8cm.
∴AB和CD的长分别为:16cm,8cm.
19.解:电站应修建在∠AOB的角平分线和线段CD的垂直平分线的交点P处,如图所示:点P即为所求.
20.(1)证明:∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴DC=DE,
在Rt△DCF和Rt△DEB中,
,
∴Rt△DCF≌Rt△DEB(HL),
∴CF=EB;
(2)∵Rt△DCF≌Rt△DEB,
∴DC=DE,
∴Rt△DCA≌Rt△DEA(HL),
∴AC=AE,
∴AF+FC=AE,
即AF+BE=AE.
21.(1)证明:∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF;
(2)解:△ABC是等腰三角形,理由如下:
∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°,
在Rt△DEB和Rt△DFC中,
∴,
∴∠B=∠C,
∴AB=AC,
∴△ABC是等腰三角形.
22.(1)证明:∵AD平分∠BAC,DC⊥AC于C,DE⊥AB于E,
∴DC=DE,又DF=BD,
∴(HL),∴BE=CF.
(2)在和中,
∵DE=DF,AD=AD,∴,
∴AC=AE,AB=AE+BE=AC+BE,AC=AF+CF,
由(1)知CF=BE,∴AB=AF+BE+BE
即,∴.
23.(1)∵∠BAC=∠EDF=60°,
∴△ABC、△DEF为等边三角形,
∴∠BCE+∠ACE=∠DCA+∠ECA=60°,AB=AF
∴
∵BC=AC、CE=CD
∴△BCE≌△ACD(SAS),
∴AD=BE,
∵AB=AE+BE
∴AF=AE+AD;
(2)在FA上截取FM=AE,连接DM;AF,DE相交于点G
∵∠BAC=∠EDF,
∴∠AED=∠MFD,
∵AE=MF,ED=DF
∴△AED≌△MFD(SAS),
∴DA=DM=AB=AC,∠ADE=∠MDF,
∴∠ADE+∠EDM=∠MDF+∠EDM,
即∠ADM=∠EDF=∠BAC,
∵AC=DM
∴△ABC≌△DAM(SAS),
∴AM=BC,
∴AE+BC=FM+AM=AF.
即AF=AE+BC.
24.(1)解:∵△ACD是等边三角形,点E为AC的中点,
∴∠ADE=∠ADC=30°,AD=AC,
∵AB=AC,
∴AB=AD,∠BAD=∠BAC+∠CAD=160°,
∴∠ADB=10°,
∴∠BDF=∠ADE-∠ADB=30°-10°=20°;
(2)证明:连接AN,
∵CM平分∠ACB,
∴∠ACM=∠BCM=a,
∴∠ABC=∠ACB=2a,
∵DN是AC的垂直平分线,∴AN=CN,
∴∠NAC=∠NCA=a,
∴∠DAN=60°+a,
∵AB=AD,AN=AN,BN=DN,
∴△ABN≌△ADN(SSS),
∴∠ABN=∠ADN=30°,∠BAN=∠DAN=60°+a,
∴∠BAC=60°+2a,∴60°+2a+2a+2a=180°,
∴a=20°,∴∠NBC=∠ABC-∠ABN=40°-30°=10°,
∴∠MNB=∠MCB+∠NBC=30°,∴∠MNB=∠BMN,∴BM=MN.
25.(1)∵△ABC为等边三角形,点为的中点,
∴∠ABC=∠ACB=60°,CE平分∠ACB,
∴∠ECB=30°,
∵
∴∠D=∠ECB=30°,
∴∠DEB=60°-30°=30°,
∴DB=BE,
∵AE=BE,
∴AE=DB;故答案为:=
(2)理由如下:如图2,过作交于,∵是等边三角形,,,
,,即,
是等边三角形,,∴AB-AE=AC-AF,即BE=CF
,
,,
,
,,
在和中,,,BE=CF
,
,即,
(3)①如图:
当点E在直线BC下方时,以点E为圆心,EC长为半径画弧,交直线BC于点D,
过点E,作,延长AC于EF交于点F,∵,
∴∠AFE=∠ACB=60°,∠BCE=∠CEF,
∵∠A=60°,∠∠AFE=60°,
∴△AEF为等边三角形,
∵DE=CE∴∠BDE=∠BCE
∴∠BDE=∠CEF∵∠ABC=60°,∴∠DBE=60°,
在△BDE和△EFC中
∠BDE=∠CEF, ∠DBE=∠AFE,DE=CE
∴△BDE≌△EFC,∴BD=EF,
∵EF=AE=5,∴BD=5,
∴CD=5+3=8;②如图:
当点E在直线BC上方时,以点E为圆心,EC长为半径画弧,交直线BC于点D,
过点E作,延长CA,交EF于点F,∵,
∴∠EFC=∠ACB,∠FEC=∠ECD
∵∠ACB=∠B,
∴∠EFC=∠B=60°,
∵∠FAE=∠BAC=60°,
∴△AEF为等边三角形,∴EF=AE=5,
∵DE=CE,∴∠ECD=∠EDC,∴∠FEC=∠EDC,
在△BDE和△EFC中
∠BDE=∠CEF, ∠DBE=∠AFE,DE=CE
∴△BDE≌△EFC,∴BD=EF=5,
∴CD=BD-BC=5-3=2,综上:CD=8或2.
26.(1)证明:∵△ABC是等边三角形
∴AB=BC∴∠ABC=∠BAC=∠C=∠AFE=60°
∵∠AFE=∠BAF+∠ABF∠ABC=∠CBE+∠ABF
∴∠BAF+∠ABF=∠CBE+∠ABF
∵∠ABF是公共角
∴∠BAD=∠CBE在△ABD和△BCE中
∵∠BAD=∠CBE,AB=BC,∠ABD=∠BCE
∴△ABD≌BCE(ASA)∴AD=BE.
(2)证明:∵△ABC是等边三角形,
∴AC=BC,∠BAC=60°
∵CF为△ABC的高线
∴CF⊥AB
∴∠AFC=90°
∴∠ACF=90°-∠BAC=30°
∴AC=BC=2AF
∵BD=CE
∴CD=BC+BD=2AF+CE.
(3)解:如图,延长BE至H,使AF=FH,连接AH和CH.
∵∠AFE=60°
∴△AFH是等边三角形
∴AF=AH,∠BAC=∠FAH=60°
∴∠BAC-∠CAD=∠FAH-∠CAD
又∵∠CAD为公共边
∴∠BAF=∠CAH
在△BAF和△CAH中
∵AB=AC,∠BAF=∠CAH,AF=AH
∴△BAF≌△CAH(SAS)
∴∠ABF=∠ACH,BF=CH.
由(1)知∠ABC=∠BAC=60°,∠BAD=∠CBE
∴∠BAC-∠BAF=∠ABC-∠CBE,即∠ABF=∠CAD=∠ACH
∴AF∥CH.∠AFC+∠FCH=180°
∵CF为△ABC的高线
∴CF⊥AB
∴∠AFC=90°
∴∠FCH=90°
又∵∠AFE=60°
∴∠CFH=30°
∴AF=FH=2CH=2BF=6
∴AD=AF+DF=7由(1)知AD=BE=7
∴EF=BE-BF=7-3=4.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
