苏科版八年级数学上册试题 第6章 一次函数综合测试卷 (含详解)
文档属性
| 名称 | 苏科版八年级数学上册试题 第6章 一次函数综合测试卷 (含详解) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-06 18:46:50 | ||
图片预览





文档简介
第6章《一次函数》综合测试卷
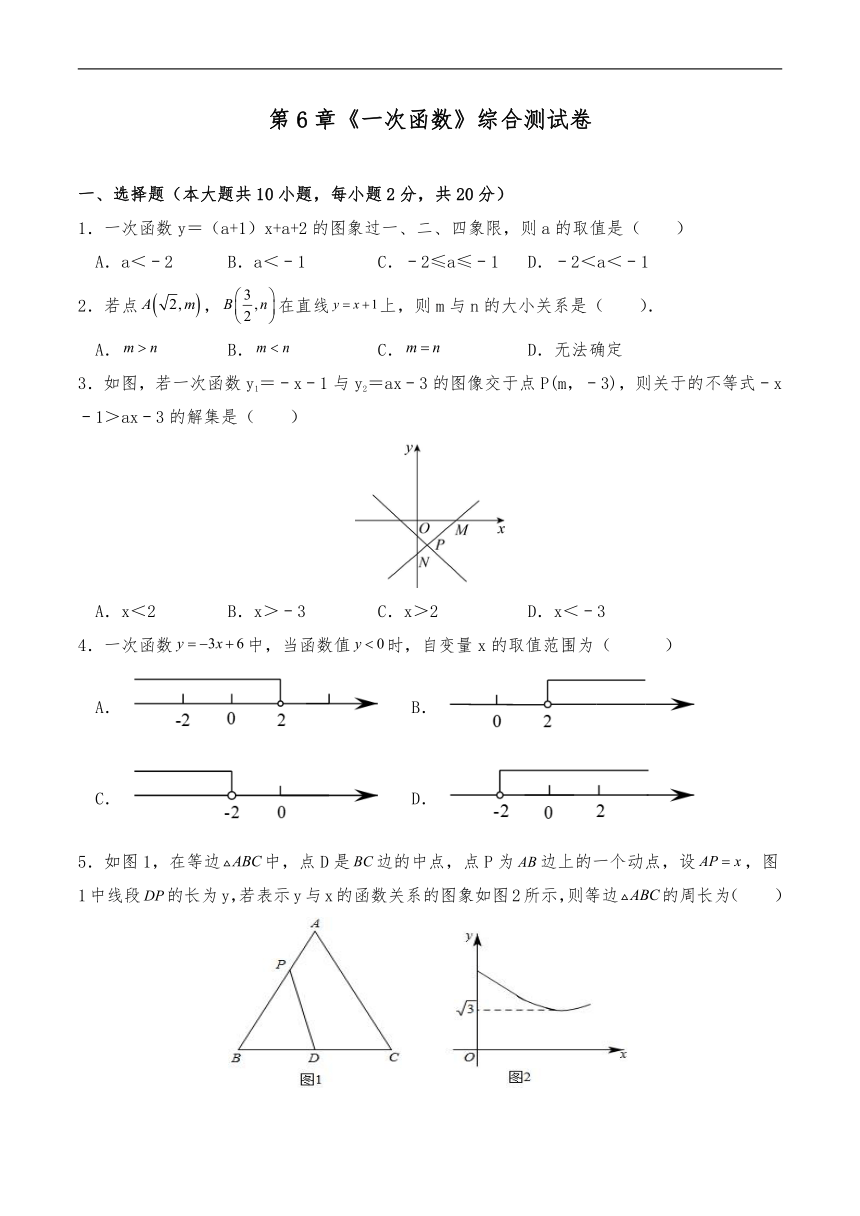
一、选择题(本大题共10小题,每小题2分,共20分)
1.一次函数y=(a+1)x+a+2的图象过一、二、四象限,则a的取值是( )
A.a<﹣2 B.a<﹣1 C.﹣2≤a≤﹣1 D.﹣2<a<﹣1
2.若点,在直线上,则m与n的大小关系是( ).
A. B. C. D.无法确定
3.如图,若一次函数y1=﹣x﹣1与y2=ax﹣3的图像交于点P(m,﹣3),则关于的不等式﹣x﹣1>ax﹣3的解集是( )
A.x<2 B.x>﹣3 C.x>2 D.x<﹣3
4.一次函数中,当函数值时,自变量x的取值范围为( )
A. B.
C. D.
5.如图1,在等边中,点D是边的中点,点P为边上的一个动点,设,图1中线段的长为y,若表示y与x的函数关系的图象如图2所示,则等边的周长为( )
A.4 B. C.12 D.
6.如图,点A,B,C在一次函数y=-2x+b的图象上,它们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积和是( )
A.1 B.3 C.3(b-1) D.
7.如图,直线与直线相交于点P,若不等式的解集是,则的值等于( )
A. B. C.3 D.
8.如图,一次函数与一次函数的图象交于P(1,3),则下列说法正确的个数是( )个
(1)方程的解是
(2)方程组的解是
(3)不等式的解集是
(4)不等式的解集是.
A.1 B.2 C.3 D.4
9.在地球中纬度地区,从地面到高空大约之间,气温随高度的升高而下降,每升高,气温大约下降;高于但不高于,气温几乎不再变化,某城市地处中纬度地区,该市某日的地面气温为,设该城市距离地面高度为处的气温为,则与的函数图像是( )
A. B.
C. D.
10.如图,在平面直角坐标系中,点是直线与直线的交点,点B是直线与y轴的交点,点P是x轴上的一个动点,连接PA,PB,则的最小值是( )
A.6 B. C.9 D.
二、填空题(本大题共6小题,每小题2分,共12分)
11.已知正比例函,当时,.则比例系数k=__________.
12.若是正比例函数,则______.
13.若直线是由直线向下平移了3个单位长度得到的,则kb=______.
14.直线y=kx+b(k≠0)平行于直线且经过点,那么这条直线的解析式是______.
15.如图,直线y=﹣x+7与两坐标轴分别交于A、B两点,点C的坐标是(1,0),DE分别是AB、OA上的动点,当△CDE的周长最小时,点E的坐标是 _____.
16.如图,将正方形置于平面直角坐标系中,其中,,边在轴上,直线与正方形的边有两个交点、,当时,的取值范围是__.
三、解答题(本大题共10题,共68分)
17.(4分)判断三点A(3,1),B(0,-2),C(4,2)是否在同一条直线上.
18.(4分)在平面直角坐标系中,一次函数的图像经过和.
(1)求一次函数解析式.
(2)当,求y的取值范围.
19.(6分)小明从A地出发向B地行走,同时晓阳从B地出发向A地行走,小明、晓阳离A地的距离y(千米)与已用时间x(分钟)之间的函数关系分别如图中、所示.
(1)小明与晓阳出发几分钟时相遇?
(2)求晓阳到达A地的时间.
20.(6分)如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过A(-6,0),B(0,3)两点,点C在直线AB上,C的纵坐标为4.
(1)求k、b的值及点C坐标;
(2)若点D为直线AB上一动点,且△OBC与△OAD的面积相等,试求点D的坐标.
21.(8分)如图,直线与直线相交于点.
(1)求a,b的值;
(2)求△ADC的面积;
(3)根据图象,写出关于x的不等式的解集.
22.(8分)定义:在平面直角坐标系中,对于任意一点如果满足,我们就把点称作“和谐点”.
(1)在直线上的“和谐点”为________;
(2)求一次函数的图象上的“和谐点”坐标;
(3)已知点,点的坐标分别为,,如果线段上始终存在“和谐点”,直接写出的取值范围是________.
23.(6分)某校开展爱心义卖活动,同学们决定将销售获得的利润捐献给福利院.初二某班的同学们准备制作A、B两款挂件来进行销售.已知制作3个A款挂件、5个B款挂件所需成本为46元,制作5个A款挂件、10个B款挂件所需成本为85元.已知A、B两款挂件的售价如下表:
手工制品 A款挂件 B款挂件
售价(元/个) 12 8
(1)求制作一个A款挂件、一个B款挂件所需的成本分别为多少元?
(2)若该班级共有40名学生.计划每位同学制作2个A款挂件或3个B款挂件,制作的总成本不超过590元,且制作B款挂件的数量不少于A款挂件的2倍.设安排m人制作A款挂件,请说明如何安排,使得总利润最大,最大利润是多少?
24.(6分)甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图像解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式;
25.(10分)如图,在平面直角坐标系中,两个全等的直角三角形的直角顶点及一条直角边重合,点在第二象限内,点、点在轴的负半轴上,,.
(1)求点的坐标;
(2)如图,将绕点按顺时针方向旋转到的位置,其中交直线于点,分别交直线、于点、,则除外,还有哪几对全等的三角形,请直接写出答案;(不再另外添加辅助线)(3)在(2)的基础上,将绕点按顺时针方向继续旋转,当的面积为时,求直线的函数表达式.
26.(10分)在平面直角坐标系中,对于点,给出如下定义:当点满足时,称点是点的等和点,已知点.
(1)在中,点的等和点有__________;
(2)点在直线上,若点的等和点也是点的等和点,求点的坐标;
(3)已知点和线段,点C也在 x轴上且满足,线段上总存在线段上每个点的等和点.若的最小值为5,直接写出的值.
答案
一、选择题
1.D
【解析】解:∵一次函数y=(a+1)x+a+2的图象过一、二、四象限,
∴a+1<0,a+2>0
解得-2<a<-1.
故选:D.
2.B
【解析】∵一次函数中,
∴随的增大而增大
又∵
∴
故选:B.
3.A
【解析】解:由题意,将点代入一次函数得:,
解得,
不等式表示的是一次函数的图像位于一次函数的图像上方,
则由函数图像得:,
故选:A.
4.B
【解析】解:∵一次函数y=-3x+6,
∴当y=0时,x=2,y随x的增大而减小,
∴当函数值y<0时,自变量x的取值范围为x>2,
在数轴上表示为: ,
故选:B.
5.C
【解析】解:由图2可得y最小值=,
∵△ABC为等边三角形,分析图1可知,当P点运动到DP⊥AB时,DP长为最小值,
∴此时DP=,
∵DP⊥AB,
∴,
∵△ABC为等边三角形,
∵∠B=60°,AB=BC=AC,
∴,
∴BD=2BP,
根据勾股定理可知,,
∴,
∴或(舍去),,
∵D为BC的中点,
∴BC=4,
∴AB=BC=AC=4,
∴等边△ABC的周长为12.
故选:C.
6.B
【解析】解:由题意可得A、C的坐标分别为(-1,b+2)、(2,b-4),
又阴影部分为三个有一直角边都是1,另一直角边的长度和为A点纵坐标与C点纵坐标之差的三角形,所以阴影部分的面积为:,
故选B.
7.B
【解析】∵kx+b (x+3)<0的解集是x> 1
∴P点横坐标是 1,则纵坐标为2
则P( 1,2),
由图可知直线m2与y轴的交点坐标是(0,-1),
把P( 1,2)和(0, 1)代入
∴
∴
故选:B.
8.C
【解析】解:因为一次函数与一次函数的图象交于P(1,3),
所以(1)方程ax+b=3的一个解是x=1,正确;
(2)方程组的解是,错误;
(3)不等式ax+b>kx十4的解集是x>1,正确;
(4)不等式4>kx十4>ax+b的解集是0故选:C.
9.B
【解析】解:由题意可知,当高度x=0时,y=20℃;
当x=11时,y=20-11×6=-46℃,
∴y=-6x+20()当时,y=-46
根据一次函数的性质可知,只有B选项的图像符合题意.
故答案为:B.
10.D
【解析】解:作点A关于x轴的对称点,连接,如图所示:
则PA+PB的最小值即为的长,
将点A(3,a)代入y=2x,
得a=2×3=6,
∴点A坐标为(3,6),
将点A(3,6)代入y=x+b,
得3+b=6,
解得b=3,
∴点B坐标为(0,3),
根据轴对称的性质,可得点A'坐标为(3,-6)∴,
∴PA+PB的最小值为.
故选:D.
二、填空题
11.-5
【解析】解:把,代入得:,
∴.
故答案为:.
12.
【解析】∵是正比例函数,
∴,,,
∴,,
∴,
故答案为:.
13.8
【解析】解∶ 直线向下平移了3个单位长度得到,
∴k=-2,b=-4,
∴.
故答案为:8.
14.
【解析】解:根据题意得,
将代入得b=2,
直线解析式为,
故答案为:.
15.10
【解析】解:如图,点C关于OA的对称点(-1,0),点C关于直线AB的对称点,
∵直线AB的解析式为y=-x+7,
∴直线C的解析式为y=x-1,
由,得
∴F(4,3),
∵F是C中点,
∴可得(7,6).
连接与AO交于点E,与AB交于点D,此时△DEC周长最小,
△DEC的周长=DE+EC+CD=E+ED+D===10.
故答案为10.
16.或且
【解析】解:如图,设BC与y轴交于点M,
,,,
∴E点不在AD边上,
;
①如果,那么点E在AB边或线段BM上,
当点E在AB边且时,
由勾股定理得,,
,
,,
当直线经过点,时,.
,
,
当点E在线段BM上时,,
,符合题意;
②如果,那么点E在CD边或线段CM上,
当点E在CD边且时,E与D重合;
当时,由勾股定理得,,
,
,此时E与C重合,
当直线经过点时,.
当点E在线段CM上时,,
且,符合题意;
综上,当时,的取值范围是或且,
故答案为:或且.
三、解答题
17.解:设过A,B两点的直线的表达式为y=kx+b.由题意可知,
解得
∴过A,B两点的直线的表达式为y=x-2.
∵当x=4时,y=4—2=2.
∴点C(4,2)在直线y=x-2上.
∴三点A(3,1), B(0,-2),C(4,2)在同一条直线上.
18.(1)解:设一次函数解析式为
∵一次函数的图像经过和
解得:
∴一次函数解析式为;
(2)解:由(1)得:,
一次函数的图像y随x的增大而减小,
当时,,
当时,,
当时,.
19.(1)解:设的解析式为:.
∵函数的图象过,
,
即,
,
当时,,
∴小明与晓阳出发12分钟时相遇.
(2)解:∵晓阳的速度为(千米/分钟),
∴晓阳到达A地的时间为分钟.
20.(1)解:(1)依题意得:
解得
∴
∵点C在直线AB上,C的纵坐标为4
点C坐标为(2,4)(2)∵B(0,3),C的纵坐标为4
∴
∴
设点D点坐标为,又点A(-6,0)∴
解得
当时
当时
∴点D坐标为(-4,1)或(-8,-1)
21.(1)解∶∵直线经过点,
∴,
∴点B的坐标为,
∵直线经过点,
∴,
∴;
(2)解:∵,
∴直线AD的解析式为,
令,则,
令,则,
∴A(0,4),D(4,0),
∴OA=OD=4,
直线与x轴交于点C,
令,则,
∴C(-2,0),
∴OC=2,
∴CD=6,
∴;
(3)解:点B的坐标为,点D的坐标为,
∴根据图象可得:关于x的不等式的解集为.
22.(1)解:由题意得:,
解得:x=3或x=-3,
在直线上的“和谐点”为:(3,6)和(-3,6);
(2)由“和谐点”的定义可知或,
联立,解得:,
联立,解得:,
所以一次函数的图象上的“和谐点”坐标为(,)和(-2,4);
(3)如图为的函数图象的简图,PQy轴,
①当m>0时,
令,解得:,
令,解得:,
由图可知,如果线段上始终存在“和谐点”,的取值范围是;
②当m<0时,
令,解得:,
令,解得:,
由图可知,如果线段上始终存在“和谐点”,的取值范围是,
综上,当或时,线段上始终存在“和谐点”.
23.(1)由题意可设制作一个A款挂件、一个B款挂件所需的成本分别为x、y元,
则,
解得将①得6x+10y=92,
再将①②得x=7,再将x=7回代②得y=5,
解得,
答:制作一个A款挂件、一个B款挂件所需的成本分别7元、5元;
(2)由题意得设(40)人制作B款挂件,总利润为w元,
则w=(12),
∴w随m的增大而增大,
∵制作的总成本不超过590元,且制作B款挂件的数量不少于A款挂件的2倍,
∴,
解得10
∵m为正整数,
∴当m=17时,w取得最大值,
此时w=377,(40)=23,
答:当安排17人制作A款挂件,23人制作B款挂件时,总利润最大,最大利润为377元.
24.(1)根据图像信息:货车的速度(千米/时).
∵轿车到达乙地的时间为货车出发后4.5小时,
∴轿车到达乙地时,货车行驶的路程为:(千米).
此时,货车距乙地的路程为:(千米).
答:轿车到达乙地后,货车距乙地30千米;
(2)设CD段函数解析式为()().
∵,在其图像上,
∴,解得.
∴CD段函数解析式:;
25.(1)解:在中,,,
所以,
则;
(2)解:或或
(3)解:如图1,过点作于点.
∵,
∴.
∵在Rt△AOC中,,IOC=2,∠ACO=90°,
∴,
∴点A(-2,),
设直线OA的解析是为,则,
∴,
∴直线OA的解析式为,
令y=,则,解得x=,
∴点的坐标为.
设直线的函数表达式为, ,解得 .
∴.
同理,如图2所示,点的坐标为.
设直线的函数表达式为,则
,解得 .
∴.
综上所得或.
26.(1)Q1(0,3),则0+3=3+0,
∴Q1(0,3)是点P的等和点;
Q2(1,4),则1+3=4+0,
∴Q2(1,4)是点P的等和点;
Q3(-2,-1),则-2+3≠-1+0,
∴Q3(-2,-1)不是点P的等和点;
故答案为:Q1,Q2;
(2)设点P(3,0)的等和点为(m,n),
∴3+m=n,有m-n=-3,
∵A在直线y=-x+5上,
∴设A(t,-t+5),
则A点的等和点为(m,n),
∴t+m=-t+5+n,由m-n=-2t+5,
∴-3=-2t+5,
解得t=4,
∴A(4,1);
(3)∵P(3,0),
∴P点的等和点在直线l:y=x+3上,
∵B(b,0),BC=1,且C在x轴上,
∴C(b-1,0)或(b+1,0)∴C点的等和点在直线l1:y=x+b-1或y=x+b+1上,
设直线l1与y轴交于C',直线l与y轴交于P',则C'(0,b-1)或(0,b+1),P'(0,3),
①当点C在点B的左边时,如图1,直线CC'与直线l交于N,当M与C'重合时,MN最小为5,
∵△MNP'是等腰直角三角形,
∴P'C'=5,
∴b-1=5+3,
∴b=4+5;
如图2,同理得P'M=5,
∴3+(1-b)=5,
∴b=4-5;
②当点C在点B的右边时,如图3,
同理得:P'M=5,
∴5-3=-b-1,
∴b=2-5;
如图4,同理得:P'M=5,
∴5+3=b+1,
∴b=2+5;
综上,b的值是2 5或4 5或4+5或2+5.
一、选择题(本大题共10小题,每小题2分,共20分)
1.一次函数y=(a+1)x+a+2的图象过一、二、四象限,则a的取值是( )
A.a<﹣2 B.a<﹣1 C.﹣2≤a≤﹣1 D.﹣2<a<﹣1
2.若点,在直线上,则m与n的大小关系是( ).
A. B. C. D.无法确定
3.如图,若一次函数y1=﹣x﹣1与y2=ax﹣3的图像交于点P(m,﹣3),则关于的不等式﹣x﹣1>ax﹣3的解集是( )
A.x<2 B.x>﹣3 C.x>2 D.x<﹣3
4.一次函数中,当函数值时,自变量x的取值范围为( )
A. B.
C. D.
5.如图1,在等边中,点D是边的中点,点P为边上的一个动点,设,图1中线段的长为y,若表示y与x的函数关系的图象如图2所示,则等边的周长为( )
A.4 B. C.12 D.
6.如图,点A,B,C在一次函数y=-2x+b的图象上,它们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积和是( )
A.1 B.3 C.3(b-1) D.
7.如图,直线与直线相交于点P,若不等式的解集是,则的值等于( )
A. B. C.3 D.
8.如图,一次函数与一次函数的图象交于P(1,3),则下列说法正确的个数是( )个
(1)方程的解是
(2)方程组的解是
(3)不等式的解集是
(4)不等式的解集是.
A.1 B.2 C.3 D.4
9.在地球中纬度地区,从地面到高空大约之间,气温随高度的升高而下降,每升高,气温大约下降;高于但不高于,气温几乎不再变化,某城市地处中纬度地区,该市某日的地面气温为,设该城市距离地面高度为处的气温为,则与的函数图像是( )
A. B.
C. D.
10.如图,在平面直角坐标系中,点是直线与直线的交点,点B是直线与y轴的交点,点P是x轴上的一个动点,连接PA,PB,则的最小值是( )
A.6 B. C.9 D.
二、填空题(本大题共6小题,每小题2分,共12分)
11.已知正比例函,当时,.则比例系数k=__________.
12.若是正比例函数,则______.
13.若直线是由直线向下平移了3个单位长度得到的,则kb=______.
14.直线y=kx+b(k≠0)平行于直线且经过点,那么这条直线的解析式是______.
15.如图,直线y=﹣x+7与两坐标轴分别交于A、B两点,点C的坐标是(1,0),DE分别是AB、OA上的动点,当△CDE的周长最小时,点E的坐标是 _____.
16.如图,将正方形置于平面直角坐标系中,其中,,边在轴上,直线与正方形的边有两个交点、,当时,的取值范围是__.
三、解答题(本大题共10题,共68分)
17.(4分)判断三点A(3,1),B(0,-2),C(4,2)是否在同一条直线上.
18.(4分)在平面直角坐标系中,一次函数的图像经过和.
(1)求一次函数解析式.
(2)当,求y的取值范围.
19.(6分)小明从A地出发向B地行走,同时晓阳从B地出发向A地行走,小明、晓阳离A地的距离y(千米)与已用时间x(分钟)之间的函数关系分别如图中、所示.
(1)小明与晓阳出发几分钟时相遇?
(2)求晓阳到达A地的时间.
20.(6分)如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过A(-6,0),B(0,3)两点,点C在直线AB上,C的纵坐标为4.
(1)求k、b的值及点C坐标;
(2)若点D为直线AB上一动点,且△OBC与△OAD的面积相等,试求点D的坐标.
21.(8分)如图,直线与直线相交于点.
(1)求a,b的值;
(2)求△ADC的面积;
(3)根据图象,写出关于x的不等式的解集.
22.(8分)定义:在平面直角坐标系中,对于任意一点如果满足,我们就把点称作“和谐点”.
(1)在直线上的“和谐点”为________;
(2)求一次函数的图象上的“和谐点”坐标;
(3)已知点,点的坐标分别为,,如果线段上始终存在“和谐点”,直接写出的取值范围是________.
23.(6分)某校开展爱心义卖活动,同学们决定将销售获得的利润捐献给福利院.初二某班的同学们准备制作A、B两款挂件来进行销售.已知制作3个A款挂件、5个B款挂件所需成本为46元,制作5个A款挂件、10个B款挂件所需成本为85元.已知A、B两款挂件的售价如下表:
手工制品 A款挂件 B款挂件
售价(元/个) 12 8
(1)求制作一个A款挂件、一个B款挂件所需的成本分别为多少元?
(2)若该班级共有40名学生.计划每位同学制作2个A款挂件或3个B款挂件,制作的总成本不超过590元,且制作B款挂件的数量不少于A款挂件的2倍.设安排m人制作A款挂件,请说明如何安排,使得总利润最大,最大利润是多少?
24.(6分)甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图像解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式;
25.(10分)如图,在平面直角坐标系中,两个全等的直角三角形的直角顶点及一条直角边重合,点在第二象限内,点、点在轴的负半轴上,,.
(1)求点的坐标;
(2)如图,将绕点按顺时针方向旋转到的位置,其中交直线于点,分别交直线、于点、,则除外,还有哪几对全等的三角形,请直接写出答案;(不再另外添加辅助线)(3)在(2)的基础上,将绕点按顺时针方向继续旋转,当的面积为时,求直线的函数表达式.
26.(10分)在平面直角坐标系中,对于点,给出如下定义:当点满足时,称点是点的等和点,已知点.
(1)在中,点的等和点有__________;
(2)点在直线上,若点的等和点也是点的等和点,求点的坐标;
(3)已知点和线段,点C也在 x轴上且满足,线段上总存在线段上每个点的等和点.若的最小值为5,直接写出的值.
答案
一、选择题
1.D
【解析】解:∵一次函数y=(a+1)x+a+2的图象过一、二、四象限,
∴a+1<0,a+2>0
解得-2<a<-1.
故选:D.
2.B
【解析】∵一次函数中,
∴随的增大而增大
又∵
∴
故选:B.
3.A
【解析】解:由题意,将点代入一次函数得:,
解得,
不等式表示的是一次函数的图像位于一次函数的图像上方,
则由函数图像得:,
故选:A.
4.B
【解析】解:∵一次函数y=-3x+6,
∴当y=0时,x=2,y随x的增大而减小,
∴当函数值y<0时,自变量x的取值范围为x>2,
在数轴上表示为: ,
故选:B.
5.C
【解析】解:由图2可得y最小值=,
∵△ABC为等边三角形,分析图1可知,当P点运动到DP⊥AB时,DP长为最小值,
∴此时DP=,
∵DP⊥AB,
∴,
∵△ABC为等边三角形,
∵∠B=60°,AB=BC=AC,
∴,
∴BD=2BP,
根据勾股定理可知,,
∴,
∴或(舍去),,
∵D为BC的中点,
∴BC=4,
∴AB=BC=AC=4,
∴等边△ABC的周长为12.
故选:C.
6.B
【解析】解:由题意可得A、C的坐标分别为(-1,b+2)、(2,b-4),
又阴影部分为三个有一直角边都是1,另一直角边的长度和为A点纵坐标与C点纵坐标之差的三角形,所以阴影部分的面积为:,
故选B.
7.B
【解析】∵kx+b (x+3)<0的解集是x> 1
∴P点横坐标是 1,则纵坐标为2
则P( 1,2),
由图可知直线m2与y轴的交点坐标是(0,-1),
把P( 1,2)和(0, 1)代入
∴
∴
故选:B.
8.C
【解析】解:因为一次函数与一次函数的图象交于P(1,3),
所以(1)方程ax+b=3的一个解是x=1,正确;
(2)方程组的解是,错误;
(3)不等式ax+b>kx十4的解集是x>1,正确;
(4)不等式4>kx十4>ax+b的解集是0
9.B
【解析】解:由题意可知,当高度x=0时,y=20℃;
当x=11时,y=20-11×6=-46℃,
∴y=-6x+20()当时,y=-46
根据一次函数的性质可知,只有B选项的图像符合题意.
故答案为:B.
10.D
【解析】解:作点A关于x轴的对称点,连接,如图所示:
则PA+PB的最小值即为的长,
将点A(3,a)代入y=2x,
得a=2×3=6,
∴点A坐标为(3,6),
将点A(3,6)代入y=x+b,
得3+b=6,
解得b=3,
∴点B坐标为(0,3),
根据轴对称的性质,可得点A'坐标为(3,-6)∴,
∴PA+PB的最小值为.
故选:D.
二、填空题
11.-5
【解析】解:把,代入得:,
∴.
故答案为:.
12.
【解析】∵是正比例函数,
∴,,,
∴,,
∴,
故答案为:.
13.8
【解析】解∶ 直线向下平移了3个单位长度得到,
∴k=-2,b=-4,
∴.
故答案为:8.
14.
【解析】解:根据题意得,
将代入得b=2,
直线解析式为,
故答案为:.
15.10
【解析】解:如图,点C关于OA的对称点(-1,0),点C关于直线AB的对称点,
∵直线AB的解析式为y=-x+7,
∴直线C的解析式为y=x-1,
由,得
∴F(4,3),
∵F是C中点,
∴可得(7,6).
连接与AO交于点E,与AB交于点D,此时△DEC周长最小,
△DEC的周长=DE+EC+CD=E+ED+D===10.
故答案为10.
16.或且
【解析】解:如图,设BC与y轴交于点M,
,,,
∴E点不在AD边上,
;
①如果,那么点E在AB边或线段BM上,
当点E在AB边且时,
由勾股定理得,,
,
,,
当直线经过点,时,.
,
,
当点E在线段BM上时,,
,符合题意;
②如果,那么点E在CD边或线段CM上,
当点E在CD边且时,E与D重合;
当时,由勾股定理得,,
,
,此时E与C重合,
当直线经过点时,.
当点E在线段CM上时,,
且,符合题意;
综上,当时,的取值范围是或且,
故答案为:或且.
三、解答题
17.解:设过A,B两点的直线的表达式为y=kx+b.由题意可知,
解得
∴过A,B两点的直线的表达式为y=x-2.
∵当x=4时,y=4—2=2.
∴点C(4,2)在直线y=x-2上.
∴三点A(3,1), B(0,-2),C(4,2)在同一条直线上.
18.(1)解:设一次函数解析式为
∵一次函数的图像经过和
解得:
∴一次函数解析式为;
(2)解:由(1)得:,
一次函数的图像y随x的增大而减小,
当时,,
当时,,
当时,.
19.(1)解:设的解析式为:.
∵函数的图象过,
,
即,
,
当时,,
∴小明与晓阳出发12分钟时相遇.
(2)解:∵晓阳的速度为(千米/分钟),
∴晓阳到达A地的时间为分钟.
20.(1)解:(1)依题意得:
解得
∴
∵点C在直线AB上,C的纵坐标为4
点C坐标为(2,4)(2)∵B(0,3),C的纵坐标为4
∴
∴
设点D点坐标为,又点A(-6,0)∴
解得
当时
当时
∴点D坐标为(-4,1)或(-8,-1)
21.(1)解∶∵直线经过点,
∴,
∴点B的坐标为,
∵直线经过点,
∴,
∴;
(2)解:∵,
∴直线AD的解析式为,
令,则,
令,则,
∴A(0,4),D(4,0),
∴OA=OD=4,
直线与x轴交于点C,
令,则,
∴C(-2,0),
∴OC=2,
∴CD=6,
∴;
(3)解:点B的坐标为,点D的坐标为,
∴根据图象可得:关于x的不等式的解集为.
22.(1)解:由题意得:,
解得:x=3或x=-3,
在直线上的“和谐点”为:(3,6)和(-3,6);
(2)由“和谐点”的定义可知或,
联立,解得:,
联立,解得:,
所以一次函数的图象上的“和谐点”坐标为(,)和(-2,4);
(3)如图为的函数图象的简图,PQy轴,
①当m>0时,
令,解得:,
令,解得:,
由图可知,如果线段上始终存在“和谐点”,的取值范围是;
②当m<0时,
令,解得:,
令,解得:,
由图可知,如果线段上始终存在“和谐点”,的取值范围是,
综上,当或时,线段上始终存在“和谐点”.
23.(1)由题意可设制作一个A款挂件、一个B款挂件所需的成本分别为x、y元,
则,
解得将①得6x+10y=92,
再将①②得x=7,再将x=7回代②得y=5,
解得,
答:制作一个A款挂件、一个B款挂件所需的成本分别7元、5元;
(2)由题意得设(40)人制作B款挂件,总利润为w元,
则w=(12),
∴w随m的增大而增大,
∵制作的总成本不超过590元,且制作B款挂件的数量不少于A款挂件的2倍,
∴,
解得10
∵m为正整数,
∴当m=17时,w取得最大值,
此时w=377,(40)=23,
答:当安排17人制作A款挂件,23人制作B款挂件时,总利润最大,最大利润为377元.
24.(1)根据图像信息:货车的速度(千米/时).
∵轿车到达乙地的时间为货车出发后4.5小时,
∴轿车到达乙地时,货车行驶的路程为:(千米).
此时,货车距乙地的路程为:(千米).
答:轿车到达乙地后,货车距乙地30千米;
(2)设CD段函数解析式为()().
∵,在其图像上,
∴,解得.
∴CD段函数解析式:;
25.(1)解:在中,,,
所以,
则;
(2)解:或或
(3)解:如图1,过点作于点.
∵,
∴.
∵在Rt△AOC中,,IOC=2,∠ACO=90°,
∴,
∴点A(-2,),
设直线OA的解析是为,则,
∴,
∴直线OA的解析式为,
令y=,则,解得x=,
∴点的坐标为.
设直线的函数表达式为, ,解得 .
∴.
同理,如图2所示,点的坐标为.
设直线的函数表达式为,则
,解得 .
∴.
综上所得或.
26.(1)Q1(0,3),则0+3=3+0,
∴Q1(0,3)是点P的等和点;
Q2(1,4),则1+3=4+0,
∴Q2(1,4)是点P的等和点;
Q3(-2,-1),则-2+3≠-1+0,
∴Q3(-2,-1)不是点P的等和点;
故答案为:Q1,Q2;
(2)设点P(3,0)的等和点为(m,n),
∴3+m=n,有m-n=-3,
∵A在直线y=-x+5上,
∴设A(t,-t+5),
则A点的等和点为(m,n),
∴t+m=-t+5+n,由m-n=-2t+5,
∴-3=-2t+5,
解得t=4,
∴A(4,1);
(3)∵P(3,0),
∴P点的等和点在直线l:y=x+3上,
∵B(b,0),BC=1,且C在x轴上,
∴C(b-1,0)或(b+1,0)∴C点的等和点在直线l1:y=x+b-1或y=x+b+1上,
设直线l1与y轴交于C',直线l与y轴交于P',则C'(0,b-1)或(0,b+1),P'(0,3),
①当点C在点B的左边时,如图1,直线CC'与直线l交于N,当M与C'重合时,MN最小为5,
∵△MNP'是等腰直角三角形,
∴P'C'=5,
∴b-1=5+3,
∴b=4+5;
如图2,同理得P'M=5,
∴3+(1-b)=5,
∴b=4-5;
②当点C在点B的右边时,如图3,
同理得:P'M=5,
∴5-3=-b-1,
∴b=2-5;
如图4,同理得:P'M=5,
∴5+3=b+1,
∴b=2+5;
综上,b的值是2 5或4 5或4+5或2+5.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
