河北省平泉县第四中学人教版九年级数学上册课件:22.1.1二次函数的图像与性质
文档属性
| 名称 | 河北省平泉县第四中学人教版九年级数学上册课件:22.1.1二次函数的图像与性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 565.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-06 00:00:00 | ||
图片预览





文档简介
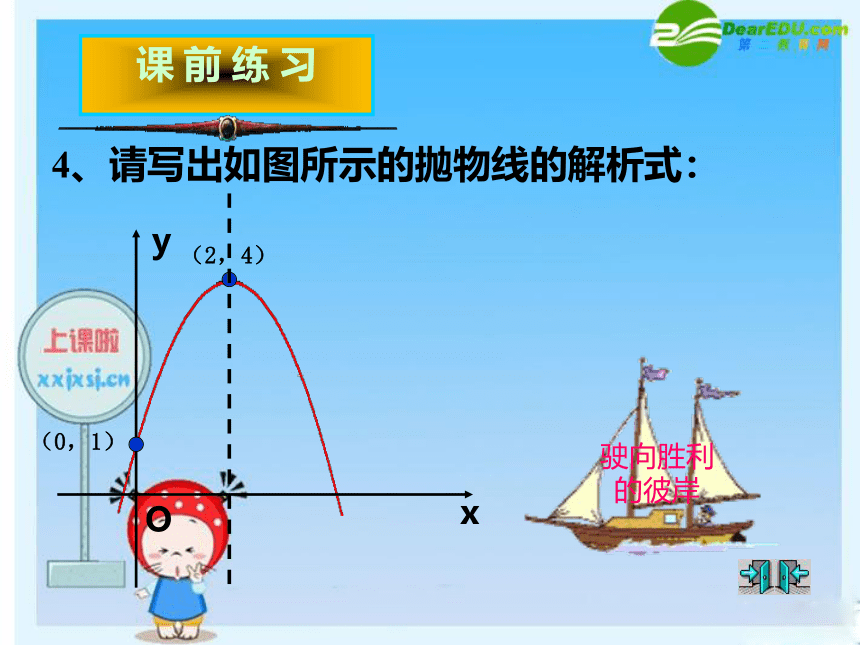
课件22张PPT。二次函数27.2 二次函数的性质二次函数 y=ax2+bx+c 的图像与a,b,c得符号问题平泉四中 毛艳玲1、抛物线y=x2-8x+m的顶点在 x轴上则c= .2、抛物线 y=x2+bx+1的顶点在 y轴上则b= ________ 3、抛物线 y=x2+bx+1对称轴是直线x=2则b= ________ 试一试:驶向胜利的彼岸4、请写出如图所示的抛物线的解析式: 课 前 练 习(0,1)(2,4)xyO 对于二次函数y=ax2+bx+c ( a≠0 )的图象及图象的形状、开口方向、位置又是怎样的?通过变形能否将y=ax2+bx+c转化为
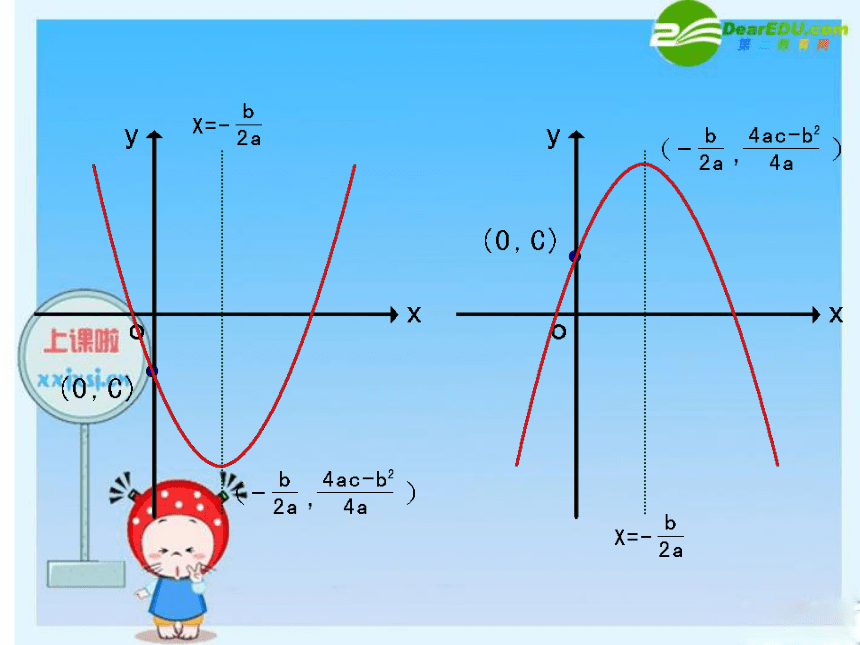
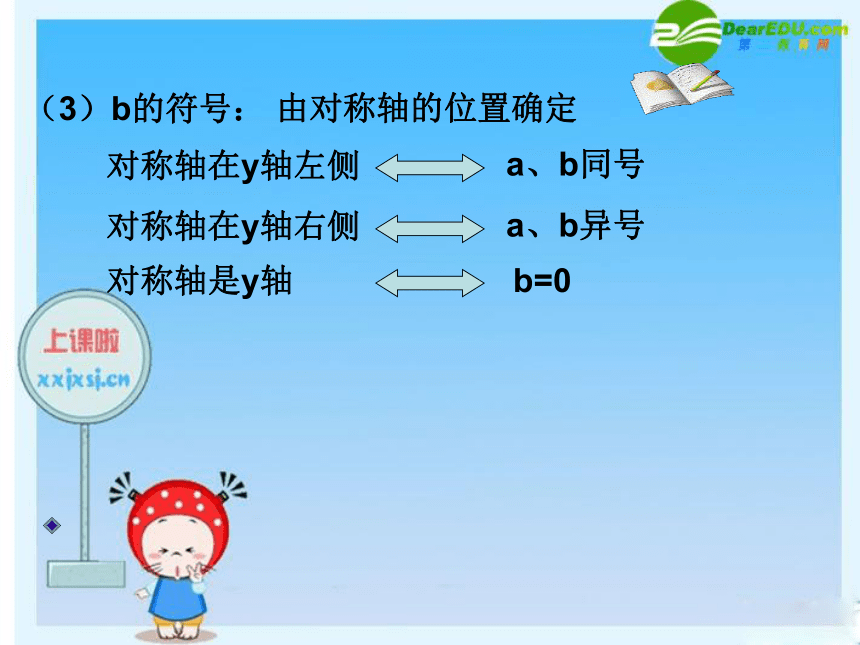
y = a(x+m)2 +k的形式 ?知识点一:抛物线y=ax2+bx+c的符号问题:与y轴的正半轴相交c>0与y轴的负半轴相交 c<0经过坐标原点c=0(1)a的符号:由抛物线的开口方向确定1、抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:xyo a>0,
b<0,
c>0,
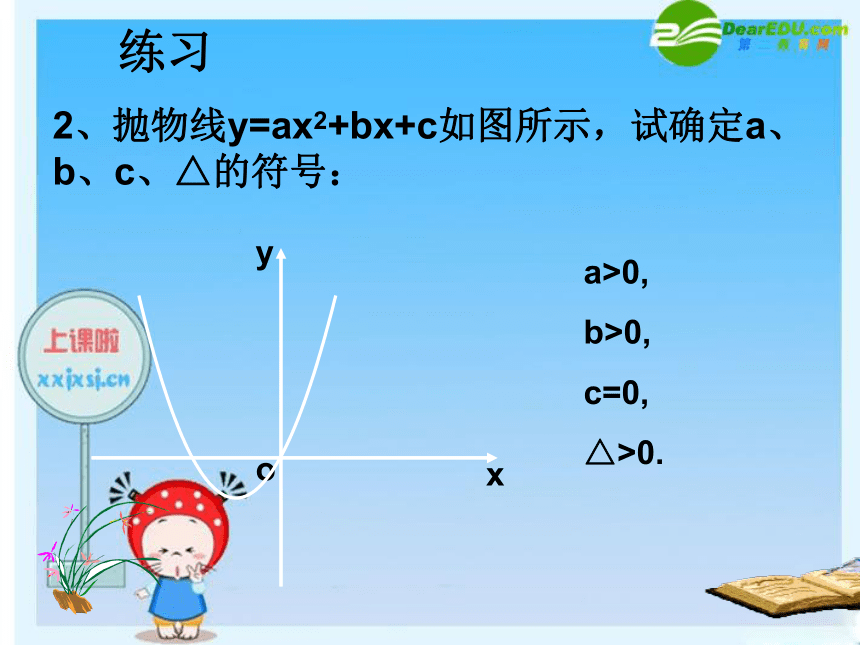
△>0.练习2、抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:xyo a>0,
b>0,
c=0,
△>0.练习3、抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:xyo a<0,
b<0,
c>0,
△>0.练习4、抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:xyo a>0,
b=0,
c>0,
△=0.练习5、抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:xyo a>0,
b=0,
c=0,
△=0.练习6、抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:xyo a<0,
b>0,
c<0,
△<0.练习小结:7、已知:二次函数y=ax2+bx+c的图象如图所示,则点M( ,a)在 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限 xoy a<0,
b>0,
c>0,D练习8、已知:一次函数y=ax+c与二次函数y=ax2+bx+c,它们在同一坐标系中的大致图象是图中的( )(A)(B)(C)(D)C练习9、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①abc>0;②b=2a;
③a+b+c<0;④a+b-c>0; ⑤a-b+c>0正确的个数是 ( )
A、2个 B、3个
C、4个 D、5个C练习知识点二:抛物线y=ax2+bx+c的符号问题:(5)a+b+c的符号:由x=1时抛物线上的点的位置确定点在x轴上方点在x轴下方点在x轴上a+b+c>0a+b+c<0a+b+c=0(6)a-b+c的符号:由x=-1时抛物线上的点的位置确定点在x轴上方点在x轴下方点在x轴上a-b+c>0a-b+c<0a-b+c=010、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①b>0;②c<0;③4a+2b+c > 0;④(a+c)2<b2,其中正确的个数是 ( )
A、4个 B、3个
C、2个 D、1个B练习11、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中下不正确的是 ( )
A、abc>0
B、b2-4ac>0
C、2a+b>0
D、4a-2b+c<0D练习试一试:已知;二次函数y=2x2-(m+1)x+(m-1).
(1)求证:不论m为何值时,函数的图像与x轴总有交点,并指出m为何值时,只有一个交点;
(2)当m为何值时,函数图像过原点,并指出此时函数图像与x轴的另一个交点;
(3)若函数图像的顶点在第四象限,求m的取值范围.
(2)另一个交点坐标为(1,0) (3)当m>-1且m≠3时,抛物线的顶点在第四象限 抛物线y=ax2+bx+c的符号问题:(1)a的符号:由抛物线的开口方向确定小结
y = a(x+m)2 +k的形式 ?知识点一:抛物线y=ax2+bx+c的符号问题:与y轴的正半轴相交c>0与y轴的负半轴相交 c<0经过坐标原点c=0(1)a的符号:由抛物线的开口方向确定1、抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:xyo a>0,
b<0,
c>0,
△>0.练习2、抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:xyo a>0,
b>0,
c=0,
△>0.练习3、抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:xyo a<0,
b<0,
c>0,
△>0.练习4、抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:xyo a>0,
b=0,
c>0,
△=0.练习5、抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:xyo a>0,
b=0,
c=0,
△=0.练习6、抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:xyo a<0,
b>0,
c<0,
△<0.练习小结:7、已知:二次函数y=ax2+bx+c的图象如图所示,则点M( ,a)在 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限 xoy a<0,
b>0,
c>0,D练习8、已知:一次函数y=ax+c与二次函数y=ax2+bx+c,它们在同一坐标系中的大致图象是图中的( )(A)(B)(C)(D)C练习9、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①abc>0;②b=2a;
③a+b+c<0;④a+b-c>0; ⑤a-b+c>0正确的个数是 ( )
A、2个 B、3个
C、4个 D、5个C练习知识点二:抛物线y=ax2+bx+c的符号问题:(5)a+b+c的符号:由x=1时抛物线上的点的位置确定点在x轴上方点在x轴下方点在x轴上a+b+c>0a+b+c<0a+b+c=0(6)a-b+c的符号:由x=-1时抛物线上的点的位置确定点在x轴上方点在x轴下方点在x轴上a-b+c>0a-b+c<0a-b+c=010、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①b>0;②c<0;③4a+2b+c > 0;④(a+c)2<b2,其中正确的个数是 ( )
A、4个 B、3个
C、2个 D、1个B练习11、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中下不正确的是 ( )
A、abc>0
B、b2-4ac>0
C、2a+b>0
D、4a-2b+c<0D练习试一试:已知;二次函数y=2x2-(m+1)x+(m-1).
(1)求证:不论m为何值时,函数的图像与x轴总有交点,并指出m为何值时,只有一个交点;
(2)当m为何值时,函数图像过原点,并指出此时函数图像与x轴的另一个交点;
(3)若函数图像的顶点在第四象限,求m的取值范围.
(2)另一个交点坐标为(1,0) (3)当m>-1且m≠3时,抛物线的顶点在第四象限 抛物线y=ax2+bx+c的符号问题:(1)a的符号:由抛物线的开口方向确定小结
同课章节目录
