河北省平泉县第四中学人教版九年级数学上册课件:22.2二次函数与一元二次方程的关系
文档属性
| 名称 | 河北省平泉县第四中学人教版九年级数学上册课件:22.2二次函数与一元二次方程的关系 |

|
|
| 格式 | zip | ||
| 文件大小 | 46.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-06 00:00:00 | ||
图片预览





文档简介
课件13张PPT。二次函数
与
一元二次方程的关系平泉四中 毛艳玲一、探究探究1、求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标。解:∵A、B在轴上,
∴它们的纵坐标为0,
∴令y=0,则x2-3x+2=0
解得:x1=1,x2=2;
∴A(1,0) , B(2,0)你发现方程 的解x1、x2与A、B的坐标有什么联系?
x2-3x+2=0结论1:方程x2-3x+2=0的解就是抛物线y=x2-3x+2与x轴的两个交点的横坐标。因此,抛物线与一元二次方程是有密切联系的。即:若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与轴的两个交点坐标分别是A( ), B( )x1,0x2,0x探究2、抛物线与X 轴的交点个数能不能用一元二次方程的知识来说明呢?b2-4ac>0b2-4ac=0
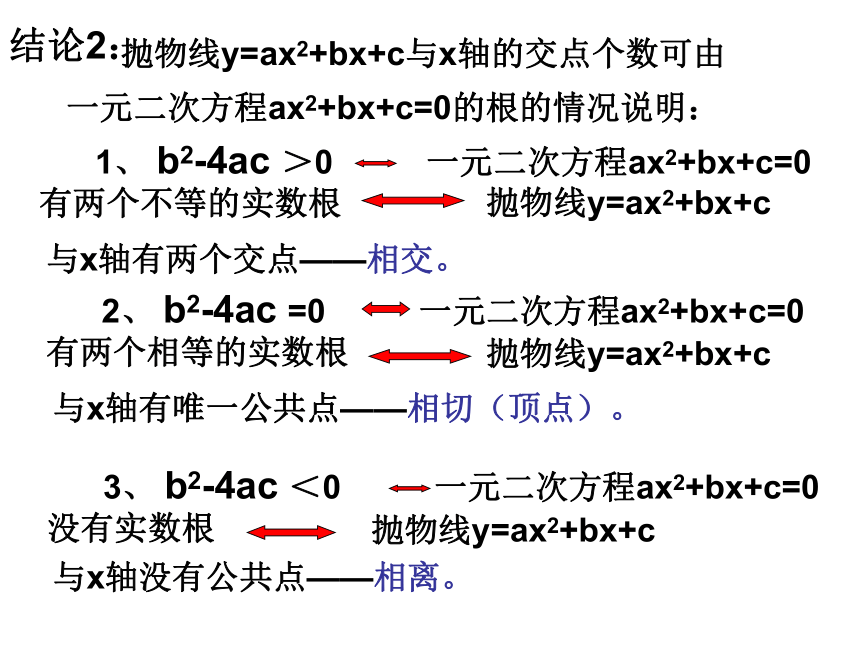
b2-4ac<0OXY结论2:抛物线y=ax2+bx+c抛物线y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况说明: 1、 b2-4ac >0 一元二次方程ax2+bx+c=0
有两个不等的实数根与x轴有两个交点——相交。抛物线y=ax2+bx+c 2、 b2-4ac =0 一元二次方程ax2+bx+c=0
有两个相等的实数根与x轴有唯一公共点——相切(顶点)。抛物线y=ax2+bx+c 3、 b2-4ac <0 一元二次方程ax2+bx+c=0
没有实数根与x轴没有公共点——相离。二、基础训练1、已知抛物线y=x2-6x+a的顶点在x轴上,则a= ;若抛物线与x轴有两个交点,则a的范围是 ;
3、已知抛物线y=x2+px+q与x轴的两个交点为(-2,0),(3,0),则p= ,q= 。2、已知抛物线y=x2-3x+a+1与x轴最多只有一个交点,则a的范围是 。4、判断下列各抛物线是否与x轴相交,如果相交,求出交点的坐标。
(1)y=6x2-2x+1 (2)y=-15x2+14x+8
(3)y=x2-4x+46、抛物线y=ax2+bx+c(a≠0)的图象全部在轴下方的条件是( )
(A)a<0 b2-4ac≤0
(B)a<0 b2-4ac>0
(C)a>0 b2-4ac>0
(D)a<0 b2-4ac<0
D三、例题推荐1、已知二次函数y=x2-kx-2+k.
(1)求证:不论k取何值时,这个二次函数
y=x2-kx-2+k与x轴有两个不同的交点。
(2)如果二次函数y=x2-kx-2+k与轴两个交点为A、B,设此抛物线与y轴的交点为C,当k为6时,求S△ABC .2、已知抛物线y=x2+2x+m+1。
(1)若抛物线与x轴只有一个交点,求m的值。
(2)若抛物线与直线y=x+2m只有一个交点,求m的值。
3、已知抛物线y=x2-(m2+8)x+2(m2+6).
求证:不任m为何实数,抛物线与x轴都有两个不同的交点,4、已知抛物线C经过(-5,0)(0,5/2)(1,6)三点,直线L的解析式是Y=2X-3.
(1)求抛物线C的解析
(2)求证:抛物线C与直线L无交点
(3)若与L平行的直线Y=2x+m与抛物线C只有一个公共点P,求点P的坐标。四、小结1、若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A(x1,0 ), B( x2,0 )
2、若一元二次方程ax2+bx+c=0与二次三项式ax2+bx+c及二次函数y=ax2+bx+c这三个“二次”之间互相转化的关系。体现了数形结合的思想。
与
一元二次方程的关系平泉四中 毛艳玲一、探究探究1、求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标。解:∵A、B在轴上,
∴它们的纵坐标为0,
∴令y=0,则x2-3x+2=0
解得:x1=1,x2=2;
∴A(1,0) , B(2,0)你发现方程 的解x1、x2与A、B的坐标有什么联系?
x2-3x+2=0结论1:方程x2-3x+2=0的解就是抛物线y=x2-3x+2与x轴的两个交点的横坐标。因此,抛物线与一元二次方程是有密切联系的。即:若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与轴的两个交点坐标分别是A( ), B( )x1,0x2,0x探究2、抛物线与X 轴的交点个数能不能用一元二次方程的知识来说明呢?b2-4ac>0b2-4ac=0
b2-4ac<0OXY结论2:抛物线y=ax2+bx+c抛物线y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况说明: 1、 b2-4ac >0 一元二次方程ax2+bx+c=0
有两个不等的实数根与x轴有两个交点——相交。抛物线y=ax2+bx+c 2、 b2-4ac =0 一元二次方程ax2+bx+c=0
有两个相等的实数根与x轴有唯一公共点——相切(顶点)。抛物线y=ax2+bx+c 3、 b2-4ac <0 一元二次方程ax2+bx+c=0
没有实数根与x轴没有公共点——相离。二、基础训练1、已知抛物线y=x2-6x+a的顶点在x轴上,则a= ;若抛物线与x轴有两个交点,则a的范围是 ;
3、已知抛物线y=x2+px+q与x轴的两个交点为(-2,0),(3,0),则p= ,q= 。2、已知抛物线y=x2-3x+a+1与x轴最多只有一个交点,则a的范围是 。4、判断下列各抛物线是否与x轴相交,如果相交,求出交点的坐标。
(1)y=6x2-2x+1 (2)y=-15x2+14x+8
(3)y=x2-4x+46、抛物线y=ax2+bx+c(a≠0)的图象全部在轴下方的条件是( )
(A)a<0 b2-4ac≤0
(B)a<0 b2-4ac>0
(C)a>0 b2-4ac>0
(D)a<0 b2-4ac<0
D三、例题推荐1、已知二次函数y=x2-kx-2+k.
(1)求证:不论k取何值时,这个二次函数
y=x2-kx-2+k与x轴有两个不同的交点。
(2)如果二次函数y=x2-kx-2+k与轴两个交点为A、B,设此抛物线与y轴的交点为C,当k为6时,求S△ABC .2、已知抛物线y=x2+2x+m+1。
(1)若抛物线与x轴只有一个交点,求m的值。
(2)若抛物线与直线y=x+2m只有一个交点,求m的值。
3、已知抛物线y=x2-(m2+8)x+2(m2+6).
求证:不任m为何实数,抛物线与x轴都有两个不同的交点,4、已知抛物线C经过(-5,0)(0,5/2)(1,6)三点,直线L的解析式是Y=2X-3.
(1)求抛物线C的解析
(2)求证:抛物线C与直线L无交点
(3)若与L平行的直线Y=2x+m与抛物线C只有一个公共点P,求点P的坐标。四、小结1、若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A(x1,0 ), B( x2,0 )
2、若一元二次方程ax2+bx+c=0与二次三项式ax2+bx+c及二次函数y=ax2+bx+c这三个“二次”之间互相转化的关系。体现了数形结合的思想。
同课章节目录
