河北省平泉县第四中学人教版九年级数学上册课件:24.2.2直线和圆的位置关系(共29张PPT)
文档属性
| 名称 | 河北省平泉县第四中学人教版九年级数学上册课件:24.2.2直线和圆的位置关系(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-06 17:05:59 | ||
图片预览


文档简介
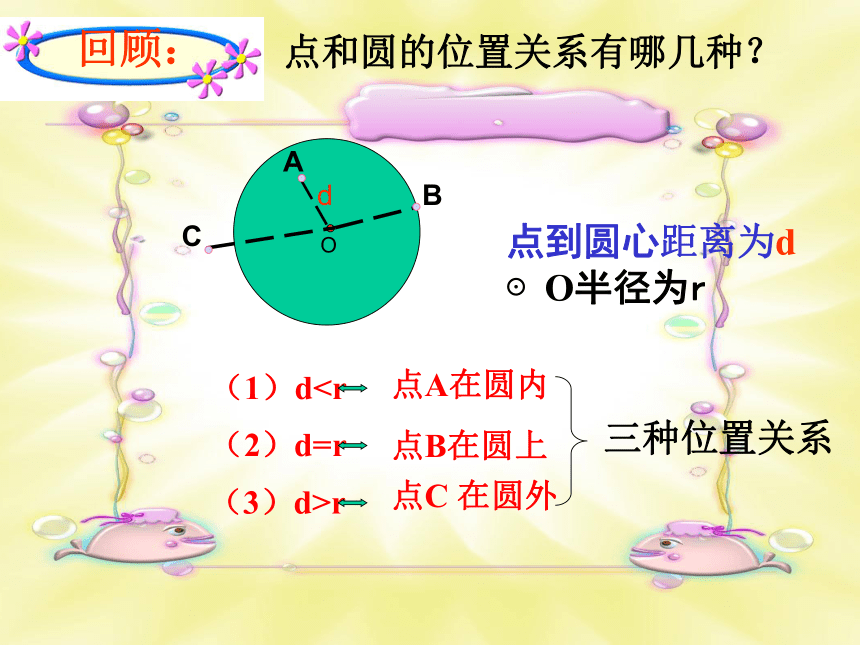
课件29张PPT。24.2.2直线与圆的位置关系河北省承德市平泉四海中学数学学科李淑敏点和圆的位置关系有哪几种?ABCd点A在圆内 点B在圆上点C 在圆外O点到圆心距离为d
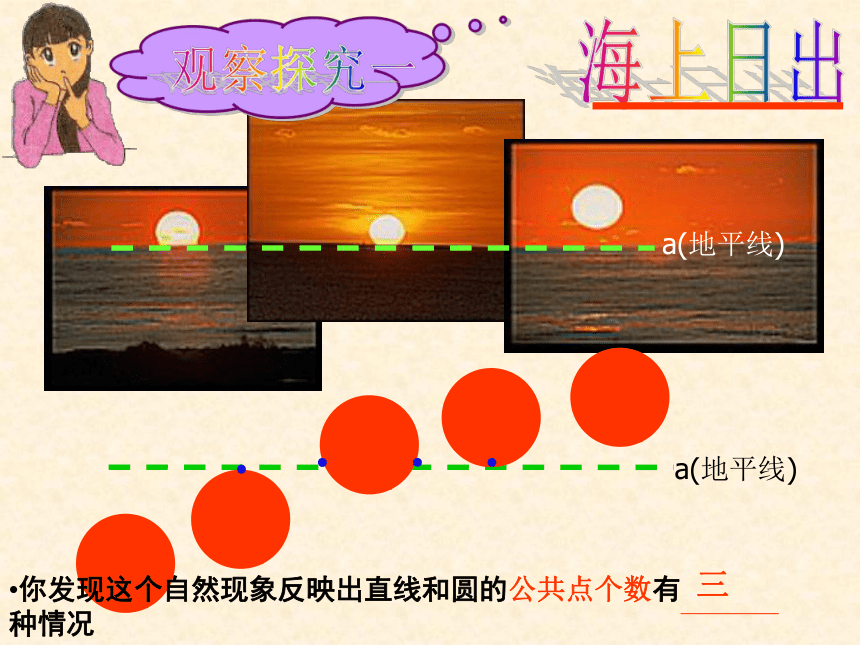
⊙O半径为r回顾: 把太阳看成一个圆,地平线看成一条直线,注意观察直线与圆的公共点的个数a(地平线)三海上日出观察探究一●●把钥匙环看作一个圆,把直尺边缘看成一条直线.
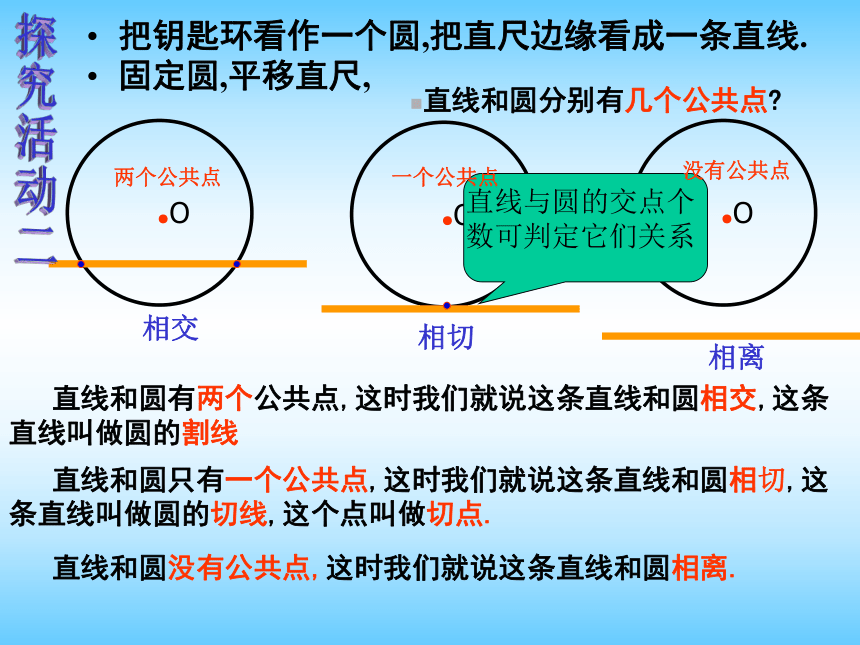
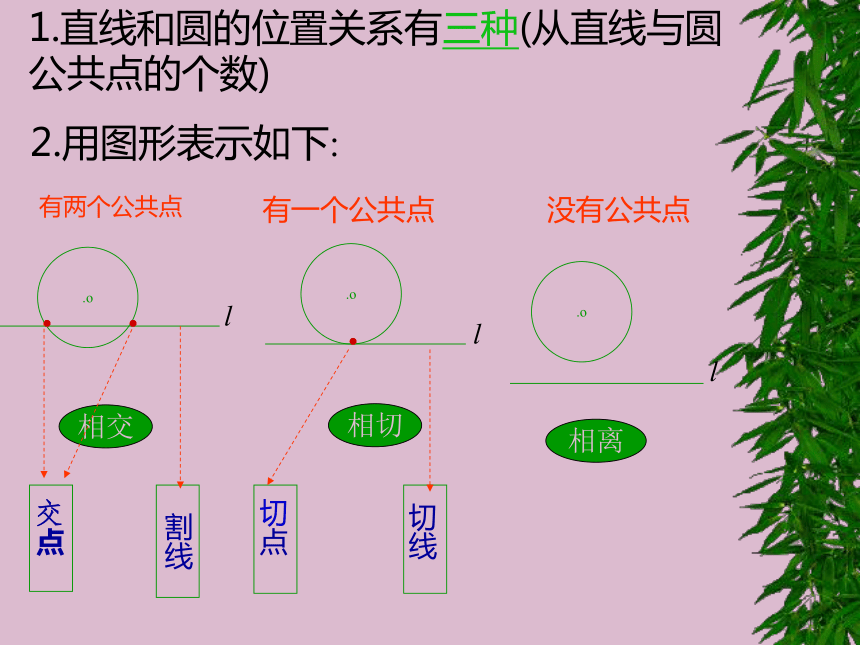
固定圆,平移直尺,直线和圆分别有几个公共点?相交相切相离探究活动二两个公共点没有公共点一个公共点·O·O·O·O看图判断直线l和 ⊙O的位置关系运用1.直线和圆的位置关系有三种(从直线与圆
公共点的个数)2.用图形表示如下:.o.o相切相交.没有公共点有一个公共点有两个公共点.ol
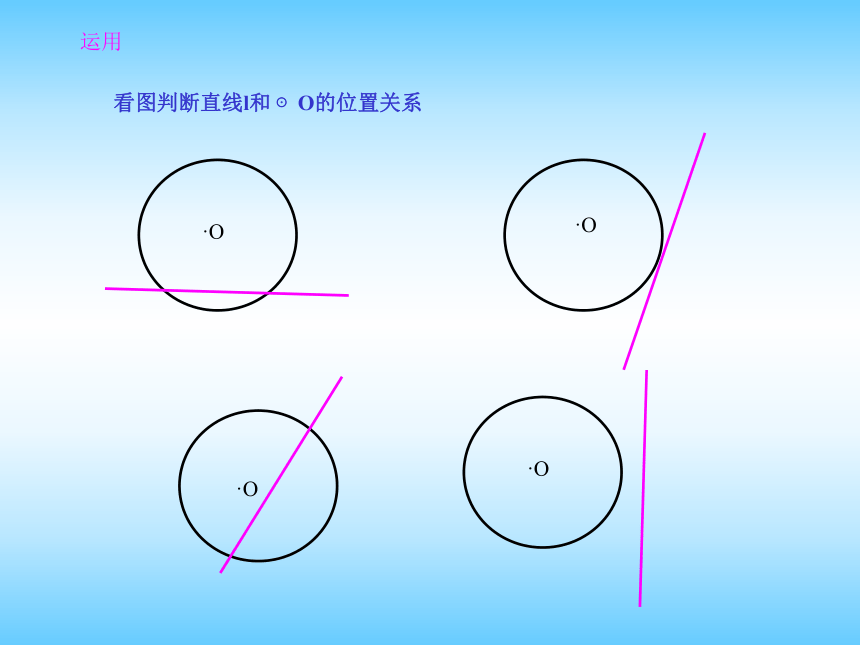
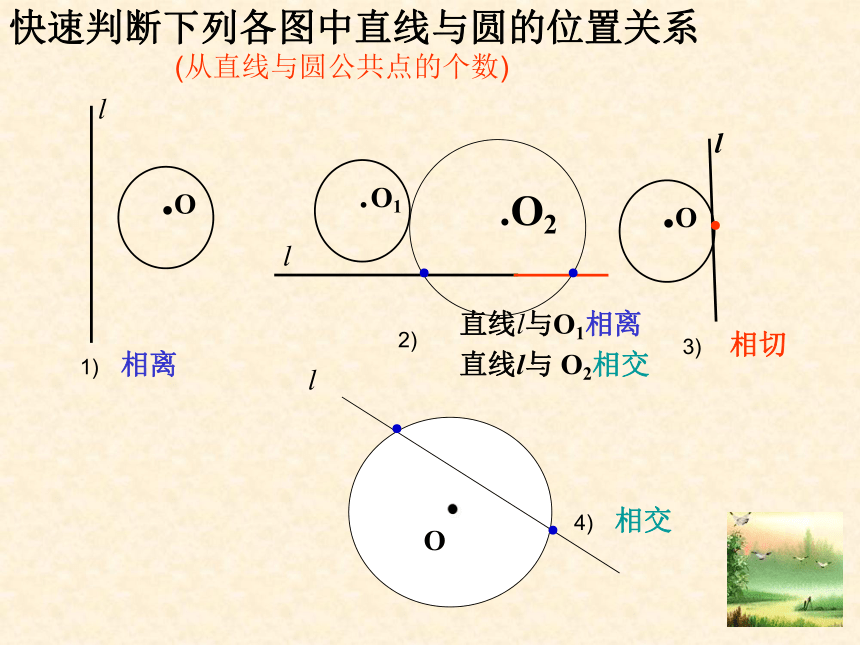
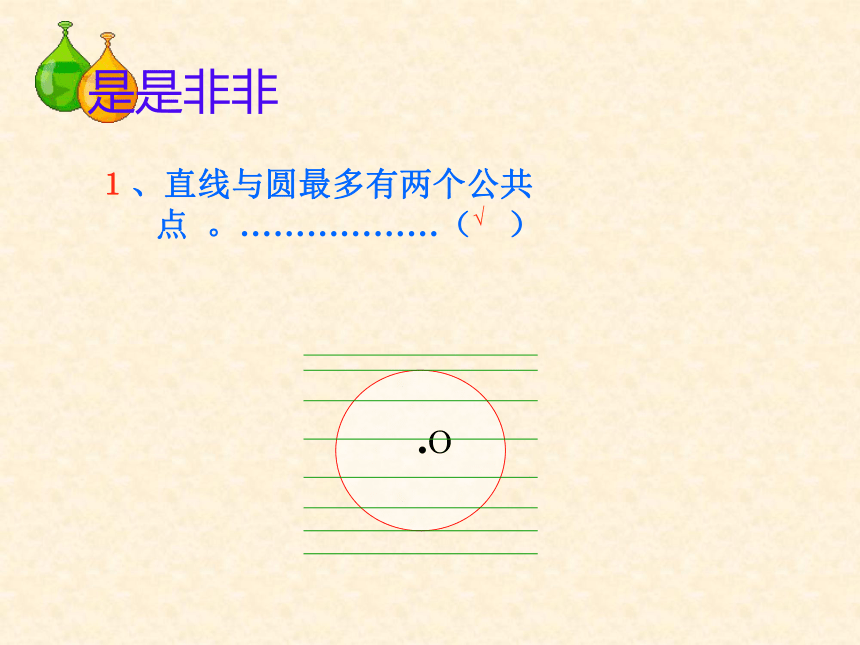
相离快速判断下列各图中直线与圆的位置关系ll.O2ll.1)2)3)4)相交相切相离直线l与O1相离直线l与 O2相交O(从直线与圆公共点的个数)●●●●●是是非非 1、直线与圆最多有两个公共
点 。………………( ) √是是非非×.C2、若C为⊙O上的一点,则过点C的直线与⊙O相切。… … … …( )是是非非3 、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )×是是非非√4、若C为⊙O内一点,则过点C的直线与⊙O相交。( )练 习 (一)填空:1、已知⊙O的半径为5cm,点O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点个数是____。
2、已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 ___ _。直线a与⊙O的公共点个数是____动动脑筋相交 相切21 3 已知⊙O的直径是6cm,O到直a的距离是4cm,则⊙O与直线a的位置关系是_____.相离练习(二):1、设⊙O的半径为4,点O到直线a的距离为d,
若⊙O与直线a至多只有一个公共点,则d为…( )
A、d≤4 B、d<4 C、d≥4 D、d=42、设⊙p的半径为4cm,直线l上一点A到圆心的
距离为4cm,则直线l与⊙O的位置关系
是……………………………………………( )
A、相交 B、相切 C、相离 D、相切或相交CD 过直线外一点作这条直线的垂线段,
垂线段的长度叫点到直线 的距离。课本102面第1题过A点近似地画⊙O的切线画一画:●如图,圆心O到直线的距离d与⊙O的半径r的大小有什么关系? 直线与圆的位置关系量化1)直线和圆相交d r;d r;2) 直线和圆相切3) 直线和圆相离d r;<=>1)直线和圆相交d r;d r;2) 直线和圆相切3) 直线和圆相离d r;直线与圆的位置关系量化<=>你能根据d与r的大小关系确定直线与圆的位置关系吗?过圆心作直线的垂线段 一判定直线 与圆的位置关系的方法有____种:(1)根据定义,由________________
的个数来判断;(2)由_________________ 的大小关系来判断。在实际应用中,常采用第二种方法判定。两直线 与圆的公共点圆心到直线的距离d与半径r
归纳:d > 6cmd = 6cmd < 6cm0cm≤2.直线和圆有2个交点,则直线和圆_________;
直线和圆有1个交点,则直线和圆_________;
直线和圆有没有交点,则直线和圆_________;
相交相切相离三、练习与例题 如图:∠AOB = 30°M是OB上的一点,且OM =5 cm 以M为圆心,以r 为半径的圆与 直线OA 有怎样的关系?为什么? (1)r = 2 cm ; (2) r = 4 cm ; (3) r = 2.5 cm .530° 解: 过 M 作 MC⊥OA 于 C,在 Rt △OMC 中, ∠AOB = 30°即圆心 M 到OA的距离 d = 2.5 cm.因此⊙M 和 直线OA 相离. (3) 当 r = 2.5cm 时,因此⊙M 和直线 OA 相切. (1) 当 r = 2 cm 时,(2) 当 r = 4 cm 时,因此⊙M 和直线O A 相交. 2.5有 d > r,有 d < r,有 d = r ,典型例题 如图:M是OB上的一点,且OM =5 cm 以M为圆心,半径r=2.5cm作⊙M. 试问过O的射线 OA与OB所夹的锐角a取什么值时射线OA与 ⊙M 1)相离 (2)相切 (3)相交 ?5a2.5例题的变式题 解: 过 M 作 MC⊥OA 于 C1)当∠a = 30°时,d=CM=2.5=r此时射线OA与 ⊙M相切 2)当 30°<∠a 时射线OA与⊙M相离3)当∠a <30°时射线OA与⊙M相交 < 90°2:圆的直径是13cm ,如果直线与圆心的距离分别是,
(1) 4.5cm ; (2) 6.5cm ; (3) 8cm.
那么直线和圆分别是什么位置关系?有几个公共点?
课本102面(3) 当 d = 8cm时, 有 d > r,因此圆与直线相离,没有公共点
当 r = 6.5cm时, 有 d = r,因此圆与直线相切,
有一个公共点当 d = 4.5cm时, 有 d < r, 因此圆与直线相交,
有两个公共点解: r=6.5cm,设直线与圆心的距离为d 设⊙O的圆心O到直线的距离为d,半径为r,d.r是
方程(m+9)x2- (m+6) x +1=0的两根,且直线与⊙O相切
时,求m的值?方程 几何综合练习题d=r析:直线与⊙O相切b2-4ac=0[-(m+6)]2-4(m+9)=0解得 m1= -8 m2= 0当m=-8时原方程 为x2+ 2x+1=0x1=x2= -1当m=0时原方程 为9x2- 6x+1=0(不符合题意舍去)d <rd =rd >r共同回顾两个唯一切线
切点没有割线
圆心O到直线的距离为d 直线和圆的位置关系有三种 如图:AB=8是大圆⊙O的弦,大圆半径为R=5,则以O为圆心,半径为3的小圆与A B的位置关系是( )补充练习A相离 B相切 C相交 D都有可能OAB543B8讨论:在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。1、当r满足________________时,⊙C与直线AB相离。2、当r满足____________ 时,⊙C与直线AB相切。3、当r满足____________时,
⊙C与直线AB相交。BCAD45d=2.4cm30cmAC=3cm,BC=4cm,
以C为圆心,r为半径作圆。想一想? 当r满足___________
_____________ 时,⊙C与线段AB只有一个公共点. r=2.4cmBCAD453d=2.4cm 或3cm2、识别直线与圆的位置关系的方法:
(1)一种是根据定义进行识别:
直线L和⊙o没有公共点 直线L与⊙o相离。
直线L和⊙o只有一个公共点 直线L与⊙o相切。
直线L和⊙o有两个公共点 直线L与⊙o相交。
(2)另一种是根据圆心到直线的距离d与圆的半径r之间
的数量关系来进行识别:
d>r 直线L与⊙o相离;
d=r 直线L与⊙o相切;
d1、直线和圆的位置关系有3种:相离、相切和相交。知识梳理作业:课本第94页第1、2题(四)课后作业布置谢谢观赏
再见!
⊙O半径为r回顾: 把太阳看成一个圆,地平线看成一条直线,注意观察直线与圆的公共点的个数a(地平线)三海上日出观察探究一●●把钥匙环看作一个圆,把直尺边缘看成一条直线.
固定圆,平移直尺,直线和圆分别有几个公共点?相交相切相离探究活动二两个公共点没有公共点一个公共点·O·O·O·O看图判断直线l和 ⊙O的位置关系运用1.直线和圆的位置关系有三种(从直线与圆
公共点的个数)2.用图形表示如下:.o.o相切相交.没有公共点有一个公共点有两个公共点.ol
相离快速判断下列各图中直线与圆的位置关系ll.O2ll.1)2)3)4)相交相切相离直线l与O1相离直线l与 O2相交O(从直线与圆公共点的个数)●●●●●是是非非 1、直线与圆最多有两个公共
点 。………………( ) √是是非非×.C2、若C为⊙O上的一点,则过点C的直线与⊙O相切。… … … …( )是是非非3 、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )×是是非非√4、若C为⊙O内一点,则过点C的直线与⊙O相交。( )练 习 (一)填空:1、已知⊙O的半径为5cm,点O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点个数是____。
2、已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 ___ _。直线a与⊙O的公共点个数是____动动脑筋相交 相切21 3 已知⊙O的直径是6cm,O到直a的距离是4cm,则⊙O与直线a的位置关系是_____.相离练习(二):1、设⊙O的半径为4,点O到直线a的距离为d,
若⊙O与直线a至多只有一个公共点,则d为…( )
A、d≤4 B、d<4 C、d≥4 D、d=42、设⊙p的半径为4cm,直线l上一点A到圆心的
距离为4cm,则直线l与⊙O的位置关系
是……………………………………………( )
A、相交 B、相切 C、相离 D、相切或相交CD 过直线外一点作这条直线的垂线段,
垂线段的长度叫点到直线 的距离。课本102面第1题过A点近似地画⊙O的切线画一画:●如图,圆心O到直线的距离d与⊙O的半径r的大小有什么关系? 直线与圆的位置关系量化1)直线和圆相交d r;d r;2) 直线和圆相切3) 直线和圆相离d r;<=>1)直线和圆相交d r;d r;2) 直线和圆相切3) 直线和圆相离d r;直线与圆的位置关系量化<=>你能根据d与r的大小关系确定直线与圆的位置关系吗?过圆心作直线的垂线段 一判定直线 与圆的位置关系的方法有____种:(1)根据定义,由________________
的个数来判断;(2)由_________________ 的大小关系来判断。在实际应用中,常采用第二种方法判定。两直线 与圆的公共点圆心到直线的距离d与半径r
归纳:d > 6cmd = 6cmd < 6cm0cm≤2.直线和圆有2个交点,则直线和圆_________;
直线和圆有1个交点,则直线和圆_________;
直线和圆有没有交点,则直线和圆_________;
相交相切相离三、练习与例题 如图:∠AOB = 30°M是OB上的一点,且OM =5 cm 以M为圆心,以r 为半径的圆与 直线OA 有怎样的关系?为什么? (1)r = 2 cm ; (2) r = 4 cm ; (3) r = 2.5 cm .530° 解: 过 M 作 MC⊥OA 于 C,在 Rt △OMC 中, ∠AOB = 30°即圆心 M 到OA的距离 d = 2.5 cm.因此⊙M 和 直线OA 相离. (3) 当 r = 2.5cm 时,因此⊙M 和直线 OA 相切. (1) 当 r = 2 cm 时,(2) 当 r = 4 cm 时,因此⊙M 和直线O A 相交. 2.5有 d > r,有 d < r,有 d = r ,典型例题 如图:M是OB上的一点,且OM =5 cm 以M为圆心,半径r=2.5cm作⊙M. 试问过O的射线 OA与OB所夹的锐角a取什么值时射线OA与 ⊙M 1)相离 (2)相切 (3)相交 ?5a2.5例题的变式题 解: 过 M 作 MC⊥OA 于 C1)当∠a = 30°时,d=CM=2.5=r此时射线OA与 ⊙M相切 2)当 30°<∠a 时射线OA与⊙M相离3)当∠a <30°时射线OA与⊙M相交 < 90°2:圆的直径是13cm ,如果直线与圆心的距离分别是,
(1) 4.5cm ; (2) 6.5cm ; (3) 8cm.
那么直线和圆分别是什么位置关系?有几个公共点?
课本102面(3) 当 d = 8cm时, 有 d > r,因此圆与直线相离,没有公共点
当 r = 6.5cm时, 有 d = r,因此圆与直线相切,
有一个公共点当 d = 4.5cm时, 有 d < r, 因此圆与直线相交,
有两个公共点解: r=6.5cm,设直线与圆心的距离为d 设⊙O的圆心O到直线的距离为d,半径为r,d.r是
方程(m+9)x2- (m+6) x +1=0的两根,且直线与⊙O相切
时,求m的值?方程 几何综合练习题d=r析:直线与⊙O相切b2-4ac=0[-(m+6)]2-4(m+9)=0解得 m1= -8 m2= 0当m=-8时原方程 为x2+ 2x+1=0x1=x2= -1当m=0时原方程 为9x2- 6x+1=0(不符合题意舍去)d <rd =rd >r共同回顾两个唯一切线
切点没有割线
圆心O到直线的距离为d 直线和圆的位置关系有三种 如图:AB=8是大圆⊙O的弦,大圆半径为R=5,则以O为圆心,半径为3的小圆与A B的位置关系是( )补充练习A相离 B相切 C相交 D都有可能OAB543B8讨论:在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。1、当r满足________________时,⊙C与直线AB相离。2、当r满足____________ 时,⊙C与直线AB相切。3、当r满足____________时,
⊙C与直线AB相交。BCAD45d=2.4cm30cm
以C为圆心,r为半径作圆。想一想? 当r满足___________
_____________ 时,⊙C与线段AB只有一个公共点. r=2.4cmBCAD453d=2.4cm 或3cm
(1)一种是根据定义进行识别:
直线L和⊙o没有公共点 直线L与⊙o相离。
直线L和⊙o只有一个公共点 直线L与⊙o相切。
直线L和⊙o有两个公共点 直线L与⊙o相交。
(2)另一种是根据圆心到直线的距离d与圆的半径r之间
的数量关系来进行识别:
d>r 直线L与⊙o相离;
d=r 直线L与⊙o相切;
d
再见!
同课章节目录
